Gleichungen¶
Lineare Gleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Lineare Gleichungen.
Zur Lösung der Gleichung empfiehlt es sich, beide Seiten der Gleichung mit dem Hauptnenner
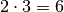 der auftretenden Terme zu multiplizieren.
der auftretenden Terme zu multiplizieren.![\frac{10 \cdot x+3}{3} -5 &= 11 - \frac{3 \cdot x + 4}{2} - \frac{2 \cdot x
+6}{3} \\[4pt]
6 \cdot \left( \frac{10 \cdot x+3}{3} -5 \right) &= 6 \cdot \left( 11 -
\frac{3 \cdot x + 4}{2} - \frac{2 \cdot x +6}{3} \right) \\[4pt]](../../_images/math/d5dd10eeb98e27ac24aa0648888dcb2667d8d874.png)
Multipliziert man die Klammern aus, so können die auftretenden Brüche durch Kürzen beseitigt werden. Man erhält dadurch:
![{\color{white}....}2 \cdot (10 \cdot x+3) \; - \; 30 = 66 - 3 \cdot (3
\cdot x + 4) - 2 \cdot (2 \cdot x +6) \\[4pt]](../../_images/math/009f5b0e8936d98dd35fa5928bb42c82d395e80a.png)
Die Gleichung kann durch ein Ausmultiplizieren der Klammern weiter vereinfacht werden:
![20 \cdot x+6 \; - \; 30 = 66 - 9 \cdot x - 12 - 4 \cdot x - 12 \\[4pt]](../../_images/math/19fa555e04fa617d87336e01d90f64249d7455da.png)
Zum Auflösen werden alle
 -Terme auf eine Seite der Gleichung, alle
anderen Terme auf die andere Seite der Gleichung gebracht. Damit folgt:
-Terme auf eine Seite der Gleichung, alle
anderen Terme auf die andere Seite der Gleichung gebracht. Damit folgt: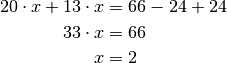
Die Lösung der Gleichung lautet somit
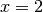 .
.
Quadratische Gleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Quadratische Gleichungen.
 Die Lösungsformel für quadratische Gleichungen
(„Mitternachtsformel“) liefert für die gegebene Gleichung
Die Lösungsformel für quadratische Gleichungen
(„Mitternachtsformel“) liefert für die gegebene Gleichung 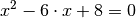 mit
mit 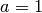 ,
, 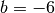 und
und 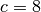 :
: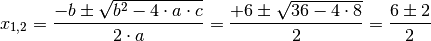
Somit ergeben sich folgende Lösungen:
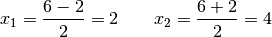
Die Lösungsmenge der Gleichung lautet somit
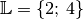 .
.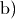 Zum Lösen der Gleichung
Zum Lösen der Gleichung 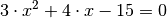 sind in die „Mitternachtsformel“ die Werte
sind in die „Mitternachtsformel“ die Werte 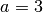 ,
, 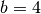 und
und
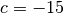 einzusetzen. Man erhält damit:
einzusetzen. Man erhält damit: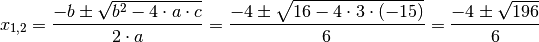
Die Wurzel
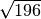 ergibt den Wert
ergibt den Wert 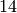 . Als Lösungen erhält
man damit:
. Als Lösungen erhält
man damit: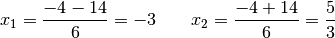
Die Lösungsmenge der Gleichung lautet somit
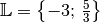 .
.
Der Satz von Vieta ist insbesondere dann nützlich, wenn eine quadratische Gleichung der Form
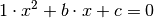 vorliegt und
vorliegt und
 sowie
sowie  ganze Zahlen sind.
ganze Zahlen sind.Man prüft dann als erstes, durch welche Produkt zweier Zahlen sich die Zahl
 darstellen lässt. Im Fall
darstellen lässt. Im Fall 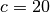 ergeben sich folgende
Möglichkeiten:
ergeben sich folgende
Möglichkeiten: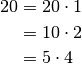
Ebenfalls möglich sind die Produkte
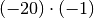 ,
, 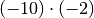 und
und 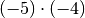 . Eine dieser drei beziehungsweise
sechs Möglichkeiten gibt die beiden Lösungen der Gleichung an.
. Eine dieser drei beziehungsweise
sechs Möglichkeiten gibt die beiden Lösungen der Gleichung an.Um zu prüfen, welche der obigen Möglichkeiten die Gleichung löst, bildet man die Summen der einzelnen Wertepaare:
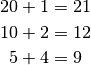
Das „richtige“ Wertepaar erkennt man daran, dass die Summe einen Wert ergibt, der mit dem Wert von
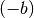 identisch ist. In dieser Aufgabe ist
identisch ist. In dieser Aufgabe ist
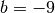 , also ist
, also ist 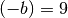 . Die Lösung der Gleichung lautet
somit:
. Die Lösung der Gleichung lautet
somit: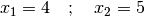
Als Produktform lässt sich die Gleichung damit wie folgt schreiben:
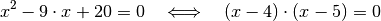
Algebraische Gleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Algebraische Gleichungen höheren Grades.
Existiert die Lösung
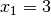 , so kann der Gleichungsterm in ein Produkt
aus dem Linearfaktor
, so kann der Gleichungsterm in ein Produkt
aus dem Linearfaktor 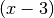 und einem Restterm zerlegt werden. Dieser
kann mittels einer Polynom-Division ermittelt werden; es muss also folgende
Rechnung durchgeführt werden:
und einem Restterm zerlegt werden. Dieser
kann mittels einer Polynom-Division ermittelt werden; es muss also folgende
Rechnung durchgeführt werden: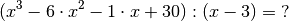
Als erstes prüft man, mit welchem Faktor
 zu multiplizieren ist, um
zu multiplizieren ist, um
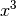 zu erhalten; als Ergebnis kann man
zu erhalten; als Ergebnis kann man 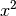 auf die rechte
Seite schreiben. Das Produkt aus
auf die rechte
Seite schreiben. Das Produkt aus 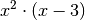 muss dann vom
ursprünglichen Term abgezogen werden. Man erhält:
muss dann vom
ursprünglichen Term abgezogen werden. Man erhält:![\begin{array}{rlll}
(x^3 &- 6 \cdot x^2 &- 1 \cdot x &+ 30) : (x - 3) = x^2 \; + \; ?\\
-(x^3 & - 3 \cdot x^2) \\ \cline{1-2} \\[-8pt]
& -3 \cdot x^2 & - 1\cdot x &+ 30 \\
\end{array}](../../_images/math/966a7cae7e9329a135c4c4cf73a1a848b526a20e.png)
Als nächstes ist also zu prüfen, mit welchem Faktor
 zu
multiplizieren ist, um
zu
multiplizieren ist, um 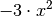 zu erhalten; als Ergebnis kann man
wiederum
zu erhalten; als Ergebnis kann man
wiederum 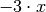 auf die rechte Seite schreiben. Das Produkt aus
auf die rechte Seite schreiben. Das Produkt aus
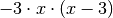 muss vom verbleibenden Term abgezogen werden.
Man erhält:
muss vom verbleibenden Term abgezogen werden.
Man erhält:![\begin{array}{rlll}
(x^3 &- 6 \cdot x^2 &- 1 \cdot x &+ 30) : (x - 3) = x^2 - 3 \cdot x \;
+ \; ?\\
-(x^3 & - 3 \cdot x^2) \\ \cline{1-2} \\[-8pt]
& -3 \cdot x^2 & - 1 \cdot x &+ 30 \\
\qquad -(& -3 \cdot x^2 & + 9 \cdot x) \\\cline{1-3}\\[-8pt]
&& -10 \cdot x & + 30
\end{array}](../../_images/math/53e6f2e77dbc80f7d2276dec8617b7371ce78096.png)
Um den verbleibenden Term zu erhalten, muss
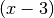 mit dem Faktor
mit dem Faktor
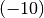 multipliziert werden. Man erhält also:
multipliziert werden. Man erhält also:![\begin{array}{rllll}
(x^3 &- 6 \cdot x^2 &- 1 \cdot x &+ 30) & : (x - 3) = x^2 - 3 \cdot x - 10\\
-(x^3 & - 3 \cdot x^2) \\ \cline{1-2} \\[-8pt]
& -3 \cdot x^2 & - 1 \cdot x &+ 30 \\
\qquad -(& -3 \cdot x^2 & + 9 \cdot x) \\\cline{1-3}\\[-8pt]
&&-10 \cdot x & + 30 \\
&\qquad -(&-10 \cdot x & + 30) \\\cline{1-4}\\[-8pt]
&&& 0
\end{array}](../../_images/math/296f575a3929b5d82ed97b7488cea6745cc318e1.png)
Der bei der Polynomdivision verbleibende Rest-Term ist also
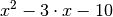 . Setzt man diesen Term gleich Null, so kann man die
verbleibenden Lösungen der ursprünglichen Gleichung berechnen:
. Setzt man diesen Term gleich Null, so kann man die
verbleibenden Lösungen der ursprünglichen Gleichung berechnen: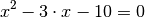
Diese quadratische Gleichung kann wahlweise mittels der Mitternachtsformel oder (in diesem Fall wohl einfacher) mittels des Satzes von Vieta gelöst werden. Man erhält:

Die Lösungsmenge der ursprünglichen Gleichung lautet somit
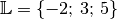 .
.
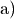 Die Gleichung
Die Gleichung 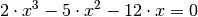 enthält auf der linken Gleichungs-Seite keinen Zahlenterm; es kann somit
enthält auf der linken Gleichungs-Seite keinen Zahlenterm; es kann somit
 ausgeklammert werden:
ausgeklammert werden:![2 \cdot x^3 - 5 \cdot x^2 - 12 \cdot x &= 0 \\[4pt]
\Rightarrow x \cdot (2 \cdot x^2 - 5 \cdot x - 12) &= 0 \\[4pt]](../../_images/math/de20a37aeb3e749c020cf491054c4e4c901536a1.png)
Man erhält damit unmittelbar
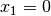 als erste Lösung der Gleichung. Die
übrigen Lösungen erhält man, wenn man den Restterm gleich Null setzt (denn ein
Produkt ist stets dann Null, wenn einer der Faktoren gleich Null ist):
als erste Lösung der Gleichung. Die
übrigen Lösungen erhält man, wenn man den Restterm gleich Null setzt (denn ein
Produkt ist stets dann Null, wenn einer der Faktoren gleich Null ist):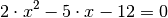
Mittels der „Mitternachtsformel“ erhält man mit
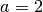 ,
, 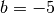 und
und
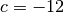 :
: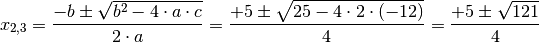
Die Wurzel
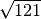 ergibt den Wert
ergibt den Wert 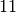 . Als Lösungen erhält
man damit:
. Als Lösungen erhält
man damit: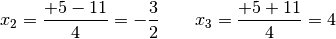
Die Lösungsmenge der Gleichung lautet also
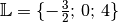 .
.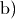 Die Gleichung
Die Gleichung 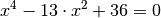 enthält
auf der linken Seite nur
enthält
auf der linken Seite nur  -Terme mit geraden Exponenten; man kann
daher
-Terme mit geraden Exponenten; man kann
daher 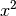 durch eine neue Variable
durch eine neue Variable  ersetzen
(„Substitution“). Für diese neue Variable ergibt sich folgende Gleichung:
ersetzen
(„Substitution“). Für diese neue Variable ergibt sich folgende Gleichung: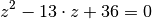
Diese quadratische Gleichung kann wahlweise mittels der Mitternachtsformel oder (in diesem Fall wohl einfacher) mittels des Satzes von Vieta gelöst werden. Man erhält:

Die ursprüngliche Gleichung hat höchstens vier Lösungen, da der größte auftretende Exponent gleich vier ist. Diese Lösungen ergeben sich mit den obigen Lösungen für
 folgendermaßen:
folgendermaßen: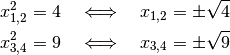
Man erhält damit als Lösungen
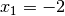 ,
, 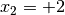 ,
, 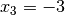 und
und 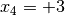 . Durch Einsetzen dieser Werte in die ursprüngliche
Gleichung kann/muss geprüft werden, ob es sich tatsächlich um Lösungen der
ursprünglichen Gleichung handelt, da durch das Quadrieren beziehungsweise
Wurzelziehen (keine Äquivalenzumformung!) „Scheinlösungen“ entstehen können.
. Durch Einsetzen dieser Werte in die ursprüngliche
Gleichung kann/muss geprüft werden, ob es sich tatsächlich um Lösungen der
ursprünglichen Gleichung handelt, da durch das Quadrieren beziehungsweise
Wurzelziehen (keine Äquivalenzumformung!) „Scheinlösungen“ entstehen können.Da die obigen Werte tatsächlich die Gleichung erfüllen, ergibt sich als Lösungsmenge der Gleichung
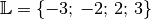 .
.
Bruch-, Produkt- und Wurzelgleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Bruch-, Produkt- und Wurzelgleichungen.
Bruch- und Produktgleichungen
Bei der Gleichung handelt es sich um eine Produkt-Gleichung; für den Definitionsbereich gilt
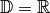 , es dürfen also alle
reellen Zahlen für
, es dürfen also alle
reellen Zahlen für  eingesetzt werden.
eingesetzt werden.Um die Gleichung zu lösen, ist es hilfreich, alle die Variable
 beinhaltende Terme auf die linke Seite zu sortieren. Dadurch erhält man:
beinhaltende Terme auf die linke Seite zu sortieren. Dadurch erhält man: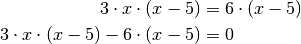
Auf der linken Seite kann nun der Term
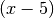 ausgeklammert werden.
Daraus ergibt sich:
ausgeklammert werden.
Daraus ergibt sich: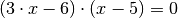
Ein Produkt hat genau dann den Wert Null, wenn einer der Faktoren Null ist. Die Gleichung ist somit in den folgenden beiden Fällen erfüllt:
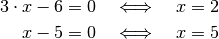
Die Lösungsmenge der Gleichung ist somit
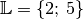 .
.Hinweis: Würde man im ersten Schritt durch
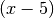 dividieren, so
bliebe nur noch die Lösung
dividieren, so
bliebe nur noch die Lösung 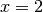 übrig. Bei einer Division einer
Gleichung durch einen Term muss also stets darauf geachtet werden, dass dieser
Term ungleich Null ist; gegebenenfalls muss eine Fallunterscheidung
vorgenommen und dieser Fall – im obigen Beispiel
übrig. Bei einer Division einer
Gleichung durch einen Term muss also stets darauf geachtet werden, dass dieser
Term ungleich Null ist; gegebenenfalls muss eine Fallunterscheidung
vorgenommen und dieser Fall – im obigen Beispiel 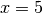 – separat
untersucht werden.
– separat
untersucht werden.
Bei Bruchgleichungen muss ausgeschlossen sein, dass die Nenner der auftretenden Terme gleich Null werden; es muss also gelten:
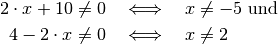
Um die Gleichung zu lösen, ist es empfehlenswert, beide Seiten der Gleichung mit dem Hauptnenner
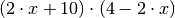 zu
multiplizieren. Nach dem Kürzen entfallen dadurch die Nenner:
zu
multiplizieren. Nach dem Kürzen entfallen dadurch die Nenner:![\frac{3 \cdot x + 13}{2 \cdot x + 10} &= \frac{4 - 3 \cdot x}{4 - 2\cdot
x} \\[8pt]
\frac{\cancel{(2 \cdot x + 10)} \cdot (4 - 2 \cdot x) \cdot (3 \cdot x +
13)}{\cancel{2 \cdot x + 10}} &= \frac{(4 - 3 \cdot x) \cdot (2 \cdot x +
10) \cdot \cancel{(4 - 2 \cdot x)}}{\cancel{4 - 2\cdot x}} \\[8pt]
\Rightarrow (4 - 2 \cdot x) \cdot (3 \cdot x + 13) &= (4 - 3 \cdot x)
\cdot (2 \cdot x + 10)](../../_images/math/7d524c0d7ef26f6440ffedf06f35954f4cf7d1d4.png)
Um diese Gleichung weiter zu vereinfachen, müssen die Terme auf beiden Seiten ausmultipliziert werden, denn ansonsten wäre ein Sortieren der Gleichung in Variablen-Terme und reine Zahlen-Terme nicht möglich. Man erhält:
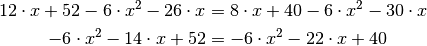
Sortiert man nun alle
 -Terme auf die linke und alle übrigen Terme auf
die rechte Seite, so entfällt der quadratische Term. Übrig bleibt eine lineare
Gleichung mit folgender Lösung:
-Terme auf die linke und alle übrigen Terme auf
die rechte Seite, so entfällt der quadratische Term. Übrig bleibt eine lineare
Gleichung mit folgender Lösung: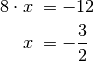
Die Lösungsmenge der Gleichung ist somit
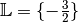 .
.
Wurzelgleichungen
Betrachtet man (ohne jegliche algebraische Umformung) den Definitionsbereich der Gleichung, so stellt man fest, dass dieser der leeren Menge
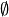 entspricht: Es gibt nämlich keinen Wert für die Variable
entspricht: Es gibt nämlich keinen Wert für die Variable
 , so dass die beiden Bedingungen
, so dass die beiden Bedingungen 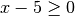 und
und 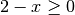 gleichzeitig erfüllt sind. Da dies nicht möglich ist, kann die Gleichung
folglich für keine reelle Zahl
gleichzeitig erfüllt sind. Da dies nicht möglich ist, kann die Gleichung
folglich für keine reelle Zahl 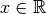 erfüllt werden.
erfüllt werden.
 Die Definitionsmenge ergibt sich, da reellwertige Wurzeln
nicht negativ sein dürfen, aus folgenden Ungleichungen:
Die Definitionsmenge ergibt sich, da reellwertige Wurzeln
nicht negativ sein dürfen, aus folgenden Ungleichungen: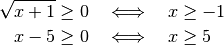
Da beide Bedingungen zugleich gelten müssen und die zweite Bedingung
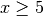 die erste Bedingung
die erste Bedingung  hinreichend mit einschließt, gilt
für den Definitionsbereich der Gleichung
hinreichend mit einschließt, gilt
für den Definitionsbereich der Gleichung 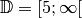 .
.Um die Gleichung zu lösen, können die Terme auf beiden Seiten in einem ersten Rechenschritt quadriert werden. Man erhält hierbei:
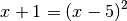
Diese Gleichung entspricht nun einer quadratischen Gleichung. Um sie zu lösen, werden alle Terme auf die linke Seite sortiert und anschließend Klammer der quadratische Term
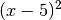 ausgewertet:
ausgewertet: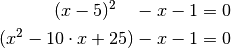
Da in der resultierenden Gleichung alle Operatoren die gleiche Priorität haben und vor der Klammer kein Minuszeichen steht, können die Klammern weggelassen werden. Die
 -Terme sowie die Zahlenwerte können noch folgendermaßen
zusammengefasst werden:
-Terme sowie die Zahlenwerte können noch folgendermaßen
zusammengefasst werden: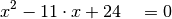
Diese Gleichung kann beispielsweise mit der Lösungsformel für quadratische Gleichungen gelöst werden. Mit
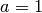 ,
, 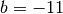 und
und 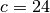 erhält man:
erhält man: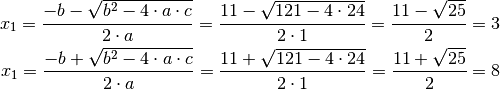
Man könnte nun annehmen, dass die Lösungsmenge gleich
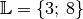 ist – doch das ist falsch! Die Definitionsmenge
ist – doch das ist falsch! Die Definitionsmenge 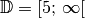 der ursprünglichen Gleichung schließt die Lösung
der ursprünglichen Gleichung schließt die Lösung 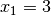 der späteren quadratischen Gleichung aus. Der Grund für das Hinzukommen der
„Scheinlösung“ liegt im ersten Rechenschritt, nämlich dem Quadrieren beider
Seiten der Gleichung. Da diese Umformung keine Äquivalenz-Umformung ist,
können – wie in diesem Beispiel – weitere Lösungen hinzukommen.
der späteren quadratischen Gleichung aus. Der Grund für das Hinzukommen der
„Scheinlösung“ liegt im ersten Rechenschritt, nämlich dem Quadrieren beider
Seiten der Gleichung. Da diese Umformung keine Äquivalenz-Umformung ist,
können – wie in diesem Beispiel – weitere Lösungen hinzukommen.Neben einem Blick auf den Definitionsbereich schließt auch ein Einsetzen der erhaltenen Lösungen in die ursprüngliche Gleichung die Scheinlösung
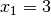 aus. Die Lösungsmenge lautet also
aus. Die Lösungsmenge lautet also 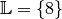 .
. Der Definitionsbereich dieser Gleichung muss folgende beide
Bedingungen erfüllen:
Der Definitionsbereich dieser Gleichung muss folgende beide
Bedingungen erfüllen:
Der Definitionsbereich
 der Gleichung entspricht somit dem
Intervall
der Gleichung entspricht somit dem
Intervall ![[-2\tfrac{1}{3};\; 1]](../../_images/math/53e8042a0bca9d96948523336a5df084a5998c13.png) . Durch ein Quadrieren der Gleichung
ergibt sich:
. Durch ein Quadrieren der Gleichung
ergibt sich:![\left( \sqrt{3 \cdot x + 7} \right)^2 = \left( 2 - 2 \cdot x \right)^2 \\[4pt]
3 \cdot x + 7 = 4 - 8 \cdot x + 4 \cdot x^2 \\[4pt]](../../_images/math/008c3acb3149cd07521d75732d80dfe645d753bb.png)
Durch das Quadrieren wird die Wurzelgleichung somit zu einer quadratischen Gleichung. Durch ein Sortieren der einzelnen Terme auf die linke Gleichungsseite kann diese auf Normalform gebracht werden:
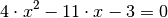
Mittels der „Mitternachtsformel“ kann diese Gleichung gelöst werden, wenn man für
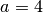 ,
, 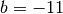 und
und 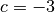 setzt:
setzt: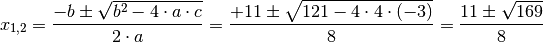
Die Wurzel
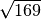 ergibt den Wert
ergibt den Wert 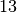 . Als Lösungen erhält
man damit:
. Als Lösungen erhält
man damit: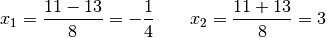
Nur die Lösung
 ist im Definitionsbereich
ist im Definitionsbereich 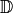 der
Gleichung enthalten,
der
Gleichung enthalten, 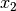 hingegen stellt eine durch das Quadrieren der
Gleichung entstandene Scheinlösung dar. Die Lösungsmenge der Gleichung lautet
somit
hingegen stellt eine durch das Quadrieren der
Gleichung entstandene Scheinlösung dar. Die Lösungsmenge der Gleichung lautet
somit 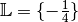 .
.
Exponential- und Logarithmusgleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Exponential- und Logarithmusgleichungen.
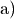 Die Gleichung kann gelöst werden, indem beide Seiten
logarithmiert werden:
Die Gleichung kann gelöst werden, indem beide Seiten
logarithmiert werden:![3^{x} &= 12 \\[4pt]
\Rightarrow \; \log{\left(3^{x}\right)} &= \log{(12)}](../../_images/math/06889e53bf2e5d764ba0b5630ed608598f4330ca.png)
Die Wahl des
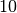 -er-Logarithmus war/ist hierbei willkürlich. Nun kann
allerdings die Rechenregel
-er-Logarithmus war/ist hierbei willkürlich. Nun kann
allerdings die Rechenregel 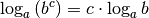 genutzt werden (siehe Rechenregeln für Logarithmen), so dass sich folgende Gleichung ergibt:
genutzt werden (siehe Rechenregeln für Logarithmen), so dass sich folgende Gleichung ergibt: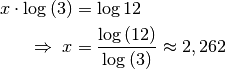
Die Gleichung gilt also für
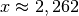 .
.
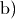 Die Gleichung kann gelöst werden, indem beide Seiten
auf die gleiche Basis gebracht werden. Auf der rechten Seite der Gleichung
nämlich
Die Gleichung kann gelöst werden, indem beide Seiten
auf die gleiche Basis gebracht werden. Auf der rechten Seite der Gleichung
nämlich 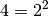 gesetzt werden:
gesetzt werden: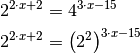
Diese Umformung hat den Vorteil, dass nun die Rechenregel
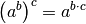 angewendet werden kann:
angewendet werden kann: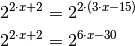
Sind die Basen auf beiden Seiten der Gleichung identisch, so müssen auch die Exponenten gleich sein. Es muss also gelten:
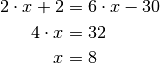
Die Gleichung hat somit die Lösung
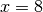 .
.
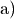 Die Definitionsmenge der Gleichung ist
Die Definitionsmenge der Gleichung ist 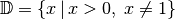 .
.Gemäß der Definition eines Logarithmus kann die Gleichung auch wie folgt geschrieben werden:
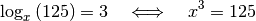
Zieht man bei der Gleichung auf der rechten Seite die dritte Wurzel, so erhält man:
![x = \sqrt[3]{125} = \pm 5](../../_images/math/abf4a0b8d2bd9a281b6d101b752ba20bc11da523.png)
Unter Berücksichtigung der Definitionsmenge lautet die Lösung somit
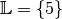 .
.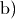 Um die Gleichung zu lösen, werden zunächst beide Seiten der
Gleichung als Exponenten zur Basis
Um die Gleichung zu lösen, werden zunächst beide Seiten der
Gleichung als Exponenten zur Basis 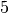 geschrieben. Auf der linken Seite
entfällt dabei wegen
geschrieben. Auf der linken Seite
entfällt dabei wegen 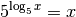 der Logarithmus:
der Logarithmus:![\log_{5}{(3 \cdot x - 2)} &= 4 \\[4pt]
\Rightarrow \; 3 \cdot x - 2 &= 5^4 \\
3 \cdot x - 2 &= 625 \\
3 \cdot x &= 627 \\
x &= 209](../../_images/math/d053ed6004f000aeb5ed0a7cf9a5cbbd88827b67.png)
Die Gleichung hat somit die Lösung
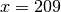 .
.
