Ungleichungen¶
Quadratische Ungleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Quadratische Ungleichungen.
Mittels des Satzes von Vieta kann man schnell ermitteln, dass die Gleichung
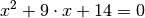 die Nullstellen
die Nullstellen 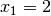 und
und
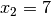 besitzt; man kann die Ungleichung also auch folgendermaßen
darstellen:
besitzt; man kann die Ungleichung also auch folgendermaßen
darstellen:![x^2 + 9 \cdot x + 14 &< 0 \\[4pt]
\Longleftrightarrow (x-2) \cdot (x-7) &< 0 \\[4pt]](../_images/math/03274b2d9a7c9429ccd4a8d237c87df2c5dd8390.png)
Die Ungleichung ist dann erfüllt, wenn einer der beiden Faktoren auf der linken Seite größer Null und der andere kleiner Null ist. Mit dieser Fallunterscheidung ergibt sich:
Für
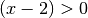 und
und 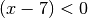 :
:![x - 2 > 0 \quad \text{ und } \quad x - 7 < 0 \\[4pt]
x > 2 \quad \text{ und } \quad x < 7 \\[4pt]](../_images/math/cbb8a40a181b875fa3d657dc51ce400ed95a3015.png)
Die Lösungsmenge für diesen Fall ist somit
![\mathbb{L}_1 = \; ]2;\; 7[](../_images/math/d5dc7825b64efdcf522b4fcc81715de1afee2e1d.png) .
.Für
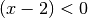 und
und 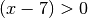 :
:![x - 2 < 0 \quad \text{ und } \quad x - 7 > 0 \\[4pt]
x < 2 \quad \text{ und } \quad x > 7 \\[4pt]](../_images/math/b82142ea15fc09c4464939e7285cf5d186ff9594.png)
Die Lösungsmenge für diesen Fall ist die leere Menge, also
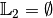 .
.
Die Gesamt-Lösungsmenge ist gleich der Vereinigungsmenge beider Fälle; es ist somit
![\mathbb{L} = \mathbb{L}_1 \cup \mathbb{L}_2 = \; ]2;\; 7[](../_images/math/783670593fc90f2abd33353366567b809accc3aa.png) .
.
Betragsungleichungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Betragsungleichungen.
Der Term
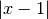 ist, sofern
ist, sofern 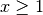 ist, identisch mit
ist, identisch mit
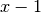 , andernfalls identisch mit
, andernfalls identisch mit 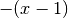 . Mit dieser
Fallunterscheidung ergibt sich:
. Mit dieser
Fallunterscheidung ergibt sich:Für
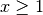 :
: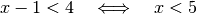
Die Lösungsmenge für diesen Fall ist somit
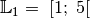 .
.Für
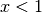 :
: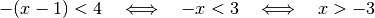
Die Lösungsmenge für diesen Fall ist somit
![\mathbb{L}_2 = \; ]\!-3;\; 1[](../_images/math/6c10601dc3e087754f4bb3ed738ad29020ed0b93.png) .
.
Die Gesamt-Lösungsmenge ist gleich der Vereinigungsmenge beider Fälle; es ist somit
![\mathbb{L} = \mathbb{L}_1 \cup \mathbb{L}_2 = \; ]\!-3;\; 5[](../_images/math/36ebe20a5ec1f440cdfcfb4355849961181643f3.png) .
.
