Lineare Gleichungssysteme¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Lineare Gleichungssysteme.
Multipliziert man die zweite Gleichung
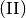 mit dem Faktor
mit dem Faktor
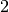 , so nehmen die Koeffizienten in der
, so nehmen die Koeffizienten in der  -Spalte die gleichen
Werte an:
-Spalte die gleichen
Werte an:![(\mathrm{I}): \quad 4 \cdot x_1 + 2 \cdot x_2 &= \;\,-6 \\
(\mathrm{II}): \quad 2 \cdot x_1 - 3 \cdot x_2 &= \;\,-7 \\[12pt]
\Rightarrow (\mathrm{I}): \quad 4 \cdot x_1 + 2 \cdot x_2 &= \;\,-6 \\
(2 \cdot \mathrm{II}): \quad 4 \cdot x_1 - 6 \cdot x_2 &= -14](../_images/math/b1b820d8e51d9e4e90c422cf5697f526c18d8e47.png)
Subtrahiert man nun beide Gleichungen voneinander, so bleibt die erste Zeile unverändert, während die zweite Zeile durch die Differenz aus der ersten und zweiten Gleichung ersetzt wird.
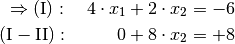
Die zweite Zeile stellt nun eine Gleichung mit nur einer Unbekannten dar; beim Auflösen dieser Gleichung erhält man das Ergebnis
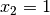 . Setzt
man diesen Wert für
. Setzt
man diesen Wert für 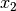 in die Gleichung
in die Gleichung 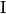 ein, so
erhält man für die andere Unbekannte:
ein, so
erhält man für die andere Unbekannte: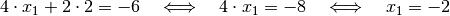
Das Gleichungssystem hat somit die Lösung
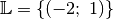 .
.
Bezeichnet man die Anzahl an Sätzen, die der erste Spieler gewonnen hat, mit
 und entsprechend die Anzahl der vom anderen Spieler gewonnenen
Sätze mit
und entsprechend die Anzahl der vom anderen Spieler gewonnenen
Sätze mit 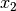 , so entspricht das Rätsel folgendem linearen
Gleichungssystem:
, so entspricht das Rätsel folgendem linearen
Gleichungssystem: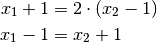
Dieses Gleichungssystem kann beispielsweise dadurch gelöst werden, indem man die zweite Gleichung nach
 auflöst; man erhält dadurch
auflöst; man erhält dadurch 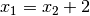 . Setzt man diesen Ausdruck für
. Setzt man diesen Ausdruck für 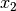 in die erste Gleichung
ein, so erhält man:
in die erste Gleichung
ein, so erhält man: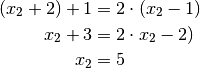
Der zweite Spieler hat somit insgesamt
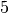 Sätze gewonnen, der erste
wegen der Beziehung
Sätze gewonnen, der erste
wegen der Beziehung 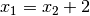 insgesamt
insgesamt 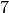 Sätze.
Sätze.
 Ein lineares Gleichungssystem mit drei Gleichungen und zwei
Unbekannten hat genau dann eine Lösung, wenn es bei Betrachtung von nur zwei
der drei Gleichungen eine Lösung hat und diese auch für die dritte Gleichung
gilt.
Ein lineares Gleichungssystem mit drei Gleichungen und zwei
Unbekannten hat genau dann eine Lösung, wenn es bei Betrachtung von nur zwei
der drei Gleichungen eine Lösung hat und diese auch für die dritte Gleichung
gilt.![(\mathrm{I}): \qquad \phantom{+}2 \cdot x_1 + 8 \cdot x_2 &= \phantom{+2}4 \\[4pt]
(\mathrm{II}): \qquad -5 \cdot x_1 + 4 \cdot x_2 &= \phantom{+}20 \\[4pt]
(\mathrm{III}): \qquad \phantom{+}7 \cdot x_1 + 4 \cdot x_2 &= -16](../_images/math/f83bd2a8d76291fc0a461f0343e4b242c39580fb.png)
Es genügt also, zunächst beispielsweise folgendes Gleichungsystem zu betrachten:
![(\mathrm{I}): \qquad \phantom{+}2 \cdot x_1 + 8 \cdot x_2 &= \phantom{2}4 {\color{white}...}\\[4pt]
(\mathrm{II}): \qquad -5 \cdot x_1 + 4 \cdot x_2 &= 20](../_images/math/9031f90c9f0570e3c622b591a49e514d7e6f2073.png)
Multipliziert man die zweite Gleichung mit dem Faktor
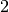 , so kann man
diese von der ersten Gleichung subtrahieren, um das Gleichungssystem auf eine
Gleichung mit nur noch einer Unbekannten zu reduzieren:
, so kann man
diese von der ersten Gleichung subtrahieren, um das Gleichungssystem auf eine
Gleichung mit nur noch einer Unbekannten zu reduzieren:![(\mathrm{I}): \qquad \phantom{+1}2 \cdot x_1 + 8 \cdot x_2 &= \phantom{2}4 {\color{white}\qquad \quad ...}\\[4pt]
(2 \cdot \mathrm{II}): \qquad -10 \cdot x_1 + 8 \cdot x_2 &= 40 \\[12pt]
(\mathrm{I} - 2 \cdot \mathrm{II}): \qquad \;\phantom{+}12 \cdot x_1 \phantom{+8 \cdot x_2} &= -36](../_images/math/4a658f3444c8dd3d1071e566547633cf2e768cee.png)
Diese Gleichung liefert
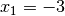 als Ergebnis. Setzt man diesen Wert für
als Ergebnis. Setzt man diesen Wert für
 in die erste Gleichung ein, so erhält man für
in die erste Gleichung ein, so erhält man für 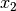 :
: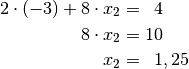
Nun ist zu prüfen, ob auch die dritte Gleichung durch die Variablen-Werte
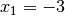 und
und 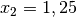 erfüllt wird:
erfüllt wird:![\phantom{+}7 \cdot (-3 ) + 4 \cdot (1,25) &= -16\\[4pt]
-21 + 5 &= -16 \quad \checkmark](../_images/math/cd599ed4ddca902dd531ac21a02707d63407c003.png)
Die gefundene Lösung erfüllt auch die dritte Gleichung. Das Gleichungssystem hat somit eine eindeutige Lösung, und zwar
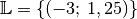 .
.
 Wiederum betrachtet man zunächst nur zwei der drei
Gleichungen. Multipliziert man beispielsweise die dritte Gleichung mit
Wiederum betrachtet man zunächst nur zwei der drei
Gleichungen. Multipliziert man beispielsweise die dritte Gleichung mit
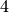 und addiert sie zur zweiten, so erhält man eine neue Gleichung, die
nur die Variable
und addiert sie zur zweiten, so erhält man eine neue Gleichung, die
nur die Variable  als Unbekannte hat:
als Unbekannte hat:![(\mathrm{II}): \quad \phantom{+}5 \cdot x_1 - 4 \cdot x_2 &= \;\,-2 \\[4pt]
(\mathrm{4 \cdot III}): \quad -8 \cdot x_1 + 4 \cdot x_2 &= -16\\[20pt]
(\mathrm{II} + 4 \cdot \mathrm{III}): \quad -3 \cdot x_1 \phantom{+ 4 \cdot x_2} &= -18](../_images/math/3c52fee765d87bc9255631ec55b4c2ba5b64b05a.png)
Aus dieser Gleichung folgt
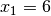 . Setzt man diesen Wert für
. Setzt man diesen Wert für
 in Gleichung
in Gleichung 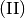 ein, so erhält man für
ein, so erhält man für
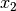 :
: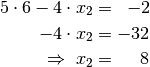
Nun ist zu prüfen, ob auch Gleichung
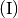 durch die
Variablen-Werte
durch die
Variablen-Werte 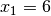 und
und 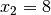 erfüllt wird:
erfüllt wird: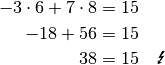
Die gefundene Lösung erfüllt zwar die zweite und dritte, nicht jedoch die erste Gleichung. Das Gleichungssytem ist somit nicht lösbar, die Lösungsmenge ist also die leer:
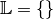 .
.
Bei einem Gleichungssystem mit drei Unbekannten und nur zwei Gleichungen stellt die dritte Variable einen frei wählbaren Parameter dar; das Gleichungssystem kann folglich nur in Abhängigkeit dieser Variablen gelöst werden.
Im konkreten Fall soll das Gleichungssystem in Abhängigkeit von der Variablen
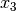 gelöst werden. Hierzu sortiert man diese als erstes auf die rechte
Seite des Gleichungssystems (so, als ob es sich dabei um einen gewöhnlichen
Zahlenwert handeln würde). Man erhält:
gelöst werden. Hierzu sortiert man diese als erstes auf die rechte
Seite des Gleichungssystems (so, als ob es sich dabei um einen gewöhnlichen
Zahlenwert handeln würde). Man erhält:![(\mathrm{I}): \quad \phantom{+}1 \cdot x_1 + 2 \cdot x_2 &= -6 -2 \cdot x_3 \\[4pt]
(\mathrm{II}): \quad -1 \cdot x_1 + 2 \cdot x_2 &= \phantom{-}4 +1 \cdot x_3](../_images/math/b2b35b718ed6749db50e3d1ffa571389692081ec.png)
Dieses Gleichungssystem kann man beispielsweise lösen, indem man die zweite Gleichung von der ersten subtrahiert. Man erhält dann als Gleichung für
 :
:![(\mathrm{I - II}): \quad \phantom{+}2 \cdot x_1 \phantom{+ 0 \cdot x_2 } &= -10 - 3 \cdot x_3 \\[4pt]
\Rightarrow \qquad \phantom{2 \cdot }x_1 \phantom{+ 0 \cdot x_2 } &= -\phantom{1}5 - 1,5 \cdot x_3](../_images/math/4c54257e6dcd2553a5eb9ec00fd1c4931978bead.png)
Somit ist
 in Abhängigkeit von
in Abhängigkeit von 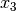 bestimmt. Setzt man
diesen Ausdruck für
bestimmt. Setzt man
diesen Ausdruck für  in die zweite Gleichung ein, so erhält man für
in die zweite Gleichung ein, so erhält man für
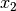 :
:![-1 \cdot (-5 - 1,5 \cdot x_3) + 2 \cdot x_2 & = \phantom{-}4 + 1 \cdot x_3 \\[4pt]
+5 + 1,5 \cdot x_3 + 2 \cdot x_2 & = \phantom{-}4 + 1 \cdot x_3 \\[4pt]
2 \cdot x_2 & = -1 - 0,5 \cdot x_3 \\[4pt]
x_2 & = -0,5 - 0,25 \cdot x_3](../_images/math/f78f4239124b1579f85cb7103e394e32d3b008df.png)
Die Lösungsmenge des Gleichungssystems in Abhängigkeit von
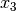 lautet
somit
lautet
somit 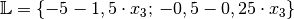 .
.
