Lineare Gleichungssysteme¶
Oftmals werden bei mathematischen Aufgaben nicht einzelne Gleichungen, sondern vielmehr Kombinationen von mehreren Gleichungen mit mehreren Unbekannten betrachtet. Damit ein solches Gleichungssystem eindeutig gelöst werden kann, müssen (mindestens) ebenso viele Gleichungen vorliegen wie Unbekannte vorhanden sind.
Sind die einzelnen Gleichungen eines Gleichungssystems linear, treten die
Variablen 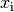 also nur erster Potenz auf, so spricht man von
einem linearen Gleichungssystem.
also nur erster Potenz auf, so spricht man von
einem linearen Gleichungssystem.
Im einfachsten Fall besteht ein lineares Gleichungssystem aus zwei Gleichungen
mit zwei Unbekannten. Bezeichnet man diese Variablen mit  und
und
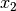 , so kann man das Gleichungssystem allgemein in folgender
Form darstellen:
, so kann man das Gleichungssystem allgemein in folgender
Form darstellen:
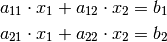
Die so genannten Koeffizienten 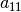 bis
bis
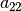 sind reelle Zahlen. Die erste Ziffer ihrer Indizes gibt
jeweils die Zeilennummer, die zweite Ziffer die Spaltennummer an.
sind reelle Zahlen. Die erste Ziffer ihrer Indizes gibt
jeweils die Zeilennummer, die zweite Ziffer die Spaltennummer an. 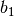 und
und 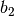 sind ebenfalls (reelle) Konstanten. Lösungen des
Gleichungssystems sind alle Zahlenpaare
sind ebenfalls (reelle) Konstanten. Lösungen des
Gleichungssystems sind alle Zahlenpaare 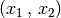 , die
sowohl die erste als auch die zweite Gleichung erfüllen.
, die
sowohl die erste als auch die zweite Gleichung erfüllen.
Eine einzelne Gleichung mit zwei voneinander unabhängigen Variablen lässt sich niemals eindeutig lösen. Die Werte der einen Variablen lassen sich lediglich in Abhängigkeit von der anderen Variablen angeben, wobei im Allgemeinen unendlich viele Zahlenpaare als Lösungen existieren. Auf derartige (funktionale) Zusammenhänge wird im Rahmen der Analysis näher eingegangen.
Grundlegende Lösungsverfahren¶
Ein lineares Gleichungssystem der obigen Form lässt sich mit verschiedenen Methoden lösen, die sich hinsichtlich ihres Rechenaufwands erheblich voneinander unterscheiden. Um dies zu demonstrieren, werden die drei grundlegenden Verfahren im folgenden Abschnitt anhand des jeweils gleichen Beispiels vorgestellt. Dabei werden die Gleichungen zur besseren Übersichtlichkeit – wie allgemein üblich – mit römischen Ziffern durchnummeriert.
Einsetzungsverfahren:
Eine Gleichung kann nach einer Variablen, beispielsweise
, aufgelöst werden, und der sich ergebende Term an Stelle der entsprechenden Variablen in die andere Gleichung eingesetzt werden. Obwohl dies einfach klingt, bringt diese Methode den größten Rechenaufwand mit sich.
Beispiel:
Löst man beispielsweise die Gleichung
nach
auf, so folgt:
Setzt man den resultierenden Ausdruck für
in Gleichung
ein, so erhält man:
Setzt man das Ergebnis
in Gleichung
ein, so folgt schließlich:
Die Lösung des Gleichungssystems ist somit
.
Das Einsetzungsverfahren ist, wie man sich leicht vorstellen kann, für komplexere Gleichungssyteme nicht ohne erheblichen Rechenaufwand anwendbar.
Gleichsetzungsverfahren:
Löst man beide Gleichungen nach einer Variablen, beispielsweise
, auf, so können die jeweils resultierenden Terme gleichgesetzt werden. Man erhält somit eine einzelne lineare Gleichung mit nur einer Unbekannten.
Beispiel:
Setzt man die beiden Terme für
gleich, so ergibt sich folgende Gleichung, die gemäß der für lineare Gleichungen üblichen Methode nach
aufgelöst werden kann:
Setzt man das Ergebnis
wiederum in Gleichung
ein, so erhält man wie im ersten Beispiel
und damit als Lösung
.
Auch die Gleichsetzungsmethode ist offensichtlich mit einigem Rechenaufwand verbunden und wird daher in der Praxis nur in seltenen Fällen angewendet.
Das Additionsverfahren:
Werden zwei Gleichungen mit jeweils passenden Faktoren
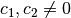 multipliziert, so kann erreicht werden, dass die Koeffizienten einer
Variablen, beispielsweise
multipliziert, so kann erreicht werden, dass die Koeffizienten einer
Variablen, beispielsweise  , einen betraglich gleichen Wert mit
unterschiedlichem Vorzeichen annehmen.
, einen betraglich gleichen Wert mit
unterschiedlichem Vorzeichen annehmen.Anschließend geht man von der Annahme aus, dass ein Zahlenpaar
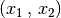 als Lösung des Gleichungssystems existiert. Dadurch kann
beispielsweise die erste Gleichung zur zweiten addiert werden, da (wenn
als Lösung des Gleichungssystems existiert. Dadurch kann
beispielsweise die erste Gleichung zur zweiten addiert werden, da (wenn
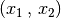 die Gleichung erfüllt) auf beiden Seiten das Gleiche
addiert wird.
die Gleichung erfüllt) auf beiden Seiten das Gleiche
addiert wird.Beispiel:
![\mathrm{(I)} : \qquad\qquad -\phantom{0}2 \cdot x_1 + \phantom{0}4 \cdot
x_2 &= -2 {\color{white} \;.}\\
\mathrm{(II)}: \qquad\qquad +\phantom{0}3 \cdot x_1 + \phantom{0}5 \cdot
x_2 &= +36 \\[12pt]](../_images/math/b5464616fc75ddbcce09bff2cd2497be84777dc0.png)
Wird die erste Gleichung mit
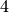 und die zweite Gleichung mit
und die zweite Gleichung mit 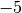 multipliziert, so nehmen die bei
multipliziert, so nehmen die bei  stehenden Koeffizienten
gleiche Werte mit unterschiedlichen Vorzeichen an.
stehenden Koeffizienten
gleiche Werte mit unterschiedlichen Vorzeichen an.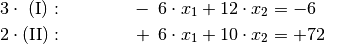
Unter der Annahme, dass ein Zahlenpaar
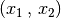 als Lösung
existiert, kann die erste Gleichung nun zur zweiten addiert werden. Hierbei
entfällt die Variable
als Lösung
existiert, kann die erste Gleichung nun zur zweiten addiert werden. Hierbei
entfällt die Variable  , und wieder ergibt sich eine einzige
Gleichung mit nur einer Unbekannten:
, und wieder ergibt sich eine einzige
Gleichung mit nur einer Unbekannten:
Setzt man das Ergebnis
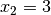 wiederum in Gleichung
wiederum in Gleichung
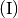 ein, so erhält man wie im ersten Beispiel
ein, so erhält man wie im ersten Beispiel 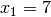 und damit als Lösung
und damit als Lösung 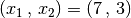 .
.Das Additionsverfahren ist im Allgemeinen mit dem geringsten Rechenaufwand verbunden und wird daher bevorzugt als grundlegende Lösungsmethode angewendet.
Die wesentliche Annahme des Additionsverfahrens, dass das Gleichungssystem eine eindeutige Lösung besitzt, trifft nicht für alle Gleichungsssysteme zu. Es kann dennoch auch dann angewendet werden, wobei im Allgemeinen die folgenden Fälle auftreten können
- Führt das Additionsverfahren auf eine Gleichung der Art
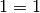 , so
entsprechen die beiden miteinander addierten Gleichungen einer einzigen
Gleichung und einem Vielfachen dieser Gleichung. Somit liegt letztlich eine
einzige Gleichung mit zwei Unbekannten vor, die im Allgemeinen nicht eindeutig
lösbar ist, sondern unendlich viele Zahlenpaare
, so
entsprechen die beiden miteinander addierten Gleichungen einer einzigen
Gleichung und einem Vielfachen dieser Gleichung. Somit liegt letztlich eine
einzige Gleichung mit zwei Unbekannten vor, die im Allgemeinen nicht eindeutig
lösbar ist, sondern unendlich viele Zahlenpaare 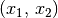 als
Lösung besitzt.
als
Lösung besitzt. - Führt das Additionsverfahren auf eine Gleichung der Art
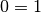 , also
einen Widerspruch, so existiert keine Lösung für das Gleichungssystem. (Dies
ist vergleichbar damit, dass es beispielsweise kein
, also
einen Widerspruch, so existiert keine Lösung für das Gleichungssystem. (Dies
ist vergleichbar damit, dass es beispielsweise kein  gibt, für das
zugleich
gibt, für das
zugleich 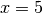 und
und 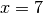 gilt.)
gilt.)
Das Additionsverfahren ist im Vergleich zum Einsetzungs- und Gleichsetzungsverfahren meist mit erheblich weniger Rechenaufwand verbunden; es stellt zugleich die Grundlage für den bei komplexeren Gleichungssystemen genutzten Gauss’schen Lösungsalgorithmus dar.
Der Gauss’sche Lösungsalgorithmus¶
Besteht ein Gleichungssystem aus mehr als zwei Gleichungen (mit mehr als zwei Unbekannten), so wird üblicherweise der nach Carl Friedrich Gauss benannte Algorithmus angewendet. Dieses Verfahren soll zunächst am Beispiel eines Gleichungssystems mit drei Gleichungen und drei Unbekannten demonstriert werden.
Ein Gleichungssystem mit drei Gleichungen und drei Unbekannten hat allgemein folgende Form:
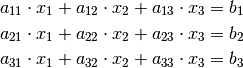
Um ein derartiges Gleichungssystem zu lösen, ist es hilfreich, dieses schrittweise in eine treppenartige Form zu bringen. Hierzu geht man nach folgendem Schema vor:
- Als erstes wird eine der Gleichungen ausgewählt („Ausgangsgleichung“).
- Mittels des Additionsverfahrens wird paarweise die Ausgangsgleichung und eine der beiden anderen Gleichungen mit passenden Faktoren multipliziert, um zu erreichen, dass die Koeffizienten der ersten Variablen jeweils betraglich gleiche Werte mit unterschiedlichen Vorzeichen annehmen.
- Die Ausgangsgleichung und je eine weitere Gleichung werden paarweise addiert, um ein Wegfallen der ersten Variablen zu erreichen.
- Das Gleichungssystem mit drei Gleichungen und drei Unbekannten ist so auf ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten reduziert worden.[1] Die obigen Verfahrensschritte können auf dieses erneut angewendet werden.
Der Gauss’sche Algorithmus führt somit Gleichungssysteme mit vielen Gleichungen beziehungsweise Unbekannten schrittweise auf Gleichungssysteme mit weniger Gleichungen und Unbekannten zurück, bis nur noch eine Gleichung mit einer Unbekannten übrig ist. Diese Gleichung kann einfach gelöst werden, und durch Einsetzen der Lösung in die Ausgangsgleichung(en) können wiederum schrittweise auch die Lösungen aller anderen Unbekannten mühelos berechnet werden.
Beispiel:
Wählt man in diesem Beispiel Gleichung
als Ausgangsgleichung und multipliziert sie mit drei, so kann man Gleichung
passenderweise mit Minus vier multiplizieren, um bei beiden Gleichungen identische Koeffizienten mit unterschiedlichem Vorzeichen für
zu erreichen. In gleicher Weise kann man Gleichung
unverändert lassen und Gleichung
mit zwei multiplizieren, um auch bei diesem Gleichungspaar identische Koeffizienten mit unterschiedlichem Vorzeichen für
zu erreichen:
Wird jeweils die Ausgangsgleichung zu den beiden anderen Gleichungen addiert, so erhält man ein neues Gleichungssystem mit zwei Gleichungen und zwei Unbekannten. Diese werden mit römischen Ziffern gemäß ihrer beiden ursprünglichen Gleichungen nummeriert und als Zeichen dafür, dass es sich um hergeleitete Gleichungen handelt, mit einem Hochkomma markiert:
Um das Additionsverfahren erneut anwenden zu können, müssen wiederum beide Gleichungen mit geeigneten Faktoren multipliziert werden, um betraglich gleiche Koeffizienten mit unterschiedlichen Vorzeichen für
zu erreichen. Dazu kann die neue Ausgangsgleichung
mit Minus sechs und die zweite Gleichung mit fünf multipliziert werden:
Eine Addition beider Gleichungen führt schließlich auf eine einzige Gleichung, die nur noch die Variable
beinhaltet.
Somit ist eine eindeutige Lösung für die Variable
gefunden. Um die Lösungen für die Variablen
und
zu berechnen, setzt man die gefundene Lösung zunächst in die vorherige Ausgangsgleichung
ein. Damit kann
einfach bestimmt werden:
Setzt man die Lösungen
und
schließlich in die erste Ausgangsgleichung
ein, so erhält man auch die Lösung für die letzte Variable
:
Damit sind alle Variablen bestimmt. Die Lösung des Gleichungssystems ist
.
Anmerkungen:
| [1] | Allgemein kann auf diese Weise ein Gleichungssystem mit  Gleichungen und
Gleichungen und  Unbekannten auf ein Gleichungssystem mit Unbekannten auf ein Gleichungssystem mit
 Gleichungen und Gleichungen und  Unbekannten reduziert werden. Unbekannten reduziert werden. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

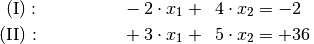
![{\color{white} \ldots \qquad }\mathrm{(I)}: \qquad\qquad \;\, \phantom{+ 004 \cdot x
_2}-2 \cdot x_1 &= -4 \cdot x_2 - 2 {\color{white}
0 } \\
\Rightarrow \qquad\qquad\qquad \phantom{+ 0004 \cdot x_2}
\phantom{1} x_1 &= +2 \cdot x_2 +1 \phantom{0} \\[10pt]](../_images/math/0120de3f773152545f00a0911fb137953f2e1b26.png)
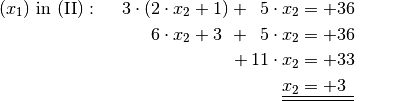
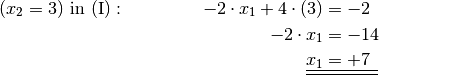
![{\color{white} \ldots \ldots\ldots}\mathrm{(I)} : \qquad\qquad
-\phantom{0}2 \cdot x_1 + \phantom{0}4 \cdot x_2 &= -2 {\color{white}
\;.}\\
\Rightarrow \qquad\qquad\qquad \phantom{+ 004 \cdot x_2} \phantom{1} x_1
&= +2 \cdot x_2 +1 \phantom{0} \\[12pt]
\mathrm{(II)}: \qquad\qquad +\phantom{0}3 \cdot x_1 + \phantom{0}5 \cdot
x_2 &= +36 \\
\Rightarrow \qquad\qquad\qquad \phantom{+ 004 \cdot x_2} \phantom{1} x_1
&= -\frac{5}{3} \cdot x_2 +12](../_images/math/5c277ebfaf83ad62add9252e2b95d87cce1b4b51.png)
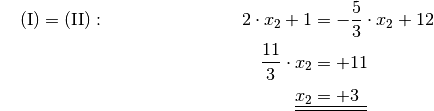
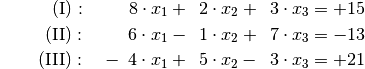
![3 \cdot \phantom{\mathrm{II}}\mathrm{(I)}: \quad \phantom{-}24 \cdot x_1 +
\phantom{0}6 \cdot x_2 + \phantom{0}9 \cdot x_3 &= + 45 \\
-4 \cdot \phantom{\mathrm{I}}\mathrm{(II)}: \quad -24 \cdot x_1
+\phantom{0}4 \cdot x_2 -28 \cdot x_3 &= +52 \\[12pt]
1 \cdot \phantom{\mathrm{II}}\mathrm{(I)}: \quad \phantom{-0}8 \cdot x_1 +
\phantom{0}2 \cdot x_2 + \phantom{0}3 \cdot x_3 &= + 15 \\
2 \cdot \mathrm{(III)}: \quad -\phantom{0}8 \cdot x_1 + 10 \cdot x_2 -
\phantom{0}6 \cdot x_3 &= +42 \\](../_images/math/c6578ec9e495e0ed8812fb8fbc14626e837a0dbc.png)
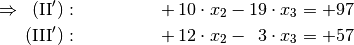
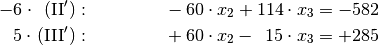

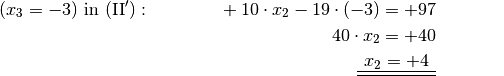
![\left.\begin{aligned}
(x_2 = +4) \\
(x_3 = -3)
\end{aligned}
\right\}
\text{ in } \mathrm{(I)}: \quad 8 \cdot x_1 +2 \cdot (+4)
+\phantom{0}3 \cdot (-3) = +15 {\color{white}\ldots \ldots
\ldots}\\[-10pt]
8 \cdot x_1 = +16 {\color{white}\ldots \ldots \ldots}\\
\underline{\underline{\phantom{_1}x_1 = +2 \phantom{_3}}}
{\color{white}\ldots \ldots \ldots}](../_images/math/e0a2ca12d434e57e4724ec97ac0b231cfc3c3d23.png)