Lineare Gleichungssysteme

Die folgenden Aufgaben beziehen sich auf den Abschnitt Lineare Gleichungssysteme.

  • Welche Lösung hat das folgende Gleichungssystem?

    (\mathrm{I}): \quad 4 \cdot x_1 + 2 \cdot x_2 &= -6 \\[4pt] (\mathrm{II}): \quad 2 \cdot x_1 - 3 \cdot x_2 &= -7

    Lösung

  • Am Ende eines Trainings prahlt ein Tennis-Spieler gegenüber dem anderen:
    „Hätte ich auch noch den letzten Satz gewonnen, so hätte ich insgesamt doppelt so viele Sätze gewonnen wie Du!“
    Daraufhin meint der andere:
    „Gib‘ doch nicht so an… hättest Du auch den vorletzten verloren, dann hätten wir jeweils gleich viele gewonnen!“
    Wie viele Sätze haben die beiden Spieler jeweils gewonnen?

    Lösung

  • Haben folgende Gleichungssysteme eine eindeutige Lösung? Wenn ja, wie lautet diese?

    \begin{array}{>{\arraybackslash$}p{1cm}<{$} >{\arraybackslash$}p{2.5cm}<{$} >{\arraybackslash$}p{1.5cm}<{$}} \text{a) } & \phantom{+}2 \cdot x_1 \, + \, 8 \cdot x_2 &= \phantom{+2}4 \\[4pt] & -5 \cdot x_1 \, + \, 4 \cdot x_2 &= \phantom{+}20 \\[4pt] & \phantom{+}7 \cdot x_1 \, + \, 4 \cdot x_2 &= -16\\[20pt] \text{b) } & \phantom{-}3 \cdot x_1 \, + \, 7 \cdot x_2 &= \phantom{+}15 \\[4pt] & \phantom{+}5 \cdot x_1 \, - \, 4 \cdot x_2 &= \;\;-2 \\[4pt] & -2 \cdot x_1 \, + \, 1 \cdot x_2 &= \;\;-4 \end{array}

    Lösung

  • Wie lautet die Lösungsmenge des folgenden Gleichungssystems in Abhängigkeit von x_3?

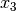    \phantom{+}1 \cdot x_1 + 2 \cdot x_2 + 2 \cdot x_3 &= -6 \\[4pt] - 1 \cdot x_1 + 2 \cdot x_2 - 1 \cdot x_3 &= \phantom{+}4

    Lösung