Bruch-, Produkt- und Wurzelgleichungen¶
Bruchgleichungen und Wurzelgleichungen stellen Gleichungstypen dar, die durch entsprechende Umformungen in eine algebraische Gleichung umgewandelt werden können.
Bruchgleichungen¶
Als Bruchgleichung wird eine Gleichung bezeichnet, in der die Variable  mindestens einmal im Nenner steht. Hierbei ist auf den Definitionsbereich der
Gleichung zu achten, da der Nenner eines Bruches niemals den Wert Null annehmen
darf („Definitionslücke“). Allgemein ist der Definitionsbereich einer
Bruchgleichung gleich den reellen Zahlen ohne die Lösungen der Gleichungen, die
sich ergeben, wenn man den im Nenner stehenden
mindestens einmal im Nenner steht. Hierbei ist auf den Definitionsbereich der
Gleichung zu achten, da der Nenner eines Bruches niemals den Wert Null annehmen
darf („Definitionslücke“). Allgemein ist der Definitionsbereich einer
Bruchgleichung gleich den reellen Zahlen ohne die Lösungen der Gleichungen, die
sich ergeben, wenn man den im Nenner stehenden  -Term bzw. die im Nenner
stehende
-Term bzw. die im Nenner
stehende  -Terme jeweils gleich Null setzt.
-Terme jeweils gleich Null setzt.
Um eine Bruchgleichung zu lösen, wendet man folgende Methode an:
- Zunächst werden die einzelnen Bruchterme durch passende Erweiterungen auf den Hauptnenner gebracht – wahlweise durch Multiplikation aller Nennerterme oder durch Bildung des kleinsten gemeinsamen Vielfachen der Nennerterme.[1]
- Multipliziert man dann die Gleichung mit dem Hauptnenner
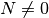 , so
entfallen alle Brüche (da der Hauptnenner in allen Bruchtermen gekürzt
werden kann beziehungsweise
, so
entfallen alle Brüche (da der Hauptnenner in allen Bruchtermen gekürzt
werden kann beziehungsweise  gilt).
gilt).
Die übrig bleibenden Terme stellen oftmals eine algebraische Gleichung dar, häufig ersten oder zweiten Grades, die mit Hilfe der in den vorherigen Abschnitten beschriebenen Verfahren gelöst werden kann.
Beispiel:
Die Lösungsmenge folgender Gleichung soll bestimmt werden:
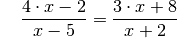
Damit keiner der beiden Nenner gleich Null ist, muss
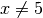 und
und
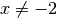 gelten.
Zur Lösung der Gleichung werden die Terme auf beiden Seiten mit dem
Hauptnenner
gelten.
Zur Lösung der Gleichung werden die Terme auf beiden Seiten mit dem
Hauptnenner 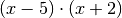 multipliziert. Beide Brüche können
anschließend gekürzt werden:
multipliziert. Beide Brüche können
anschließend gekürzt werden:![\frac{(4 \cdot x - 2\phantom{x}) \cdot (x-5) \cdot
(x+2)\phantom{.}}{\phantom{\ldots\,}(x-5)} &= \; \frac{(3 \cdot x + 8)
\cdot (x-5) \cdot (x+2)}{\phantom{xx}(x+2)} \\[8pt]
\Rightarrow \quad (4 \cdot x - 2) \cdot (x+2) \; &= \; (3 \cdot x + 8)
\cdot (x-5)](../../_images/math/003555cad8c99a3c01e15ba7b79023f0fd6b0311.png)
Die so gekürzte Gleichung entspricht einer algebraischen Gleichung zweiten Grades. Nach dem Ausmultiplizieren kann sie wie üblich umgeformt und gelöst werden:
![{\color{white}\ldots\;\;}4 \cdot x^2 + 8 \cdot x - 2 \cdot x -4 &= 3
\cdot x^2 - 15 \cdot x + 8 \cdot x - 40 \\[6pt]
\Rightarrow \quad 1 \cdot x^2 + 13 \cdot x + 36 &= 0](../../_images/math/0d5aa6542eeeefe0465c2f67cdc4413ea7b05405.png)
Nach der Mitternachtsformel gilt:
![{\color{white}\ldots\;\;\;}D = b^2 - 4 \cdot a \cdot c &= 13^2 - 4 \cdot
1 \cdot 36 = 25\\[8pt]
x_{\mathrm{1,2}} = \frac{-b \pm \sqrt{D}}{2 \cdot a} &= \frac{-13 \pm
5}{2} \\[6pt]
\Rightarrow \quad x_1 = -9 \quad &\text{und} \quad x_2 =
-4{\color{white}\;\; \ldots \quad \qquad}](../../_images/math/fd5f97ea47998c0b4a7ad297ad0e634fb1fe06d8.png)
Die Lösungsmenge der Bruchgleichung lautet somit
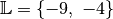 .
.
Verhältnisgleichungen¶
Ein (vergleichsweise) einfacher Sonderfall einer Bruchgleichung liegt vor, wenn
die Variable  nur ein einziges Mal auf einer Seite der Gleichung im
Nenner oder Zähler vorkommt, beispielsweise bei
nur ein einziges Mal auf einer Seite der Gleichung im
Nenner oder Zähler vorkommt, beispielsweise bei 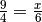 oder allgemein
oder allgemein 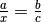 , wobei
, wobei 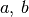 und
und  beliebige, aber bekannte Werte bezeichnen. Derartige
Gleichungen werden als Verhältnisgleichungen bezeichnet und können genutzt
werden, um eine unbekannte Größe zu berechnen, wenn drei andere Größen bekannt
sind und sich die Zahlenverhältnisse zwischen den Größen nicht ändern, die
Größen also zueinander „proportional“ sind.
beliebige, aber bekannte Werte bezeichnen. Derartige
Gleichungen werden als Verhältnisgleichungen bezeichnet und können genutzt
werden, um eine unbekannte Größe zu berechnen, wenn drei andere Größen bekannt
sind und sich die Zahlenverhältnisse zwischen den Größen nicht ändern, die
Größen also zueinander „proportional“ sind.
Steht die Variable  bei einer Verhältnisgleichung im Zähler eines
Terms, so genügt es, beide Seiten der Gleichung mit dem entsprechenden Nenner zu
multiplizieren, um den gesuchten Wert zu erhalten.
bei einer Verhältnisgleichung im Zähler eines
Terms, so genügt es, beide Seiten der Gleichung mit dem entsprechenden Nenner zu
multiplizieren, um den gesuchten Wert zu erhalten.
Beispiel:
Für ein Brotrezept werden
![\unit[500]{g}](../../_images/math/c9d6ca5148bb1ffc8b6d99f0ec65bccc3a16ada3.png) Mehl für
Mehl für ![\unit[800]{g}](../../_images/math/2fdf8027bf40d9d099693b680fd756258d3b50f3.png) Brot benötigt. Wieviel Gramm Mehl würde man (theoretisch) benötigen, um
Brot benötigt. Wieviel Gramm Mehl würde man (theoretisch) benötigen, um
![\unit[3000]{g}](../../_images/math/de4af46918746a8f297c94032130af7de105b57f.png) Brot zu backen?
Brot zu backen?Die gesuchte Mengenangabe
 steht hierbei im gleichen Verhältnis zur
Zahl
steht hierbei im gleichen Verhältnis zur
Zahl 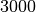 wie
wie  zu
zu 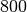 , also:
, also: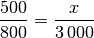
Multipliziert man beide Seiten der Gleichung mit
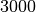 , so lässt sich
der gesuchte Wert (nach dem Kürzen des Bruchs) unmittelbar ablesen:
, so lässt sich
der gesuchte Wert (nach dem Kürzen des Bruchs) unmittelbar ablesen:
Für
![\unit[3000]{g}](../../_images/math/de4af46918746a8f297c94032130af7de105b57f.png) Brot wären somit
Brot wären somit ![\unit[1\,875]{g}](../../_images/math/29e977e9d48fa99befbdb2025d86a5f62efba898.png) Mehl
nötig.
Mehl
nötig.
Tipp: Steht die Variable  bei einer Verhältnisgleichung im Nenner,
so empfiehlt es sich, die Brüche auf beiden Seiten der Gleichung durch ihre
Kehrbrüche zu ersetzen; dadurch hat man die Aufgabe auf die obige Form
zurückgeführt. Es genügt dann wiederum, den Zahlenterm mit dem zur Variablen
gehörenden Nenner zu multiplizieren.
bei einer Verhältnisgleichung im Nenner,
so empfiehlt es sich, die Brüche auf beiden Seiten der Gleichung durch ihre
Kehrbrüche zu ersetzen; dadurch hat man die Aufgabe auf die obige Form
zurückgeführt. Es genügt dann wiederum, den Zahlenterm mit dem zur Variablen
gehörenden Nenner zu multiplizieren.
Produktgleichungen¶
Neben der obigen Form der (direkten) Proportionalität kann es auch vorkommen,
dass eine Größe immer kleiner wird, wenn eine andere Größe zunimmt.
Beispielsweise nimmt die Zeit, die man für eine bestimmte Wegstrecke benötigt,
mit zunehmender Geschwindigkeit ab. Ein solcher Zusammenhang zwischen zwei
Größen 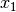 und
und 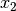 wird als indirekte Proportionalität
bezeichnet und kann formal als Produktgleichung geschrieben werden:
wird als indirekte Proportionalität
bezeichnet und kann formal als Produktgleichung geschrieben werden:
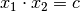
Hierbei ist  ein bekannter, konstanter Wert. Eine solche Gleichung kann
nur in zwei Fällen eindeutig gelöst werden:
ein bekannter, konstanter Wert. Eine solche Gleichung kann
nur in zwei Fällen eindeutig gelöst werden:
- wenn eine der beiden Größen
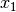 oder
oder 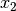 ein ebenfalls
bekannter Wert
ein ebenfalls
bekannter Wert  ist, die Gleichung also in der trivialen Form
ist, die Gleichung also in der trivialen Form
 mit der Lösung
mit der Lösung 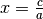 geschrieben
werden kann, oder
geschrieben
werden kann, oder - wenn eine zweite Gleichung für
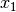 oder
oder 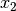 angegeben werden
kann. Bei indirekten Proportionalitäten handelt es bei dieser ebenfalls um
eine (triviale) Produktgleichung der Form
angegeben werden
kann. Bei indirekten Proportionalitäten handelt es bei dieser ebenfalls um
eine (triviale) Produktgleichung der Form 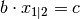 .
.
Bei vielen Aufgaben bleibt somit eine Gleichung mit nur einer Unbekannten, die allgemein folgende Form hat:
(1)¶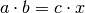
Zur besseren Lesbarkeit wurde hierbei der Index von  weggelassen, zumal
ohnehin nur eine Größe gesucht wird. Die Gleichung kann somit einfach gelöst
werden, indem durch den Faktor
weggelassen, zumal
ohnehin nur eine Größe gesucht wird. Die Gleichung kann somit einfach gelöst
werden, indem durch den Faktor  dividiert wird:
dividiert wird:

Die gesuchte Größe lässt sich also als Verhältnis der übrigen Größen beschreiben. Damit stimmen Produktgleichungen formal mit Verhältnisgleichungen überein, denn offensichtlich sind beide Gleichungsformen äquivalent:
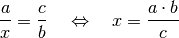
Es hängt von der Aufgabenstellung ab, ob eine Gleichung eher als Produkt- oder als Verhältnisgleichung angegeben wird; liegt zwischen zwei untersuchten Größen eine direkte Proportionalität vor, so wird der Zusammenhang meist als Verhältnisgleichung, bei indirekter Proportionalität als Produktgleichung angegeben.
Die Sonderform 
Eine Sonderform der Produktgleichung (1) liegt dann vor,
wenn die gesuchte Größe  der gegebenen Größe
der gegebenen Größe  entsprechen
soll, also die Lösung für eine Gleichung mit folgender Form gesucht wird:
entsprechen
soll, also die Lösung für eine Gleichung mit folgender Form gesucht wird:
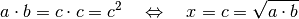
In diesem Fall wird 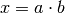 als mittlere Proportionale und
als mittlere Proportionale und
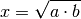 als geometrisches Mittel von
als geometrisches Mittel von  und
und
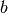 bezeichnet. Formal beschreibt
bezeichnet. Formal beschreibt  dabei das mittlere Folgenglied
einer geometrischen Folge, das zwischen
dabei das mittlere Folgenglied
einer geometrischen Folge, das zwischen  und
und 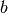 liegt; der konstante Faktor der Folge ist hierbei
liegt; der konstante Faktor der Folge ist hierbei 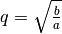 .
.
Dreisatz-Aufgaben¶
Wie die obigen Beispiele zeigen, lassen sich mit Verhältnis- und Produktgleichungen so genannte „Dreisatz-Aufgaben“ lösen. Diese heißen so, weil sie üblicherweise in drei Schritten gelöst werden:
Zunächst wird ein Bedingungssatz formuliert, der eine Aussage über das gegebene Größenverhältnis macht.
Beispiel: Ein Containerschiff benötigt für eine Strecke von
![s_1=\unit[800]{km}](../../_images/math/d3c096f91ff8e6cbce6b611d395114c023f49844.png) eine Zeit von
eine Zeit von ![t_1= \unit[16]{h}](../../_images/math/4654708e4794a5aa4ce002aa0d669cafd9c5a6e5.png) .
Der Bedingungssatz lautet also:
.
Der Bedingungssatz lautet also:![\unit[800]{km} \; \hat{=} \; \unit[16]{h}](../../_images/math/4e238ac46fefe247e98655f4e7715f6a12f799dd.png)
Über dem Ist-Gleich-Zeichen wird dabei häufig ein Dach-Symbol geschrieben, da die linke Seite der Gleichung mit der rechten Seite zwar in einem bestimmten Verhältnis seht, aber nicht mit dieser identisch ist.
Anschließend wird ein Fragesatz formuliert, der die gesuchte Größe
 beinhaltet. Der Fragesatz ergibt gemeinsam mit dem Bedingungssatz
ein System zweier Gleichungen, die aufgrund der festen Proportionalitäten als
eine Verhältnisgleichung geschrieben werden können.
beinhaltet. Der Fragesatz ergibt gemeinsam mit dem Bedingungssatz
ein System zweier Gleichungen, die aufgrund der festen Proportionalitäten als
eine Verhältnisgleichung geschrieben werden können.Beispiel: Wie lange braucht das obige Containerschiff für eine
![s_2 =
\unit[2500]{km}](../../_images/math/789fdd5f471c3851d2d540b0134bb6098a3dca78.png) lange Strecke? Der Fragesatz lautet in diesem Fall:
lange Strecke? Der Fragesatz lautet in diesem Fall:![\unit[2500]{km} \; \hat{=} \; ?](../../_images/math/a101c99b3cd0f187c7b504fce745695202a0c2bd.png)
Mit dem Schlußsatz wird die gesuchte Größe (
 oder
oder 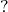 )
berechnet, indem jeweils das Verhältnis der linken und der rechten Seiten der
obigen Gleichungen gebildet wird. Vorzugsweise teilt man dabei die zweite
Gleichung durch die erste, so dass die gesuchte Größe im Zähler steht.
Es folgt für das obige Beispiel:
)
berechnet, indem jeweils das Verhältnis der linken und der rechten Seiten der
obigen Gleichungen gebildet wird. Vorzugsweise teilt man dabei die zweite
Gleichung durch die erste, so dass die gesuchte Größe im Zähler steht.
Es folgt für das obige Beispiel:![\frac{\unit[2500]{km}}{\unit[800]{km}} &= \frac{?}{\unit[16]{h}}](../../_images/math/a4539a438426675c1deb1cb60056a517417cc1cc.png)
Aus dem Schlusssatz kann die gesuchte Größe unmittelbar berechnet werden
![? &= \frac{25 \cdot \unit[16]{h}}{8} \\[4pt]
\Rightarrow \; ? &= \unit[50]{h}](../../_images/math/f89279c7bf8b062f51be8b7be93a923e61f772b1.png)
Bisweilen werden Dreisatz-Aufgaben auch gelöst, indem zunächst auf eine Einheit
der Grundgröße „herunter gerechnet“ wird; im obigen Beispiel könnte man
zunächst ausrechnen, wie lange das Schiff für eine Strecke von
![\unit[1]{km}](../../_images/math/dbbb21c49117e96b6d1e17caa7f69397f3e880c0.png) benötigt (Ergebnis:
benötigt (Ergebnis: ![\unit[0,02]{Stunden}](../../_images/math/85a06f4d72a37dbfe5adcb1fa889f7620e65513c.png) ).
Damit kann dann auf die gesuchte Zeit „hoch gerechnet“ werden, indem man die
Zeit je Kilometer mit der gegebenen Anzahl an Kilometern multipliziert. Im
Allgemeinen bedeutet dieses Lösungsverfahren gegenüber der oben genannten
Methode jedoch einen erhöhten Rechenaufwand.
).
Damit kann dann auf die gesuchte Zeit „hoch gerechnet“ werden, indem man die
Zeit je Kilometer mit der gegebenen Anzahl an Kilometern multipliziert. Im
Allgemeinen bedeutet dieses Lösungsverfahren gegenüber der oben genannten
Methode jedoch einen erhöhten Rechenaufwand.
Wurzelgleichungen¶
Als Wurzelgleichung wird eine Gleichung bezeichnet, in der die Variable
 mindestens einmal im Argument einer Wurzel steht. Hierbei muss
gegebenenfalls der Definitionsbereich der Variablen eingeschränkt werden, da im
Bereich der reellen Zahlen negative Wurzeln nicht definiert sind.[2]
mindestens einmal im Argument einer Wurzel steht. Hierbei muss
gegebenenfalls der Definitionsbereich der Variablen eingeschränkt werden, da im
Bereich der reellen Zahlen negative Wurzeln nicht definiert sind.[2]
Wurzelgleichungen lassen sich üblicherweise durch folgendes Verfahren lösen:
- Zunächst wird eine Wurzel durch geeignete Umformungen isoliert, also allein auf eine Seite der Gleichung gebracht.
- Anschließend werden beide Seiten der Gleichung mit dem Wurzelexponenten (bei einer Quadratwurzel mit zwei) potenziert. Falls bei der sich ergebenden noch immer Wurzeln auftreten, wiederholt man dieses Verfahren, bis alle Wurzeln eliminiert sind.
Die neue Gleichung entspricht oftmals einer algebraischen Gleichung, häufig ersten oder zweiten Grades, die mit Hilfe der in den vorherigen Abschnitten beschriebenen Verfahren gelöst werden kann.
Da das Potenzieren mit einem geradzahligen Exponenten keine Äquivalenzumformung darstellt, kann die umgeformte Gleichung (Schein-)Lösungen besitzen, die keine Lösungen der ursprünglichen Gleichung sind. Eine Probe durch Einsetzen der gefundenen Werte in die ursprüngliche Gleichung oder durch Vergleich der gefundenen Lösungen mit dem Definitionsbereich der Gleichung ist somit zwingend erforderlich.
Beispiel:
Die Lösungsmenge folgender Gleichung soll bestimmt werden:
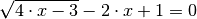
Damit unter der Wurzel kein negativer Wert steht, muss
 gelten, also
gelten, also  . Zur Lösung der Gleichung wird zunächst
die Wurzel isoliert, es werden also alle übrigen Terme auf die rechte Seite
der Gleichung gebracht:
. Zur Lösung der Gleichung wird zunächst
die Wurzel isoliert, es werden also alle übrigen Terme auf die rechte Seite
der Gleichung gebracht: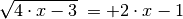
Nun kann die Gleichung quadriert werden. Es folgt:
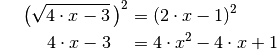
Die quadrierte Gleichung entspricht in diesem Fall einer algebraischen Gleichung zweiten Grades. Sie kann wie üblich umgeformt und gelöst werden:
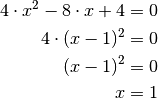
Der gefundene Wert
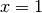 stellt auch, wie man durch Einsetzen leicht
überprüfen kann, eine Lösung der ursprünglichen Gleichung dar. Somit lautet
die Lösungsmenge der Wurzelgleichung
stellt auch, wie man durch Einsetzen leicht
überprüfen kann, eine Lösung der ursprünglichen Gleichung dar. Somit lautet
die Lösungsmenge der Wurzelgleichung  .
.
Anmerkungen:
| [1] | Das kleinste gemeinsame Vielfache (kgV) der Nennerterme lässt sich oftmals mit weniger Rechenaufwand berechnen, sofern diese in Form von (Linear-)Faktoren vorliegen. Das kgV ist in diesem Fall gleich dem Produkt der kleinsten Potenzen aller in den Nennern auftretenden Faktoren. Eine Zerlegung der Nennerterme in mehrere (Linear-)Faktoren ist genau dann
möglich, wenn bereits eine oder mehrere Definitionslücken
|
| [2] | Für jeden unter einer Wurzel stehenden Term 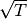 ist die
Ungleichung ist die
Ungleichung  zu lösen. Die
Definitionsmenge entspricht dann der Schnittmenge der Lösungsintervalle. zu lösen. Die
Definitionsmenge entspricht dann der Schnittmenge der Lösungsintervalle. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

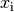 gefunden wurden. Mit Hilfe dieser Werte lassen sich
die Nennerterme jeweils als
gefunden wurden. Mit Hilfe dieser Werte lassen sich
die Nennerterme jeweils als  darstellen.
darstellen.