Exponential- und Logarithmusgleichungen

Exponentialgleichungen

Bei Exponentialgleichungen steht die Variable x im Exponenten mindestens eines Terms. Derartige Gleichungen sind im Allgemeinen nur näherungsweise unter Verwendung von Computerprogrammen lösbar.

In Spezialfällen sind Exponentialgleichungen allerdings auch bei Verwendung eines üblichen Taschenrechners lösbar, nämlich dann, wenn auf beiden Seiten ausschließlich konstante Terme oder Terme der Form 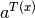a^{T(x)} stehen; 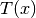T(x) soll dabei für einen beliebigen, von der Variablen x abhängigen Term stehen.

Wenn eine derartige Gleichung eine Lösung besitzt, also die linke Seite der Gleichung der rechten entspricht, dann muss ebenfalls der Logarithmus der linken und der rechten Seite gleich sein. Dieser Rechentrick ermöglicht die Verwendung der folgenden Identität:[1]

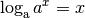
\log_{\mathrm{a}}{a^{x}} = x

Durch das „Logarithmieren“ einer Gleichung kann somit ein im Exponenten stehender, von der Variablen x abhängiger Term in einen gewöhnlichen Term umgewandelt werden. Dieser kann, je nach Art des Terms, weiter vereinfacht und ausgewertet werden.

Beispiele:

  • Die Lösung folgender Gleichung soll bestimmt werden:

    10^{2 \cdot x} = 50{\color{white}\qquad \qquad \quad \ldots}

    Das Logarithmieren beider Seiten führt auf folgende Gleichung:

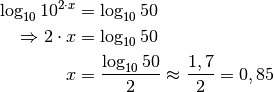
    \log_{10}{10^{2 \cdot x}} &= \log_{10}{50} \\ \Rightarrow 2 \cdot x &= \log_{10}{50} \\ x &= \frac{\log_{10}{50}}{2} \approx \frac{1,7}{2} = 0,85

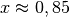    Somit hat die Gleichung die Lösung x \approx 0,85.

  • Die Lösung folgender Gleichung soll bestimmt werden:

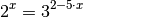
    2^{x} = 3^{2 - 5 \cdot x}{\color{white}\qquad \quad \ldots}

    Das Logarithmieren beider Seiten führt auf folgende Gleichung:

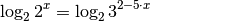
    \log_{2}{2^x} = \log_{2}{3^{2 - 5 \cdot x}}{\color{white}\qquad \quad \ldots}

    Hierbei können die Rechenregeln für Logarithmen genutzt werden. Da 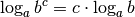\log_{a}{b^c} = c \cdot \log_{a}{b} gilt, kann die Gleichung weiter vereinfacht werden: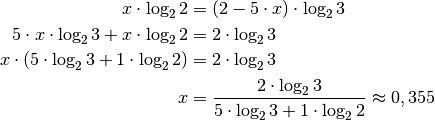

    x \cdot \log_{2}{2} &= (2 - 5 \cdot x) \cdot \log_{2}{3}{\color{white}\;\; \ldots}\\ 5 \cdot x \cdot \log_{2}{3} + x \cdot \log_{2}{2} &= 2 \cdot \log_{2}{3} \\ x \cdot (5 \cdot \log_{2}{3} + 1 \cdot \log_{2}{2} )&= 2 \cdot \log_{2}{3} \\ x &= \frac{2 \cdot \log_{2}{3}}{5 \cdot \log_{2}{3} + 1 \cdot \log_{2}{2}} \approx 0,355

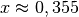    Somit hat die Gleichung die Lösung x \approx 0,355.

Tritt die Variable x sowohl im Exponenten eines Terms als auch als Basis eines anderen Terms auf, so ist die Gleichung nur näherungsweise mit Computerprogrammen lösbar. Besteht die Gleichung hingegen ausschließlich aus Termen mit gleicher Basis und der Variablen x im Exponenten, so heben sich die Exponentialterme durch das Logarithmieren gegenseitig auf, und es können ausschließlich die Exponenten verglichen werden.

Beispiel:

  • Die Lösungen folgender Gleichung soll bestimmt werden:

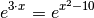
    e^{3 \cdot x} = e^{x^2-10}\\

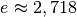    Hierbei bezeichnet e \approx 2,718 die Eulersche Zahl. Das Logarithmieren beider Seiten führt auf folgende Gleichung:

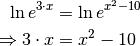
    \ln{e^{3 \cdot x}} &= \ln{e^{x^2 - 10}} \\ \Rightarrow 3 \cdot x &= x^2 - 10 \\

    Somit muss nur die sich ergebende quadratische Gleichung gelöst werden. Die Lösungen lassen sich in diesem Fall einfach mit dem Satz von Vieta bestimmen:

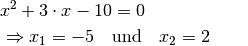
    x^2 + 3 \cdot x - 10 &= 0 \\ \Rightarrow x_1 = -5 \quad &\text{und} \quad x_2 = 2{\color{white} \quad \ldots}

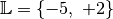    Die Lösungsmenge der Gleichung lautet somit \mathbb{L} = \{ -5,\; +2 \}.

Logarithmusgleichungen

Bei Logarithmusgleichungen tritt die Variable x mindestens einmal als Argument eines Logarithmus auf. Im Allgemeinen sind solche Gleichungen nur näherungsweise unter Verwendung von Computerprogrammen lösbar.

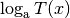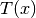Logarithmusgleichungen sind – ebenso wie Exponentialgleichungen – nur dann unter Verwendung eines üblichen Taschenrechners lösbar, wenn auf beiden Seiten ausschließlich konstante Terme oder Terme der Form \log_{\mathrm{a}}{T(x)} auftreten, wobei a die Basis des Logarithmus bezeichnet und T(x) für einen beliebigen, von der Variablen x abhängigen Term steht.

Wenn eine derartige Gleichung eine Lösung besitzt, also die linke Seite der Gleichung der rechten entspricht, dann muss die Gleichung ebenfalls gelten, wenn man eine der Basis a des Logarithmus entsprechende Zahl mit den Termen auf beiden Seiten potenziert. Dieser Rechentrick ermöglicht die Verwendung der folgenden Identität:[2]

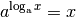
a^{\log_{\mathrm{a}}{x}} = x

Durch das „Exponenzieren“ einer Gleichung kann somit ein im Argument eines Logarithmus stehender, von der Variablen x abhängiger Term in einen gewöhnlichen Term umgewandelt werden. Dieser kann, je nach Art des Terms, weiter vereinfacht und ausgewertet werden.

Beispiel:

  • Die Lösung folgender Gleichung soll bestimmt werden:

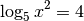
    \log_{5}{x^2} = 4

    Das Exponenzieren beider Seiten führt auf folgende Gleichung:

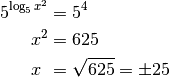
    5^{\log_{5}{x^2}} &= 5^4 \\ x^2 &= 625 \\ x\phantom{^3} &= \sqrt{625} = \pm 25

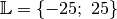    Somit hat die Gleichung die Lösungsmenge \mathbb{L} = \{ -25;\; 25 \}.

Anmerkungen:

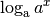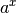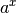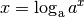[1]Der Logarithmus \log_{\mathrm{a}}{a^x} ist gleich derjenigen Zahl, mit der man a potenzieren muss, um a^x zu erhalten. Offensichtlich muss man a mit x potenzieren, um a^x zu erhalten. Somit ist x=\log_{\mathrm{a}}{a^x} für jede frei wählbare Basis a und beliebige Werte der Variablen x.
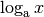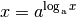[2]Der Logarithmus \log_{\mathrm{a}}{x} ist gleich derjenigen Zahl, mit der man a potenzieren muss, um x zu erhalten. Offensichtlich erhält man somit x, wenn man a mit dieser Zahl potenziert. Somit gilt x = a^{\log_{\mathrm{a}}{x}} für jede frei wählbare Basis a und beliebige Werte der Variablen x.

Hinweis

Zu diesem Abschnitt gibt es Übungsaufgaben.