Quadratische Gleichungen¶
Bei einer quadratischen Gleichung tritt die Variable  in der zweiten
Potenz
in der zweiten
Potenz 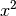 und gegebenenfalls zusätzlich in erster Potenz auf; sie darf
dabei nicht im Nenner stehen. Jede quadratische Gleichung kann durch äquivalente
Umformungen in die allgemeine Form gebracht werden:
und gegebenenfalls zusätzlich in erster Potenz auf; sie darf
dabei nicht im Nenner stehen. Jede quadratische Gleichung kann durch äquivalente
Umformungen in die allgemeine Form gebracht werden:
(1)¶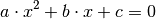
Hierbei sind 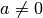 ,
,  und
und  beliebige Konstanten.
beliebige Konstanten.
Eine quadratische Gleichung hat höchstens zwei Lösungen. Wie viele und welche
Lösungen eine quadratische Gleichung im konkreten Fall hat, kann direkt bestimmt
werden, wenn die Gleichung in der allgemeinen Form vorliegt. Die Anzahl an
Lösungen ist durch den Wert ihrer so genannten „Diskriminante“  bestimmt, die anhand der allgemeinen Gleichungsform
(1) unmittelbar berechnet werden kann. Damit lassen
sich die folgenden drei Fälle unterscheiden:
bestimmt, die anhand der allgemeinen Gleichungsform
(1) unmittelbar berechnet werden kann. Damit lassen
sich die folgenden drei Fälle unterscheiden:
(2)¶![D > 0 \quad &\Leftrightarrow \quad \mathbb{L} = \Big \lbrace
\frac{-b - \sqrt{b^2 - 4 \cdot a \cdot c} }{2 \cdot a} ,\, \frac{-b +
\sqrt{b^2 - 4 \cdot a \cdot c} }{2 \cdot a} \Big \rbrace \\[4pt]
D = 0 \quad &\Leftrightarrow \quad \mathbb{L} =
\Big \lbrace \frac{-b}{2 \cdot a} \Big \rbrace \\[4pt]
D < 0 \quad &\Leftrightarrow \quad \mathbb{L} = \big \lbrace \big \rbrace](../../_images/math/4c6303b2871f9b587923e4b2039ded22b1fbae09.png)
Dieses Verfahren, anhand der Diskriminante 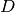 auf die Anzahl und die
Werte der Lösungen schließen zu können, wird umgangssprachlich auch als
„Mitternachtsformel“ bezeichnet.[1][2] Sie lässt sich auf jede quadratische
Gleichung anwenden, die in der allgemeinen Form (1)
vorliegt.
auf die Anzahl und die
Werte der Lösungen schließen zu können, wird umgangssprachlich auch als
„Mitternachtsformel“ bezeichnet.[1][2] Sie lässt sich auf jede quadratische
Gleichung anwenden, die in der allgemeinen Form (1)
vorliegt.
Sonderfälle quadratischer Gleichungen
Liegen Spezialfälle von quadratischen Gleichungen vor, so können auch andere, teilweise einfachere Lösungsverfahren genutzt werden:
Ist
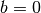 , so liegt eine quadratische Gleichung folgender Form
vor:
, so liegt eine quadratische Gleichung folgender Form
vor: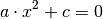
Diese Gleichung kann direkt nach
 aufgelöst werden:
aufgelöst werden: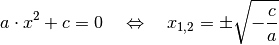
Die Gleichung hat nur dann die beiden obigen Lösungen, wenn
 und
und
 unterschiedliche Vorzeichen haben, andernfalls ist die Lösungsmenge
gleich
unterschiedliche Vorzeichen haben, andernfalls ist die Lösungsmenge
gleich 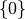 (falls
(falls 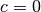 ist) oder gleich
der leeren Menge (falls
ist) oder gleich
der leeren Menge (falls 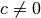 ist).
ist).Anschaulich ist die obige Gleichung daduch zu erklären, dass für das Quadrat jeder Zahl
 stets
stets 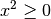 gilt. Wird nun eine Quadratzahl
mit einem positiven Faktor multipliziert, so kann man nicht eine weitere positive
Zahl hinzu addieren, um als Ergebnis den Wert Null zu erhalten.
gilt. Wird nun eine Quadratzahl
mit einem positiven Faktor multipliziert, so kann man nicht eine weitere positive
Zahl hinzu addieren, um als Ergebnis den Wert Null zu erhalten.Ist
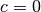 , fehlt also ein
, fehlt also ein  -freier Term, so liegt eine
quadratische Gleichung folgender Form vor:
-freier Term, so liegt eine
quadratische Gleichung folgender Form vor: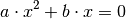
Die Mitternachtsformel liefert in diesem Fall die beiden Werte
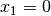 und
und 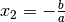 als Lösungen. Die gleichen Lösungen erhält
man, indem man auf der linken Seite der Gleichung
als Lösungen. Die gleichen Lösungen erhält
man, indem man auf der linken Seite der Gleichung  als gemeinsamen
Faktor ausklammert:
als gemeinsamen
Faktor ausklammert: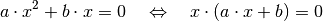
Da ein Produkt nur dann gleich Null ist, wenn (mindestens) einer der beiden Faktoren gleich Null ist, folgt aus der obigen Gleichungsform, dass entweder der
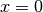 oder
oder 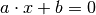 gelten muss. Aus dem ersten
Fall folgt
gelten muss. Aus dem ersten
Fall folgt 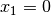 , aus dem zweiten Fall (einer linearen
Gleichung) folgt
, aus dem zweiten Fall (einer linearen
Gleichung) folgt 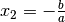 .
.
Ist
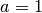 , so liegt eine „normierte“ quadratische Gleichung vor:
, so liegt eine „normierte“ quadratische Gleichung vor: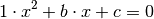
Jede allgemeine quadratische Gleichung mit
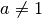 kann ebenfalls
mittels Division durch
kann ebenfalls
mittels Division durch  ebenfalls in eine normierte Form gebracht
werden. Setzt man
ebenfalls in eine normierte Form gebracht
werden. Setzt man 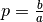 und
und 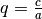 , so
lässt sich jede quadratische Gleichung in normierter Form darstellen:
, so
lässt sich jede quadratische Gleichung in normierter Form darstellen:(3)¶
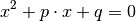
Sind
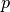 und
und 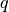 ganze Zahlen, so lassen sich die Lösungen der
Gleichung bisweilen auch schnell mit Hilfe des nach dem Mathematiker François
Viète benannten „Satz von Vieta“
bestimmen. Hierbei wird genutzt, dass zwischen den beiden möglichen Lösungen
ganze Zahlen, so lassen sich die Lösungen der
Gleichung bisweilen auch schnell mit Hilfe des nach dem Mathematiker François
Viète benannten „Satz von Vieta“
bestimmen. Hierbei wird genutzt, dass zwischen den beiden möglichen Lösungen
 und
und 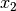 , für die auch
, für die auch 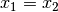 gelten kann,
folgender Zusammenhang besteht:[3]
gelten kann,
folgender Zusammenhang besteht:[3]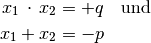
Kennt man die möglichen ganzzahligen Faktoren der Zahl
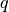 , so lässt
sich durch Kopfrechnen oftmals ein Zahlenpaar finden, das als Summe genau den
negativen Wert von
, so lässt
sich durch Kopfrechnen oftmals ein Zahlenpaar finden, das als Summe genau den
negativen Wert von 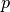 ergibt. Dieses Zahlenpaar stellt dann die
gesuchten Lösungen von Gleichung (3)
dar.[4]
ergibt. Dieses Zahlenpaar stellt dann die
gesuchten Lösungen von Gleichung (3)
dar.[4]
Produktform quadratischer Gleichungen
Sind  und
und 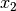 die Lösungen einer
quadratischen Gleichung, wobei auch
die Lösungen einer
quadratischen Gleichung, wobei auch 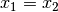 zulässig
ist, so kann diese allgemein auch in folgender Form dargestellt werden:
zulässig
ist, so kann diese allgemein auch in folgender Form dargestellt werden:
Eine solche Aufteilung einer Gleichung in mehrere lineare Faktoren wird als Linearfaktorzerlegung oder Produktform bezeichnet. Diese Darstellung spielt für quadratische Gleichungen nur eine untergeordnete Rolle, sie kann allerdings in nützlicher Weise auch bei Gleichungen höheren Grades angewendet werden.
Anmerkungen:
| [1] | Im ersten Fall
Im Fall |
| [2] | Die Gleichung (2) gilt,
sofern mit reellen Zahlen
Damit ergeben sich als Lösungen:
|
| [3] | Nach der „Mitternachtsformel“
(2) gilt mit
Ebenso gilt:
|
| [4] | Die „Mitternachtsformel“ (2) kann selbstverständlich ebenso zur Lösung von Gleichung (3) genutzt werden. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

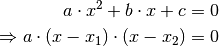
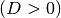 können die beiden Lösungen
können die beiden Lösungen 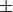 auch verkürzt in
folgender Form dargestellt werden:
auch verkürzt in
folgender Form dargestellt werden: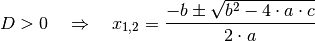
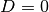 fallen die Lösungen
fallen die Lösungen 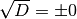 zusammen. Man spricht daher bisweilen auch von
einer „doppelten“ Lösung.
zusammen. Man spricht daher bisweilen auch von
einer „doppelten“ Lösung.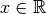 gerechnet wird. Rechnet
man mit
gerechnet wird. Rechnet
man mit 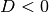 zwei Lösungen. In diesem Fall gilt:
zwei Lösungen. In diesem Fall gilt: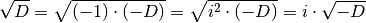
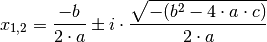
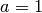 und
und
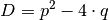 :
:![x_1 \cdot x_2 &= \frac{-p + \sqrt{D}}{2} \cdot \frac{-p -
\sqrt{D}}{2} \\[2pt]
&= \left(-\frac{p}{2} + \frac{\sqrt{D}}{2} \right) \cdot \left(- \frac{p}{2} -
\frac{\sqrt{D}}{2} \right) \\[2pt]
&= \Bigg( \!\! -\frac{p}{2} \; \Bigg)^2 - \left( \frac{\sqrt{D}}{2}\right)^2 \\
&= \;\; + \frac{p^2}{4} \quad \;\, - \quad \; \frac{D}{4} \\[2pt]
&= \;\; + \frac{p^2}{4} \quad \;\, - \left(\frac{p^2}{4} - q \right) \\[2pt] &= + q \qquad \checkmark](../../_images/math/56766fec9ef9964c324287912916f4645abef2d0.png)
![x_1 + x_2 &= \frac{-p + \sqrt{D}}{2} + \frac{-p -
\sqrt{D}}{2} \\[2pt]
&= \left(-\frac{p}{2} + \frac{\sqrt{D}}{2} \right) + \left(- \frac{p}{2} -
\frac{\sqrt{D}}{2} \right) \\[2pt]
&= -p \qquad \checkmark](../../_images/math/859fbf4fa6b7df7e9e3783124b9c88d0b3876935.png)