Die Einteilung der Zahlen¶
Natürliche Zahlen¶
Die Zahlen 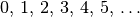 , die zum
Abzählen von Dingen verwendet werden, bezeichnet man als Menge der natürlichen
Zahlen
, die zum
Abzählen von Dingen verwendet werden, bezeichnet man als Menge der natürlichen
Zahlen 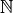 :
:
(1)¶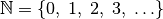
Die Menge der natürlichen Zahlen ohne die Zahl  wird mit dem Symbol
wird mit dem Symbol
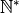 dargestellt.
dargestellt.
Ordnung der natürlichen Zahlen
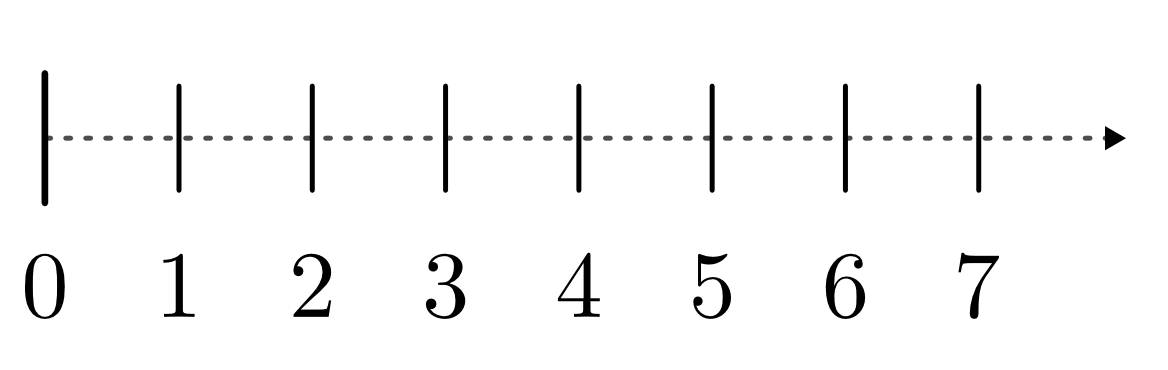
Mit Hilfe der natürlichen Zahlen kann man abzählen wie viele Elemente in einer Menge von Dingen enthalten sind, beispielsweise wie viele Äpfel sich in einer Kiste befinden.[1] Somit ist es auch möglich, die Anzahl an Elementen zweier verschiedener Mengen zu vergleichen, beispielsweise zu prüfen, ob sich in zwei Kisten jeweils gleich viele Äpfel befinden, oder in welcher Kiste mehr Äpfel enthalten sind.
Die Kisten können somit geordnet, also anhand der Anzahl der darin enthaltenen Äpfel sortiert werden. Als graphische Darstellungsform wird hierfür häufig ein „Zahlenstrahl“ gewählt, wobei die Zahlen ihrer Größe nach aufsteigend von links nach rechts angeordnet werden.
Rechnen mit natürlichen Zahlen
Jede Menge von Dingen lässt sich durch Hinzufügen weiterer Elemente vergrößern. Rechnerisch entspricht dies einer Addition zweier natürlicher Zahlen. Das Ergebnis einer Addition wird Summe genannt.
Ebenso kann eine Menge an Dingen durch Herausnehmen einzelner Elemente verkleinert werden, mit der Bedingung, dass nicht mehr Elemente aus der Menge herausgenommen werden können als in ihr enthalten sind. Rechnerisch entspricht dies einer Subtraktion zweier natürlicher Zahlen.[2] Das Ergebnis einer Subtraktion wird Differenz genannt.
Auch eine Multiplikation zweier natürlicher Zahlen ist stets möglich; sie entspricht rechnerisch einer mehrfachen Ausführung einer Addition. Das Ergebnis, Produkt genannt, ist erneut durch eine natürliche Zahl darstellbar, deren Größe dem jeweiligen Vielfachen der ursprünglichen Zahl entspricht.
Eine Division zweier natürlicher Zahlen, also ein Aufteilen einer Menge von Dingen nur auf mehrere Posten, ergibt ein ganzzahliges Ergebnis genau dann, wenn die Anzahl der Elemente in der Menge einem Vielfachen der Anzahl an Posten entspricht – ansonsten bleibt ein Rest übrig, der sich als Ganzes nicht weiter aufteilen lässt.
Ganze Zahlen¶
Um auch ein Fehlen an Dingen zahlenmäßig darzustellen, reichen die
natürlichen Zahlen nicht aus. Die Menge der natürlichen Zahlen
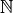 lässt sich jedoch zur Menge der ganzen Zahlen
lässt sich jedoch zur Menge der ganzen Zahlen
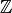 erweitern.
erweitern.
Die ganzen Zahlen als Obermenge der natürlichen Zahlen
Alle natürlichen Zahlen sind als Teilmenge in der Menge der ganzen Zahlen
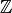 enthalten. Zusätzlich kommt für jede natürliche Zahl eine
entsprechende negative „Gegenzahl“ hinzu, die ein Fehlen des entsprechenden
Wertes ausdrückt. Zur Darstellung des Falles, dass kein Element vorhanden ist
(aber auch keines fehlt), wird die Zahl Null verwendet.
enthalten. Zusätzlich kommt für jede natürliche Zahl eine
entsprechende negative „Gegenzahl“ hinzu, die ein Fehlen des entsprechenden
Wertes ausdrückt. Zur Darstellung des Falles, dass kein Element vorhanden ist
(aber auch keines fehlt), wird die Zahl Null verwendet.
(2)¶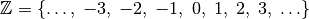
Die ganzen Zahlen lassen sich somit in gleicher Weise wie die natürlichen Zahlen als Zahlenstrahl darstellen. Dabei werden wiederum die einzelnen Zahlen ihrer Größe nach aufsteigend von links nach rechts geordnet.
Während bei negativen Zahlen das Minus-Zeichen stets dazu geschrieben werden muss, kann bei positiven Zahlen das Plus-Zeichen weggelassen werden.
Rechnen mit ganzen Zahlen
Durch die Erweiterung der natürlichen Zahlen um die negativen Zahlen kann mit Hilfe der ganzen Zahlen nicht nur jede Addition und Multiplikation, sondern auch jede Subtraktion uneingeschränkt ausgeführt werden.
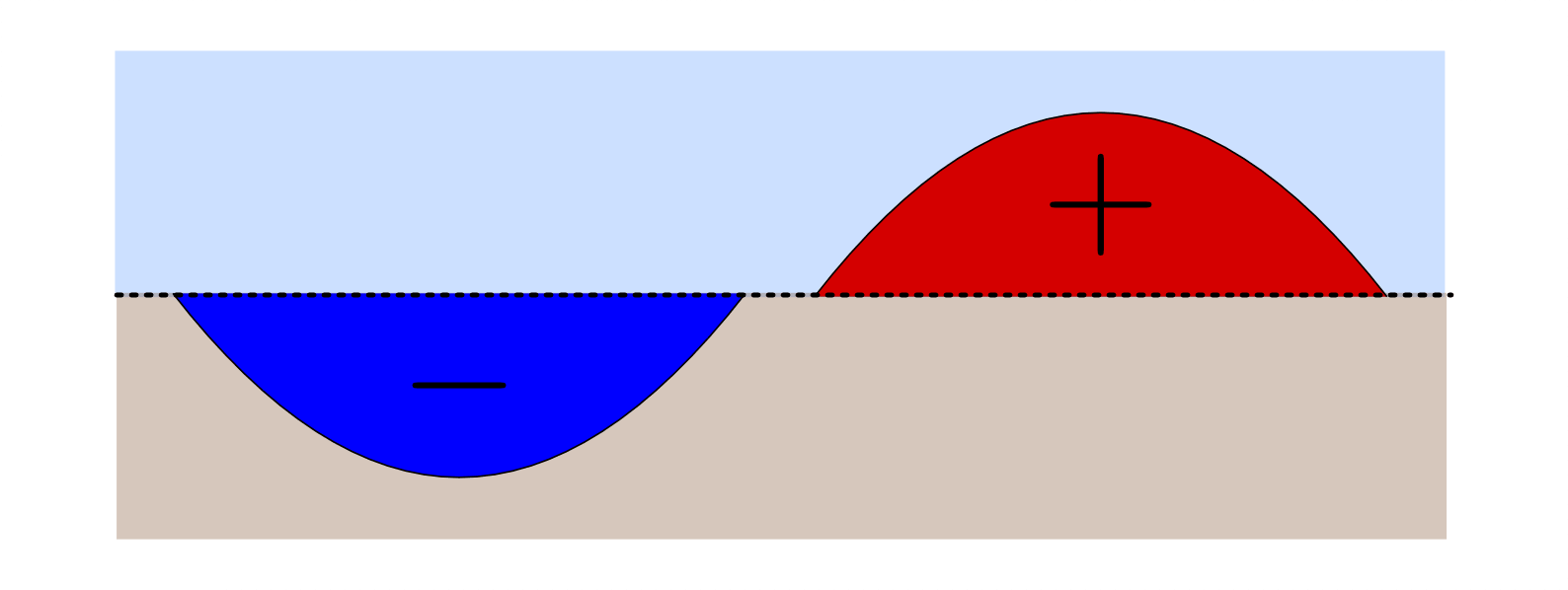
Eine veranschaulichende Darstellung von negativen Zahlen ist nicht unmittelbar möglich, da die Anzahl an Elementen einer Menge stets größer oder gleich Null ist – vielmehr lassen sich negative Zahlen als Mengenanzahlen auffassen, die entsprechend große positive Mengenanzahlen auszugleichen vermögen – so wie ein Haufen Erde ein entsprechend großes Erdloch ausfüllen kann.
Als Einschränkung bleibt jedoch auch im erweiterten System der ganzen Zahlen bestehen, dass eine Division zweier Zahlen nur dann möglich ist, wenn die erste Zahl (der Dividend) ein ganzzahliges Vielfaches der zweiten Zahl (des Divisors) ist – ansonsten bleibt bei der Division ein nicht weiter teilbarer Rest übrig.
Rationale Zahlen¶
Rationale Zahlen (manchmal auch „Bruchzahlen“ genannt) stellen eine Erweiterung des Zahlenbereichs der ganzen Zahlen dar, um auch eine allgemeine Division zweier (oder mehrerer) Zahlen zu ermöglichen.
Die rationalen Zahlen als Obermenge der ganzen Zahlen
Alle ganzen Zahlen sind als Teilmenge in der Menge der rationalen Zahlen
 enthalten. Zusätzlich kommen als weitere Elemente alle
Zahlen hinzu, die sich als Bruch zweier ganzer Zahlen
enthalten. Zusätzlich kommen als weitere Elemente alle
Zahlen hinzu, die sich als Bruch zweier ganzer Zahlen 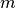 und
und
 darstellen lassen:
darstellen lassen:
(3)¶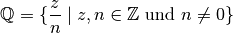
Die Zahl  oberhalb des Bruchstrichs wird Zähler genannt, die Zahl
oberhalb des Bruchstrichs wird Zähler genannt, die Zahl
 unterhalb des Bruchstrichs als Nenner des Bruchs bezeichnet. Die
einzige Bedingung liegt darin, dass nicht durch Null geteilt werden darf,
also
unterhalb des Bruchstrichs als Nenner des Bruchs bezeichnet. Die
einzige Bedingung liegt darin, dass nicht durch Null geteilt werden darf,
also 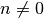 sein muss.[3]
sein muss.[3]
Auch die rationalen Zahlen lassen sich ihrer Größe nach als Zahlengerade anordnen; die ganzen Zahlen sind dabei als Teil der rationalen Zahlen an den entsprechenden Stellen eingebettet.[4]
Die rationalen Zahlen liegen „dicht“ beieinander, in den „Lücken“ zwischen je
zwei ganzen Zahlen treten also jeweils unendlich viele als rationale Zahlen
darstellbare Werte auf.
Anschaulich kann man sich dies dadurch erklären, dass beispielsweise jeder
natürlichen Zahl  ein Kehrwert
ein Kehrwert 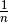 zugeordnet werden
kann, für den gilt:
zugeordnet werden
kann, für den gilt:
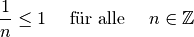
Betragsmäßig gilt das gleiche auch für Kehrwerte von negativen Zahlen; hierbei muss lediglich das Vorzeichen beachtet werden.[5]
Erweitern und Vereinfachen von Bruchzahlen
Eine Besonderheit rationaler Zahlen ist es, dass sich ein und die selbe Zahl
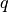 durch mehrere gleichwertige Brüche darstellen lässt. Es gilt:
durch mehrere gleichwertige Brüche darstellen lässt. Es gilt:

Allgemein kann jede Bruchzahl 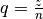 in eine andere, gleich
große Bruchzahl umgeformt werden, indem man sowohl den Zähler
in eine andere, gleich
große Bruchzahl umgeformt werden, indem man sowohl den Zähler  als
auch den Nenner
als
auch den Nenner  mit einer beliebigen ganzen Zahl multipliziert. Diese
in der Praxis häufig vorkommende Methode wird als „Erweitern“ einer Bruchzahl
beziehungsweise eines Bruches bezeichnet.
mit einer beliebigen ganzen Zahl multipliziert. Diese
in der Praxis häufig vorkommende Methode wird als „Erweitern“ einer Bruchzahl
beziehungsweise eines Bruches bezeichnet.
Beispiele:
- Anlässlich einer Feier möchte man Tortenstücke verteilen. Soll beispielsweise ein Gast ein Viertel einer Torte bekommen, so kann man dieses ebenso gut halbieren und somit zwei Achtel-Stücke servieren.
- Die wohl am häufigsten genutzte Umrechnung bezieht sich auf die Umrechnung einer Bruchzahl
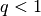 in eine wertgleiche Angabe mit dem Nenner
in eine wertgleiche Angabe mit dem Nenner
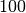 („Einhundertstel“ beziehungsweise „Prozent“ genannt).Ist z.B.
(„Einhundertstel“ beziehungsweise „Prozent“ genannt).Ist z.B.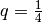 , so können Zähler und Nenner um den Faktor
, so können Zähler und Nenner um den Faktor
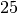 erweitert werden, und man erhält:
erweitert werden, und man erhält:
Somit entspricht der Bruch
 der Dezimalzahl
der Dezimalzahl 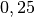 beziehungsweise der Prozentangabe
beziehungsweise der Prozentangabe 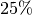 .
.
Im umgekehrten Fall kann eine Bruchzahl, deren Zähler und Nenner (mindestens) einen gemeinsamen Faktor besitzen, zu einer wertgleichen rationalen Zahl vereinfacht werden, indem der gemeinsame Faktor gekürzt wird (beziehungsweise die gemeinsamen Faktoren gekürzt werden).
Beispiel:
Bei der Bruchzahl
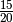 enthalten sowohl der Zähler als auch
der Nenner den gemeinsamen Faktor
enthalten sowohl der Zähler als auch
der Nenner den gemeinsamen Faktor 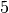 . Dieser kann „gekürzt“ werden:
. Dieser kann „gekürzt“ werden: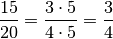
Bei der Bruchzahl
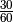 lässt sich der Zähler als Produkt der
Faktoren
lässt sich der Zähler als Produkt der
Faktoren 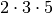 , der Nenner als
, der Nenner als  darstellen. Es können somit die Faktoren
darstellen. Es können somit die Faktoren 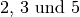 (beziehungsweise der Faktor
(beziehungsweise der Faktor 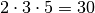 ) gekürzt werden:
) gekürzt werden: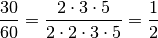
Derartige Umrechnungen werden beispielsweise bei Zeitangaben genutzt (eine „halbe“ Stunde usw).
Runden von Bruchzahlen
Jede rationale Zahl kann durch einen ganzzahligen Anteil und einen Restbruch dargestellt werden, dessen Wert kleiner als eins ist. Soll dieser Restbruch ebenfalls als Dezimalzahl angegeben werden, so können zwei unterschiedliche Fälle auftreten:
Manche Bruchzahlen lassen sich als Dezimalzahl mit endlich vielen Nachkomma-Stellen darstellen.
Beispiel:
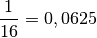
Manche Bruchzahlen entsprechen einer Dezimalzahl mit einer endlichen Periode. Bei derartigen Zahlen wiederholen sich ab einer bestimmten Stelle eine oder mehrere Nachkomma-Stellen unendlich oft.
Beispiele:
![\frac{1}{3} = 0,3\bar{3} = 0,3333 \ldots \\[8pt]](../_images/math/02b75d4a25f48947890012580f81779b0e4a87b6.png)
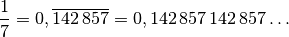
Bei der Rechnung mit Dezimalzahlen kann stets nur eine endliche Zahl an Nachkomma-Stellen berücksichtigt werden; rationale Zahlen werden daher entsprechend einer gewünschten Genauigkeit gerundet. Diese Genauigkeit wird durch die Angabe einer bestimmten Anzahl an „zählenden“ Ziffern, also Ziffern außer am Anfang oder am Ende stehenden Nullen, festgelegt.
Beispiele:
![\underbracket[0.5pt][5.pt]{78\,255\,300,00}_{10\text{ zählende Ziffern}}
\\[10pt]
0,000\,\!\!\!\!\!\!\!\!\underbracket[0.5pt][5.pt]{420\,800}_{6\text{
zählende Ziffern}}](../_images/math/1a14e8f020f0ff8cfa217e05059fae6a122d51d4.png)
Übermäßig viele zählende Ziffern täuschen bei Ergebnissen von Messungen oder
Schätzungen eine nicht gerechtfertigte Genauigkeit vor. Um dies zu vermeiden,
werden die jeweiligen Zahlen auf- beziehungsweise. abgerundet. Hierzu werden
zunächst die überflüssigen Ziffern durch Nullen ersetzt. Anschließend wird die
letzte nicht überflüssige Ziffer entweder um eins erhöht („Aufrunden“, falls die
erste überflüssige Ziffer 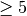 ist) oder unverändert gelassen
(„Abrunden“).
ist) oder unverändert gelassen
(„Abrunden“).
Bei physikalischen Größen wird anhand der Anzahl der zählenden Ziffern
implizit auch die Messgenauigkeit angegeben. Beispielsweise weist eine
Längenangabe von ![\unit[2,170]{m}](../_images/math/86d3cfa12c7b9bdd13ec70c1f6360b848375a5b8.png) auf eine Messgenauigkeit im
Millimeter-Bereich hin, während eine Angabe von
auf eine Messgenauigkeit im
Millimeter-Bereich hin, während eine Angabe von ![\unit[2,17]{m}](../_images/math/10ac55e78ff53dd8fe988863bff1ad60ef53947e.png) nur eine
Messgenauigkeit im Zentimeter-Bereich bedeutet.[6]
nur eine
Messgenauigkeit im Zentimeter-Bereich bedeutet.[6]
Um zu große Rundungsfehler zu vermeiden, sollte allerdings bei jeder Rechnung auf ein frühzeitiges Runden verzichtet und das Runden stattdessen erst am Ende (im Ergebnis) durchgeführt werden.
Rechnen mit rationalen Zahlen
Durch die Verwendung rationaler Zahlen lassen sich alle vier Grundrechen-Operationen – abgesehen von der Division durch Null – uneingeschränkt ausführen und beliebig miteinander kombinieren:
Die Addition zweier rationaler Zahlen
 und
und 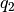 ist
definiert als:
ist
definiert als: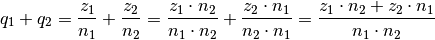
Um zwei rationale Zahlen
 und
und 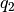 zu addieren, müssen sie
zunächst auf einen gemeinsamen Nenner
zu addieren, müssen sie
zunächst auf einen gemeinsamen Nenner  gebracht werden.
Beide Zahlen werden hierzu jeweils mit dem Nenner der anderen Zahl erweitert;
anschließend werden die (erweiterten) Zähler
gebracht werden.
Beide Zahlen werden hierzu jeweils mit dem Nenner der anderen Zahl erweitert;
anschließend werden die (erweiterten) Zähler  und
und
 miteinander addiert und auf den gemeinsamen Nenner
geschrieben.
miteinander addiert und auf den gemeinsamen Nenner
geschrieben.Die Subtraktion zweier rationaler Zahlen funktioniert nach dem gleichen Prinzip wie die Addition, es sind lediglich die Plus-Zeichen durch Minus-Zeichen zu ersetzen:
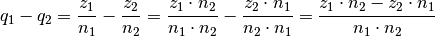
Die Multiplikation zweier rationaler Zahlen
 und
und 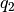 ist
definiert als:
ist
definiert als: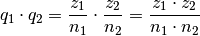
Um zwei rationale Zahlen
 und
und 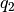 miteinander zu
multiplizieren, werden beide Zähler
miteinander zu
multiplizieren, werden beide Zähler 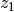 und
und 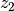 miteinander
multipliziert und das Ergebnis
miteinander
multipliziert und das Ergebnis  auf den gemeinsamen
Nenner
auf den gemeinsamen
Nenner  geschrieben.
geschrieben.Die Division zweier rationaler Zahlen
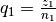 und
und
 entspricht einer Multiplikation der ersten Zahl
(des Dividenden) mit dem Kehrbruch der zweiten Zahl (des Divisors). Die
Division erfolgt somit nach dem gleichen Prinzip wie die Multiplikation, nur
müssen Zähler und Nenner der zweiten Zahl vertauscht werden:
entspricht einer Multiplikation der ersten Zahl
(des Dividenden) mit dem Kehrbruch der zweiten Zahl (des Divisors). Die
Division erfolgt somit nach dem gleichen Prinzip wie die Multiplikation, nur
müssen Zähler und Nenner der zweiten Zahl vertauscht werden:
Weitere Hinweise zum Rechnen mit rationalen Zahlen sind im Abschnitt Bruchrechnung beschrieben.
Reelle Zahlen¶
Eine Vielzahl an mathematischen Problemen kann nicht mit Hilfe der rationalen
Zahlen gelöst werden. Beispielsweise gibt es keine rationale Zahl  ,
welche die Gleichung
,
welche die Gleichung 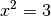 löst; ebenso gibt es keine rationale Zahl,
die das Verhältnis
löst; ebenso gibt es keine rationale Zahl,
die das Verhältnis 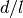 aus der Diagonale eines Quadrates und seiner
Seitenlänge beziehungsweise das Verhältnis
aus der Diagonale eines Quadrates und seiner
Seitenlänge beziehungsweise das Verhältnis 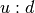 aus dem Umfang
aus dem Umfang  und dem Durchmesser
und dem Durchmesser  eines Kreises ausdrücken könnte. Um derartige
„Mängel“ zu beseitigen, lässt sich der Bereich der rationalen Zahlen zum Bereich
der reellen Zahlen erweitern.
eines Kreises ausdrücken könnte. Um derartige
„Mängel“ zu beseitigen, lässt sich der Bereich der rationalen Zahlen zum Bereich
der reellen Zahlen erweitern.
Die neu hinzukommenden Zahlen, beispielsweise 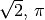 oder
oder
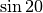 , werden dabei als „irrationale“ Zahlen bezeichnet. Sie lassen
sich zwar ihrem Wert nach in den Zahlenstrahl einordnen, lassen sich jedoch
durch keine rationale Zahl ausdrücken und besitzen in der Darstellung als
Dezimalzahl unendlich viele, nicht periodische Nachkommastellen.
, werden dabei als „irrationale“ Zahlen bezeichnet. Sie lassen
sich zwar ihrem Wert nach in den Zahlenstrahl einordnen, lassen sich jedoch
durch keine rationale Zahl ausdrücken und besitzen in der Darstellung als
Dezimalzahl unendlich viele, nicht periodische Nachkommastellen.
Für zwei besonders wichtige reelle Zahlen werden spezielle Symbole benutzt:
Die Zahl
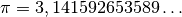 wird als „Kreiszahl“ bezeichnet. Sie
gibt den Zusammenhang zwischen dem Durchmesser
wird als „Kreiszahl“ bezeichnet. Sie
gibt den Zusammenhang zwischen dem Durchmesser  und dem Umfang
und dem Umfang
 eines Kreises an:
eines Kreises an:
- Die Zahl
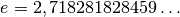 wird als „Eulersche Zahl“
bezeichnet. Sie ist in Verbindung mit Exponentialfunktionen und Logarithmen von
besonderer Bedeutung.
wird als „Eulersche Zahl“
bezeichnet. Sie ist in Verbindung mit Exponentialfunktionen und Logarithmen von
besonderer Bedeutung.
Rechnen mit reellen Zahlen
Mit Hilfe der reellen Zahlen lassen sich somit nicht nur alle vier Grundrechenarten – abgesehen von der Division durch Null – uneingeschränkt ausführen; auch das Potenzieren beliebiger und das Wurzelziehen nicht-negativer reeller Zahlen liefert stets eindeutige Ergebnisse.
Für die Potenz
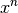 einer reellen Zahl
einer reellen Zahl  gilt mit
gilt mit 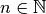 :
: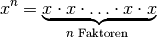
Eine Potenz
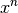 mit Exponent
mit Exponent  entspricht somit einer
entspricht somit einer
 -fachen Multiplikation der Grundzahl („Basis“)
-fachen Multiplikation der Grundzahl („Basis“)  mit sich
selbst. Das wohl bekannteste Beispiel hierfür sind die so genannten
„Zehner-Potenzen“
mit sich
selbst. Das wohl bekannteste Beispiel hierfür sind die so genannten
„Zehner-Potenzen“ 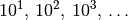 . Sie lassen sich
als Zehner-Stange, Hunderter-Quadrat und Tausender-Würfel darstellen.
. Sie lassen sich
als Zehner-Stange, Hunderter-Quadrat und Tausender-Würfel darstellen.
Das Wurzelziehen („Radizieren“) entspricht der Umkehrung des Potenzierens. Für eine beliebige reelle Zahl
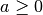 gelte folgende Gleichung:
gelte folgende Gleichung: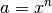 Dann ist mit gegebenem
Dann ist mit gegebenem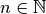 dem Wert nach genau eine
reelle Zahl
dem Wert nach genau eine
reelle Zahl  bestimmt, welche die Gleichung löst.Hierfür schreibt man:[7]
bestimmt, welche die Gleichung löst.Hierfür schreibt man:[7]![x = \sqrt[n]{a}](../_images/math/582a5207a8c03b200db4b0bb7e5fbc2eb61e5686.png)
Unter der
 -ten Wurzel aus einer nicht-negativen Zahl
-ten Wurzel aus einer nicht-negativen Zahl  versteht man somit diejenige Zahl
versteht man somit diejenige Zahl  , deren
, deren  -te Potenz gleich
-te Potenz gleich
 ist.
ist.Wohl am häufigsten treten die so genannten „Quadrat-Wurzeln“ einer Zahl
 auf. Hierbei wird diejenige Zahl
auf. Hierbei wird diejenige Zahl  gesucht, die, mit sich
selbst multipliziert, die Gleichung
gesucht, die, mit sich
selbst multipliziert, die Gleichung  löst. Beim Ergebnis
löst. Beim Ergebnis
![x = \sqrt[2]{a} = \sqrt{a}](../_images/math/3eb4ca96399fa31c6b4d66cbe797e7a8e37670c8.png) kann der „Wurzelexponent“
kann der „Wurzelexponent“  weggelassen werden.
weggelassen werden.
Berechnet man Quadrat-, Kubik- und allgemeinen Wurzeln mit Hilfe eines Taschenrechners oder Computers, so werden die häufig irrationalen Ergebnisse in gleicher Weise wie beim Runden von Bruchzahlen entsprechend der möglichen Anzeige-Genauigkeit gerundet.
Komplexe Zahlen¶
Komplexe Zahlen stellen eine Erweiterung des Zahlenbereichs der reellen Zahlen dar. Grundlegend hierfür waren Überlegungen von Gerolamo Cardano und Rafael Bombelli, auf welche Weise sich Wurzeln negativer Zahlen definieren ließen.
Der so geschaffene Zahlenbereich 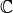 der komplexen Zahlen hat
sich für vielerlei Anwendungen in den Natur- und Ingenieurwissenschaften als
äußerst nützlich erwiesen. Eine komplexe Zahl lässt sich allerdings nicht mehr
durch eine einzelne Zahl darstellen, sondern bildet vielmehr ein geordnetes
Paar
der komplexen Zahlen hat
sich für vielerlei Anwendungen in den Natur- und Ingenieurwissenschaften als
äußerst nützlich erwiesen. Eine komplexe Zahl lässt sich allerdings nicht mehr
durch eine einzelne Zahl darstellen, sondern bildet vielmehr ein geordnetes
Paar 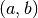 eines zweidimensionalen Vektorraums.
eines zweidimensionalen Vektorraums.
Da komplexe Zahlen in den derzeitigen Lehrplänen keine Beachtung finden, wird an dieser Stelle für interessierte Leser lediglich auf den Exkurs: Komplexe Zahlen verwiesen.
Anmerkungen:
| [1] | Eine Zahl, welche die Mächtigkeit einer endlichen Menge angibt, wird auch als Kardinalzahl bezeichnet. |
| [2] | Die Subtraktion stellt somit die „Umkehrung“ der Addition dar. |
| [3] | Eine Division durch
|
| [4] | Die ganzen Zahlen können als so genannte „Scheinbrüche“ aufgefasst
werden, d.h. Brüche, deren Nenner
Ein Scheinbruch liegt ebenfalls vor, wenn der Zähler
|
| [5] | Das Minus-Zeichen einer negativen rationalen Zahl wird für gewöhnlich vor den Bruchstrich geschrieben. Es ist allerdings genauso richtig, stattdessen entweder den Zähler oder den Nenner mit einem Minus-Zeichen zu versehen:
Tragen sowohl Zähler als auch Nenner ein Minus-Zeichen, so ist der Wert des Bruches positiv. |
| [6] | In der Physik richtet sich die Genauigkeitsangabe stets nach der ungenauesten Messung; die Anzahl an zählenden Ziffern des Ergebnisses ist also immer gleich der Anzahl der zählenden Ziffern der ungenauesten Messung beziehungsweise Maßangabe. |
| [7] | Genau genommen gilt dies nur, wenn  eine ungerade Zahl ist.
Für Wurzeln mit geradzahligen eine ungerade Zahl ist.
Für Wurzeln mit geradzahligen  erfüllt neben erfüllt neben ![x =
\sqrt[n]{a}](../_images/math/49ffb0ed7f98e79509e320c1109e257847ab349f.png) auch auch ![x = - \sqrt[n]{a}](../_images/math/4859a1de45aa932d8f9d1fda5b4965448ae7fbf4.png) die Bedingung die Bedingung  .
In diesem Fall heben sich beim Potenzieren, d.h. beim mehrfachen
Multiplizieren, die negativen Vorzeichen paarweise gegenseitig auf. (Siehe
auch Rechenregeln für Potenzen) .
In diesem Fall heben sich beim Potenzieren, d.h. beim mehrfachen
Multiplizieren, die negativen Vorzeichen paarweise gegenseitig auf. (Siehe
auch Rechenregeln für Potenzen) |

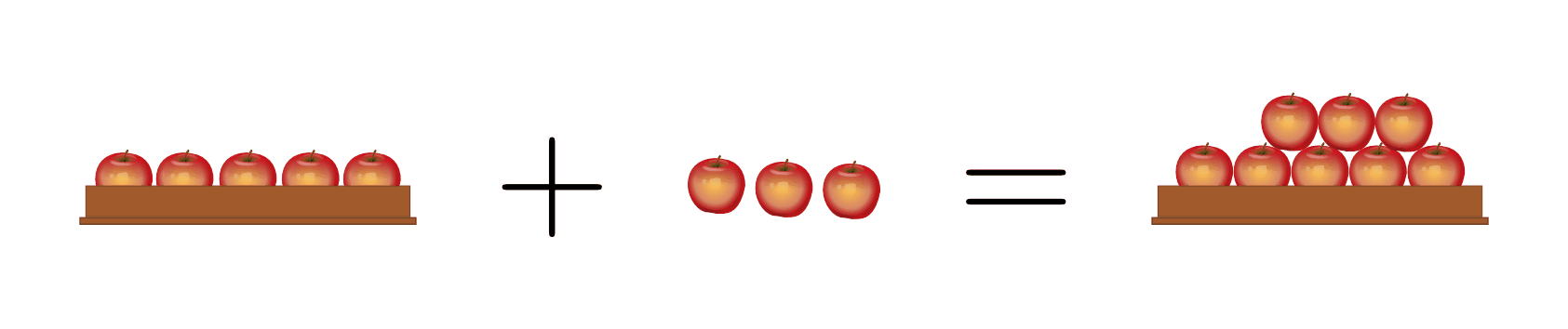

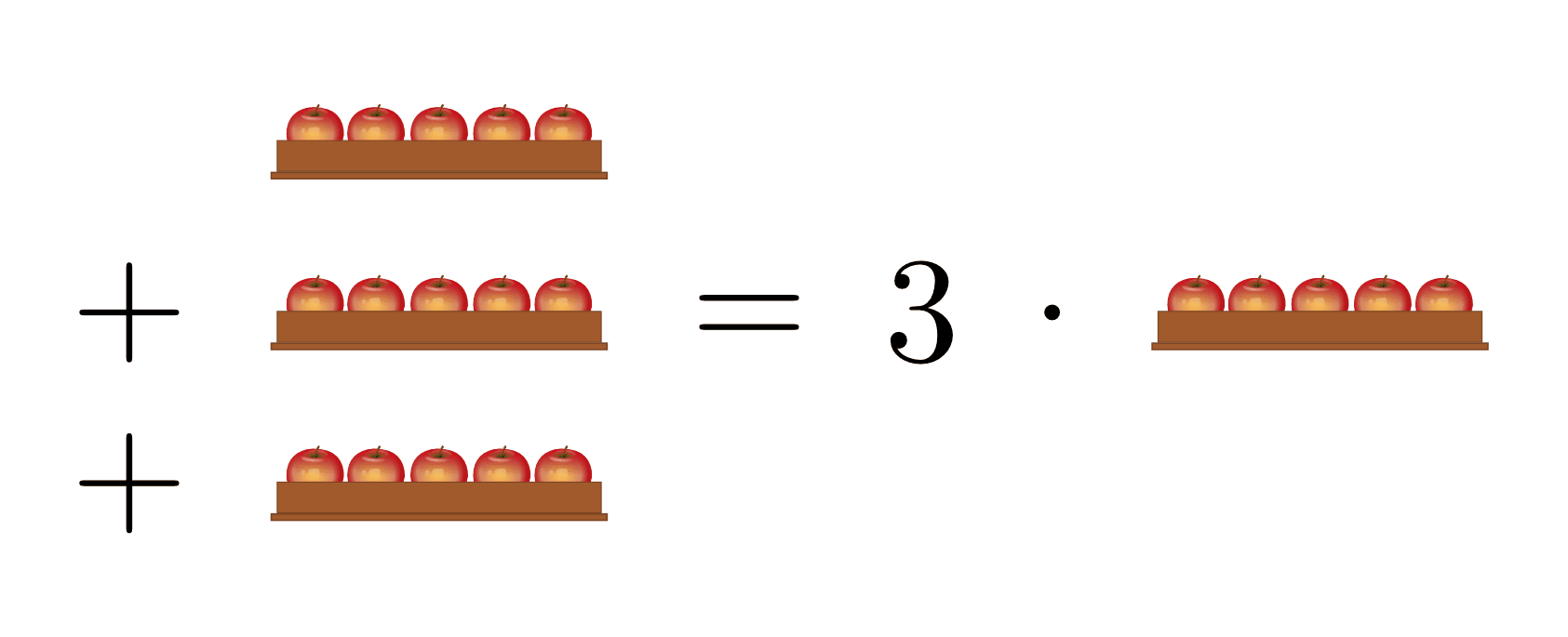
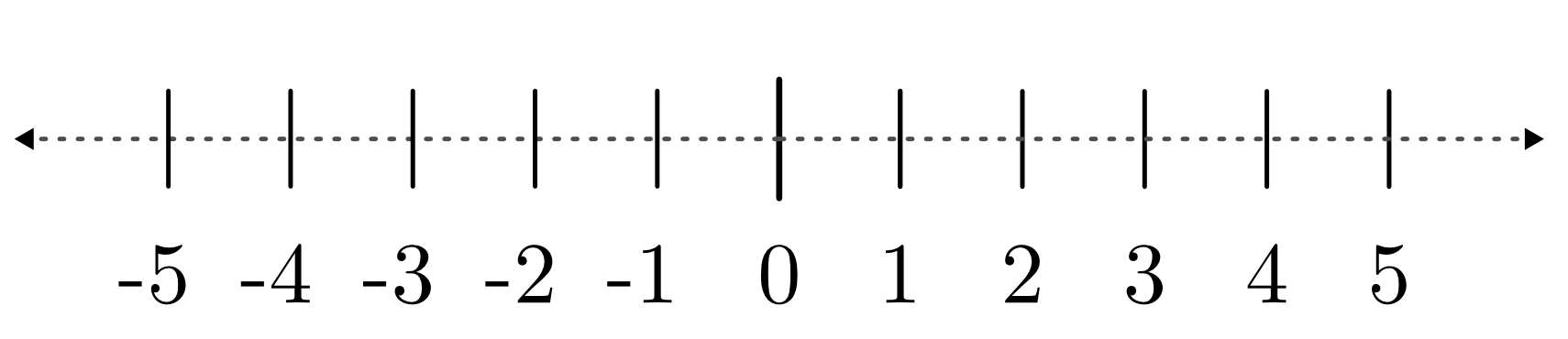
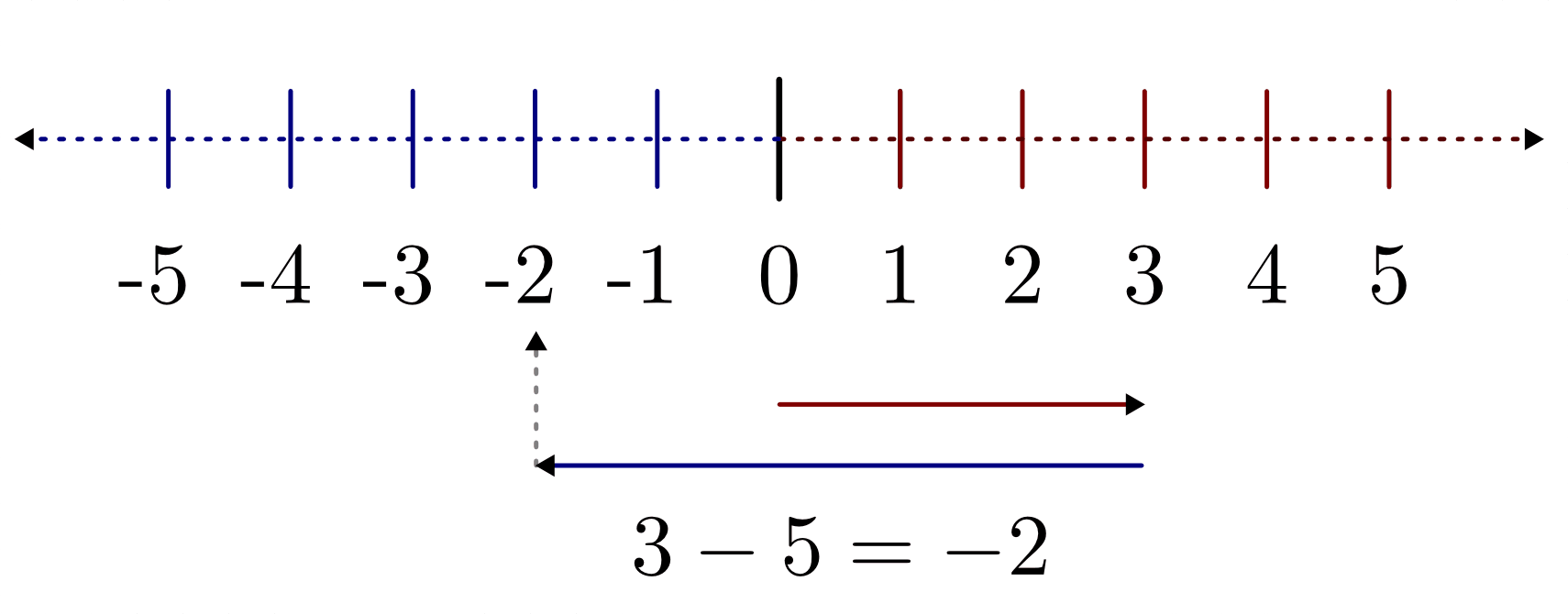

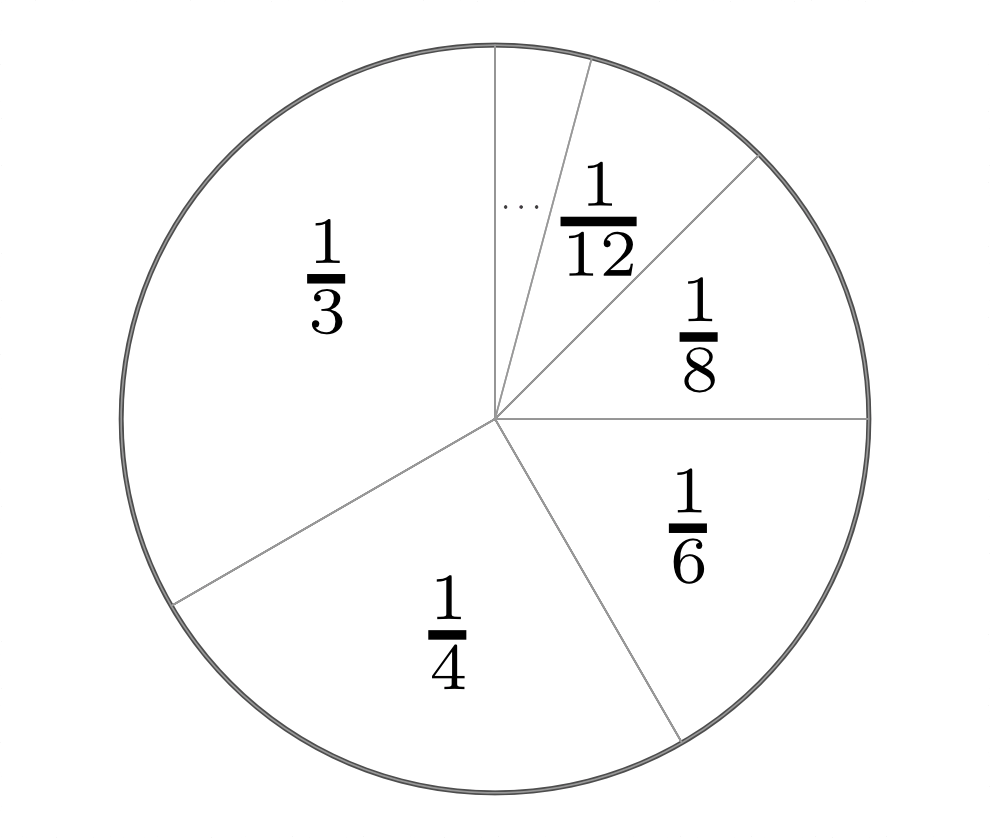
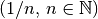 anhand
eines Tortendiagramms.
anhand
eines Tortendiagramms.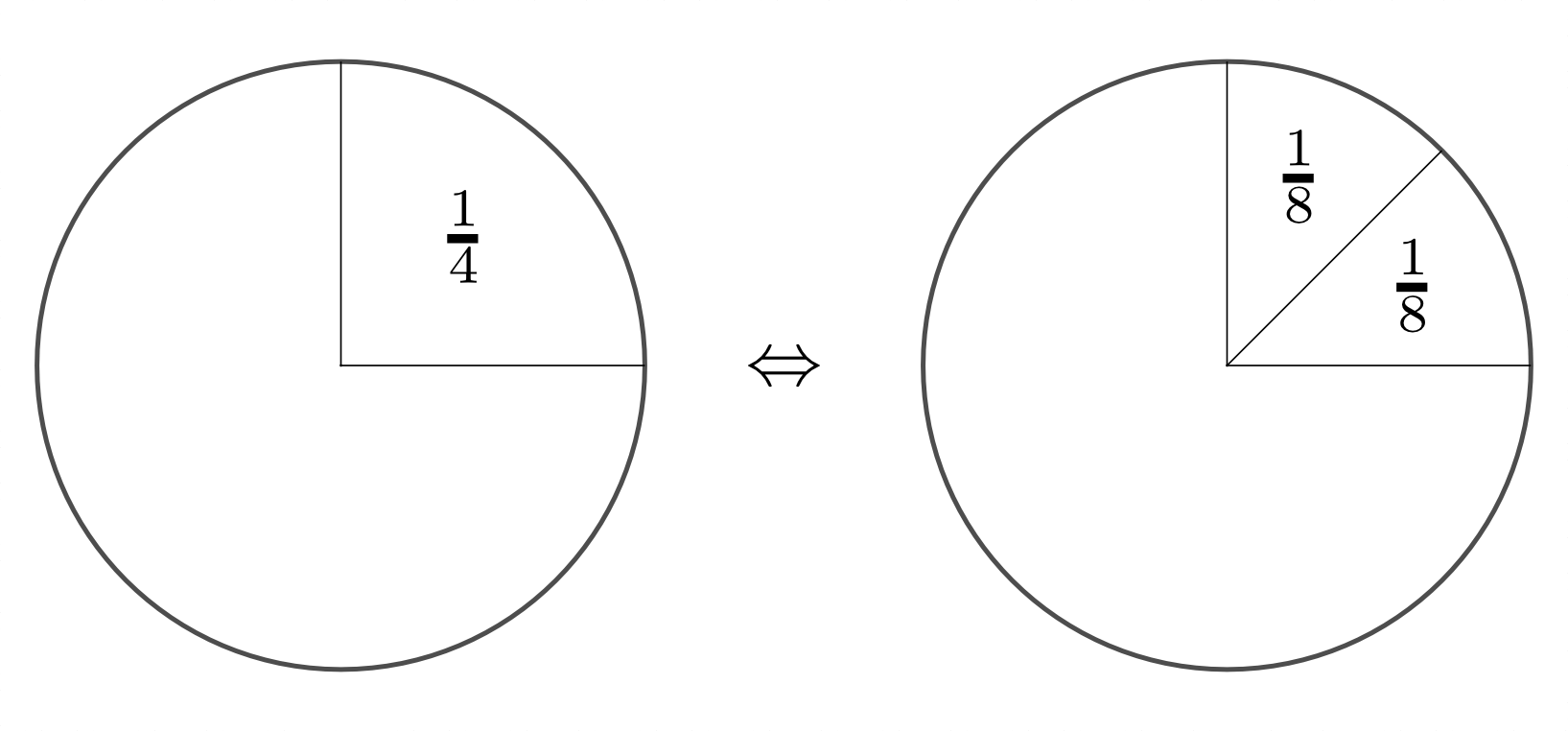
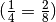 am Beispiel eines
Tortendiagramms.
am Beispiel eines
Tortendiagramms.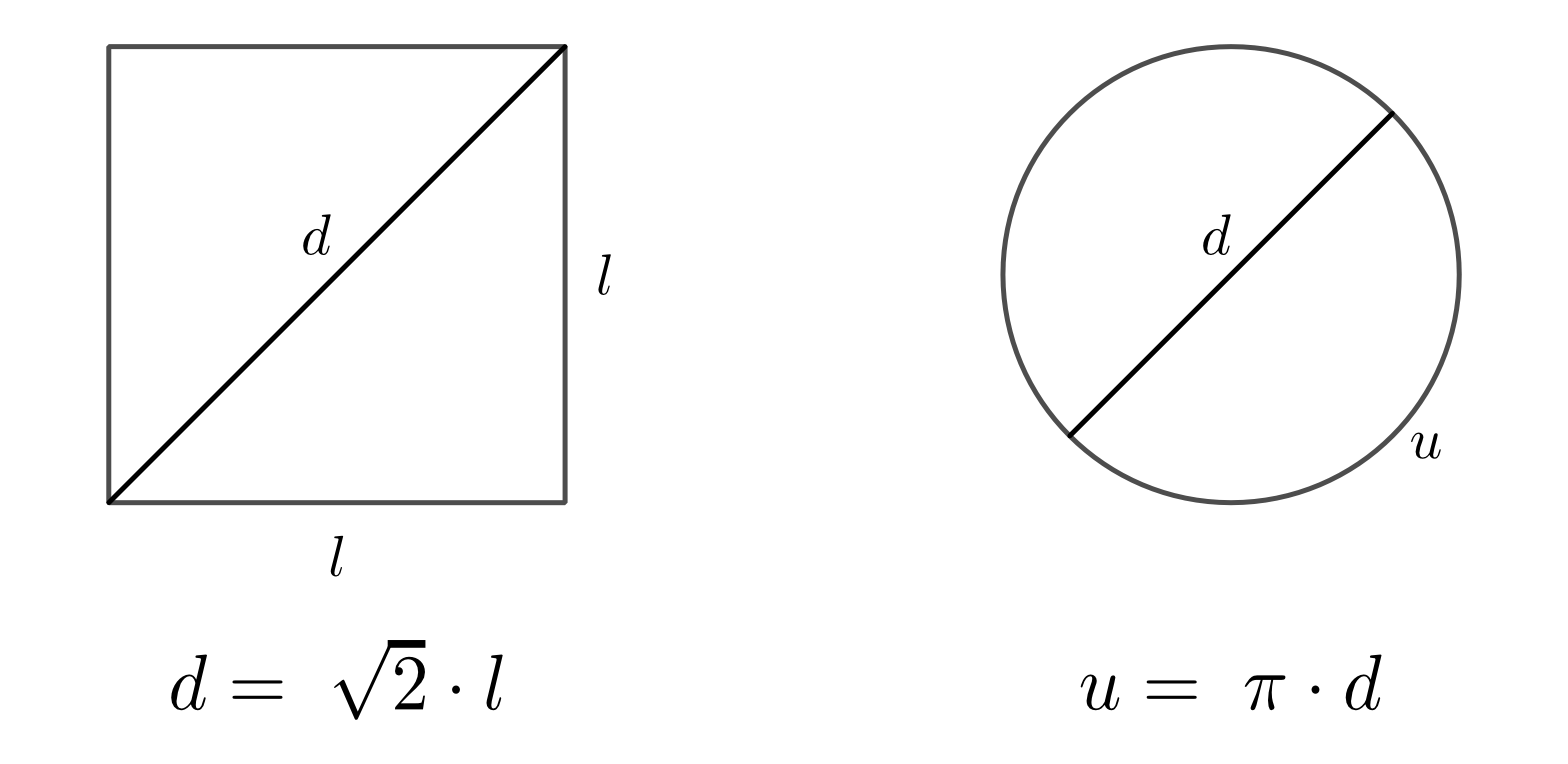
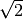 und
und  als irrationale
Zahlen.
als irrationale
Zahlen. ist grundsätzlich unmöglich:
ist grundsätzlich unmöglich: und
und
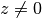 , so müsste ebenfalls
, so müsste ebenfalls 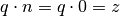 gelten. Es gilt jedoch für jede beliebige Zahl
gelten. Es gilt jedoch für jede beliebige Zahl 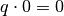 und
somit
und
somit 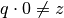 .
.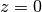 würde zwar
würde zwar 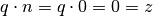 gelten. Hierbei wäre allerdings
gelten. Hierbei wäre allerdings 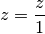
 des Nenners
des Nenners