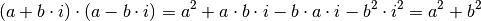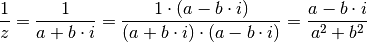Exkurs: Komplexe Zahlen¶
Die Menge der komplexen Zahlen 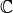 stellt eine zusätzliche
Erweiterung der reellen Zahlen dar. Ein ursprüngliches Ziel dieser Erweiterung
war es, auch die Rechenoperation des Wurzelziehens uneingeschränkt mit allen
Zahlen des zugrunde liegenden Zahlenbereichs ausführbar zu machen, also auch
Wurzeln mit negativen Argumenten zu definieren.
stellt eine zusätzliche
Erweiterung der reellen Zahlen dar. Ein ursprüngliches Ziel dieser Erweiterung
war es, auch die Rechenoperation des Wurzelziehens uneingeschränkt mit allen
Zahlen des zugrunde liegenden Zahlenbereichs ausführbar zu machen, also auch
Wurzeln mit negativen Argumenten zu definieren.
Um eine Lösung für eine Wurzel mit negativem Argument angeben zu können, wird
formal eine „imaginäre Einheit“  eingeführt, welche die folgende
Gleichung erfüllt:
eingeführt, welche die folgende
Gleichung erfüllt:
(1)¶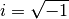
Die Menge  der imaginären Zahlen entspricht der Menge an
Zahlen, die man erhält, wenn man die imaginäre Einheit
der imaginären Zahlen entspricht der Menge an
Zahlen, die man erhält, wenn man die imaginäre Einheit  mit einem
beliebigen (reellen) Vielfachen
mit einem
beliebigen (reellen) Vielfachen 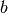 multipliziert:
multipliziert:
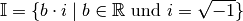
Bildet man die Summe aus einer reellen Zahl  und einer imaginären
Zahl
und einer imaginären
Zahl  , so erhält man eine komplexe Zahl
, so erhält man eine komplexe Zahl  :
:
(2)¶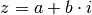
Für die Menge 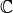 der komplexen Zahlen gilt entsprechend:
der komplexen Zahlen gilt entsprechend:
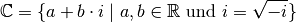
Jede komplexe Zahl  setzt sich somit aus einem „Realteil“
setzt sich somit aus einem „Realteil“  und
einem „Imaginärteil“
und
einem „Imaginärteil“  zusammen. Die Menge der reellen Zahlen
zusammen. Die Menge der reellen Zahlen
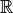 stellen dabei eine Teilmenge der komplexen Zahlen
stellen dabei eine Teilmenge der komplexen Zahlen
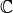 dar, für die
dar, für die 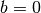 gilt.
gilt.
Rechnen mit komplexen Zahlen
Die Rechenregeln für reelle Zahlen lassen sich weitgehend auf komplexe Zahlen
übertragen, wenn man 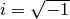 beziehungsweise die dazu äquivalente Beziehung
beziehungsweise die dazu äquivalente Beziehung
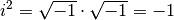 beachtet.
beachtet.
- Addiert beziehungsweise subtrahiert man zwei komplexe Zahlen
 und
und
 , so erhält man eine neue komplexe Zahl, deren Real- und
Imaginärteil gleich der Summe beziehungsweise Differenz der Real- und
Imaginärteile von
, so erhält man eine neue komplexe Zahl, deren Real- und
Imaginärteil gleich der Summe beziehungsweise Differenz der Real- und
Imaginärteile von 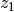 und
und 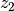 ist:
ist:
(3)¶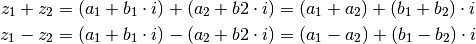
- Multipliziert man zwei komplexe Zahlen
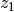 und
und 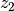 miteinander, so erhält man eine neue komplexe Zahl, indem man alle Komponenten
beider Zahlen miteinander multipliziert und hierbei
miteinander, so erhält man eine neue komplexe Zahl, indem man alle Komponenten
beider Zahlen miteinander multipliziert und hierbei 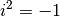 setzt.[1]
setzt.[1]
(4)¶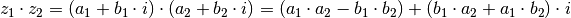
- Dividiert man eine komplexe Zahl
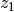 durch eine andere komplexe Zahl
durch eine andere komplexe Zahl
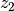 miteinander, so erhält man eine neue komplexe Zahl, indem man den
Bruch um die so genannte „komplex konjugierte“ Zahl
miteinander, so erhält man eine neue komplexe Zahl, indem man den
Bruch um die so genannte „komplex konjugierte“ Zahl  des Nenners erweitert:[2][3]
des Nenners erweitert:[2][3]
(5)¶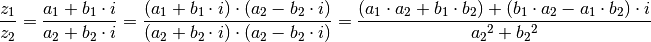
Gaußsche Zahlenebene und Polarform
Komplexe Zahlen lassen sich zwar nicht auf einer Zahlengeraden, dafür aber als Punkte einer Zahlenebene (zu Ehren von Carl Friedrich Gauss auch „Gauss’sche Ebene“ genannt) darstellen, die von einer reellen und dazu senkrecht stehenden imaginären Zahlenachse aufgespannt wird.
Eine komplexe Zahl lässt sich in der Gauss’schen Ebene entweder anhand ihrer
Koordinaten (Real- und Imaginärteil) oder anhand der Länge 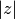 und
Richtung
und
Richtung 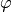 ihres Zeigers bestimmen. Die Länge des Zeigers, die
vom Koordinatenursprung zum Ort der Zahl führt, ist eine nicht negative reelle
Zahl:
ihres Zeigers bestimmen. Die Länge des Zeigers, die
vom Koordinatenursprung zum Ort der Zahl führt, ist eine nicht negative reelle
Zahl:
(6)¶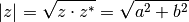
Hierbei wird wiederum genutzt, dass das Produkt einer komplexen Zahl 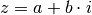 mit ihrer konjugiert komplexen Zahl
mit ihrer konjugiert komplexen Zahl 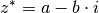 gleich der reellen Zahl
gleich der reellen Zahl 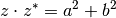 ist. In der
Gauss’schen Ebene kann die komplex konjugierte Zahl
ist. In der
Gauss’schen Ebene kann die komplex konjugierte Zahl 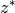 durch eine
vertikale Spiegelung von
durch eine
vertikale Spiegelung von  an der reellen Zahlenachse bestimmt werden.
an der reellen Zahlenachse bestimmt werden.
Der Zusammenhang zwischen dem Real- und Imaginärteil von  , ihrem Betrag
, ihrem Betrag
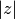 und dem Winkel
und dem Winkel 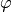 ihres Zeigers kann mittels der
trigonomischen Größen
ihres Zeigers kann mittels der
trigonomischen Größen 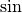 und
und  formuliert werden. Es
gilt:
formuliert werden. Es
gilt:

Jede komplexe Zahl kann somit neben der Koordinatenform auch in einer so
genannten „Polarform“, also über die Angabe ihres Betrags 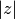 und
Winkels
und
Winkels 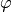 , in folgender Weise angegeben werden:
, in folgender Weise angegeben werden:

beziehungsweise
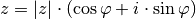
… to be continued …
Anmerkungen:
| [1] | Explizit kommt Gleichung (4) folgendermaßen zustande:
In der letzten Zeile wurde die Beziehung |
| [2] | Die Multiplikation einer komplexen Zahl
Hierbei wurde wiederum die Beziehung |
| [3] | Mit Hilfe der Divisionsformel (5) kann beispielsweise auch der Kehrbruch einer komplexen Zahl bestimmt werden. Es gilt:
|

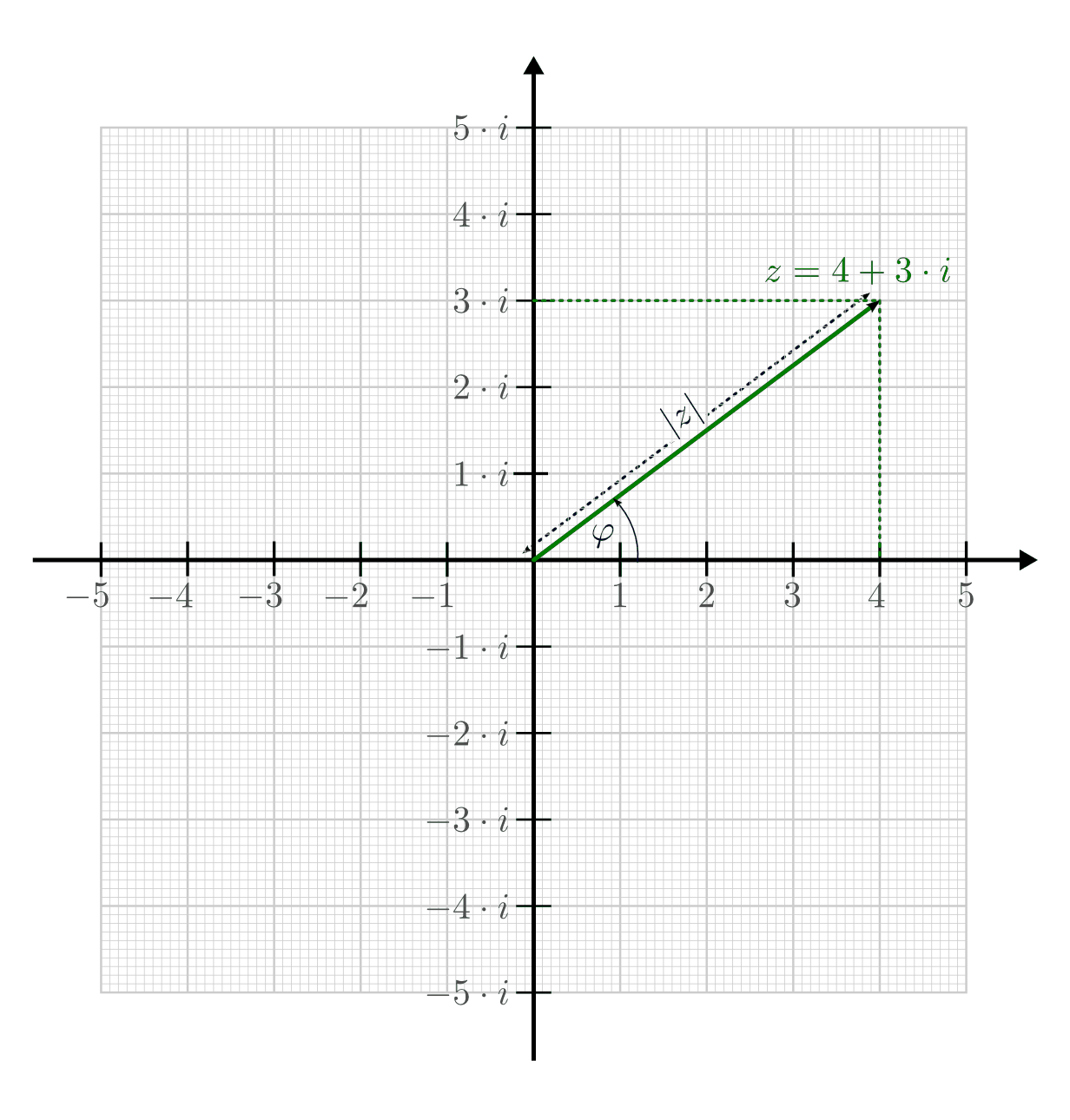
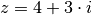 anhand der
Gauss’schen Zahlenebene.
anhand der
Gauss’schen Zahlenebene.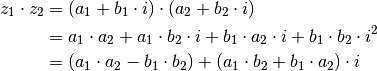
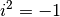 genutzt.
Zusätzlich wurden die bei der Multiplikation entstandenen realen und
imaginären Anteile sortiert und durch Klammern zusammen gefasst.
genutzt.
Zusätzlich wurden die bei der Multiplikation entstandenen realen und
imaginären Anteile sortiert und durch Klammern zusammen gefasst.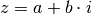 mit
ihrer komplex konjugierten Zahl
mit
ihrer komplex konjugierten Zahl  ergibt die
(reelle) Zahl
ergibt die
(reelle) Zahl 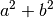 :
: