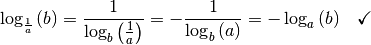Exponential- und Logarithmusfunktionen¶
Exponentialfunktionen¶
Exponentialfunktionen haben allgemein folgende Funktionsgleichung:
(1)¶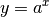
Dabei bezeichnet die „Basis“ 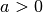 eine beliebige, konstante Zahl.
Üblicherweise wird zudem der Fall
eine beliebige, konstante Zahl.
Üblicherweise wird zudem der Fall 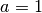 ausgeschlossen, da
ausgeschlossen, da 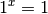 eine konstante Funktion liefert. Am weitesten verbreitet sind die
Exponentialfunktionen mit den Basen
eine konstante Funktion liefert. Am weitesten verbreitet sind die
Exponentialfunktionen mit den Basen 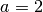 ,
,  und
und
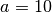 .[1]
.[1]
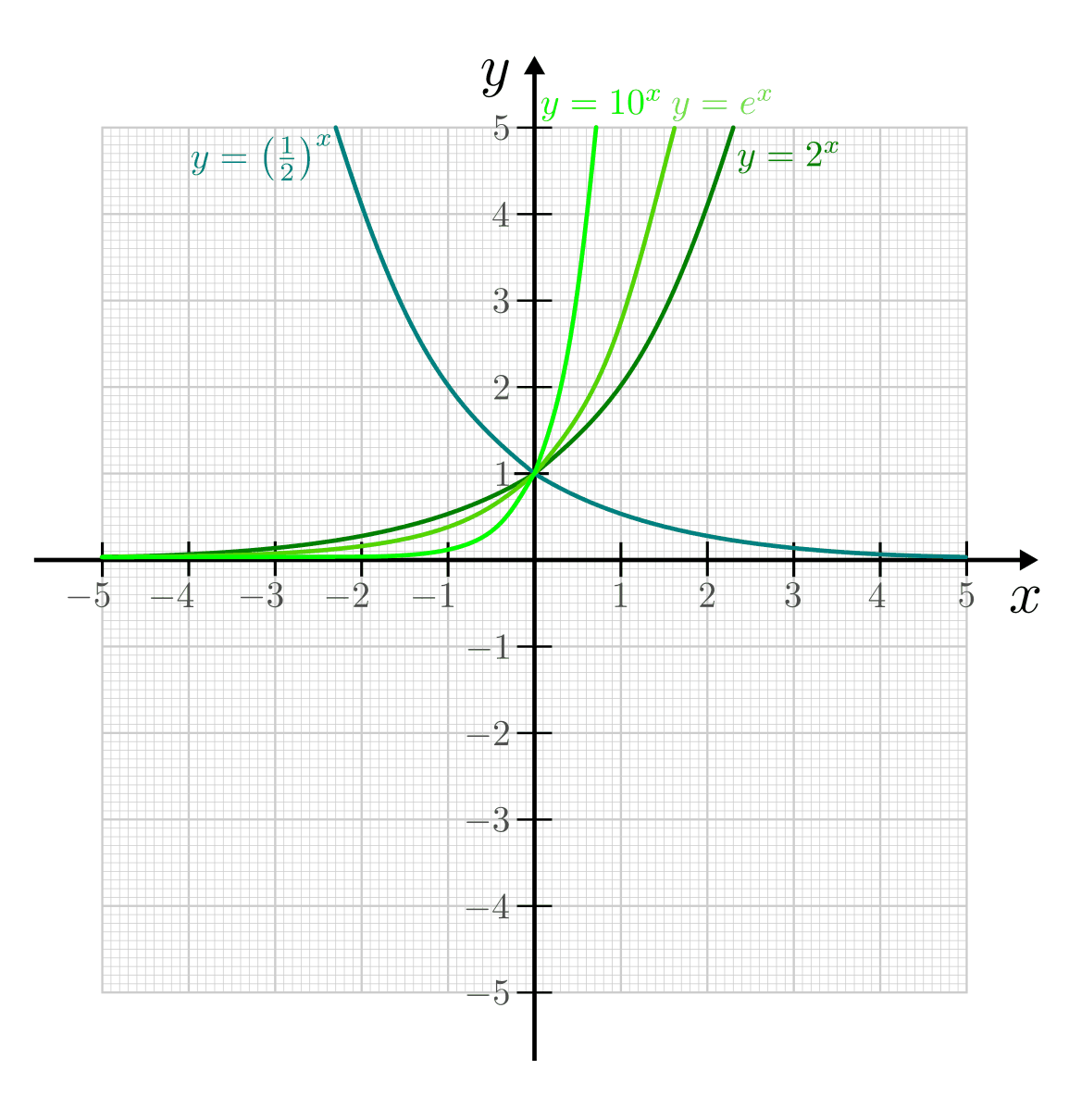
Im Fall 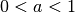 sind Exponentialfunktionen streng monoton fallend, im Fall
sind Exponentialfunktionen streng monoton fallend, im Fall
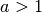 streng monoton steigend. Alle Exponentialfunktionen haben den Punkt
streng monoton steigend. Alle Exponentialfunktionen haben den Punkt
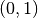 gemeinsam und nähern sich asymptotisch der
gemeinsam und nähern sich asymptotisch der  -Achse an,
ohne diese jemals zu berühren. Exponentialfunktionen haben somit keine
Nullstellen und
-Achse an,
ohne diese jemals zu berühren. Exponentialfunktionen haben somit keine
Nullstellen und 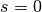 als untere Schranke.
Die Funktionen
als untere Schranke.
Die Funktionen 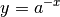 und
und 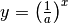 sind
identisch; ihr gemeinsamer Funktionsgraph verläuft bezüglich der
sind
identisch; ihr gemeinsamer Funktionsgraph verläuft bezüglich der  -Achse
symmetrisch zur Funktion
-Achse
symmetrisch zur Funktion 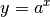 .[2]
.[2]
Für Exponentialfunktionen sind die folgenden vier Rechenregeln für Potenzen von Bedeutung:
(2)¶![a ^{x_1 + x_2} &= a ^{x_1} \cdot a ^{x_2} \\[4pt]
a ^{x_1 - x_2} &= a ^{x_1} : a ^{x_2} \\[4pt]
a ^{x_1 \;\cdot\, x_2} &= \left(a ^{x_1}\right)^{x_2} \\[4pt]
{\color{white}1 \qquad\qquad }a ^{\frac{x_1}{x_2}} &= \sqrt[x_2\;]{a ^{x_1}} \quad \;(\text{mit } x_2 \ne 0)](../../_images/math/c29245d077fdf01a5799f55a058cb6e5b15821fa.png)
Eine besondere Bedeutung von Exponentialfunktionen 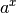 mit
mit 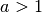 liegt darin, dass ihre Werte schneller wachsen als es bei einer Potenzfunktion
liegt darin, dass ihre Werte schneller wachsen als es bei einer Potenzfunktion
 mit beliebig großem (aber festem)
mit beliebig großem (aber festem)  der Fall ist; es gilt
also für beliebige Werte
der Fall ist; es gilt
also für beliebige Werte 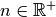 und
und 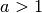 :
:
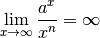
Der Grund dafür liegt darin, dass die Ableitung einer Exponentialfunktion als Maß für die Steigung der jeweiligen
Funktion selbst eine Exponentialfunktion ist: Nicht nur die Werte wachsen für
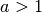 somit exponentiell an, sondern auch die Zunahme der Werte nimmt in
diesem Fall exponentiell zu.
somit exponentiell an, sondern auch die Zunahme der Werte nimmt in
diesem Fall exponentiell zu.
Logarithmusfunktionen¶
Logarithmusfunktionen sind die Umkehrfunktionen von Exponentialfunktionen. Sie haben allgemein folgende Funktionsgleichung:
(3)¶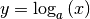
Da Exponentialfunktionen eindeutig umkehrbar sind, gibt es zu jeder
Exponentialfunktion eine entsprechende Logarithmusfunktion. Da der
Definitionsbereich jeder Umkehrfunktion gleich dem Wertebereich der
Originalfunktion ist, sind Logarithmen nur für 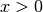 definiert.
definiert.
Logarithmusfunktionen sind nur für 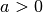 und
und 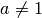 definiert.
Wie bei den Exponentialfunktionen, so sind auch bei den Logarithmusfunktionen
die Basen
definiert.
Wie bei den Exponentialfunktionen, so sind auch bei den Logarithmusfunktionen
die Basen 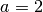 ,
,  und
und 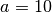 am weitesten verbreitet; sie
werden, wie bereits im Abschnitt Rechenregeln für Logarithmen beschrieben, als binärer, natürlicher und
dekadischer Logarithmus bezeichnet:
am weitesten verbreitet; sie
werden, wie bereits im Abschnitt Rechenregeln für Logarithmen beschrieben, als binärer, natürlicher und
dekadischer Logarithmus bezeichnet:

Im Fall 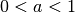 sind Logarithmusfunktionen streng monoton fallend, im
Fall
sind Logarithmusfunktionen streng monoton fallend, im
Fall 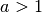 streng monoton steigend. Die einzelnen Logarithmusfunktionen
können jeweils durch einen Basiswechsel in einen Logarithmus mit einer anderen
Basis umgeformt werden. Es gilt dabei:
streng monoton steigend. Die einzelnen Logarithmusfunktionen
können jeweils durch einen Basiswechsel in einen Logarithmus mit einer anderen
Basis umgeformt werden. Es gilt dabei:
(4)¶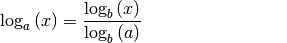
Alle Logarithmusfunktionen sind unbeschränkt, haben den Punkt 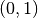 als
einzige Nullstelle gemeinsam und nähern sich für
als
einzige Nullstelle gemeinsam und nähern sich für 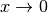 asymptotisch
der
asymptotisch
der  -Achse an. Die Funktionen
-Achse an. Die Funktionen  und
und
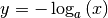 sind identisch; ihr gemeinsamer Funktionsgraph verläuft
bezüglich der
sind identisch; ihr gemeinsamer Funktionsgraph verläuft
bezüglich der  -Achse symmetrisch zur Funktion
-Achse symmetrisch zur Funktion 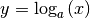 .[3]
.[3]
Für Logarithmusfunktionen sind die folgenden Rechenregeln von Bedeutung:
(5)¶![\log_{a}{(x_1 \cdot x_2)} &= \log_{a}{(x_1)} + \log_{a}{(x_2)} \\[4pt]
\log_{a}{(x_1 : x_2)} &= \log_{a}{(x_1)} - \log_{a}{(x_2)} \\[4pt]
\log_{a}{(x_1)^{x_2}} &= x_2 \cdot \log_{a}{(x_1)} \\[4pt]
\log_{a}{(\sqrt[x_2\;]{x_1})} &= \frac{1}{x_2} \cdot \log_{a}{(x_1)} \quad
\;(\text{mit } x_1,\, x_2 \ne 0)](../../_images/math/b39ffe90c642ae4a76eac95d59d4ad60b1c245af.png)
Eine besondere Bedeutung von Logarithmusfunktionen 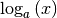 mit
mit
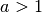 liegt darin, dass ihre Werte langsamer wachsen als es bei einer
Potenz- beziehungsweise Wurzelfunktion
liegt darin, dass ihre Werte langsamer wachsen als es bei einer
Potenz- beziehungsweise Wurzelfunktion  mit beliebig kleinem (aber festem)
mit beliebig kleinem (aber festem)
 der Fall ist; es gilt also für beliebige Werte
der Fall ist; es gilt also für beliebige Werte 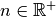 und
und 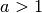 :
:
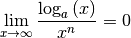
Der Grund dafür liegt darin, dass die Ableitung einer Logarithmusfunktion als Maß für die Steigung der jeweiligen
Funktion sehr schnell gegen Null geht; beispielsweise ist für 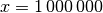 der Wert der Wurzelfunktion
der Wert der Wurzelfunktion 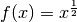 gleich
gleich
 , der Wert der Logarithmusfunktion
, der Wert der Logarithmusfunktion
 beträgt für diesen Wert hingegen nur
beträgt für diesen Wert hingegen nur
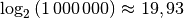 . Dennoch ist der Grenzwert für
. Dennoch ist der Grenzwert für
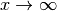 bei jeder Logarithmus-Funktion
bei jeder Logarithmus-Funktion  mit
mit 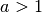 ebenfalls Unendlich.
ebenfalls Unendlich.
Anmerkungen:
| [1] | Dabei bezeichnet 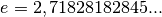 die „Eulersche Zahl“. die „Eulersche Zahl“. |
| [2] | Die Identität von 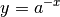 und und 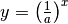 ergibt sich aus der Beziehung ergibt sich aus der Beziehung 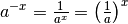 . . |
| [3] | Die Identität von
Insgesamt gilt somit:
|


 und
und 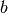 :
: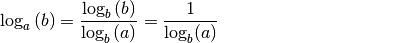
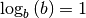 genutzt.
genutzt.
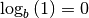 genutzt.
genutzt.