Ableitungen von Exponential- und Logarithmusfunktionen¶
Ableitungen von Exponentialfunktionen¶
Eine Ableitungsregel für Exponentialfunktionen
kann mit Hilfe des Differentialquotienten hergeleitet werden. Für eine Exponentialfunktion 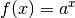 gilt:
gilt:
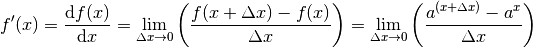
Mit Hilfe der Rechenregeln für Potenzen kann dieser Term weiter umgeformt werden. Es folgt:
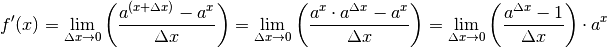
Die Ableitung einer Exponentialfunktion ist somit wieder eine
Exponentialfunktion, die mit einem konstanten, jedoch von der Basis  abhängigen Faktor multipliziert wird. Es lässt sich ein bestimmter Wert
abhängigen Faktor multipliziert wird. Es lässt sich ein bestimmter Wert
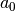 finden, für den der genannte Faktor gleich
finden, für den der genannte Faktor gleich 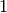 ist. Hierfür
muss gelten:
ist. Hierfür
muss gelten:

Dieser Grenzwert entspricht formal dem Grenzwert einer Folge 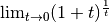 reeller Zahlen. Dieser Grenzwert konnte erstmals von
Leonhard Euler bestimmt
werden und wird zu dessen Ehren „Eulersche Zahl“
reeller Zahlen. Dieser Grenzwert konnte erstmals von
Leonhard Euler bestimmt
werden und wird zu dessen Ehren „Eulersche Zahl“  genannt:
genannt:

Diese Zahl ist irrational und für die Mathematik von ähnlicher Bedeutung wie
die Kreiszahl  : Ist nämlich die Eulersche Zahl
: Ist nämlich die Eulersche Zahl  Basis einer
Exponentialfunktion, ist also
Basis einer
Exponentialfunktion, ist also 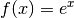 , so ist die Ableitungsfunktion
mit der ursprünglichen Funktion identisch, es gilt in diesem Fall also:
, so ist die Ableitungsfunktion
mit der ursprünglichen Funktion identisch, es gilt in diesem Fall also:
(1)¶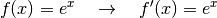
Die Funktion 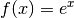 wird mitunter auch als „natürliche“
Exponentialfunktion bezeichnet.
wird mitunter auch als „natürliche“
Exponentialfunktion bezeichnet.
Für beliebige Exponentialfunktionen lässt sich eine Ableitungsregel herleiten,
indem man ausnutzt, dass Exponential- und Logarithmusfunktionen bei gleicher
Basis  zueinander Umkehrfunktionen sind, also beispielsweise
zueinander Umkehrfunktionen sind, also beispielsweise 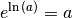 gilt. Für eine allgemeine Exponentialfunktion kann folglich
geschrieben werden:
gilt. Für eine allgemeine Exponentialfunktion kann folglich
geschrieben werden:
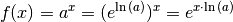
Um diese Funktion ableiten zu können, muss – wie schon im Abschnitt Ableitungen von Potenzfunktionen mit rationalem Exponenten die so genannte „Kettenregel“ genutzt werden:
Die Ableitung einer verketteten Funktion
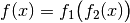 ist gleich der Ableitung der äußeren Funktion multipliziert mit der
Ableitung der inneren Funktion:
ist gleich der Ableitung der äußeren Funktion multipliziert mit der
Ableitung der inneren Funktion: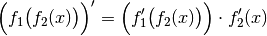
Beim Ableiten der äußeren Funktion wird die innere Funktion dabei unverändert gelassen.
Für die obige Gleichung 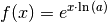 entspricht
entspricht
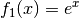 der äußeren und
der äußeren und 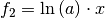 der
inneren Funktion. Da
der
inneren Funktion. Da 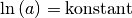 ist, gilt:[1]
ist, gilt:[1]

Die natürliche Exponentialfunktion als äußere Funktion bleibt hierbei
unverändert, die Ableitung der inneren Funktion 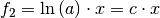 ergibt den Wert
ergibt den Wert 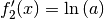 . Für
Exponentialfunktionen mit beliebiger Basis
. Für
Exponentialfunktionen mit beliebiger Basis  gilt also:
gilt also:
(2)¶
In dieser Formel ist wegen 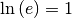 der Sonderfall für die natürliche
Exponentialfunktion enthalten.
der Sonderfall für die natürliche
Exponentialfunktion enthalten.
Ableitungen von Logarithmusfunktionen¶
Um eine Ableitungsregel für Logarithmusfunktionen herzuleiten, wird eine weitere, als „Umkehrregel“ bezeichnete Ableitungsregel verwendet:
Die Ableitung
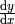 einer Funktion
einer Funktion
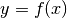 ist gleich dem Kehrwert der Ableitung ihrer Umkehrfunktion
ist gleich dem Kehrwert der Ableitung ihrer Umkehrfunktion
 :
: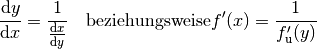
Im Fall einer Logarithmusfunktion ist  und, wenn
man beide Seiten als Potenz zur Basis
und, wenn
man beide Seiten als Potenz zur Basis  schreibt,
schreibt, 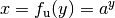 . Somit gilt nach der Ableitungsregel
(2) für Exponentialfunktionen:
. Somit gilt nach der Ableitungsregel
(2) für Exponentialfunktionen:
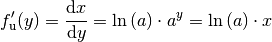
Für die Ableitung der Logarithmusfunktion gilt schließlich:
(3)¶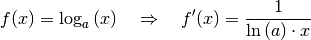
Im Sonderfall der natürlichen Logarithmusfunktion 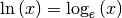 ist
ist 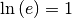 und somit:
und somit:
(4)¶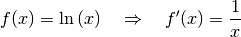
Alle weiteren Ableitungen der Logarithmusfunktion lassen sich dann gemäß den Ableitungsregeln für gebrochenrationalen Funktionen bestimmen.
Anmerkungen:
| [1] | Um sich die Wirkung der Kettenregel im Detail vorstellen zu können, kann
man an dieser Stelle auch 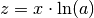 schreiben. Die äußere
Funktion ist dann schreiben. Die äußere
Funktion ist dann 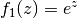 , deren Ableitung , deren Ableitung  ist. ist. |
