Ableitungen von ganz- und gebrochenrationalen Funktionen¶
Ableitungen von ganzrationalen Funktionen¶
Eine ganzrationale Funktion hat allgemein folgende Form:
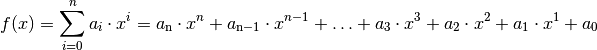
Um die Ableitung einer solchen Funktion zu bestimmen, müssen folgende zwei Ableitungsregeln verwendet werden:
Wird eine Funktion
 mit einem konstanten Faktor
mit einem konstanten Faktor  multipliziert, so bleibt dieser Faktor beim Ableiten unverändert erhalten.
Für die Ableitung gilt somit:
multipliziert, so bleibt dieser Faktor beim Ableiten unverändert erhalten.
Für die Ableitung gilt somit: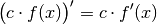
Ist
 negativ, so ist die Funktion gegenüber der ursprünglichen
Funktion an der
negativ, so ist die Funktion gegenüber der ursprünglichen
Funktion an der  -Achse gespiegelt. In diesem Fall hat auch die
Steigung ein umgekehrtes Vorzeichen.
-Achse gespiegelt. In diesem Fall hat auch die
Steigung ein umgekehrtes Vorzeichen.Besteht eine Funktion
 aus einer Summe von Einzelfunktionen
aus einer Summe von Einzelfunktionen
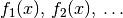 , so ist die Ableitung gleich der Summe der
Ableitungen der Einzelfunktion. Es gilt also:
, so ist die Ableitung gleich der Summe der
Ableitungen der Einzelfunktion. Es gilt also: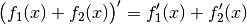
Mit den obigen Regeln und den Ableitungsregeln für Potenzfunktionen ergibt sich somit für die erste
Ableitung einer ganzrationalen Funktion  -ten Grades:
-ten Grades:
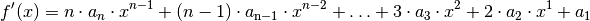
Die Ableitung einer ganzrationalen Funktion  -ten Grades ist somit eine
ganzrationale Funktion
-ten Grades ist somit eine
ganzrationale Funktion  -ten Grades. Leitet man die Funktion ein
zweites mal ab, so wird der Grad der Ableitungsfunktion wiederum um
-ten Grades. Leitet man die Funktion ein
zweites mal ab, so wird der Grad der Ableitungsfunktion wiederum um  niedriger. Für die zweite Ableitung gilt entsprechend:
niedriger. Für die zweite Ableitung gilt entsprechend:

Insgesamt lässt sich eine ganzrationale Funktion  -ten Grades also
-ten Grades also
 mal ableiten; alle weiteren Ableitungen sind gleich Null.
mal ableiten; alle weiteren Ableitungen sind gleich Null.
Ableitungen von gebrochenrationalen Funktionen¶
Eine gebrochenrationale Funktion hat allgemein folgende Form:
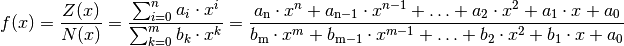
Gebrochenrationale Funktionen bestehen also aus einem Zählerpolynom  mit Grad
mit Grad  und einem Nennerpolynom
und einem Nennerpolynom  mit Grad
mit Grad 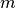 ; die
Grade des Zählerpolynoms und des Nennerpolynoms unterscheiden sich also um
; die
Grade des Zählerpolynoms und des Nennerpolynoms unterscheiden sich also um
 . Um eine solche Funktion ableiten zu können, muss eine weitere
Ableitungsregel verwendet werden:
. Um eine solche Funktion ableiten zu können, muss eine weitere
Ableitungsregel verwendet werden:
Besteht eine Funktion
 aus einem Quotienten zweier
Einzelfunktionen
aus einem Quotienten zweier
Einzelfunktionen 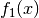 und
und  , so lässt sich die
Ableitung von
, so lässt sich die
Ableitung von  nach folgender Regel berechnen:
nach folgender Regel berechnen: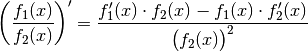
Für die Ableitung einer gebrochenrationalen Funktion gilt also:
(1)¶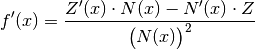
Die Ableitungen des Zähler- bzw. Nennerpolynoms werden dabei gemäß den Regeln
für Ableitungen ganzrationaler Funktionen gebildet. Das Ergebnis ist hierbei
wiederum eine gebrochenrationale Funktion, wobei sich die Grade des
Zählerpolynoms und des Nennerpolynoms der Ableitung um 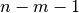 unterscheiden.
unterscheiden.
Echt gebrochen-rationale Funktionen mit 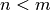 lassen sich somit
unbegrenzt oft ableiten, wobei die einzelnen Ableitungen niemals gleich Null
sind.
lassen sich somit
unbegrenzt oft ableiten, wobei die einzelnen Ableitungen niemals gleich Null
sind.
Ableitungen von Hyperbelfunktionen
Hyperbeln, also Funktionen der Form 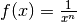 , sind der einfachste Sonderfall von gebrochenrationalen
Funktionen. Für ihre Ableitung gilt:
, sind der einfachste Sonderfall von gebrochenrationalen
Funktionen. Für ihre Ableitung gilt:
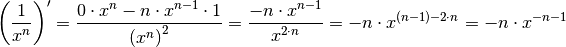
Schreibt man für die Hyperbelfunktion  ,
so zeigt sich, dass die Ableitungen entsprechend der Ableitungsregel für
Potenzfunktionen gebildet werden
können:
,
so zeigt sich, dass die Ableitungen entsprechend der Ableitungsregel für
Potenzfunktionen gebildet werden
können:
(2)¶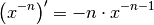
Die Ableitungsregel für Potenzfunktionen gilt also nicht nur für positive
rationale Werte von  , sondern allgemein für negative ganzzahlige Werte
von
, sondern allgemein für negative ganzzahlige Werte
von  .
.
Ableitungen von Potenzfunktionen mit rationalem Exponenten
Um zu zeigen, dass die Ableitungsregel für Potenzfunktionen allgemein für
jede rationale Zahl 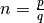 mit
mit 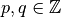 gilt, muss eine weitere Ableitungsregel verwendet werden:
gilt, muss eine weitere Ableitungsregel verwendet werden:
Besteht eine Funktion
 aus einer Verkettung zweier
Einzelfunktionen
aus einer Verkettung zweier
Einzelfunktionen 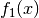 und
und  , so lässt sich die Ableitung von
, so lässt sich die Ableitung von  nach
der so genannten „Kettenregel“ berechnen:
nach
der so genannten „Kettenregel“ berechnen: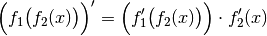
Dabei wird zunächst die äußere Funktion abgeleitet, die innere Funktion bleibt dabei unverändert. Anschließend wird der sich ergebende Term mit der Ableitung der inneren Funktion multipliziert.
Für die Ableitung einer Potenzfunktion 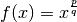 mit
rationalem Exponenten
mit
rationalem Exponenten 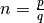 gilt damit:
gilt damit:
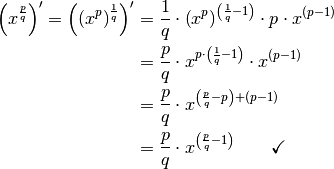
Hierbei werden die Rechenregeln für Potenzen und Wurzeln genutzt und  als „äußere“
sowie
als „äußere“
sowie 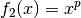 als „innere“ Funktion interpretiert. Beim Ableiten der
äußeren Funktion bleibt die innere Funktion als eigener Term unverändert. Das
Ergebnis wird anschließend mit der Ableitung der inneren Funktion multipliziert,
was umgangssprachlich als „Nachdifferenzieren“ bezeichnet wird. Ein
Zusammenfassen der einzelnen Terme führt schließlich zum gesuchten Endergebnis.
als „innere“ Funktion interpretiert. Beim Ableiten der
äußeren Funktion bleibt die innere Funktion als eigener Term unverändert. Das
Ergebnis wird anschließend mit der Ableitung der inneren Funktion multipliziert,
was umgangssprachlich als „Nachdifferenzieren“ bezeichnet wird. Ein
Zusammenfassen der einzelnen Terme führt schließlich zum gesuchten Endergebnis.
