Ableitungen von Potenz- und Wurzelfunktionen¶
Allgemein können Potenz- und Wurzelfunktionen in der Form 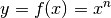 dargestellt werden, wobei
dargestellt werden, wobei
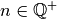 eine beliebige positive rationale Zahl ist. Diese
Funktionen sind an allen Stellen ihres Definitionsbereichs differenzierbar, da
bei Ableitungen von Hyperbelfunktionen ihre Steigung entweder gleich bleibt oder
sich kontinuierlich ändert.[1] Es lässt sich somit jeweils eine Funktion
eine beliebige positive rationale Zahl ist. Diese
Funktionen sind an allen Stellen ihres Definitionsbereichs differenzierbar, da
bei Ableitungen von Hyperbelfunktionen ihre Steigung entweder gleich bleibt oder
sich kontinuierlich ändert.[1] Es lässt sich somit jeweils eine Funktion
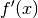 finden, die für jeden Wert
finden, die für jeden Wert  des Definitionsbereichs
genau den Wert der Steigung von
des Definitionsbereichs
genau den Wert der Steigung von  als Funktionswert liefert. Eine
solche Funktion
als Funktionswert liefert. Eine
solche Funktion 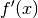 wird Ableitungsfunktion oder kurz Ableitung von
wird Ableitungsfunktion oder kurz Ableitung von
 genannt.
genannt.
Steigung und erste Ableitung¶
Die erste Ableitung 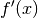 einer Funktion gibt an, wie schnell sich ihre
Funktionswerte ändern; man spricht auch von der „Steigung“ von
einer Funktion gibt an, wie schnell sich ihre
Funktionswerte ändern; man spricht auch von der „Steigung“ von  . Für
eine Potenzfunktion lässt sich die zugehörige Ableitung einfach nach folgender
Regel bestimmen:[2]
. Für
eine Potenzfunktion lässt sich die zugehörige Ableitung einfach nach folgender
Regel bestimmen:[2]
(1)¶
Die Ableitung einer Potenzfunktion ist somit wieder eine Potenzfunktion, deren
Grad um 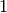 geringer ist als die ursprüngliche Funktion.
geringer ist als die ursprüngliche Funktion.
Beispiele:
Für
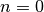 gilt
gilt 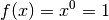 . Diese Funktion liefert für alle
. Diese Funktion liefert für alle
 -Werte konstant den Wert
-Werte konstant den Wert 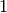 , die Funktionswerte ändern sich
also nicht. Die Steigung muss in diesem Fall also gleich Null sein. Nach der
obigen Regel wird diese Bedingung erfüllt:
, die Funktionswerte ändern sich
also nicht. Die Steigung muss in diesem Fall also gleich Null sein. Nach der
obigen Regel wird diese Bedingung erfüllt:(2)¶
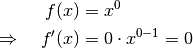
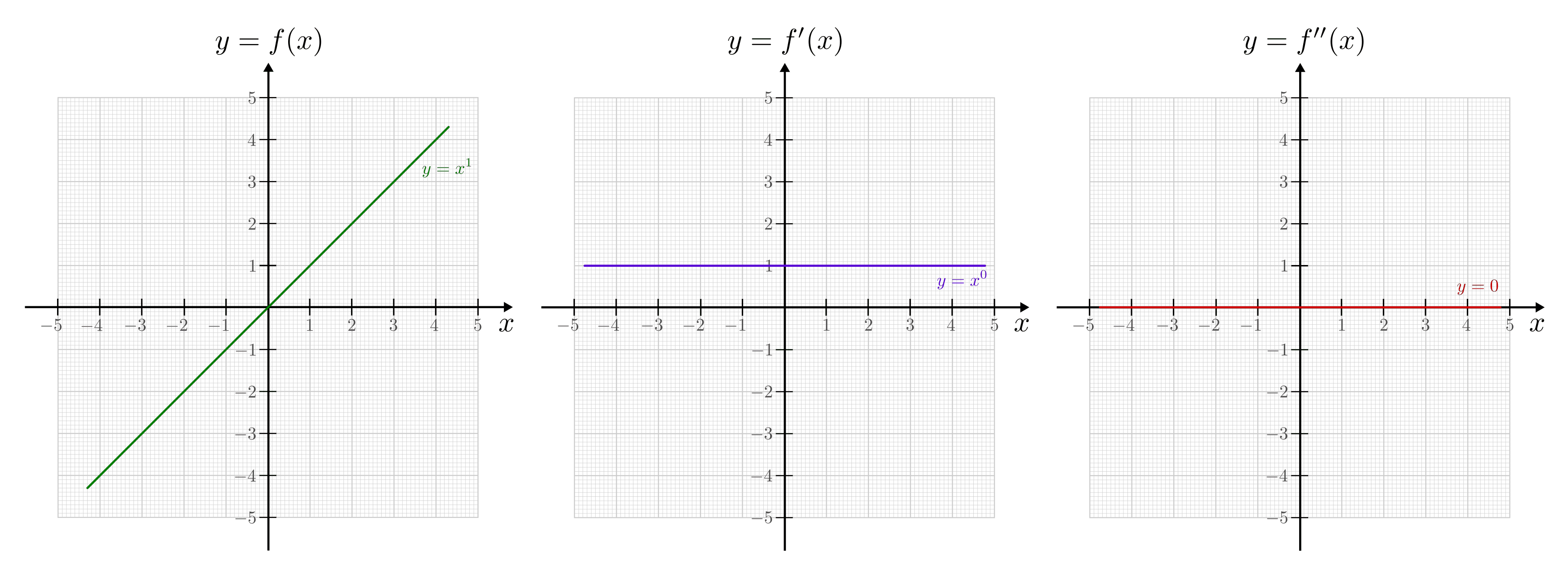
Für
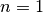 entspricht
entspricht  der Ursprungsgeraden
der Ursprungsgeraden
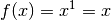 . Für die Ableitungsfunktion ergibt sich nach Gleichung
(1):
. Für die Ableitungsfunktion ergibt sich nach Gleichung
(1):![f(x) &= x^1 \\[6pt]
\Rightarrow f'(x) &= 1 \cdot x ^{1-1} = 1 \cdot x^0 = 1](../../_images/math/7ec16bfaf159e87eab9f34bd20ec324c1fe6f040.png)
Da eine Gerade stets eine konstante Steigung besitzt, liefert ihre Ableitungsfunktion für alle
 einen konstanten Wert. Dieser Wert ist
umso größer, je steiler die Gerade verläuft, und negativ, falls es sich um
eine fallende Gerade handelt.
einen konstanten Wert. Dieser Wert ist
umso größer, je steiler die Gerade verläuft, und negativ, falls es sich um
eine fallende Gerade handelt.Für
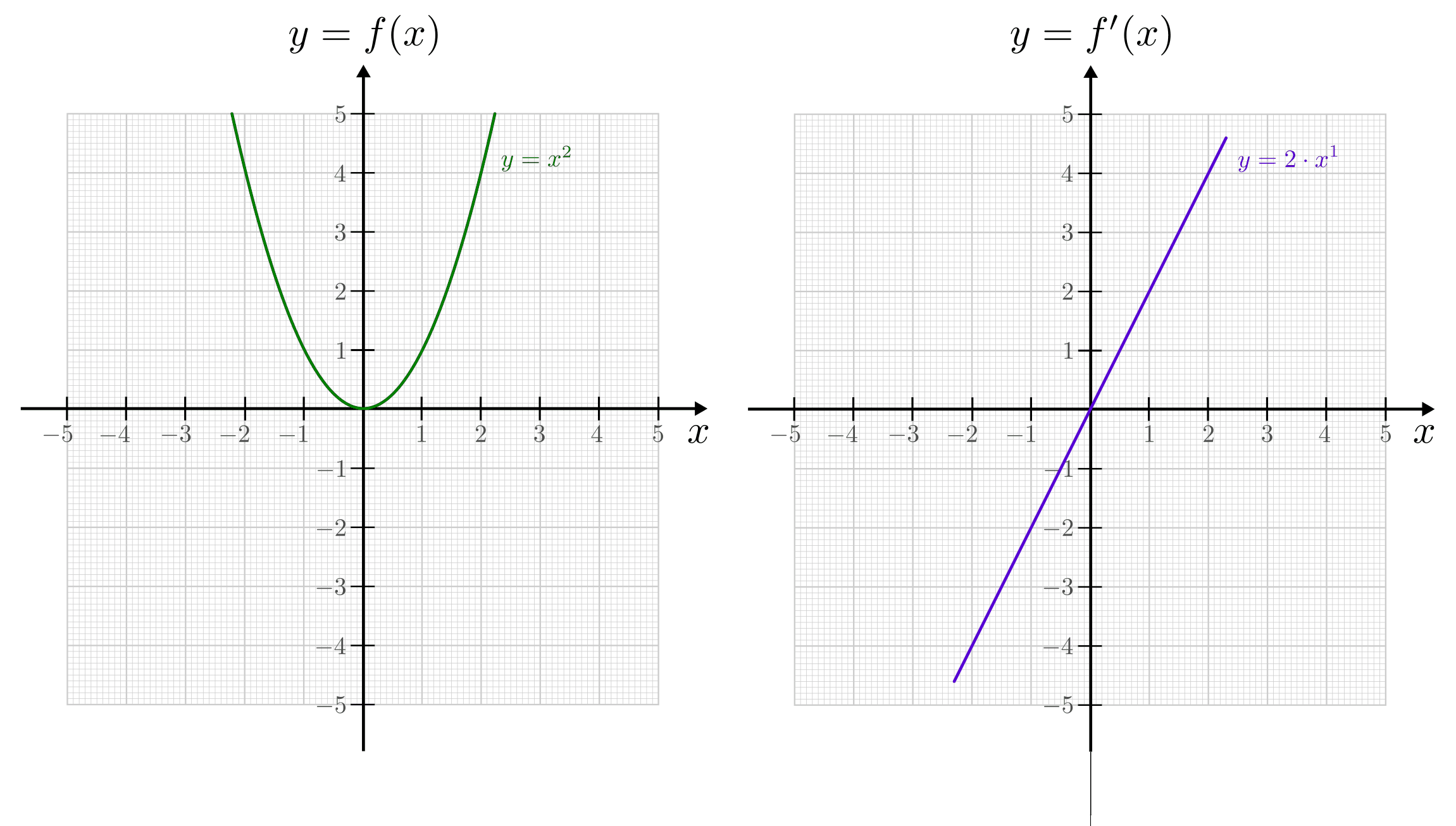
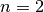 entspricht
entspricht  der Normalparabel
der Normalparabel 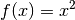 . Für die Ableitungsfunktion ergibt sich nach Gleichung
(1):
. Für die Ableitungsfunktion ergibt sich nach Gleichung
(1):![f(x) &= x^2 \\[6pt]
\Rightarrow f'(x) &= 2 \cdot x ^{2-1} = 2 \cdot x^1 = 2 \cdot x](../../_images/math/6dc91d4b9dd5228df3d1618909d0038017d35ffd.png)
Die Steigung der Normalparabel nimmt also konstant zu – von stark negativen Werten links der
 -Achse (der Graph der Ableitungsfunktion befindet
sich im negativen Wertebereich) bis hin zu stark positiven Werten rechts der
-Achse (der Graph der Ableitungsfunktion befindet
sich im negativen Wertebereich) bis hin zu stark positiven Werten rechts der
 -Achse.
-Achse.Für
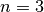 gilt
gilt 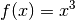 , und für die Ableitungsfunktion:
, und für die Ableitungsfunktion:![f(x) &= x^3 \\[6pt]
\Rightarrow f'(x) &= 3 \cdot x ^{3-1} = 3 \cdot x^2](../../_images/math/fd9f2a9af1e899d1090c8f06f7270a146dc2bedd.png)
Die Ableitungsfunktion
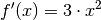 befindet sich stets im
positiven Wertebereich, was bedeutet, dass die Steigung der kubischen Funktion
befindet sich stets im
positiven Wertebereich, was bedeutet, dass die Steigung der kubischen Funktion
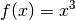 stets positiv (bzw. Null am Punkt
stets positiv (bzw. Null am Punkt 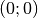 ) ist.
) ist.Für
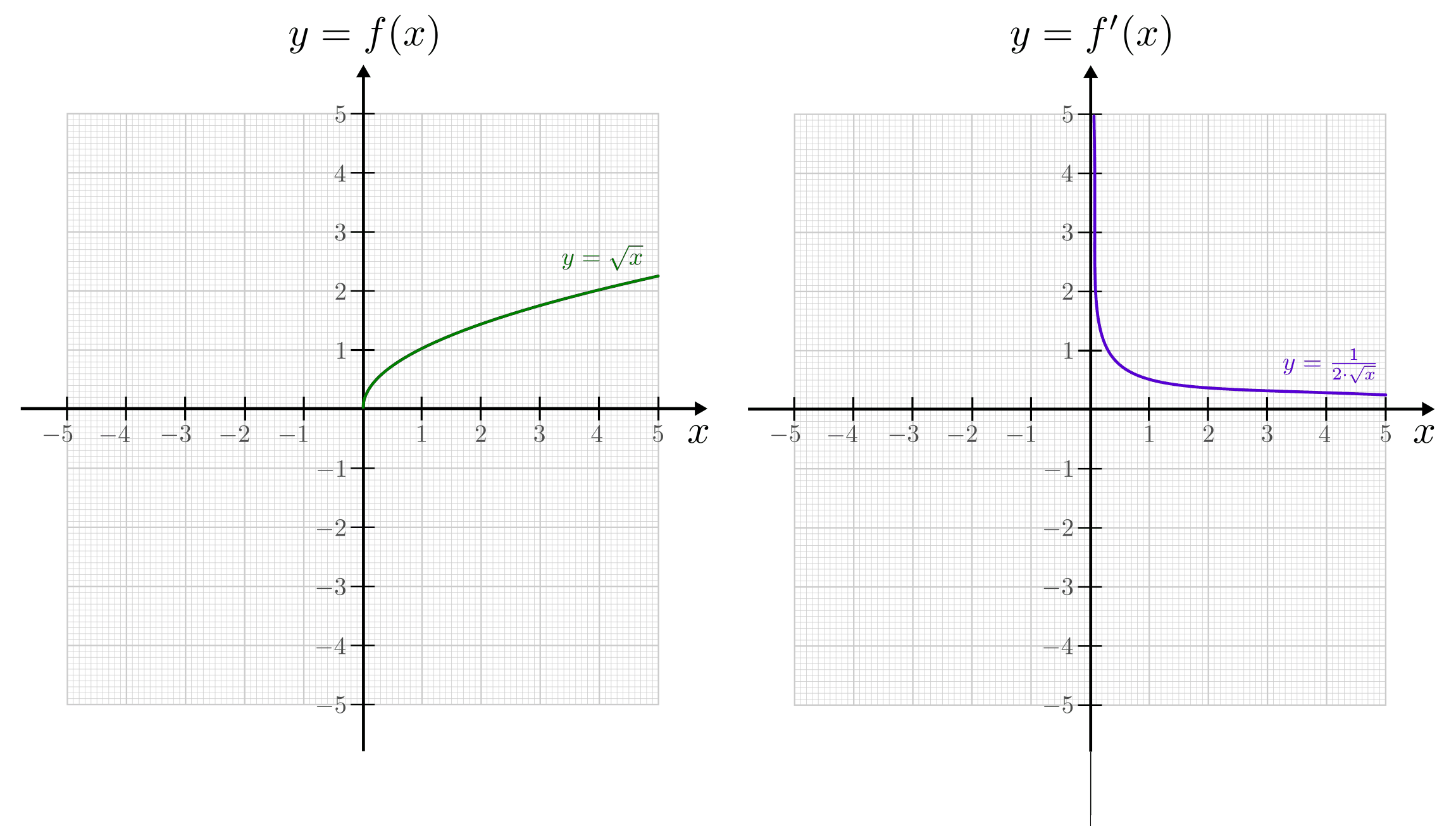
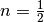 entspricht
entspricht 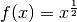 nach den
Rechenregeln für Wurzeln und Potenzen der Wurzelfunktion
nach den
Rechenregeln für Wurzeln und Potenzen der Wurzelfunktion 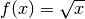 . Für die und
für die Ableitungsfunktion
. Für die und
für die Ableitungsfunktion 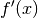 gilt in diesem Fall:
gilt in diesem Fall:![f(x) & = x ^{\frac{1}{2}} = \sqrt{x}\\[6pt]
\Rightarrow f'(x) &= \frac{1}{2} \cdot \left(x ^{\left(\frac{1}{2} -1\right)}\right)= \frac{1}{2}
\cdot \left(x ^{- \frac{1}{2}}\right) = \frac{1}{2} \cdot \left(\frac{1}{x ^{\frac{1}{2}}}\right) =
\frac{1}{2} \cdot \left(\frac{1}{\sqrt{x}}\right) = \frac{1}{2 \cdot \sqrt{x}}](../../_images/math/9b25efbdeb80a9aad586d0b8d1db9ffffd6b1b42.png)
Die Ableitungsfunktion
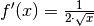 befindet
sich ebenfalls stets im positiven Wertebereich, da die Wurzelfunktion
befindet
sich ebenfalls stets im positiven Wertebereich, da die Wurzelfunktion
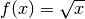 kontinuierlich wächst. Die Werte der
Ableitungsfunktion werden jedoch immer geringer, das heißt die Wurzelfunktion
wächst zunehmend langsamer.
kontinuierlich wächst. Die Werte der
Ableitungsfunktion werden jedoch immer geringer, das heißt die Wurzelfunktion
wächst zunehmend langsamer.
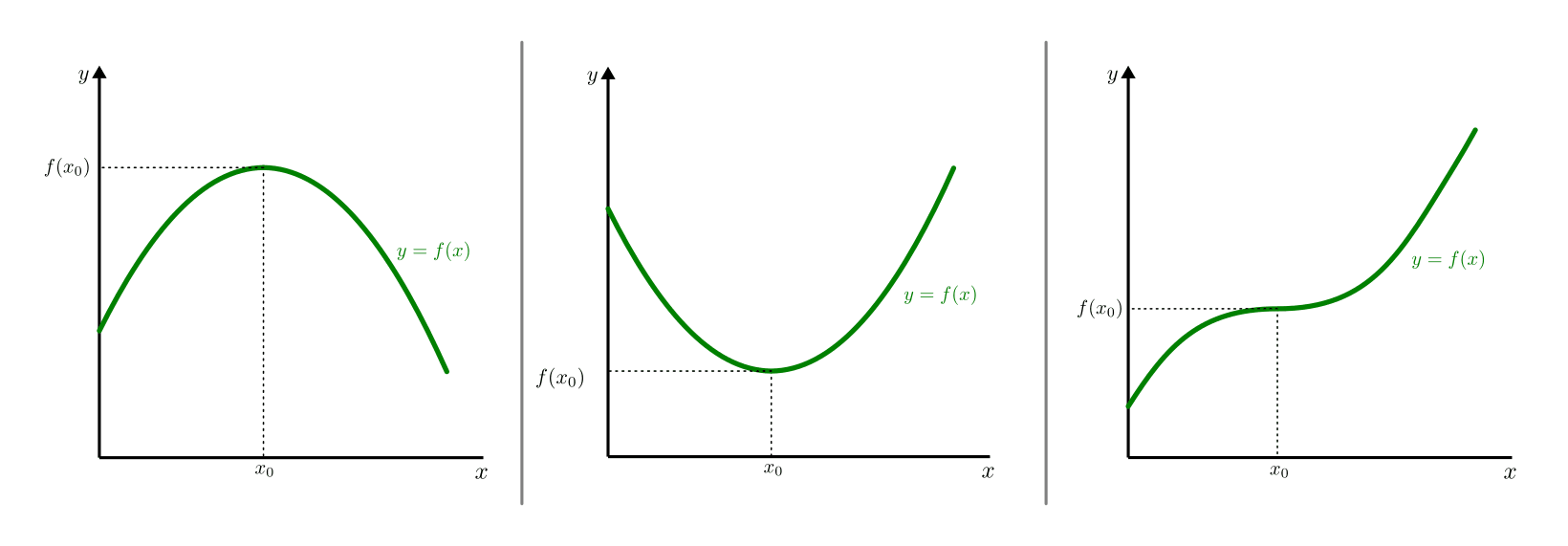
Die erste Ableitung kann genutzt werden, um differenzierbare Funktionen auf maximale und/oder minimale Funktionswerte hin zu untersuchen.
Extremstellen
Hat eine Funktion an einer Stelle  ein lokales Maximum („Hochpunkt“)
oder Minimum („Tiefpunkt“), so ist an dieser Stelle die Steigung der Funktion
und somit auch die erste Ableitung gleich Null. Der Wert der ersten Ableitung an
einer Stelle
ein lokales Maximum („Hochpunkt“)
oder Minimum („Tiefpunkt“), so ist an dieser Stelle die Steigung der Funktion
und somit auch die erste Ableitung gleich Null. Der Wert der ersten Ableitung an
einer Stelle  ist ebenfalls dann gleich Null, wenn die zugehörige
Funktion an dieser Stelle einen so genannten „Terrassenpunkt“ besitzt. In allen
drei Fällen spricht man von Extremstellen, die zugehörigen Funktionswerte von
ist ebenfalls dann gleich Null, wenn die zugehörige
Funktion an dieser Stelle einen so genannten „Terrassenpunkt“ besitzt. In allen
drei Fällen spricht man von Extremstellen, die zugehörigen Funktionswerte von
 werden Extremwerte genannt.
werden Extremwerte genannt.
Um die Extremstelle(n) einer differenzierbaren Funktion zu finden, genügt es
somit, die erste Ableitung zu berechnen und diese gleich Null zu setzen. Löst
man die zugehörige Gleichung, so erhält man die  -Werte von allen
Extremstellen. Um zu prüfen, ob es sich bei einer Extremstelle um einen
Hochpunkt, einen Tiefpunkt oder einen Terrassenpunkt handelt, kann man
folgende Fälle prüfen:
-Werte von allen
Extremstellen. Um zu prüfen, ob es sich bei einer Extremstelle um einen
Hochpunkt, einen Tiefpunkt oder einen Terrassenpunkt handelt, kann man
folgende Fälle prüfen:
- Vor einem Hochpunkt ist die erste Ableitung (Steigung) der Funktion zunächst positiv, nach dem Hochpunkt negativ.
- Vor einem Tiefpunkt ist die erste Ableitung (Steigung) der Funktion zunächst negativ, nach dem Tiefpunkt positiv.
- Vor und nach einem Terrassenpunkt ist die erste Ableitung der Funktion entweder jeweils positiv oder jeweils negativ.
Es genügt also, zu einer gefundenen Extremstelle  einen Wert
einen Wert
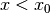 und einen Wert
und einen Wert 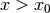 in die erste Ableitungsfunktion
einzusetzen und die Vorzeichen der jeweiligen Ergebnisse zu prüfen. Auf diese
Weise untergliedert man letztlich den Definitionsbereich in so genannte
Monotoniebereiche, also Bereiche, in denen die Steigung das gleiche Vorzeichen
hat. Man kann hierfür auch eine Tabelle mit den einzelnen Abschnitten als
Spalten anlegen und dort die Steigungs-Vorzeichen der einzelnen Abschnitte
eintragen. Auch daran kann man die Extremwerte unmittelbar ablesen.
in die erste Ableitungsfunktion
einzusetzen und die Vorzeichen der jeweiligen Ergebnisse zu prüfen. Auf diese
Weise untergliedert man letztlich den Definitionsbereich in so genannte
Monotoniebereiche, also Bereiche, in denen die Steigung das gleiche Vorzeichen
hat. Man kann hierfür auch eine Tabelle mit den einzelnen Abschnitten als
Spalten anlegen und dort die Steigungs-Vorzeichen der einzelnen Abschnitte
eintragen. Auch daran kann man die Extremwerte unmittelbar ablesen.
Bisweilen werden auch die einzelnen Hoch- bzw. Tiefpunkte untereinander verglichen. Der Hochpunkt mit dem größten Funktionswert und der Tiefpunkt mit dem niedrigsten Funktionswert werden absolute Extremstellen genannt, weitere Hoch- und Tiefpunkte bezeichnet man als lokale Extremstellen.
Krümmung und zweite Ableitung¶
Will man nicht nur wissen, welche Steigung eine Funktion an einer bestimmten
Stelle aufweist, sondern ist auch daran interessiert, wie schnell sich die
Steigung der Funktion ändert, so kann die erste Ableitung erneut abgeleitet
werden. Auf diese Weise erhält man die zweite Ableitung 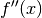 der
ursprünglichen Funktion. Sie gibt an, wie schnell sich die Steigungswerte der
Funktion ändern; die Änderung der Steigung wird als „Krümmung“ des Graphen
bezeichnet.
der
ursprünglichen Funktion. Sie gibt an, wie schnell sich die Steigungswerte der
Funktion ändern; die Änderung der Steigung wird als „Krümmung“ des Graphen
bezeichnet.
Stellt man sich ein Fahrzeug vor, das – von oben betrachtet – auf dem Graphen
der Funktion in Richtung zunehmender  -Werte entlangfährt, so gibt das
„Lenkverhalten“ des Fahrzeugs Aufschluss über die Krümmung der Funktion.
-Werte entlangfährt, so gibt das
„Lenkverhalten“ des Fahrzeugs Aufschluss über die Krümmung der Funktion.
- Legt das Fahrzeug auf seinem Weg entlang des Graphen eine Linkskurve zurück, so bezeichnet man die Krümmung der Funktion als positiv.
- Legt das Fahrzeug auf seinem Weg entlang des Graphen eine Rechtskurve zurück, so bezeichnet man die Krümmung der Funktion als negativ.
- Kann das Fahrzeug entlang des Graphen ohne zu lenken „geradeaus“ fahren, so ist die Krümmung des Graphen gleich Null.
In verschiedenen Bereichen der Funktion kann die Krümmung unterschiedlich sein.
Als anschauliche Beispiele eignen sich ebenfalls die einfachen Potenzfunktionen
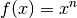 .
.
Beispiele:
Für
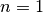 entspricht
entspricht  der Ursprungsgeraden
der Ursprungsgeraden 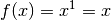 . Für die 1. Ableitung
. Für die 1. Ableitung 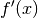 sowie für die 2. Ableitung
sowie für die 2. Ableitung
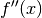 ergibt sich mit den Gleichungen
(1): und
(2):
ergibt sich mit den Gleichungen
(1): und
(2):![y = f(x) &= x^1 \\[6pt]
\Rightarrow f'(x) &= 1 = \text{konst.} \\[6pt]
\Rightarrow f''(x)&= 0](../../_images/math/e7d76e1894da49a110a6ea89f453d6c472683dc6.png)
Da die Steigung einer Geraden an allen Stellen gleich ist, tritt keine Krümmung auf: Der Wert der zweiten Ableitung ist – unabhängig vom eingesetzten
 -Wert – stets gleich Null.
-Wert – stets gleich Null.Für
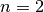 entspricht
entspricht  der Normalparabel
der Normalparabel 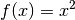 . Für die 1. Ableitung
. Für die 1. Ableitung 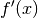 sowie für die 2. Ableitung
sowie für die 2. Ableitung
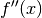 ergibt sich entsprechend:
ergibt sich entsprechend:![y = f(x) &= x^2 \\[6pt]
\Rightarrow f'(x) &= 2 \cdot x ^1 \\[6pt]
\Rightarrow f''(x) &= 2 \cdot x^0 = 2](../../_images/math/1815f5853c0663dc0399da4af7d86fb73590e362.png)
Eine Parabel besitzt stets eine konstante Krümmung. Im obigen Beispiel ist die Parabel nach oben geöffnet, ihre Krümmung ist positiv. (Ein Fahrzeug müsste – von oben betrachtet – entlang der Parabel eine Linkskurve fahren.)
Für
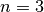 gilt
gilt 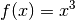 , und für die Ableitungsfunktionen nach
Gleichung (1):
, und für die Ableitungsfunktionen nach
Gleichung (1):![f(x) &= x^3 \\[6pt]
\Rightarrow f'(x) &= 3 \cdot x^2 \\[6pt]
\Rightarrow f''(x) &= 3 \cdot 2 \cdot x^1 = 6 \cdot x](../../_images/math/b1e106d8c164f56d087856f65b93d78b590631fd.png)
Die zweite Ableitung
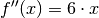 ist links der
ist links der  -Achse
negativ, was der negativen Krümmung der Funktion in diesem Bereich entspricht.
Am Punkt
-Achse
negativ, was der negativen Krümmung der Funktion in diesem Bereich entspricht.
Am Punkt 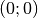 ist die zweite Ableitung gleich Null, an dieser Stelle
hat die Funktion keine Krümmung. Im Bereich rechts der
ist die zweite Ableitung gleich Null, an dieser Stelle
hat die Funktion keine Krümmung. Im Bereich rechts der  -Achse ist
die zweite Ableitung positiv, was einer Linkskrümmung des Funktionsgraphen
entspricht.
-Achse ist
die zweite Ableitung positiv, was einer Linkskrümmung des Funktionsgraphen
entspricht.
Extremstellen und zweite Ableitung
Hat man die zweite Ableitung einer Funktion berechnet, so kann auch diese
zur Klassifizierung von Extremstellen genutzt werden. Hierzu genügt es, den
gefundenen Wert  einer Extremstelle in die zweite Ableitung
einzusetzen:
einer Extremstelle in die zweite Ableitung
einzusetzen:
- Hat das Ergebnis ein positives Vorzeichen, so hat die Funktion an dieser Stelle einen Tiefpunkt.
- Hat das Ergebnis im umgekehrten Fall ein positives Vorzeichen, so hat die Funktion an dieser Stelle einen Hochpunkt.
- Ist das Ergebnis gleich Null, so hat die Funktion an dieser Stelle einen Terrassenpunkt.
Zur Veranschaulichung dieser Zusammenhänge können als elementare Beispiele
wiederum die Graphen der Funktionen 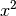 und
und 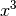 und ihrer
Ableitungen betrachtet werden.
und ihrer
Ableitungen betrachtet werden.
Beispiele:
- Die Funktion
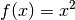 hat an der Stelle
hat an der Stelle 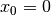 eine
Extremstelle; der Wert ihrer zweiten Ableitung
eine
Extremstelle; der Wert ihrer zweiten Ableitung  an dieser
Stelle ist
an dieser
Stelle ist  , es muss sich somit um einen Tiefpunkt handeln.
, es muss sich somit um einen Tiefpunkt handeln. - Die Funktion
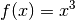 hat an der Stelle
hat an der Stelle 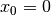 eine
Extremstelle; der Wert ihrer zweiten Ableitung
eine
Extremstelle; der Wert ihrer zweiten Ableitung 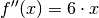 an
dieser Stelle ist
an
dieser Stelle ist 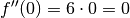 , es muss sich somit um einen
Terrassenpunkt handeln.
, es muss sich somit um einen
Terrassenpunkt handeln.
Die Methode, die Art der Extremstellen mittels der zweiten Ableitung zu
bestimmen, ist gegenüber der oben genannten Methode effizienter, da nur einmal
ein  -Wert in eine Funktion eingesetzt und der zugehörige Funktionswert
berechnet werden muss.
-Wert in eine Funktion eingesetzt und der zugehörige Funktionswert
berechnet werden muss.
Wendepunkte
Ändert sich an einer Stelle  die Krümmung einer Funktion, so ist an
dieser Stelle die zweite Ableitung gleich Null. Diese Bedingung kann genutzt
werden, um so genannte Wendepunkte einer Funktion zu bestimmen.
die Krümmung einer Funktion, so ist an
dieser Stelle die zweite Ableitung gleich Null. Diese Bedingung kann genutzt
werden, um so genannte Wendepunkte einer Funktion zu bestimmen.
Um Wendepunkte einer differenzierbaren Funktion zu finden, genügt es somit, die
zweite Ableitung zu berechnen und diese gleich Null zu setzen. Löst man die
zugehörige Gleichung, so erhält man die  -Werte aller möglicher
Wendepunkte; durch Einsetzen der
-Werte aller möglicher
Wendepunkte; durch Einsetzen der  -Werte in die ursprüngliche Funktion
erhält man die zugehörigen
-Werte in die ursprüngliche Funktion
erhält man die zugehörigen  -Werte. Es muss allerdings – ähnlich wie
bei Extremstellen – geprüft werden, ob es sich bei den
jeweiligen Stellen tatsächlich um Wendepunkte der Funktion handelt:
-Werte. Es muss allerdings – ähnlich wie
bei Extremstellen – geprüft werden, ob es sich bei den
jeweiligen Stellen tatsächlich um Wendepunkte der Funktion handelt:
- Ist die zweite Ableitung (Krümmung) einer Funktion zunächst negativ und anschließend positiv oder umgekehrt, so handelt es sich um einen Wendepunkt.
- Hat die zweite Ableitung (Krümmung) einer Funktion sowohl vor als auch nach
einer Stelle
 das gleiche Vorzeichen, so ist diese Stelle kein
Wendepunkt.
das gleiche Vorzeichen, so ist diese Stelle kein
Wendepunkt.
Es genügt also, zu einer gefundenen Nullstelle  der zweiten Ableitung
einen Wert
der zweiten Ableitung
einen Wert 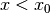 und einen Wert
und einen Wert 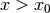 in die zweite
Ableitungsfunktion einzusetzen und die Vorzeichen der jeweiligen Ergebnisse zu
prüfen.[3]
in die zweite
Ableitungsfunktion einzusetzen und die Vorzeichen der jeweiligen Ergebnisse zu
prüfen.[3]
Anmerkung:
| [1] | Diese Regel lässt sich mit Hilfe des Differentialquotienten und der allgemeinen binomischen
Formel herleiten. Für
Die beiden
Geht in diesem Term |
| [2] | Dies ist gleichbedeutend damit, dass die Graphen keine „Knicke“ besitzen, vgl. Abschnitt Differenzierbarkeit.) |
| [3] | Sofern die dritte Ableitung der Funktion bereits berechnet
wurde, kann auch diese genutzt werden, um zu überprüfen, ob es sich bei
einer Stelle Ist die dritte Ableitung an der untersuchten Stelle |


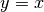 .
.
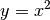 .
.
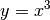 .
.
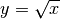 .
.


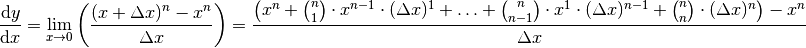
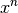 -Terme heben sich dabei aufgrund des
unterschiedlichen Vorzeichens auf. Alle verbleibenden Zählerterme enthalten
-Terme heben sich dabei aufgrund des
unterschiedlichen Vorzeichens auf. Alle verbleibenden Zählerterme enthalten
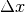 als Faktor, so dass dieser ausgeklammert und gekürzt werden
kann. Mit dem
als Faktor, so dass dieser ausgeklammert und gekürzt werden
kann. Mit dem  folgt:
folgt: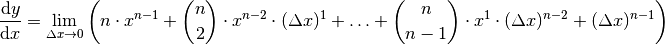
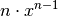 vernachlässigbar klein. Das Ergebnis entspricht somit der obigen
Ableitungsregel für Potenzfunktionen.
vernachlässigbar klein. Das Ergebnis entspricht somit der obigen
Ableitungsregel für Potenzfunktionen.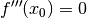 ,
so kann ein Wendepunkt jedoch nicht ausgeschlossen werden! Die oben genannte
Methode ist also für die Bestimmung von Wendepunkten zu bevorzugen.
,
so kann ein Wendepunkt jedoch nicht ausgeschlossen werden! Die oben genannte
Methode ist also für die Bestimmung von Wendepunkten zu bevorzugen.