Differenzen und Differentiale¶
Das Steigungsdreieck¶
Um die Bedeutung der Steigung einer Funktion zu verstehen, wird zunächst die Steigung einer Geraden betrachtet. Ein anschauliches Beispiel bietet eine Holzleiste oder ein Lineal, das schräg auf einer geraden Unterlage aufgestellt wird.
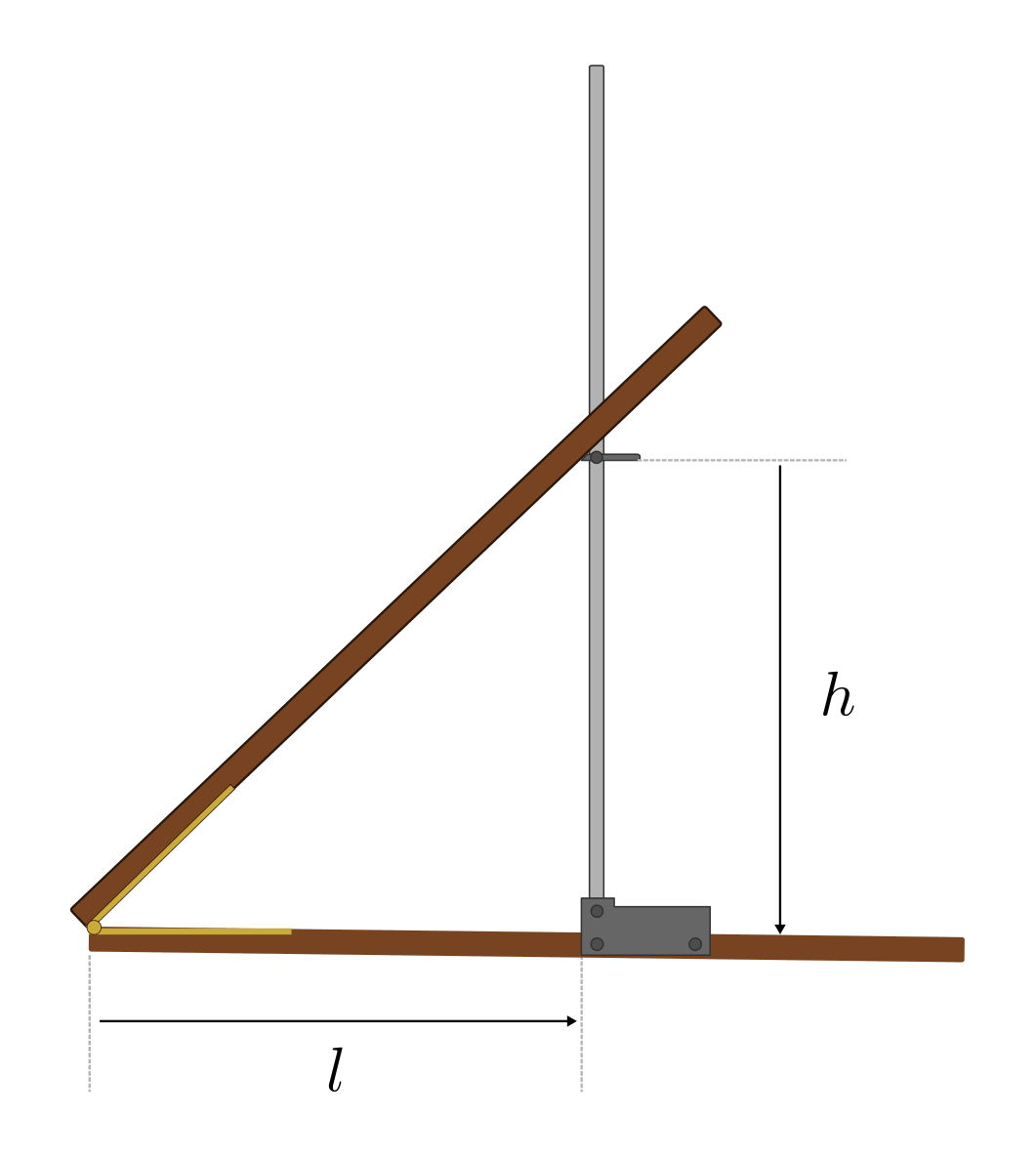
Modell eines Steigungsdreiecks. Durch Messen der Höhe  und Länge
und Länge
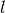 kann die Steigung einer schrägen Holzleiste bestimmt werden.
kann die Steigung einer schrägen Holzleiste bestimmt werden.
Umso schneller die Höhe  entlang der horizontalen Wegstrecke
entlang der horizontalen Wegstrecke 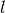 zunimmt, d.h. umso steiler das Lineal aufgestellt ist, desto größer ist die
Steigung.
zunimmt, d.h. umso steiler das Lineal aufgestellt ist, desto größer ist die
Steigung.
Ein solches „Steigungsdreieck“ kann in einem gewöhnlichen Koordinatensystem an jede Gerade angelegt werden. Wandert man von einem (frei wählbaren) Punkt auf der Geraden beispielsweise fünf Kästchen horizontal nach rechts und zählt dann die Anzahl an Kästchen, die man horizontal nach oben oder unten zurücklegen muss um wieder auf die Gerade zu treffen, so hat man ein Maß für die Steigung der Gerade gewonnen.
Beispiele:
- Eine Gerade, die entlang einer horizontalen Strecke von fünf Kästchen nach rechts um drei Kästchen nach oben ansteigt, ist weniger steil als eine Gerade, die entlang der gleichen horizontalen Strecke (fünf Kästchen) um sieben Kästchen nach oben steigt.
- Eine Gerade, die entlang einer horizontalen Strecke von drei Kästchen nach rechts um vier Kästchen nach oben ansteigt, ist steiler als eine Gerade, die entlang der gleichen horizontalen Strecke (drei Kästchen) um zwei Kästchen nach oben steigt.
- Eine Gerade, die entlang einer horizontalen Strecke von vier Kästchen nach rechts um acht Kästchen nach oben ansteigt, ist genauso steil wie eine Gerade, die entlang einer horizontalen Strecke von sechs Kästchen um zwölf Kästchen nach oben steigt.
Mathematisch kann das Verhältnis zwischen der vertikalen Änderung  und der horizontalen Änderung
und der horizontalen Änderung 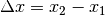 als
Bruch geschrieben werden:
als
Bruch geschrieben werden:
(1)¶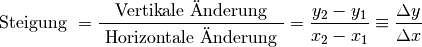
Da die beiden Änderungsgrößen 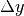 und
und 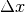 die gleiche
Einheit (z.B. Kästchen oder cm) besitzen, besitzt die Steigung keine Einheit.
die gleiche
Einheit (z.B. Kästchen oder cm) besitzen, besitzt die Steigung keine Einheit.
- Der Wert der Steigung ist positiv, wenn mit zunehmenden
 -Werten die
zugehörigen
-Werten die
zugehörigen  -Werte größer werden.
-Werte größer werden. - Die Steigung ist gleich Null, wenn mit zunehmenden
 -Werten die
zugehörigen
-Werten die
zugehörigen  -Werte unverändert (konstant) bleiben.
-Werte unverändert (konstant) bleiben. - Eine negative Steigung bedeutet entsprechend, dass mit zunehmenden
 -Werten die zugehörigen
-Werten die zugehörigen  -Werte kleiner werden.
-Werte kleiner werden.

Das Verkehrszeichen weist auf einen Berg mit einer (durchschnittlichen) Steigung von 12 Prozent hin.
Die Steigung kann auch in Prozent angegeben werden. Eine Steigung von 100%
bedeutet beispielsweise, dass die Gerade mit jedem Kästchen nach rechts um genau
ein Kästchen nach oben steigt. Da jedes Steigungsdreiecks rechtwinklig ist, kann
für beliebige Steigungen kann der Steigungswinkel 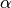 mit Hilfe der
trigonometrischen Beziehung
mit Hilfe der
trigonometrischen Beziehung  berechnet werden:
berechnet werden:
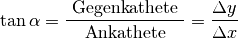
Eine Steigung von 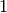 oder
oder 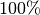 bedeutet gerade, dass je
horizontaler Wegdifferenz
bedeutet gerade, dass je
horizontaler Wegdifferenz 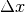 eine ebenso große vertikale
Wegdifferenz
eine ebenso große vertikale
Wegdifferenz 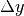 vorliegt; dies ist genau dann der Fall, wenn
vorliegt; dies ist genau dann der Fall, wenn
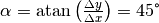 ist.
ist.
Differenzen- und Differentialquotient¶
Die meisten Funktionen haben keine einheitliche Steigung. Vielmehr nimmt die Steigung an verschiedenen Stellen unterschiedliche Werte an, kann mitunter in unterschiedlichen Bereichen auch das Vorzeichen wechseln.
Um die durchschnittliche Steigung einer beliebigen Funktion 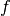 in einen
bestimmten Bereich zwischen einem Startwert
in einen
bestimmten Bereich zwischen einem Startwert  und einem Endwert
und einem Endwert
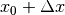 angeben zu können, kann man die Funktionswerte
angeben zu können, kann man die Funktionswerte
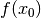 und
und  an den Bereichsgrenzen mit einer
Geraden verbinden und ein entsprechendes Steigungsdreieck einzeichnen. Die
Steigung dieser – üblicherweise als „Sekante“ – bezeichneten Geraden ist nach
Gleichung (1) durch den „Differenzenquotient“
an den Bereichsgrenzen mit einer
Geraden verbinden und ein entsprechendes Steigungsdreieck einzeichnen. Die
Steigung dieser – üblicherweise als „Sekante“ – bezeichneten Geraden ist nach
Gleichung (1) durch den „Differenzenquotient“ 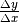 einfach zu berechnen und entspricht der mittleren Steigung der
Funktion
einfach zu berechnen und entspricht der mittleren Steigung der
Funktion 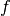 im betrachteten Bereich.
im betrachteten Bereich.
(2)¶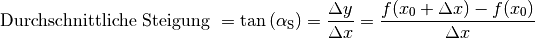
Dabei bezeichnet 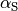 den Winkel, den die
Sekante mit der Horizontalen einschließt.
den Winkel, den die
Sekante mit der Horizontalen einschließt.
Der Wert der Steigung einer Funktion 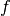 an einer einzigen Stelle
an einer einzigen Stelle 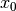 lässt sich mit zunehmender Genauigkeit ermitteln, wenn der Bereich um
die Stelle
lässt sich mit zunehmender Genauigkeit ermitteln, wenn der Bereich um
die Stelle  immer kleiner („feinmaschiger“) gewählt wird. Im
Grenzfall ist
immer kleiner („feinmaschiger“) gewählt wird. Im
Grenzfall ist 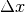 und somit auch das Steigungsdreieck winzig klein.
Die Sekante wird hierbei zu einer Tangente, die den Funktionsgraphen
augenscheinlich nur noch in einem einzigen Punkt berührt. Für die Steigung der
Tangente gilt also:
und somit auch das Steigungsdreieck winzig klein.
Die Sekante wird hierbei zu einer Tangente, die den Funktionsgraphen
augenscheinlich nur noch in einem einzigen Punkt berührt. Für die Steigung der
Tangente gilt also:
(3)¶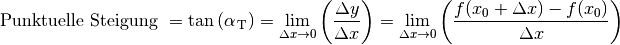
Dabei bezeichnet 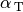 den Winkel, den die
Sekante mit der Horizontalen einschließt.
den Winkel, den die
Sekante mit der Horizontalen einschließt.
Das Schrumpfen des angelegten Steigungsdreiecks um einen bestimmten Punkt herum
ähnelt gewissermaßen dem Zusammenziehen eines Knotens. In der mathematischen
Symbolik wird bei „infinitesimal“ kleinen Steigungsdreiecken anstelle des
griechischen Großbuchstabens  der Kleinbuchstabe
der Kleinbuchstabe
 geschrieben. Der Differenzenquotient
geschrieben. Der Differenzenquotient 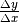 wird dabei zum so genannten Differentialquotienten
wird dabei zum so genannten Differentialquotienten
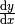 :
:
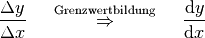
Differenzierbarkeit an einer Stelle  ¶
¶
Die Steigung einer Funktion 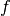 an einer Stelle
an einer Stelle  ist
nur dann eindeutig festgelegt, wenn die Steigungen in der unmittelbaren
Umgebung links und rechts der Stelle gleich sind. Dies ist fast immer der Fall,
doch es gibt Ausnahmen.
ist
nur dann eindeutig festgelegt, wenn die Steigungen in der unmittelbaren
Umgebung links und rechts der Stelle gleich sind. Dies ist fast immer der Fall,
doch es gibt Ausnahmen.
Beispiel:
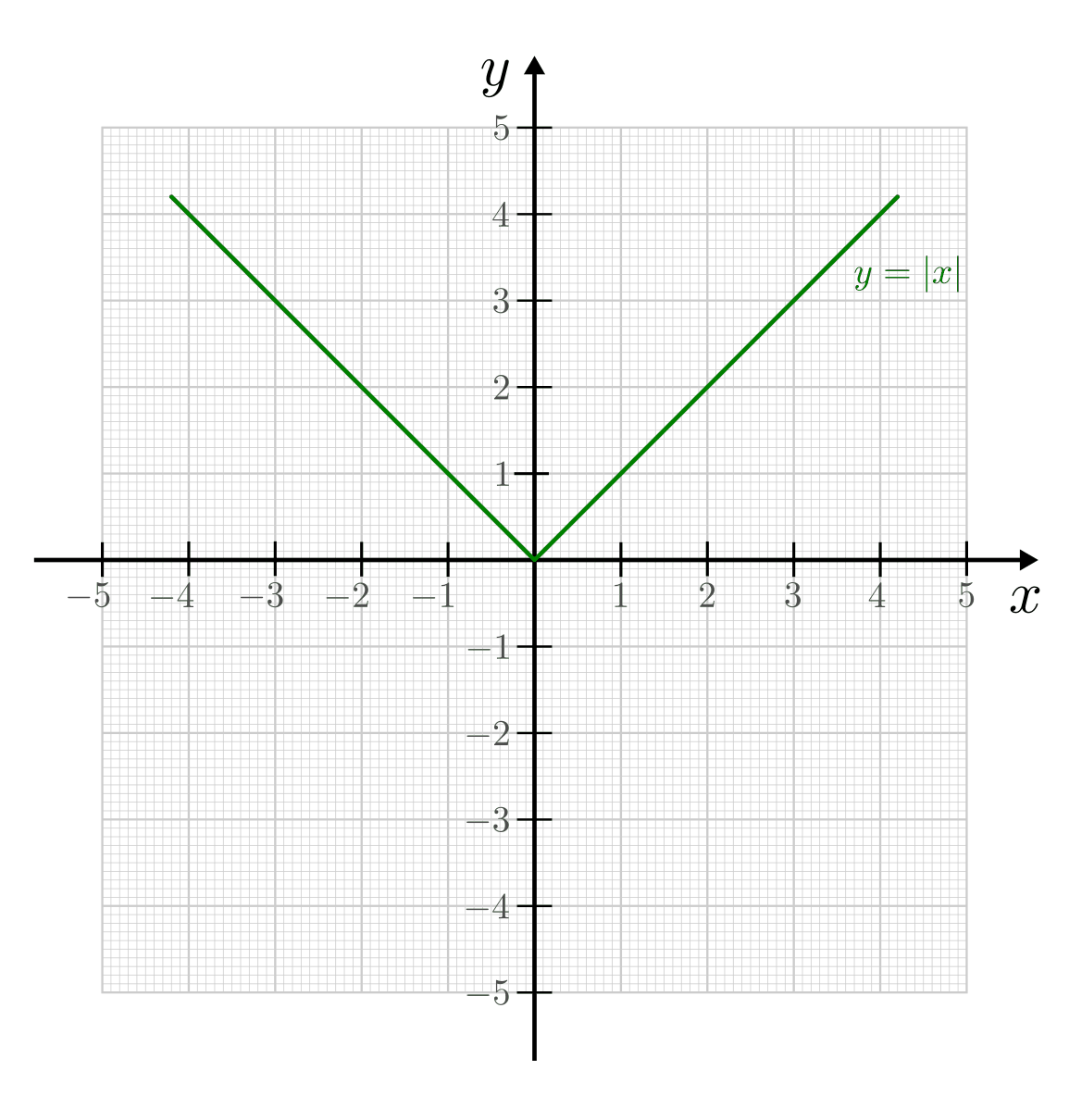
- Der Graph der Betragsfunktion
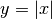 besitzt einen Knick an der
Stelle
besitzt einen Knick an der
Stelle 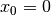 . Zeichnet man ein Steigungsdreieck links und
rechts dieser Stelle ein, so besitzt die Steigungsgerade auf der linken Seite
die Steigung
. Zeichnet man ein Steigungsdreieck links und
rechts dieser Stelle ein, so besitzt die Steigungsgerade auf der linken Seite
die Steigung 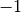 , auf der rechten Seite hingegen den Wert
, auf der rechten Seite hingegen den Wert 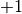 .
An der Stelle
.
An der Stelle 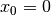 ist die Steigung nicht festgelegt – die
Funktion ist an dieser Stelle nicht differenzierbar.
ist die Steigung nicht festgelegt – die
Funktion ist an dieser Stelle nicht differenzierbar.
Anschaulich sind Funktionen dann differenzierbar, wenn sich die Steigung ihrer Graphen kontinuierlich ändert, die Graphen also keinen „Knick“ besitzen. Hierauf ist insbesondere an den Bereichsgrenzen von abschnittsweise definierten Funktionen (z.B. Signumsfunktion, Betragsfunktion, Stufenfunktion, usw.) sowie an Polstellen von gebrochen-rationalen Funktionen zu achten.
Besitzt eine Funktion eine Definitionslücke, so kann an dieser Stelle nichts über die Differenzierbarkeit der Funktion ausgesagt werden.
Um die Steigung unmittelbar links und unmittelbar rechts der Stelle  berechnen zu können, wählt man die Stelle
berechnen zu können, wählt man die Stelle  selbst als Bereichsgrenze.
Wählt man als zweite Bereichsgrenze
selbst als Bereichsgrenze.
Wählt man als zweite Bereichsgrenze  -Werte, die nur ein wenig kleiner
bzw. größer als
-Werte, die nur ein wenig kleiner
bzw. größer als  sind, so erhält man Steigungsdreiecke, die
unmittelbar links bzw. rechts der untersuchten Stelle an der Funktion anliegen.
sind, so erhält man Steigungsdreiecke, die
unmittelbar links bzw. rechts der untersuchten Stelle an der Funktion anliegen.
Mathematisch lassen sich die beiden unmittelbar angrenzenden Steigungen wie folgt ausdrücken:
![\text{ Steigung links von $x_0$: } = \lim _{\substack{\Delta x \to 0,\\[3pt] \Delta x < 0\;} }
\left( \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\right) \\[12pt]
\text{ Steigung rechts von $x_0$: } = \lim _{\substack{\Delta x \to 0,\\[3pt] \Delta x > 0 \;} }
\left( \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\right)](../../_images/math/63f3c0eb8c217607e10d08d0c18b2fa7e75f116e.png)
Stimmen die beiden Grenzwerte auf linken und auf der rechten Seite der Stelle
 überein, so ist die Funktion an dieser Stelle
differenzierbar, und der Wert ihre Steigung ist gleich dem Steigungswert der
beiden Grenzwerte.
überein, so ist die Funktion an dieser Stelle
differenzierbar, und der Wert ihre Steigung ist gleich dem Steigungswert der
beiden Grenzwerte.
Beispiel:
Die Funktion
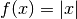 soll auf Differenzierbarkeit an der Stelle
soll auf Differenzierbarkeit an der Stelle
 hin untersucht werden.
hin untersucht werden.Um die Betragstriche weglassen zu können, zerlegt man die Funktion in zwei Teilfunktionen
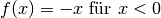 und
und 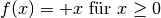 . An der Stelle
. An der Stelle 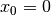 gilt somit für den
linksseitigen Grenzwert:
gilt somit für den
linksseitigen Grenzwert:![\lim _{\substack{\Delta x \to 0,\\[3pt] \Delta x < 0\;} } \left(
\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\right) &= \lim
_{\substack{\Delta x \to 0,\\[3pt] \Delta x < 0\;} } \left( \frac{|x_0 +
\Delta x| - |x_0|}{\Delta x}\right) = \lim _{\substack{\Delta x \to
0,\\[3pt] \Delta x < 0\;} } \left(\frac{-\Delta x}{\Delta x}\right) =
-1 \\[6pt]
\lim _{\substack{\Delta x \to 0,\\[3pt] \Delta x > 0\;} } \left(
\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\right) &= \lim
_{\substack{\Delta x \to 0,\\[3pt] \Delta x > 0\;} } \left( \frac{|x_0 +
\Delta x| - |x_0|}{\Delta x}\right) = \lim _{\substack{\Delta x \to
0,\\[3pt] \Delta x > 0\;} } \left( \frac{+\Delta x}{\Delta x}\right) =
+1 \\[6pt]](../../_images/math/1f2f7f5e9478196488c61fca8b1252ac13fd4b4c.png)
Hierbei wurde jeweils
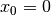 eingesetzt und die Betragsfunktion in
Abhängigkeit des Vorzeichens von
eingesetzt und die Betragsfunktion in
Abhängigkeit des Vorzeichens von 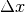 ausgewertet. Der
linksseitige und der rechtsseitige Grenzwert stimmen nicht überein, die
Funktion ist somit an der Stelle
ausgewertet. Der
linksseitige und der rechtsseitige Grenzwert stimmen nicht überein, die
Funktion ist somit an der Stelle 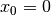 nicht differenzierbar.
nicht differenzierbar.An jeder anderen Stelle, beispielsweise
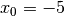 , ist die Funktion
, ist die Funktion
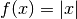 jedoch differenzierbar, denn dabei gilt:
jedoch differenzierbar, denn dabei gilt:![\lim _{\substack{\Delta x \to 0,\\[3pt] \Delta x < 0\;} } \left(
\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\right) &= \lim
_{\substack{\Delta x \to 0,\\[3pt] \Delta x < 0\;} } \left(\frac{|x_0 +
\Delta x| - |x_0|}{\Delta x}\right) \\[4pt] = \lim _{\substack{\Delta x
\to 0,\\[3pt] \Delta x < 0\;} } \left( \frac{|-5 + \Delta x| -
|-5|}{\Delta x}\right) &= \lim _{\substack{\Delta x \to 0,\\[3pt] \Delta
x < 0\;} } \left(\frac{+5 - \Delta x - 5}{\Delta x}\right) = -1 \\[6pt]](../../_images/math/dee00309e234717818e7ba8430f6c87aca262268.png)
Dieser Wert des Differentialquotienten gilt in diesem Fall sowohl für positive wie für negative
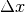 -Werte, da diese im Vergleich zu
-Werte, da diese im Vergleich zu  klein sind und daher keine Auswirkung auf das Vorzeichen der Betragsfunktion
haben.
klein sind und daher keine Auswirkung auf das Vorzeichen der Betragsfunktion
haben.
Herleitung von Ableitungsregeln¶
Um die Steigung einer Funktion  für beliebige Punkte angeben zu
können, ist es nützlich, eine Funktion
für beliebige Punkte angeben zu
können, ist es nützlich, eine Funktion 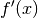 zu finden, deren
Funktionswerte eben den Werten der Steigungen von
zu finden, deren
Funktionswerte eben den Werten der Steigungen von  entsprechen. Die
Funktion
entsprechen. Die
Funktion 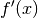 wird dabei als „Ableitung“ von
wird dabei als „Ableitung“ von  , die
Bestimmung von
, die
Bestimmung von  als „Ableiten“ von
als „Ableiten“ von  bezeichnet.
bezeichnet.
Um eine allgemeine Ableitungsregel für beliebige  -Werte herzuleiten,
wird zunächst der Differentialquotient für die betrachtete Funktion aufgestellt.
Durch geschickte Umformungen versucht man anschließend, den zu untersuchenden
Term auf bekannte Grenzwerte hin zurückzuführen (beispielsweise gegen Null
konvergierende Terme). Als Ergebnis erhält man dann einen Ausdruck, der die
Ableitung
-Werte herzuleiten,
wird zunächst der Differentialquotient für die betrachtete Funktion aufgestellt.
Durch geschickte Umformungen versucht man anschließend, den zu untersuchenden
Term auf bekannte Grenzwerte hin zurückzuführen (beispielsweise gegen Null
konvergierende Terme). Als Ergebnis erhält man dann einen Ausdruck, der die
Ableitung 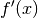 der Funktion angibt.
der Funktion angibt.
Beispiele:
Die Ableitung für die Funktion
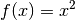 soll anhand des
Differentialquotienten bestimmt werden.
soll anhand des
Differentialquotienten bestimmt werden.Der Differentialquotient für diese Funktion lautet allgemein:
![&\phantom{=\;} \lim _{\Delta x \to 0} \left( \frac{f(x + \Delta x) -
f(x)}{\Delta x}\right) = \lim _{\Delta x \to 0} \left( \frac{(x + \Delta
x)^2 - x^2}{\Delta x}\right) \\[6pt]
&= \lim _{\Delta x \to 0} \left( \frac{x^2 + 2 \cdot x \cdot \Delta x +
(\Delta x)^2 - x^2}{\Delta x} \right) = \lim _{\Delta x \to 0} \left(2
\cdot x + \Delta x \right) = 2 \cdot x](../../_images/math/31f3a2510a04718f8c948095ac135769c8605944.png)
In der zweiten Zeile wurde hierbei zunächst die binomische Formel ausmultipliziert, wobei sich die
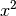 -Terme wegen des unterschiedlichen
Vorzeichens aufheben. Anschließend wurde im Zähler
-Terme wegen des unterschiedlichen
Vorzeichens aufheben. Anschließend wurde im Zähler 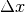 ausgeklammert und gekürzt.
ausgeklammert und gekürzt.Für die Funktion
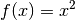 ist die zugehörige Ableitungsfunktion
somit
ist die zugehörige Ableitungsfunktion
somit 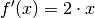 .
.Die Ableitung für die Funktion
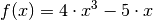 soll
anhand des Differentialquotienten bestimmt werden.
soll
anhand des Differentialquotienten bestimmt werden.Der Differentialquotient für diese Funktion lautet allgemein:
![&\phantom{=\;} \lim _{\Delta x \to 0} \left( \frac{f(x + \Delta x) -
f(x)}{\Delta x}\right) = \lim _{\Delta x \to 0} \left( \frac{\big(4 \cdot
(x + \Delta x)^3 - 5 \cdot (x+ \Delta x)\big) - \big(4 \cdot x^3 - 5
\cdot x\big)}{\Delta x}\right) \\[6pt]
&= \lim _{\Delta x \to 0} \left( \frac{\big(4 \cdot (x^3 +
3\!\cdot\!x^2\!\cdot\!\Delta x + 3\!\cdot\!x\!\cdot \!(\Delta x)^2 +
(\Delta x)^3 - 5\!\cdot\!x - 5\!\cdot\!\Delta x \big) - (4 \cdot x^3
-5 \cdot x)}{\Delta x} \right) \\[6pt]
&=\lim _{\Delta x \to 0} \left( \frac{12\!\cdot\!x^2\!\cdot\!\Delta x
+12\!\cdot\!x\!\cdot\!(\Delta x)^2- 5 \cdot \Delta x}{\Delta x}\right)
=\lim _{\Delta x \to 0} \left( 12 \cdot x^2 + 12 \cdot x \cdot
\Delta x - 5 \right) = 12 \cdot x^2 - 5](../../_images/math/290ede8f9d93bd2cc643ce533d5786bb1f26db29.png)
In der zweiten Zeile wurde hierbei wiederum die binomische Formel ausmultipliziert, wobei sich die
 -Terme und
-Terme und
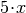 -Terme jeweils wegen der unterschiedlichen Vorzeichen
aufheben. Anschließend wurde im Zähler
-Terme jeweils wegen der unterschiedlichen Vorzeichen
aufheben. Anschließend wurde im Zähler 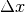 ausgeklammert und
gekürzt; im resultierenden Ausdruck geht der Term
ausgeklammert und
gekürzt; im resultierenden Ausdruck geht der Term 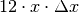 wegen
wegen 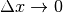 gegen Null.
gegen Null.Für die Funktion
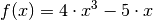 ist die zugehörige
Ableitungsfunktion somit
ist die zugehörige
Ableitungsfunktion somit 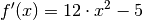 .
.
Glücklicherweise wurden, wie in den nächsten Abschnitten näher beschrieben ist, mit Hilfe der obigen Methode für alle elementaren Funktionen allgemeine Ableitungsregeln hergeleitet, so dass man die Ableitung einer Funktion in praktischen Anwendungen sehr häufig mit deutlich weniger Rechenaufwand bestimmen kann.



 . An der Stelle
. An der Stelle