Grundrechenarten und Rechenregeln¶
Ziffern und Zahlen im Dezimalsystem¶
Im so genannten „Dezimalsystem“ werden Zahlen durch die Ziffern 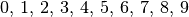 repräsentiert. Um beliebig
große Zahlen mit nur diesen zehn Ziffern darstellen zu können, besitzt jede
Ziffer neben ihrem eigentlichen Wert auch einen bestimmten Stellenwert. Der
tatsächliche Wert einer Ziffer entspricht damit ihrem Eigenwert multipliziert
mit ihrem Stellenwert.
repräsentiert. Um beliebig
große Zahlen mit nur diesen zehn Ziffern darstellen zu können, besitzt jede
Ziffer neben ihrem eigentlichen Wert auch einen bestimmten Stellenwert. Der
tatsächliche Wert einer Ziffer entspricht damit ihrem Eigenwert multipliziert
mit ihrem Stellenwert.
Die Zahlen 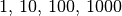 beziehungsweise
beziehungsweise 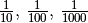 usw. werden als Stufenzahlen oder
Zehnerpotenzen bezeichnet. Mit ihrer Hilfe lässt sich jede Zahl eindeutig
als Summe von Vielfachen der Stufenzahlen schreiben.
usw. werden als Stufenzahlen oder
Zehnerpotenzen bezeichnet. Mit ihrer Hilfe lässt sich jede Zahl eindeutig
als Summe von Vielfachen der Stufenzahlen schreiben.
In der Dezimal-Schreibweise wird bei der Darstellung großer Zahlen nach den
Ziffern für 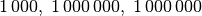 usw. nach
Möglichkeit je ein kleiner Zwischenraum eingefügt, um die Lesbarkeit zu erhöhen.
Ziffern mit einer Wertigkeit kleiner als Eins werden im deutschen Sprachraum mit
einem Komma, im Englischen mit einem Punkt von den übrigen getrennt.
usw. nach
Möglichkeit je ein kleiner Zwischenraum eingefügt, um die Lesbarkeit zu erhöhen.
Ziffern mit einer Wertigkeit kleiner als Eins werden im deutschen Sprachraum mit
einem Komma, im Englischen mit einem Punkt von den übrigen getrennt.
Die vier Grundrechenarten¶
Mathematik ist die Wissenschaft der Zahlen. Die mathematischen Operationen Addition, Subtraktion, Multiplikation und Division stellen im alltäglichen Leben die wohl gebräuchlichsten Verknüpfungen von Zahlen dar; sie werden daher auch als Grundrechenarten bezeichnet.
Die Addition
Werden zwei Zahlen oder Terme mit einem Pluszeichen verbunden, so bezeichnet man den Rechenausdruck als Summe. Die einzelnen Zahlen, die addiert werden, heißen Summanden.
Ohne Computer oder Taschenrechner lassen sich Zahlen am einfachsten addieren, indem sie untereinander geschrieben werden. Dabei müssen die Ziffern mit gleicher Wertigkeit (Einer, Zehner Hunderter usw.) immer genau untereinander stehen. Anschließend werden spaltenweise von rechts nach links die Ziffern der einzelnen Summanden addiert. Treten dabei Werte größer als Zehn auf, so wird nur die Einerstelle der jeweiligen Summe unter den Strich geschrieben, die Zehnerstelle wird als „Übertrag“ in die nächste Ziffernstelle übernommen.[1]
Der Grundgedanke hierbei besteht darin, dass jeweils zehn „Einer“ mit einem „Zehner“, zehn „Zehner“ mit einem „Hunderter“ usw. gleichwertig sind. Bei der Addition der einzelnen Stellenwerte kann man somit jeweils zehn Repräsentanten einer Wertigkeit durch einen Repräsentanten der nächst höheren Wertigkeit ersetzen und diesen zur Addition des nächsten Stellenwertes hinzunehmen.
Die Subtraktion
Werden zwei Zahlen oder Terme mit einem Minuszeichen verbunden, so bezeichnet man den Rechenausdruck als Differenz. Vor dem Minuszeichen steht der Minuend, dahinter der Subtrahend.
Auch bei der schriftlichen Subtraktion werden die Ziffern mit gleicher Wertigkeit jeweils untereinander geschrieben. Anschließend werden spaltenweise von rechts nach links die Ziffern des Subtrahenden von der jeweiligen Ziffer des Minuenden subtrahiert. Ist dabei die Ziffer des Minuenden kleiner als die des Subtrahenden, so wird die Ziffer des Minuenden um 10 erhöht und der so gebildete Differenzwert unter den Strich geschrieben. Der „Übertrag“ lässt sich dadurch ausgleichen, indem die nächste, um das 10-fache größere Ziffer des Minuenden um Eins erniedrigt wird.[2]
Der Grundgedanke hierbei besteht wiederum darin, dass jeweils ein „Zehner“ mit zehn „Einern“, ein „Hunderter“ mit zehn „Zehnern“ usw. gleichwertig ist. Bei der Subtraktion der einzelnen Stellenwerte kann man somit im Minuenden jeweils einen Repräsentanten einer Wertigkeit durch zehn Repräsentanten der nächst niedrigeren Wertigkeit ersetzen.
Die Multiplikation
Werden zwei Zahlen oder Terme mit einem Malzeichen verbunden, so bezeichnet man den Rechenausdruck als Produkt. Die einzelnen Zahlen beziehungsweise Terme, die miteinander multipliziert werden, heißen Faktoren.
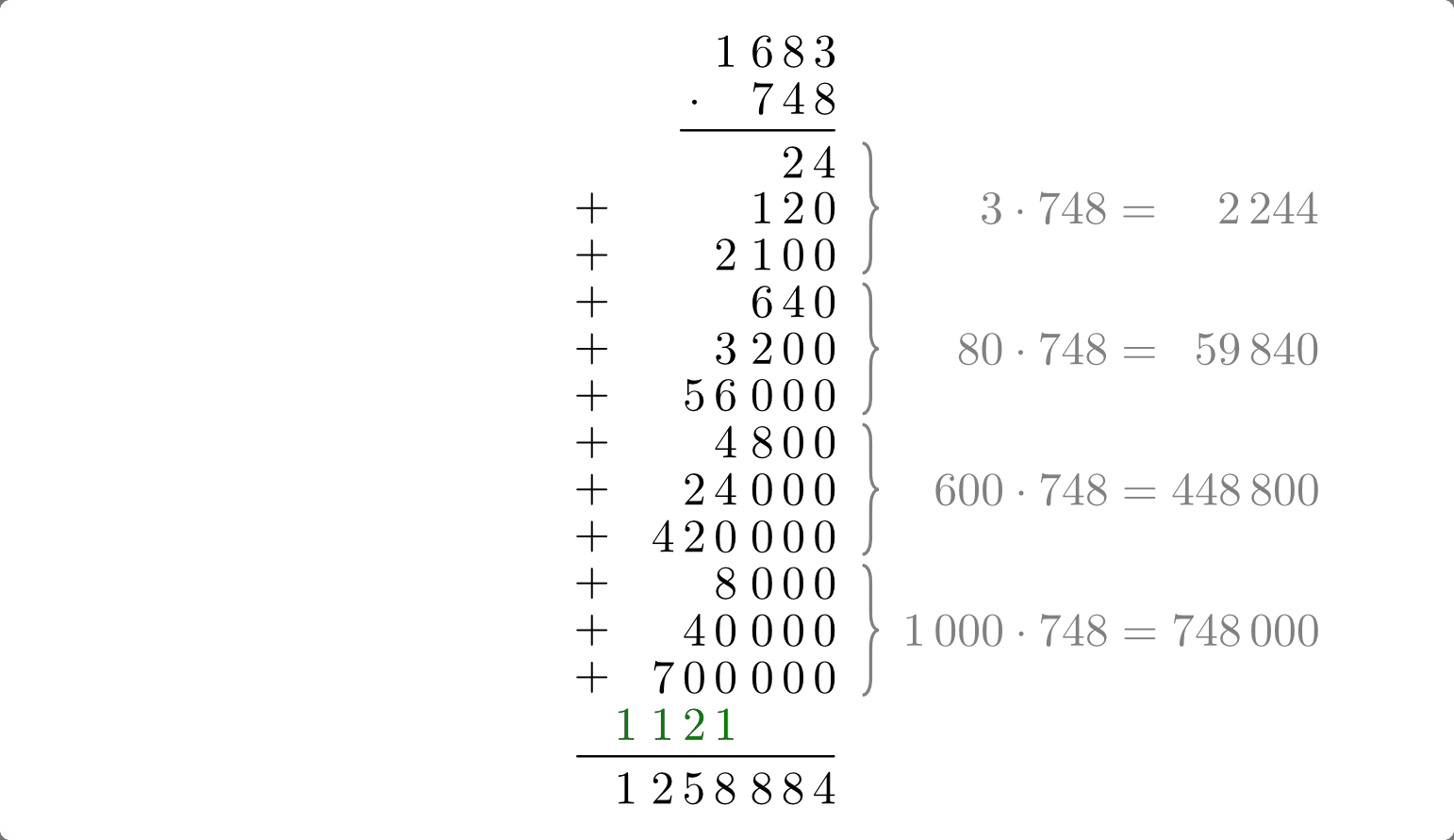
Bei einer schriftlichen Multiplikation wird der erste Faktor spaltenweise von rechts mit allen Ziffern des zweiten Faktors multipliziert. An jedes so gebildete Teilergebnis wird dabei eine Anzahl an Nullen angehängt, die der Summe an Nullen beider Ziffernwertigkeiten entspricht. Die einzelnen Teilergebnisse werden gemäß ihrer Wertigkeiten untereinander geschrieben und aufaddiert.
Der Grundgedanke dieser Rechenmethode liegt darin, dass es sich bei jeder Multiplikation um eine mehrfache Addition handelt. In gleicher Weise, wie man sich eine einzelne Zahl anhand ihrer Ziffern aus den jeweiligen Vielfachen der Stufenzahlen aufgebaut denken kann, kann man sich auch jedes Produkt zweier Zahlen als Summe einzelner Teilfaktoren vorstellen.
Die Division
Werden zwei Zahlen oder Terme mit einem Geteilt-Zeichen verbunden, so bezeichnet man den Rechenausdruck als Division. Vor dem Geteilt-Zeichen steht der Dividend, dahinter der Divisor. Für das Geteilt-Zeichen gibt es mehrere gleichwertige Schreibweisen:
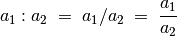
Bei einer schriftlichen Division werden der Dividend, der Divisor und das zu
berechnende Ergebnis in eine Zeile geschrieben. Zunächst werden nur (von links
nach rechts) die ersten  Ziffern des Dividenden betrachtet, so dass
die sich aus den
Ziffern des Dividenden betrachtet, so dass
die sich aus den  Ziffern ergebende Zahl größer ist als der Divisor.
Durch Abschätzen wird ermittelt, welchem ganzzahligen Vielfachen des Divisors
– abgesehen von einem später noch zu bestimmenden Rest – die ausgewählte,
Ziffern ergebende Zahl größer ist als der Divisor.
Durch Abschätzen wird ermittelt, welchem ganzzahligen Vielfachen des Divisors
– abgesehen von einem später noch zu bestimmenden Rest – die ausgewählte,
 -stellige Zahl entspricht. Mit diesem Vielfachen, das die erste
Ergebnis-Ziffer darstellt, wird der Divisor anschließend multipliziert und das
erhaltene Ergebnis von der
-stellige Zahl entspricht. Mit diesem Vielfachen, das die erste
Ergebnis-Ziffer darstellt, wird der Divisor anschließend multipliziert und das
erhaltene Ergebnis von der  -stelligen Zahl subtrahiert. Übrig bleibt
hierbei ein bestimmter Teilungsrest. Zu diesem Rest können nach dem gleichen
Schema weitere Ziffern des Dividenden hinzugenommen und die Division nach der
gleichen Rechenmethode fortgesetzt werden.
-stelligen Zahl subtrahiert. Übrig bleibt
hierbei ein bestimmter Teilungsrest. Zu diesem Rest können nach dem gleichen
Schema weitere Ziffern des Dividenden hinzugenommen und die Division nach der
gleichen Rechenmethode fortgesetzt werden.
Durch die Verwendung von Taschenrechnern und Computern werden die schriftliche Multiplikation und Division im alltäglichen Leben kaum noch angewendet. Das Rechenschema der schriftlichen Division ist allerdings für die Methode der Polynom-Division in der Analysis und Algebra von Bedeutung.
Klammern und Reihenfolge der Auswertung¶
Die vier Grundrechenarten sind als Operatoren für jeweils zwei Operanden festgelegt. Sollen drei oder mehr Zahlen durch die vier Grundrechenarten verknüpft werden, so kann dies nur schrittweise erfolgen.
Die Reihenfolge, in der die einzelnen Operationen ausgeführt werden müssen, ist durch Vorrang-Regeln sowie durch die Verwendung von Klammern festgelegt:
- Was in Klammern steht, wird zuerst ausgewertet (bei Zahlen) beziehungsweise zusammengefasst (bei Variablen).
- Ist durch Klammern keine andere Reihenfolge der Auswertung festgelegt, so werden zunächst die Rechenoperatoren der dritten Stufe (Potenzen und Wurzeln) ausgewertet.
- Als nächstes werden die Rechenoperatoren der zweiten Stufe (Multiplikation und Division) ausgewertet.
- Zuletzt werden die Rechenoperationen der ersten Stufe (Addition und Multiplikation) ausgeführt.
Durch das Setzen von Klammern kann somit eine von der üblichen Regel „(Hoch vor) Punkt vor Strich“ abweichende Reihenfolge der Auswertung erreicht werden. In allgemeiner Form kann die Auswertungsreihenfolge somit als „Klammer vor Hoch vor Punkt vor Strich“ zusammengefasst werden. Die Rechenoperationen gleicher Stufe werden dabei von links nach rechts ausgeführt.
Bei der Verwendung von Klammern sind folgende Regeln zu beachten:
Klammern treten stets paarweise auf („Klammer auf, Klammer zu“)
Mehrere Klammern können ineinander verschachtelt, niemals jedoch überlappend auftreten.
Zur besseren Lesbarkeit werden oftmals verschiedene Klammer-Symbole verwendet:
![\left \langle \ldots \left \lbrace \ldots \left[ \ldots \left(
\phantom{\frac{a}{b} } \ldots \phantom{\frac{a}{b} } \right) \ldots
\right] \ldots \right \rbrace \ldots \right \rangle](../_images/math/36fb921a530f78b77c2c316633cd4e034787f0ab.png)
Als Alternative dazu können Klammern unterschiedlicher Größe genutzt werden:
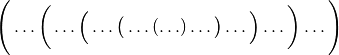
In manchen Fällen kann ein Term durch das Auflösen einer Klammer vereinfacht werden – insbesondere wenn sich verschiedene Terme dadurch leichter zusammenzählen lassen oder sich gegenseitig aufheben (zu Null addieren). Hierzu muss das vor der Klammer stehende Rechenzeichen auf alle Glieder der Klammer angewendet werden. Es gelten damit folgende Regeln:
Steht vor einer Klammer ein Pluszeichen
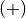 , so kann die Klammer ohne
Änderung der Rechenzeichen innerhalb der Klammer weggelassen werden. Somit
gilt:
, so kann die Klammer ohne
Änderung der Rechenzeichen innerhalb der Klammer weggelassen werden. Somit
gilt:(1)¶
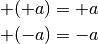
Steht vor einer Klammer ein Minuszeichen
 , so werden alle additiven
Rechenzeichen in der Klammer in die jeweils entgegengesetzten umgewandelt (Plus
wird zu Minus und umgekehrt).
, so werden alle additiven
Rechenzeichen in der Klammer in die jeweils entgegengesetzten umgewandelt (Plus
wird zu Minus und umgekehrt).(2)¶
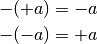
Klammern finden insbesondere dann Anwendung, wenn sowohl additive wie auch multiplikative Terme miteinander kombiniert werden. Die dafür wesentlichen Rechenregeln sind im nächsten Abschnitt zusammengefasst.
Rechengesetze für die Grundrechenarten¶
Häufig muss man bei mathematischen Aufgaben Terme aus Zahlen und/oder Variablen auswerten, welche durch die vier Grundrechenarten verknüpft sind. Zur Vereinfachung können dabei bestimmte Umformungen vorgenommen werden, die für beliebige Variablenwerte aus dem Definitionsbereich stets unveränderte Ergebniswerte liefern. Die drei wichtigsten dieser Rechenregeln werden als Kommutativ-, Assoziativ- und Distributivgesetz bezeichnet.
Das Kommutativgesetz
Bei der Addition und der Multiplikation können die einzelnen Summanden beziehungsweise Faktoren miteinander vertauscht werden. Es gelten somit folgende Rechenregeln:
(3)¶![a_1 + a_2 &= a_2 + a_1 \\[6pt]
a_1 \; \cdot \, a_2 &= a_2 \; \cdot \, a_1](../_images/math/da66d1b9d21d7dae1fb0299e67243753e262ee90.png)
Die Subtraktion und die Division sind nicht kommutativ.
Das Assoziativgesetz
Bei der Addition von mehr als zwei Summanden oder einer Multiplikation mehrerer Faktoren können die Summen- beziehungsweise Produktglieder beliebig durch Klammern gruppiert werden. Es gilt somit:
(4)¶![a_1 + (a_2 + a_3) &= (a_1 + a_2) + a_3 = a_1 + a_2 + a_3 \\[6pt]
a_1 \; \cdot \, (a_2 \; \cdot \; a_3) &= (a _1 \; \cdot \; a_2) \, \cdot
\; a_3 = a_1 \; \cdot \; a_2 \; \cdot \; a_3](../_images/math/f4c15f713911e7039d5d64cf3ab6f6a294ddc74e.png)
Das Assoziativgesetz gilt in entsprechender Form auch für die Subtraktion und die Division.[3]
Das Distributivgesetz
Treten Addition und Multiplikation gemeinsam auf, so gelten folgende Verknüpfungsregeln:
(5)¶![a_1 \cdot (a_2 + a_3 ) = a_1 \cdot a _2 + a_1 \cdot a_3 \\[6pt]
(a_2 + a_3 ) \cdot a_1 = a_2 \cdot a _1 + a_3 \cdot a_1](../_images/math/32dc0ab91e6da3abce34cc836194e29dce5322af.png)
Ist ein Summenterm mit einem Faktor zu multiplizieren, so kann man jeden Summanden einzeln mit dem Faktor multiplizieren und anschließend beide Produkte addieren. Die Reihenfolge der Faktoren beziehungsweise Summanden spielt dabei gemäß dem Kommutativgesetz (3) keine Rolle.
Besitzen im umgekehrten Fall alle Summanden einer Summe einen gemeinsamen Faktor, so kann dieser gemäß der obigen Gleichung „ausgeklammert“ werden. Dieser Rechentrick, auch als „Faktorisierung“ einer Summe bezeichnet, wird insbesondere bei der Rechnung mit Brüchen häufig angewendet.
Das Distributivgesetz gilt in entsprechender Form auch für die Subtraktion und die Division.[4]
Binomische Formeln¶
Sollen zwei in Klammern stehende Summenterme miteinander multipliziert werden, so kann ebenfalls das Distributivgesetz angewendet werden. Jeder Summand des ersten Terms ist dabei mit jedem Summanden des zweiten Terms (unter Berücksichtigung des Vorzeichens) zu multiplizieren. Beispielsweise gilt:
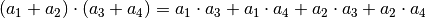
Bestehen die zu multiplizierenden Summenterme wie im obigen Beispiel aus jeweils zwei Summanden, so werden sie als Binome bezeichnet. Für sie gelten folgende, für vielerlei Aufgaben nützliche „binomische Formeln“:
(6)¶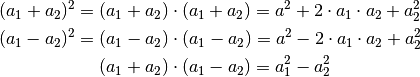
Für höhere Potenzen kann mit Hilfe des Summenzeichens und des so genannten Binomialkoeffizienten eine allgemeine binomische Formel angegeben werden:
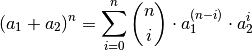
Für 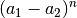 wechseln sich die Vorzeichen der einzelnen Produkte
ab. Dies kann in der obigen Formel durch einen Faktor
wechseln sich die Vorzeichen der einzelnen Produkte
ab. Dies kann in der obigen Formel durch einen Faktor 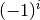 berücksichtigt werden, der je nach Wert der Indexvariablen
berücksichtigt werden, der je nach Wert der Indexvariablen 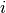 ein
positives oder negatives Vorzeichen liefert. Somit gilt:
ein
positives oder negatives Vorzeichen liefert. Somit gilt:
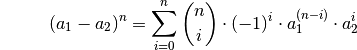
Beträge und Einheiten¶
Der Betrag 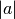 einer Zahl ist die nicht-negative der beiden Zahlen
einer Zahl ist die nicht-negative der beiden Zahlen
 und
und 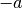 :
:
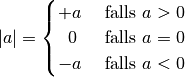
Anschaulich entspricht der Betrag 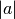 einer Zahl
einer Zahl  dem
Abstand zwischen
dem
Abstand zwischen  und
und  auf der Zahlengeraden.
auf der Zahlengeraden.
Rechnen mit Beträgen
Da Beträge letztlich nichts anderes sind als positive reelle Zahlen, können sie beliebig mit den vier Grundrechenarten verknüpft werden. Für die Beträge von Produkten und Quotienten gelten dabei folgende Rechenregeln:
![| a_1 \cdot a_2 | &= | a_1 | \cdot | a_2 | \\[4pt]
| a_1 : a_2 | &= | a_1 | : | a_2 | \\[4pt]](../_images/math/42df5837379db95f61ffff51faeaf7511f196ed5.png)
Die Gleichung 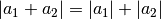 gilt nicht allgemein,
sondern nur dann, wenn
gilt nicht allgemein,
sondern nur dann, wenn 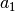 und
und 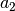 das gleiche Vorzeichen
besitzen; andernfalls ist der Betrag der Summen
das gleiche Vorzeichen
besitzen; andernfalls ist der Betrag der Summen 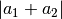 kleiner als
die Summe der Beträge
kleiner als
die Summe der Beträge 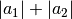 . Beide Fälle lassen sich durch
folgende Ungleichung beschreiben:
. Beide Fälle lassen sich durch
folgende Ungleichung beschreiben:
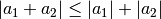
Häufig ist auch der Differenzbetrag zweier Zahlen 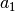 und
und 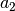 von Interesse, d.h. der Abstand
von Interesse, d.h. der Abstand 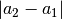 zwischen
zwischen 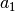 und
und
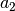 auf der Zahlengeraden. Der Differenzbetrag entspricht somit der
Differenz beider Zahlen ohne Berücksichtigung des Vorzeichens. Hierbei gilt:
auf der Zahlengeraden. Der Differenzbetrag entspricht somit der
Differenz beider Zahlen ohne Berücksichtigung des Vorzeichens. Hierbei gilt:
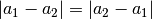
Rechnen mit Einheiten
In anwendungsorientierten Aufgaben muss meist nicht nur mit Zahlen, sondern auch mit (physikalischen) Größen gerechnet werden. Diese haben in den meisten Fällen nicht nur einen bestimmten Betrag beziehungsweise Zahlenwert, sondern auch eine bestimmte Einheit.
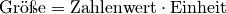
Wird in einer Gleichung mit Größen gerechnet, so müssen sich die jeweiligen Einheiten auf beiden Seiten der Gleichung stets entsprechen. Dabei sind folgende Regeln zu beachten:
Identische Größen haben im allgemeinen Sprachgebrauch teilweise unterschiedliche Bezeichnungen. Auch hierbei sind die jeweiligen Umrechnungsfaktoren zu berücksichtigen.
Beispiele:
![\unit[1]{Liter} = \unit[1]{Kubikdezimeter} \\[8pt]
\unit[1]{Tonne} = \unit[1\,000]{Kilogramm}](../_images/math/085c335c06482d141ef40927576366244b03c4db.png)
Durch Verwendung von Zehnerpotenzen beziehungsweise den entsprechenden „Vorsätzen“ (Kilo-, Mega-, Giga- beziehungsweise Zenti-, Mili-, Mikro- usw.) lassen sich Einheiten oftmals „einfacher“ darstellen. Dabei müssen die Zahlenwerte der Einheiten entsprechend angepasst werden.
Beispiele:
![\unit[1]{m} = \unit[100]{cm} = \unit[1\,000]{mm} \\[8pt]
\unit[1]{MW} = \unit[1\,000]{kW} = \unit[1\,000\,000]{W}](../_images/math/ca8d4f0d9ca1d80c2619e1f190bc4e4d680f6657.png)
Anmerkungen:
| [1] | Der Übertrag kann wahlweise über den ersten Summanden oder direkt über den Bruchstrich geschrieben werden. Letztere Schreibweise wird bevorzugt, wenn auf diese Weise mehr als zwei Zahlen addiert werden. |
| [2] | Alternativ zur Erniedrigung der nächst größeren Ziffer des Minuenden kann der Übertrag auch dadurch berücksichtigt werden, dass die nächst größere Ziffer des Subtrahenden um Eins erhöht wird. Sollen mehrere Zahlen auf einmal vom Minuenden subtrahiert werden, so kann man die einzelnen Subtrahenden – Ziffer für Ziffer – zunächst aufaddieren, um sie dann als Summe vom Minuenden abzuziehen. |
| [3] | Für das Assoziativgesetz bzgl. der Addition und Subtraktion gilt:
Für Multiplikations- und Divisionsklammern, d.h. Klammern in denen nur Mal- und Geteiltzeichen, aber keine Additions- und Subtraktionszeichen als Rechenoperatoren vorkommen, gilt das Assoziativgesetz in folgender Form:
In jedem Fall muss darauf geachtet werden, dass nicht durch Null dividiert
wird. Bei den letzten drei Gleichungen muss daher die Bedingung |
| [4] | Für die Kombination der Subtraktion und Multiplikation gilt das Distributivgesetz in folgender Form:
Für die Kombination der Addition oder Subtraktion mit der Division gilt
(jeweils mit
|


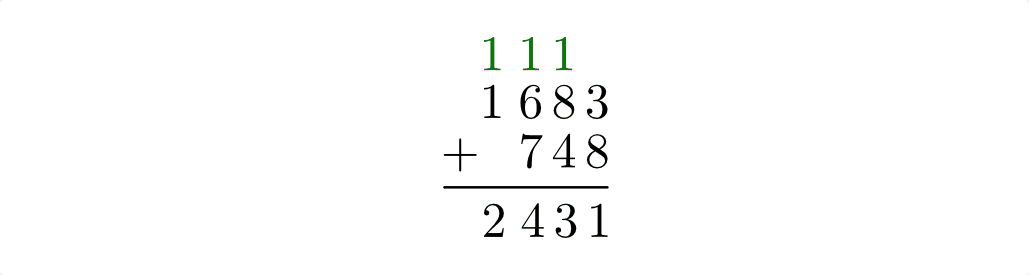
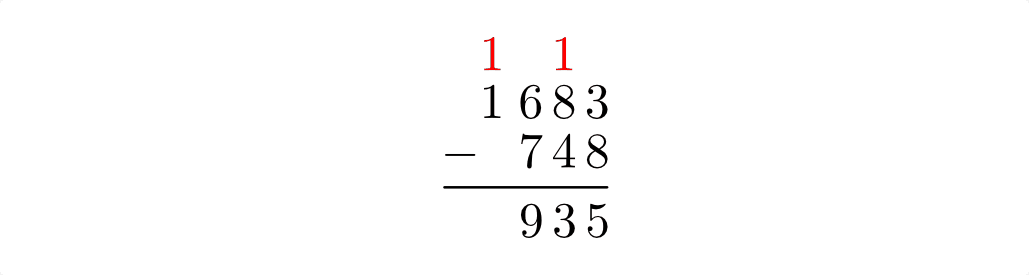
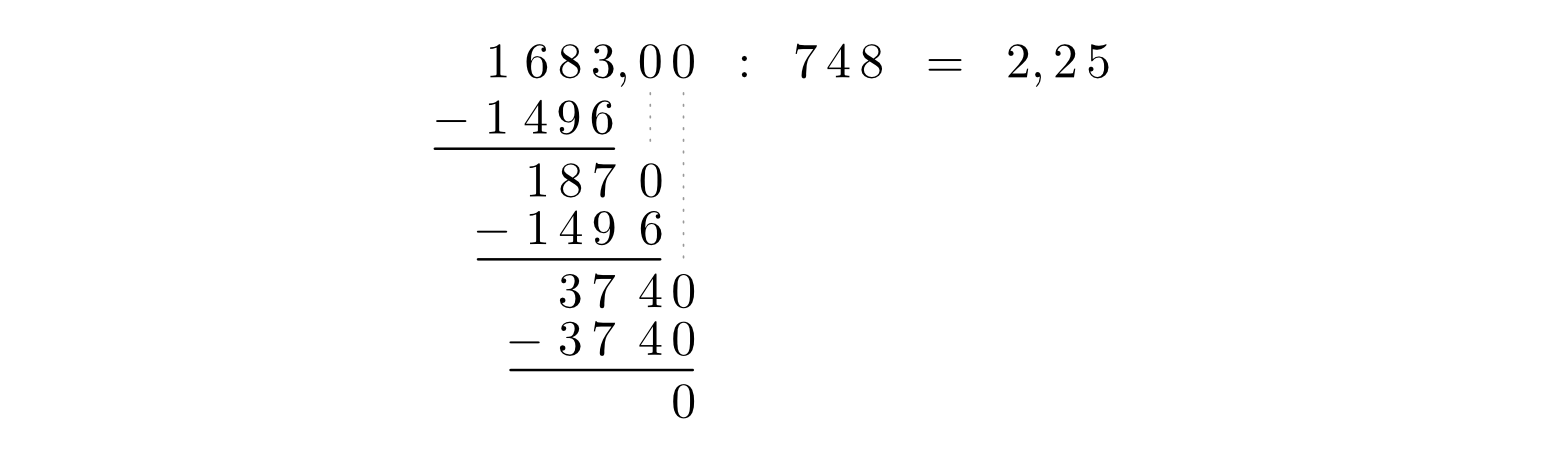
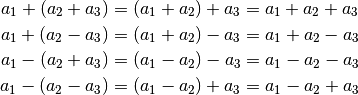
 , so kann die Klammer ohne Änderung der
Rechenzeichen in der Klammer weggelassen werden.
, so kann die Klammer ohne Änderung der
Rechenzeichen in der Klammer weggelassen werden.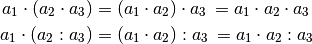
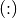 , so kann die Klammer weggelassen werden, wenn
alle Rechenzeichen in die entgegengesetzten umgewandelt werden (hierbei
ist „Mal“ durch „Geteilt“ und „Geteilt“ durch „Mal“ zu ersetzen).
, so kann die Klammer weggelassen werden, wenn
alle Rechenzeichen in die entgegengesetzten umgewandelt werden (hierbei
ist „Mal“ durch „Geteilt“ und „Geteilt“ durch „Mal“ zu ersetzen).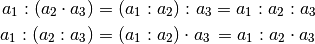
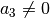 eingehalten werden, in den letzten beiden muss zusätzlich
eingehalten werden, in den letzten beiden muss zusätzlich 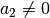 gelten.
gelten.![a_1 \cdot (a_2 - a_3 ) = a_1 \cdot a _2 - a_1 \cdot a_3 \\[4pt]
(a_2 - a_3) \cdot a_1 = a_2 \cdot a _1 - a_3 \cdot a_1](../_images/math/fbb01d69d262a9ef45a51f0d4b44232d7cc95ed9.png)
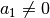 ):
):![(a_2 + a_3 ) : a_1 = a_2 : a_1 + a_3 : a_1 \\[4pt]
(a_2 - a_3 ) : a_1 = a_2 : a_1 - a_3 : a_1](../_images/math/79bc1866cb3a4c9aae470758b2553572f2021eda.png)