Algebraische Gleichungen höheren Grades¶
Bei einer algebraischen Gleichung  -ten Grades tritt die Variable
-ten Grades tritt die Variable
 in der Potenz
in der Potenz 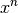 und gegebenenfalls in Potenzen niederen
Grades auf; sie darf dabei nicht im Nenner stehen. Jede algebraische Gleichung
kann durch äquivalente Umformungen in die allgemeine Form gebracht werden:
und gegebenenfalls in Potenzen niederen
Grades auf; sie darf dabei nicht im Nenner stehen. Jede algebraische Gleichung
kann durch äquivalente Umformungen in die allgemeine Form gebracht werden:
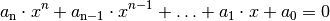
Der Term auf der linken Seite der obigen Gleichung, der aus einer Summe von
Vielfachen von Potenzen einer Variablen (meist  ) besteht, wird
allgemein als „Polynom“ bezeichnet.
) besteht, wird
allgemein als „Polynom“ bezeichnet.
Algebraische Gleichungen lassen sich im Allgemeinen nur näherungsweise mit Hilfe
eines geeigneten Computerprogramms[1] lösen. Eine Gleichung  -ten
Grades hat dabei maximal
-ten
Grades hat dabei maximal  Lösungen. Unmittelbar rechnerisch lösbar sind
Gleichungen dritten oder höheren Grades jedoch dann, wenn einer der
folgenden Sonderfälle vorliegt:
Lösungen. Unmittelbar rechnerisch lösbar sind
Gleichungen dritten oder höheren Grades jedoch dann, wenn einer der
folgenden Sonderfälle vorliegt:
- Fehlt bei einer Gleichung
 -ten Grades das
-ten Grades das  -freie Glied, so
kann auf der linken Gleichungsseite
-freie Glied, so
kann auf der linken Gleichungsseite  ausgeklammert werden. Damit ist
ausgeklammert werden. Damit ist
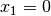 als (erste) Lösung der Gleichung gefunden. Der
verbleibende Term muss als Gleichung
als (erste) Lösung der Gleichung gefunden. Der
verbleibende Term muss als Gleichung 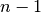 -ten Grades separat gelöst
werden.[2] Beispielsweise lassen sich auf diese Weise Gleichungen dritten
Grades („kubische Gleichungen“) auf quadratische Gleichungen zurückführen, die
mit Hilfe der Mitternachtsformel gelöst werden können.
-ten Grades separat gelöst
werden.[2] Beispielsweise lassen sich auf diese Weise Gleichungen dritten
Grades („kubische Gleichungen“) auf quadratische Gleichungen zurückführen, die
mit Hilfe der Mitternachtsformel gelöst werden können.
Treten bei einer algebraischen Gleichung vierten Grades nur gerade Exponenten auf, d.h. gilt
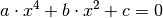 , so kann die
Gleichung durch die Einführung einer neuen Variablen
, so kann die
Gleichung durch die Einführung einer neuen Variablen 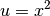 auf eine
quadratische Form gebracht werden. Dieses Verfahren wird als Substitution
bezeichnet. Es gilt:
auf eine
quadratische Form gebracht werden. Dieses Verfahren wird als Substitution
bezeichnet. Es gilt: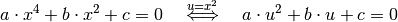
Ist die neue quadratische Gleichung für
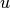 gelöst (mit den Lösungen
gelöst (mit den Lösungen
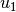 und
und 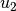 ), so können anhand der Gleichung
), so können anhand der Gleichung
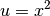 wiederum die Lösungen der ursprünglichen Gleichung berechnet
werden („Rücksubstitution“).[3] Es folgt:
wiederum die Lösungen der ursprünglichen Gleichung berechnet
werden („Rücksubstitution“).[3] Es folgt: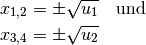
Da Potenzieren und Wurzelziehen nicht unbedingt äquivalente Umformungen einer Gleichung darstellen, muss durch Einsetzen überprüft werden, ob die so gefundenen Werte tatsächlich Lösungen der ursprünglichen Gleichung sind.
Die Substitutions-Methode ist allgemein für Gleichungen der Form
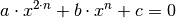 anwendbar, wenn
anwendbar, wenn 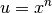 eingesetzt wird.
eingesetzt wird.
Ist eine Lösung
 einer algebraischen Gleichung höheren
Grades bekannt oder kann sie durch Ausprobieren einfach ermittelt werden, so
kann die Gleichung – wie bei einer Linearfaktorzerlegung – in ein Produkt aus
einer algebraischen Gleichung höheren
Grades bekannt oder kann sie durch Ausprobieren einfach ermittelt werden, so
kann die Gleichung – wie bei einer Linearfaktorzerlegung – in ein Produkt aus 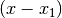 und
einem Restterm zerlegt werden. Dieser Restterm kann in umgekehrter Weise
berechnet werden, indem man den ursprünglichen Term durch
und
einem Restterm zerlegt werden. Dieser Restterm kann in umgekehrter Weise
berechnet werden, indem man den ursprünglichen Term durch 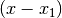 teilt. Es gilt somit:
teilt. Es gilt somit: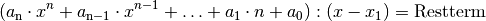
Diese so genannte „Polynomdivision“ wird nach einem ähnlichen Verfahren durchgeführt wie die schriftliche Division:
- Zunächst wird der erste Summand
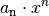 des
ursprünglichen Terms durch
des
ursprünglichen Terms durch  geteilt. Das erste Teilergebnis
geteilt. Das erste Teilergebnis
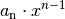 wird auf die rechte Seite des
Istgleich-Zeichens geschrieben.
wird auf die rechte Seite des
Istgleich-Zeichens geschrieben. - Das erste Teilergebnis wird mit
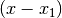 multipliziert, das Ergebnis
dieser Rechnung unter den ersten Summanden des ursprünglichen Terms
geschrieben und vom ursprünglichen Term abgezogen. Zu dem sich so ergebenden
Rest werden weitere Summanden des ursprünglichen Terms hinzugenommen.
multipliziert, das Ergebnis
dieser Rechnung unter den ersten Summanden des ursprünglichen Terms
geschrieben und vom ursprünglichen Term abgezogen. Zu dem sich so ergebenden
Rest werden weitere Summanden des ursprünglichen Terms hinzugenommen. - Das Verfahren wird so lange fortgesetzt, bis kein Rest mehr übrig bleibt.[4]
Der Restterm hat nur noch den Grad
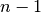 und kann üblicherweise leichter
ausgewertet werden.
und kann üblicherweise leichter
ausgewertet werden.- Zunächst wird der erste Summand
Anmerkungen:
| [1] | Siehe Abschnitt Computer-Algebra-Systeme. |
| [2] | Hierbei ist wiederum die Überlegung grundlegend, dass ein Produkt nur dann gleich Null ist, wenn (mindestens) einer der beiden Faktoren gleich Null ist. Lösungen des restlichen Terms sind somit auch Lösungen der ursprünglichen Gleichung. |
| [3] | Hierbei gilt zu beachten, dass für reelle Zahlen keine negativen
Wurzeln definiert sind. Ist 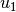 und/oder und/oder 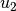 negativ, so
entfallen die entsprechenden Lösungen. negativ, so
entfallen die entsprechenden Lösungen. |
| [4] | Bliebe bei der Polynomdivision ein Rest übrig, so wäre  keine
Lösung der ursprünglichen Gleichung. keine
Lösung der ursprünglichen Gleichung. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.
