Folgen und Reihen¶
Folgen und ihre Eigenschaften¶
Ordnet man jeder natürlichen Zahl 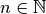 eine reelle Zahl
eine reelle Zahl
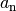 eindeutig zu, so entsteht eine unendliche (reelle) Folge
eindeutig zu, so entsteht eine unendliche (reelle) Folge
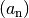 . Die einzelnen Werte der Folge heißen Folgenglieder und
werden mit Indizes durchnummeriert:
. Die einzelnen Werte der Folge heißen Folgenglieder und
werden mit Indizes durchnummeriert:
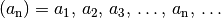
Im Unterschied zu einer Menge kann bei einer Folge ein und das selbe Glied mehrere Male auftreten. Die Definition einer Folge kann auf zweierlei Arten erfolgen:
Viele Folgen lassen sich nach einem Bildungsgesetz mittels eines Terms aufstellen. Das Bildungsgesetz wird hierzu in runde Klammern geschrieben. Beispiel:
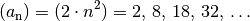
Ist (mindestens) das erste Folgenglied bekannt und besteht eine Rechenvorschrift, wie sich ein Folgenglied aus einem vorhergehenden berechnen lässt, so sind alle Glieder einer Folge ebenfalls eindeutig festgelegt. Dieses Vorgehen wird als „Rekursion“ bezeichnet. Beispiel:
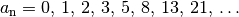
Die obige Zahlenfolge wird auch zu Ehren von Leonardo Fibonacci als „Fibonacci-Folge“ bezeichnet. Die Folgenglieder lassen sich dadurch berechnen, indem jeweils die Summe der beiden vorangehenden Folgenglieder gebildet wird. Das Bildungsgesetz der Folge lautet somit für
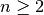 :
: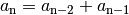
Beschränkt man die Definitionsmenge auf die ersten  natürlichen Zahlen
natürlichen Zahlen
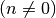 , so erhält man eine endliche Folge mit dem Anfangsglied
, so erhält man eine endliche Folge mit dem Anfangsglied
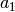 und dem Endglied
und dem Endglied 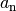 .
.
Monotonie einer Zahlenfolge¶
Ein wichtiges Kriterium bei der Unterscheidung von Zahlenfolgen ist ihre so genannte Monotonie. Werden die Werte der Folgenglieder mit zunehmendem Index kontinuierlich (wenn möglicherweise auch in unterschiedlichem Maß) größer, so nennt man die Folge monoton wachsend zunehmend. Nehmen die Werte der Folgenglieder im umgekehrten Fall kontinuierlich (möglicherweise unterschiedlich stark) ab, so spricht man von einer monoton fallenden Folge. Bei einer konstanten Folge bleiben die Werte im Verlauf der Folge konstant.
Es gilt somit für jede Folge 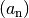 :
:
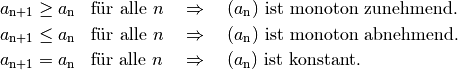
Gilt bei der obigen Unterscheidung anstelle der Kleiner-Gleich-Relation
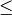 die Kleiner-Relation
die Kleiner-Relation 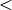 beziehungsweise anstelle der
Größer-Gleich-Relation
beziehungsweise anstelle der
Größer-Gleich-Relation 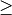 die Größer-Relation
die Größer-Relation 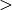 , so nennt man
die Folge streng monoton ab- beziehungsweise zunehmend.
, so nennt man
die Folge streng monoton ab- beziehungsweise zunehmend.
Beschränktheit einer Zahlenfolge¶
Eine Folge 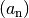 wird beschränkt genannt, wenn es zwei reelle
Zahlen
wird beschränkt genannt, wenn es zwei reelle
Zahlen  und
und 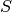 gibt, so dass die Werte aller Folgenglieder
zwischen beiden begrenzenden Zahlen liegen, wenn also gilt:
gibt, so dass die Werte aller Folgenglieder
zwischen beiden begrenzenden Zahlen liegen, wenn also gilt:
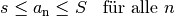
Hierbei wird  als untere Schranke und
als untere Schranke und 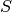 als obere Schranke
bezeichnet.
als obere Schranke
bezeichnet.
Grenzwert einer Zahlenfolge¶
Eine Folge 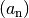 hat einen Grenzwert
hat einen Grenzwert  , wenn sich
außerhalb einer beliebig großen Umgebung von
, wenn sich
außerhalb einer beliebig großen Umgebung von  nur endlich viele Glieder
der Folge befinden. Man sagt in diesem Fall, dass der Grenzwert („Limes“) der
Folge für gegen Unendlich gehende Werte von
nur endlich viele Glieder
der Folge befinden. Man sagt in diesem Fall, dass der Grenzwert („Limes“) der
Folge für gegen Unendlich gehende Werte von  gleich
gleich  ist; in
mathematischer Kurzform schreibt man:
ist; in
mathematischer Kurzform schreibt man:
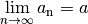
Besitzt eine Folge einen Grenzwert, so nennt man sie konvergent, andernfalls divergent.
Bezüglich des Grenzwerts einer Folge gilt:
- Der Grenzwert einer Folge ist stets eindeutig bestimmt; insbesondere ist
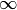 kein zulässiger Grenzwert.
kein zulässiger Grenzwert. - Jede monotone und beschränkte Folge ist konvergent, besitzt also einen (eindeutigen) Grenzwert.
- Jede konvergente Folge ist beschränkt.
Beispiele:
Die Folge
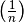 ist konvergent zum Grenzwert
ist konvergent zum Grenzwert
 , also gilt:
, also gilt: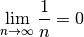
Die Folge
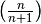 ist konvergent zum Grenzwert
ist konvergent zum Grenzwert
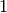 , also gilt:
, also gilt: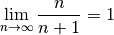
Die Folge
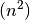 ist divergent, sie hat keinen Grenzwert.
ist divergent, sie hat keinen Grenzwert.
Folgen, die den Wert Null als Grenzwert haben, nennt man Nullfolgen. Ihnen kommt
eine besondere Bedeutung zu, denn allgemein gilt die Aussage, dass eine Folge
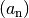 den Grenzwert
den Grenzwert  hat, wenn die Folge
hat, wenn die Folge
 eine Nullfolge ist.
eine Nullfolge ist.
Dieses Konvergenzkriterium wurde von Augustin-Louis Cauchy in eine noch nützlichere
Form gefasst, mittels derer sich die Konvergenz einer Folge auch dann nachweisen
lässt, wenn der Grenzwert  nicht schon von vornherein bekannt ist. Das
so genannte „Cauchy-Kriterium“ besagt, dass jede Folge genau dann konvergiert,
wenn sich zu jedem beliebig kleinen Wert
nicht schon von vornherein bekannt ist. Das
so genannte „Cauchy-Kriterium“ besagt, dass jede Folge genau dann konvergiert,
wenn sich zu jedem beliebig kleinen Wert  eine Zahl
eine Zahl
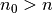 finden lässt, so dass für alle Folgenglieder
finden lässt, so dass für alle Folgenglieder
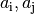 ab
ab 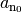 gilt, dass
gilt, dass
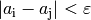 ist.
ist.
Wichtige Grenzwerte
Für die Mathematik haben unter anderem folgende Grenzwerte für  gegen
Unendlich
gegen
Unendlich  eine besondere Bedeutung:
eine besondere Bedeutung:
![\lim_{n \to \infty} \frac{a}{n} &= 0 \;\; \text{ für } a \in \mathbb{R} \\[4pt]
\lim_{n \to \infty} a^n &= 0 \;\; \text{ für } |a| < 1 \\[4pt]
\lim_{n \to \infty} \sqrt[n]{a} &= 1 \;\; \text{ für } a \in \mathbb{R}^{+} \\[4pt]
\lim_{n \to \infty} \sqrt[n]{n} &= 1 \\[4pt]
\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n &= e \\[4pt]
\lim_{n \to \infty} \left( 1 - \frac{1}{n} \right)^n &= \frac{1}{e} \\[4pt]
\lim_{n \to \infty} \left( 1 + \frac{k}{n} \right)^n &= e^{k} \\[4pt]](../_images/math/172e6f6d900744996cc64ca9b384f02a2912537d.png)
Die Zahl 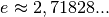 ist irrational und wird „Eulersche Zahl“
genannt; sie ist insbesondere für Exponentialfunktionen von besonderer Bedeutung.
ist irrational und wird „Eulersche Zahl“
genannt; sie ist insbesondere für Exponentialfunktionen von besonderer Bedeutung.
Arithmetische Folgen¶
Eine Folge heißt arithmetisch, wenn die Differenz  zweier aufeinander
folgender Glieder stets konstant ist. Für eine arithmetische Folge gilt also:
zweier aufeinander
folgender Glieder stets konstant ist. Für eine arithmetische Folge gilt also:

Als Bildungsgesetz gilt:
(1)¶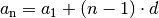
Ist 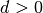 , so ist die Folge (streng) monoton steigend, bei
, so ist die Folge (streng) monoton steigend, bei 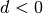 ist die Folge (streng) monoton fallend. Gilt
ist die Folge (streng) monoton fallend. Gilt 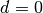 , so ist die Folge
konstant.
, so ist die Folge
konstant.
Da die einzelnen Folgenglieder immer um den gleichen Betrag zu- beziehungsweise abnehmen, ist das mittlere dreier Folgenglieder stets gleich dem arithmetischen Mittel der beiden benachbarten Folgenglieder. Es gilt also:[1]
(2)¶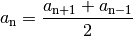
Wichtige arithmetische Folgen sind beispielsweise die natürlichen Zahlen
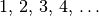 , die geraden Zahlen
, die geraden Zahlen 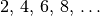 , die ungeraden Zahlen
, die ungeraden Zahlen 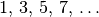 , usw.
, usw.
Will man zwischen zwei Werten 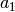 und
und 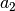 insgesamt
insgesamt  weitere Zahlen als eine arithmetische Folge einfügen, so gilt dabei für alle
Differenzen der einzelnen Folgenglieder:
weitere Zahlen als eine arithmetische Folge einfügen, so gilt dabei für alle
Differenzen der einzelnen Folgenglieder:

Diese Formel kann beispielsweise hilfreich sein, um fehlende Werte in
Wertetabellen (näherungsweise) zu ergänzen. Eine ähnliche Anwendung kann darin
bestehen,  Objekte (beispielsweise Holzbalken) in jeweils gleichem
Abstand voneinander zwischen zwei festen Grenzen
Objekte (beispielsweise Holzbalken) in jeweils gleichem
Abstand voneinander zwischen zwei festen Grenzen  und
und 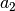 einzufügen; dabei gibt
einzufügen; dabei gibt 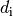 an, in welchem Abstand die
Mittelpunkte der Objekte jeweils eingefügt werden müssen.
an, in welchem Abstand die
Mittelpunkte der Objekte jeweils eingefügt werden müssen.
Geometrische Folgen¶
Eine Folge heißt geometrisch, wenn der Quotient 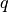 zweier aufeinander
folgender Glieder stets konstant ist. Für eine jede geometrische Folge gilt
also:
zweier aufeinander
folgender Glieder stets konstant ist. Für eine jede geometrische Folge gilt
also:
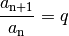
Als Bildungsgesetz gilt:
(3)¶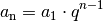
Ist 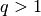 , so ist die Folge (streng) monoton zunehmend, bei
, so ist die Folge (streng) monoton zunehmend, bei 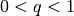 ist die Folge (streng) monoton abnehmend und konvergiert gegen Null. Gilt
ist die Folge (streng) monoton abnehmend und konvergiert gegen Null. Gilt
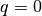 , so ist die Folge konstant, im Fall
, so ist die Folge konstant, im Fall 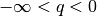 ist
die Folge „alternierend“, die Werte der Folgenglieder sind also abwechselnd
positiv und negativ.
ist
die Folge „alternierend“, die Werte der Folgenglieder sind also abwechselnd
positiv und negativ.
Da die einzelnen Folgenglieder immer um den gleichen Faktor zu- beziehungsweise abnehmen, ist das mittlere dreier Folgenglieder stets gleich dem geometrischen Mittel der beiden benachbarten Folgenglieder. Es gilt also:[2]
(4)¶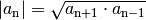
Will man zwischen zwei Werten 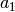 und
und 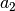 insgesamt
insgesamt  weitere Zahlen als eine geometrische Folge einfügen, so gilt dabei für alle
Quotienten der einzelnen Folgenglieder:
weitere Zahlen als eine geometrische Folge einfügen, so gilt dabei für alle
Quotienten der einzelnen Folgenglieder:
![q_{\mathrm{i}} = \sqrt[n+1]{\frac{ a_2}{ a_1}}](../_images/math/ce9739ced04b7373b689887f5091a82f1297ac85.png)
Reihen und ihre Eigenschaften¶
Die Summe der Glieder einer Folge (oder eines Teils der Folgenglieder) wird als
Reihe bezeichnet. Mathematisch wird die Summe 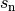 der Glieder
einer Folge
der Glieder
einer Folge 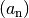 durch das Summen-Symbol
durch das Summen-Symbol 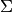 ausgedrückt:
ausgedrückt:
(5)¶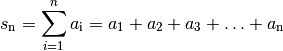
Hierbei wird unterhalb des Summenzeichens die Untergrenze und oberhalb die
Obergrenze des Index  angegeben, wobei die Summengrenzen jeweils ganze
Zahlen sind. Im obigen Fall werden alle Folgenglieder
angegeben, wobei die Summengrenzen jeweils ganze
Zahlen sind. Im obigen Fall werden alle Folgenglieder 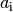 somit
von
somit
von 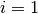 bis
bis 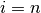 aufsummiert.
aufsummiert.
Ist die untere Summationsgrenze 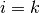 gleich der oberen, so bedeutet dies,
dass die Summe aus einer einzigen Zahl
gleich der oberen, so bedeutet dies,
dass die Summe aus einer einzigen Zahl 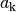 besteht:
besteht:
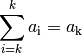
Ist die untere Summationsgrenze größer als die obere Summationsgrenze, wird das Ergebnis der Summe als Null definiert. Weitere wichtige Rechenregeln für das Summenzeichen sind:
(6)¶![\sum_{i=1}^{n} ( a_{\mathrm{i}} + b_{\mathrm{i}} ) &= \sum_{i=1}^{n} a_{\mathrm{i}}
+ \sum_{i=1}^{n} b_{\mathrm{i}} \\[4pt]
\sum_{i=1}^{n} ( a_{\mathrm{i}} - b_{\mathrm{i}} ) &= \sum_{i=1}^{n} a
_{\mathrm{i}} - \sum_{i=1}^{n} b_{\mathrm{i}} \\[4pt]
\sum_{i=i}^{n} c \cdot a_{\mathrm{i}} &= c \cdot \sum_{i=1}^{n} a
_{\mathrm{i}} \\[4pt]](../_images/math/ca74c028421bf22cfcde1b19b6e08334c152e533.png)
Die oberen beiden dieser Rechenregeln entsprechen einem Umsortieren der
Summanden, das letzte einem Ausklammern des Faktors  aus jedem
Summanden. Diese Regel findet auch Anwendung, wenn man
aus jedem
Summanden. Diese Regel findet auch Anwendung, wenn man  Folgenglieder
mit konstantem Wert aufsummiert:
Folgenglieder
mit konstantem Wert aufsummiert:
(7)¶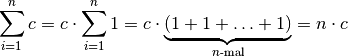
Nach der obigen Gleichung funktionieren auch digitale Zählmaschinen, die eine
Reihe von (meist elektrischen) „Eins“-Signalen aufaddieren und den
entsprechenden Wert  anzeigen.
anzeigen.
Zwei weitere Rechentricks werden im Umgang mit Reihen oftmals nutzvoll eingesetzt:
Eine Reihe lässt sich in zwei (oder mehrere) Teilsummen zerlegen. Werden in der ursprünglichen Reihe Folgenglieder von
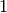 bis
bis  aufsummiert, so können in äquivalenter Weise zunächst nur die Folgenglieder
bis zu einem zwischen beiden Grenzen liegenden Wert
aufsummiert, so können in äquivalenter Weise zunächst nur die Folgenglieder
bis zu einem zwischen beiden Grenzen liegenden Wert 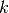 summiert werden,
und anschließend die restlichen Folgenglieder von
summiert werden,
und anschließend die restlichen Folgenglieder von  bis
bis  addiert werden.[3] Es gilt also:
addiert werden.[3] Es gilt also:(8)¶
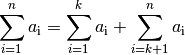
Der Wert einer Reihe bleibt durch eine Indexverschiebung unverändert. Hierunter versteht man ein Verfahren folgender Art:
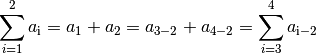
Wird der Index der Summationsgrenzen im allgemeinen Fall um
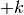 angehoben, so muss der Index der Folgenglieder auf
angehoben, so muss der Index der Folgenglieder auf  reduziert
werden.[4] Es gilt somit:
reduziert
werden.[4] Es gilt somit:(9)¶
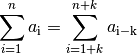
Eine Verminderung der Summationsgrenze um
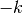 bewirkt in entsprechender
Weise eine Anhebung des Index der Folgenglieder auf
bewirkt in entsprechender
Weise eine Anhebung des Index der Folgenglieder auf 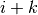 :
:(10)¶
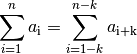
Arithmetische Reihen¶
Addiert man alle Glieder einer arithmetischen Folge, also eine Folge von Zahlen, die sich untereinander stets um den
gleichen Wert  unterscheiden, so ergibt sich eine arithmetische Reihe.
Für den Wert der wohl bekanntesten arithmetischen Reihe, bei der alle
natürlichen Zahlen von
unterscheiden, so ergibt sich eine arithmetische Reihe.
Für den Wert der wohl bekanntesten arithmetischen Reihe, bei der alle
natürlichen Zahlen von 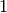 bis
bis  addiert werden, hat Carl
Friedrich Gauss bereits in jungem Alter
die folgende Formel gefunden, die bisweilen auch „Kleiner Gauss“ genannt wird:[5][6]
addiert werden, hat Carl
Friedrich Gauss bereits in jungem Alter
die folgende Formel gefunden, die bisweilen auch „Kleiner Gauss“ genannt wird:[5][6]
(11)¶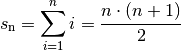
Im allgemeinen Fall lässt sich der Wert einer arithmetischen Reihe folgendermaßen berechnen:[7]
(12)¶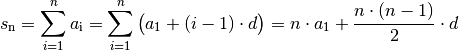
Geometrische Reihen¶
Addiert man alle Glieder einer geometrischen Folge,
also eine Folge von Zahlen, die sich untereinander stets um den gleichen Faktor
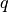 unterscheiden, so ergibt sich eine geometrische Reihe. Der Wert
unterscheiden, so ergibt sich eine geometrische Reihe. Der Wert
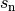 einer endlichen geometrischen Reihe lässt sich
folgendermaßen berechnen:[8]
einer endlichen geometrischen Reihe lässt sich
folgendermaßen berechnen:[8]
(13)¶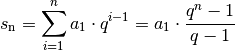
Ob eine unendliche geometrische Reihe konvergiert, hängt vom Wert von 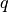 ab. Ist
ab. Ist 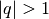 , so divergiert die Reihe; ist hingegen
, so divergiert die Reihe; ist hingegen  , so
konvergiert die Reihe, und es gilt:
, so
konvergiert die Reihe, und es gilt:
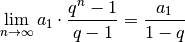
Mittels geometrischen Reihen können beispielsweise Zinseszinsen berechnet werden.
Produktfolgen¶
Neben gewöhnlichen Reihen als Summenfolgen können auch Produktfolgen gebildet
werden. In der Praxis sind jedoch meist nur so genannte Partialproduktfolgen von
Bedeutung, deren Ergebnis das Produkt von  Folgengliedern ist.
Mathematisch wird ein solches Produkt
Folgengliedern ist.
Mathematisch wird ein solches Produkt 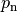 der Glieder einer
Folge
der Glieder einer
Folge 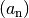 durch das Produkt-Symbol
durch das Produkt-Symbol 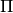 ausgedrückt:
ausgedrückt:
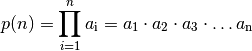
Hierbei wird unterhalb des Produktzeichens die Untergrenze und oberhalb die
Obergrenze des Index  angegeben, wobei die Produktgrenzen jeweils ganze
Zahlen sind.
angegeben, wobei die Produktgrenzen jeweils ganze
Zahlen sind.
Für die insbesondere in der Kombinatorik häufig auftretende Partialproduktfolge der natürlichen Zahlen ist eine besondere Notation üblich:
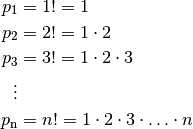
Der Ausdruck  wird dabei als „
wird dabei als „ Fakultät“ gelesen; für den
Sonderfall
Fakultät“ gelesen; für den
Sonderfall 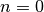 ist dabei
ist dabei 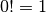 definiert.
definiert.
Anmerkungen:
| [1] | Bei einer arithmetischen Folge gilt:
Setzt man in der obigen Gleichung die linke und die rechte Seite gleich und
löst diese Gleichung nach |
| [2] | Bei einer geometrischen Folge gilt:
Setzt man in der obigen Gleichung die linke und die rechte Seite gleich und
löst diese Gleichung nach |
| [3] | Im umgekehrten Fall lässt sich eine Zerlegung in Teilsummen auch
nutzen, um den Wert einer Reihe zu berechnen, deren Glieder von
|
| [4] | Diese Ersetzung ist vorzunehmen, bevor irgendeine weitere Auswertung
erfolgt. Darauf ist insbesondere dann zu achten, wenn sich vor dem Index
 einer Reihe ein Minuszeichen befindet. Durch eine Verschiebung der
Summationsgrenzen um einer Reihe ein Minuszeichen befindet. Durch eine Verschiebung der
Summationsgrenzen um 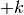 wird beispielsweise wird beispielsweise  zu zu 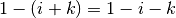 . . |
| [5] | Die Gültigkeit von Gleichung (11) wurde bereits als Beispiel im Abschnitt Die vollständige Induktion gezeigt. |
| [6] | Ähnliche Sonderfälle arithmetischer Reihen sind die Reihen der geraden und ungeraden Zahlen:
Nach der obigen Gleichung lässt sich somit jede Quadratzahl als arithmetische Reihe darstellen:
|
| [7] | Hierfür muss die Reihe zunächst aufgeteilt werden:
In der ersten Teilreihe wird der konstante Wert
Die zweite Teilreihe kann mittels einer Indexverschiebung gemäß Gleichung (10) umgeschrieben werden. Es gilt:
Nach Gleichung (11) gilt für den Wert dieser Reihe
Addiert man beide Teilreihen und berücksichtigt dabei den Faktor |
| [8] | Die Formel (13) zur Berechnung einer geometrischen Reihe kann auf zweierlei Arten dargestellt werden, denn es gilt:
Die erste Darstellung wird im Fall Um die Gültigkeit von Formel (13) zu demonstrieren,
wird die Differenz von
Auf der linken Seite kann
Löst man diese Gleichung nach |


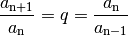
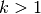 bis
bis 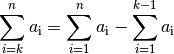
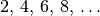 lässt sich als
lässt sich als 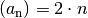 ausdrücken. Für die
entsprechende Reihe
ausdrücken. Für die
entsprechende Reihe 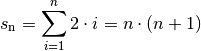
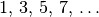 lässt sich als
lässt sich als  ausdrücken. Für die
entsprechende Reihe
ausdrücken. Für die
entsprechende Reihe 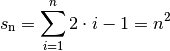
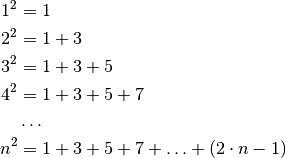
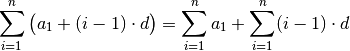
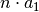 . Bei der zweiten Teilreihe kann der konstante
Faktor
. Bei der zweiten Teilreihe kann der konstante
Faktor 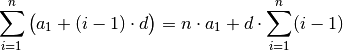
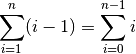

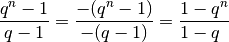
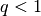 genutzt.
genutzt.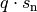 betrachtet. Es gilt:
betrachtet. Es gilt:![s_{\mathrm{n}} &= a_1 \cdot (1 + q + q^2 + q^3 + \ldots + q ^{n-1})
\\[2pt]
q \cdot s_{\mathrm{n}} &= a_1 \cdot (q + q^2 + q^3 + q^4 + \ldots + q
^{n}) \\[5pt]
\Rightarrow s_{\mathrm{n}} - q \cdot s_{\mathrm{n}} &= a_1 \cdot ( 1 +
q + q^2 + q^3 + \ldots + q ^{n-1} \\ & \phantom{ = a_1 \cdot ( 1 \,} - q
- q^2 - q^3 - \ldots - q ^{n-1} - q^n) \\](../_images/math/e62e15098a2bb53847dc8f031c0ae8fc3164a399.png)
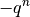 auf. Folglich gilt:
auf. Folglich gilt: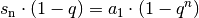
 ,
was nach der ersten Gleichung dieser Anmerkung mit Formel
,
was nach der ersten Gleichung dieser Anmerkung mit Formel