Logik¶
Die (Aussagen-)Logik ist für sämtliche Teilbereiche der Mathematik von grundlegender Bedeutung.
Satz und Aussage¶
Lässt sich einem Satz 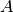 ein Wahrheitswert (
ein Wahrheitswert (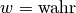 oder
oder
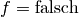 ) eindeutig zuordnen, so wird dieser Satz zu einer
Aussage.
) eindeutig zuordnen, so wird dieser Satz zu einer
Aussage.
Als Darstellungsform für den Wahrheitswert von Aussagen wählt man häufig so genannte „Wahrheitstafeln“. Dabei werden spaltenweise die Wahrheitswerte der in der Kopfzeile angegebenen Aussage(n) aufgelistet.
 |
 |
 |
Beispiele:
- Der Satz „
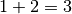 “ ist eine wahre Aussage.
“ ist eine wahre Aussage. - Der Satz „
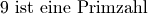 “ ist eine falsche Aussage.
“ ist eine falsche Aussage. - Der Satz „
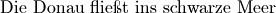 “ ist eine wahre
Aussage.
“ ist eine wahre
Aussage. - Der Satz „
 “ ist keine Aussage, da ihm kein
Wahrheitswert zugeordnet werden kann.
“ ist keine Aussage, da ihm kein
Wahrheitswert zugeordnet werden kann.
Ein Satz ist auch dann eine Aussage, wenn sein Wahrheitswert zum gegebenen Zeitpunkt nicht feststellbar ist. Beispielsweise handelt es sich bei dem Satz „Am 3. April 1650 regnete es in Berlin.“ ebenfalls um eine Aussage, auch wenn sich ihr Wahrheitswert mit großer Wahrscheinlichkeit nicht mehr feststellen lässt.
Negation einer Aussage
Durch Verneinen einer Aussage 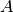 entsteht eine Aussage
entsteht eine Aussage 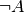 ,
die Negation der Aussage
,
die Negation der Aussage 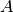 genannt wird. Da der konkrete Wahrheitswert
einer negierten Aussage
genannt wird. Da der konkrete Wahrheitswert
einer negierten Aussage 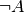 stets vom Wahrheitswert der eigentlichen
Aussage
stets vom Wahrheitswert der eigentlichen
Aussage 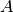 abhängt, hat die entsprechende Wahrheitstafel zwei Spalten.
abhängt, hat die entsprechende Wahrheitstafel zwei Spalten.
 |
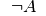 |
 |
 |
 |
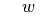 |
Die Negation einer wahren Aussage ist falsch, die einer falschen ist wahr;
insbesondere entspricht die doppelte Negation einer Aussage 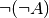 der ursprünglichen Aussage
der ursprünglichen Aussage 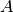 .
.
Beispiele:
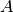 : „Die Geraden
: „Die Geraden 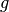 und
und 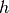 schneiden sich.“
schneiden sich.“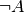 : „Die Geraden
: „Die Geraden 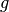 und
und 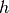 schneiden sich nicht.“
schneiden sich nicht.“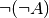 : „Es ist nicht wahr, dass die Geraden
: „Es ist nicht wahr, dass die Geraden 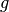 und
und
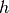 sich nicht schneiden.“
sich nicht schneiden.“
Verknüpfungen von Aussagen¶
Mit Hilfe von Bindewörtern wie „und“, „oder“, „genau dann, wenn“ usw. lassen sich mehrere (Teil-)Aussagen zu einer zusammengesetzten Aussage verknüpfen. In der Logik lassen sich mit Hilfe der folgenden Aussage-Funktionen zwei (oder mehrere) Aussagen zu einer neuen Aussage formen.
Die Konjunktion
Verknüpft man zwei Aussagen 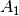 und
und 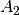 durch
das Wort „und“, so entsteht die Konjunktion der Aussagen
durch
das Wort „und“, so entsteht die Konjunktion der Aussagen 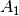 und
und
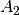 , symbolisch mit
, symbolisch mit 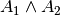 bezeichnet.
bezeichnet.
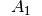 |
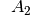 |
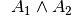 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Eine Konjunktion zweier Aussagen ist somit nur wahr, wenn beide (Teil-)Aussagen wahr sind.
Beispiele:
- Die Konjunktion der wahren Aussage
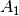 „
„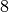 ist eine gerade
Zahl“ mit der falschen Aussage
ist eine gerade
Zahl“ mit der falschen Aussage 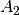 „
„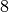 ist durch
ist durch 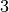 teilbar“ ist die falsche Aussage
teilbar“ ist die falsche Aussage 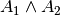 : „
: „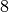 ist eine
gerade Zahl und durch
ist eine
gerade Zahl und durch 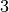 teilbar“.
teilbar“. - Die falsche Aussage „Der Mars ist ein Gasplanet und hat eine größere Masse als die Erde“ ist eine Konjunktion der falschen Aussagen „Der Mars ist ein Gasplanet“ und „Der Mars hat eine größere Masse als die Erde“.
Die Adjunktion
Verknüpft man zwei Aussagen 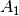 und
und 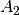 durch das Wort „oder“,
so entsteht die Adjunktion der Aussagen
durch das Wort „oder“,
so entsteht die Adjunktion der Aussagen 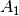 und
und 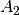 , symbolisch
mit
, symbolisch
mit 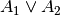 bezeichnet.
bezeichnet.
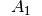 |
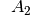 |
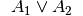 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Die Adjunktion ist somit wahr, wenn eine der beiden Aussagen wahr ist (oder beide wahr sind).
Beispiele:
- Die Adjunktion der wahren Aussage
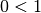 und der falschen Aussage
und der falschen Aussage
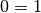 ist die wahre Aussage
ist die wahre Aussage 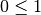 .
. - Die wahre Aussage: „Entweder ist die Erde ein Würfel oder die Sonne ist ein Stern“ ist eine Adjunktion der falschen Aussage: „Die Erde ist ein Würfel“ und der wahren Aussage: „Die Sonne ist ein Stern“.
Die Implikation
Verknüpft man zwei Aussagen 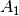 und
und 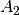 durch das Wort „dann“,
so entsteht die Implikation der Aussagen
durch das Wort „dann“,
so entsteht die Implikation der Aussagen 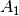 und
und 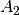 , symbolisch
mit
, symbolisch
mit 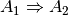 bezeichnet.
bezeichnet.
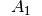 |
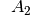 |
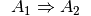 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Die Implikation ist wahr, wenn beide Aussagen 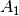 und
und 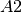 wahr sind oder wenn die erste Aussage
wahr sind oder wenn die erste Aussage 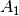 falsch ist.[1]
Formal erhält man eine identische Wahrheitstafel, wenn man die Implikation
falsch ist.[1]
Formal erhält man eine identische Wahrheitstafel, wenn man die Implikation
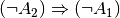 bildet.[2][3]
bildet.[2][3]
Beispiele:
- Die Aussage „Wenn
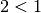 ist, dann ist
ist, dann ist 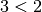 “ ist wahr,
obwohl sie eine Implikation zweier falscher (Teil-)Aussagen ist.
“ ist wahr,
obwohl sie eine Implikation zweier falscher (Teil-)Aussagen ist. - Die Implikation der wahren Aussage „Die Lichtgeschwindigkeit beträgt annähernd
![\unit[300\,000]{km/s}](_images/math/6b61dde2ea3467b0387ad603e937ffa088acaaab.png) “ und der falschen Aussage „Die
Schallgeschwindigkeit ist größer als die Lichtgeschwindigkeit“ ist die falsche
Aussage „Die Schallgeschwindigkeit beträgt mehr als
“ und der falschen Aussage „Die
Schallgeschwindigkeit ist größer als die Lichtgeschwindigkeit“ ist die falsche
Aussage „Die Schallgeschwindigkeit beträgt mehr als
![\unit[300\,000]{km/s}](_images/math/6b61dde2ea3467b0387ad603e937ffa088acaaab.png) „.
„.
Äquivalenz zweier Aussagen
Verknüpft man zwei Aussagen 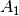 und
und 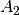 durch die
Wortkombination „dann, und nur dann“, so entsteht die Äquivalenz der Aussagen
durch die
Wortkombination „dann, und nur dann“, so entsteht die Äquivalenz der Aussagen
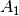 und
und 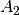 , symbolisch mit
, symbolisch mit 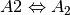 bezeichnet.
bezeichnet.
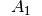 |
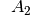 |
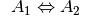 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Die Äquivalenz zweier Teilaussagen ist nur wahr, wenn entweder beide Teilaussagen wahr oder beide falsch sind.[4]
Beispiele:
- Die wahre Aussage „Im rechtwinkligen Dreieck gilt der Höhensatz“ äquivalent verknüpft mit der falschen Aussage „Im rechtwinkligen Dreieck sind alle Seiten gleich lang“ ergibt die falsche Aussage „Im rechtwinkligen Dreieck sind dann und nur dann alle Seiten gleich lang, wenn der Höhensatz gilt“.
- Die Äquivalenzverknüpfung der falschen Aussage „Das Kilogramm ist eine Längeneinheit“ mit der wahren Aussage „Tausend Meter ergeben einen Kilometer“ ist die falsche Aussage „Das Kilogramm ist dann und nur dann eine Längeneinheit, wenn tausend Meter einen Kilometer ergeben“.
Kontravalenz zweier Aussagen
Verknüpft man zwei Aussagen 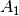 und
und 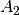 durch das Wort „entweder
oder“ im ausschließenden Sinn, so entsteht die Kontravalenz der Aussagen
durch das Wort „entweder
oder“ im ausschließenden Sinn, so entsteht die Kontravalenz der Aussagen
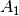 und
und 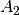 , mit mit
, mit mit 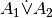 bezeichnet.
bezeichnet.
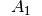 |
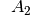 |
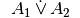 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Die Kontravalenz zweier Teilaussagen ist nur dann wahr, wenn genau eine der beiden (Teil-)Aussagen wahr ist. Damit ist sie formal, wie ihr Name bereits andeutet, mit der Negation der Äquivalenz identisch.
Beispiel:
- Verknüpft man die wahre Aussage „Der Zug fährt nach München“ kontravalent mit der falschen Aussage „Der Zug fährt nach Frankfurt“, so ergibt sich die wahre Aussage „Der Zug fährt entweder nach München oder nach Frankfurt“.
Regeln zu den Aussagenverknüpfungen
Zwischen den Aussagen beziehungsweise ihren Verknüpfungen sind folgende Äquivalenzen definiert, von denen einige eine formale Ähnlichkeit mit den Regeln für das Rechnen mit Zahlen haben:
- Kommutativgesetz:
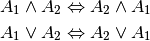
- Assoziativgesetz:
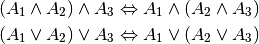
- Distributivgesetz:
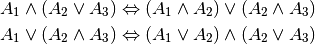
Hinzu kommen folgende Regeln, die bisweilen für Beweisverfahren sowie in der Informatik nützlich sind:
- Regeln von de Morgan:
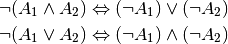
- Absorptionsgesetz:
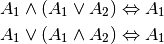
- Idempotenzgesetz:
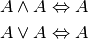
- Komplementgesetz:
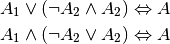
Dabei wird die Verknüpfung 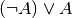 auch „Tautologie“ genannt;
sie ist stets wahr.[5]
auch „Tautologie“ genannt;
sie ist stets wahr.[5]
Variablen, Terme und Aussageformen¶
Eine Variable ist ein Symbol für ein beliebiges Element aus einer vorgegebenen Grundmenge. Darüber hinaus gelten für das Rechnen mit Variablen keine besonderen Regeln oder Gesetze.
Ein Term ist eine Bezeichnung zum einen für ein einzelnes mathematisches Objekt
(beispielsweise 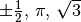 ), zum anderen auch für eine
Aneinanderreihung mehrerer Konstanten, Variablen, Klammern und Rechenoperatoren
(beispielsweise
), zum anderen auch für eine
Aneinanderreihung mehrerer Konstanten, Variablen, Klammern und Rechenoperatoren
(beispielsweise 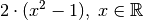 ).[6] Terme enthalten
allerdings kein Relationszeichen, sie sind somit weder wahr noch falsch.
).[6] Terme enthalten
allerdings kein Relationszeichen, sie sind somit weder wahr noch falsch.
Eine Aussageform enthält neben (mindestens) einer Variablen und (mindestens)
einem Term stets ein Relationszeichen – beispielsweise 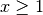 oder
oder
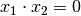 . Um allerdings einer Aussageform auch einen
Wahrheitswert zuordnen zu können, müssen zunächst alle auftretenden Variablen
durch konkrete Elemente aus der Grundmenge ersetzt werden. Ebenso wie Aussagen
lassen sich mehrere Aussageformen durch logische Verknüpfungen zu neuen
Aussageformen kombinieren.
. Um allerdings einer Aussageform auch einen
Wahrheitswert zuordnen zu können, müssen zunächst alle auftretenden Variablen
durch konkrete Elemente aus der Grundmenge ersetzt werden. Ebenso wie Aussagen
lassen sich mehrere Aussageformen durch logische Verknüpfungen zu neuen
Aussageformen kombinieren.
Die Abhängigkeit einer Aussageform von einer oder mehreren Variablen 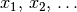 wird in der Form
wird in der Form 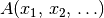 ausgedrückt. Dabei lassen sich Aussageformen in drei Arten unterteilen:
ausgedrückt. Dabei lassen sich Aussageformen in drei Arten unterteilen:
- Wird eine von einer Variablen
 abhängige Aussageform
abhängige Aussageform 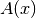 für
jedes beliebige
für
jedes beliebige  aus einer Grundmenge
aus einer Grundmenge 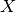 erfüllt, so
bezeichnet man die Aussageform
erfüllt, so
bezeichnet man die Aussageform 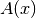 als allgemeingültig bezüglich
als allgemeingültig bezüglich
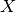 .
. - Existiert mindestens ein
 aus der Grundmenge
aus der Grundmenge 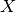 , das die
Aussageform
, das die
Aussageform 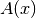 erfüllt, so bezeichnet man die Aussageform
erfüllt, so bezeichnet man die Aussageform 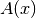 als
erfüllbar bezüglich
als
erfüllbar bezüglich 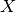 .
. - Existiert kein
 aus der Grundmenge
aus der Grundmenge 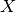 , das die Aussageform
, das die Aussageform
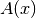 erfüllt, so bezeichnet man die Aussageform
erfüllt, so bezeichnet man die Aussageform 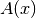 als
unerfüllbar bezüglich
als
unerfüllbar bezüglich 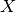 .
.
Aussageformen werden insbesondere in der Algebra als Gleichungen und Ungleichungen behandelt.
‚Für alle‘ und ‚Es gibt‘
Aussageformen können – neben dem Einsetzen von konkreten Objekten für die auftretenden Variablen – auch auf eine zweite Art und Weise zu Aussagen gemacht werden: Der Quantifizierung.
Eine allgemeine Aussageform
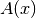 wird zu einer „Existenz-Aussage“,
wenn folgende Forderung erfüllt ist:
wird zu einer „Existenz-Aussage“,
wenn folgende Forderung erfüllt ist:„Es existiert (mindestens) ein Element
 aus der Grundmenge
aus der Grundmenge
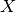 „, für das die Aussageform
„, für das die Aussageform 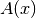 wahr ist.“
wahr ist.“Verkürzend kann eine Existenz-Aussage mit Hilfe des so genannten „Existenz-Quantors“
 formuliert werden: Anstelle von „Es
existiert (mindestens) ein
formuliert werden: Anstelle von „Es
existiert (mindestens) ein  “ kann auch kurz
“ kann auch kurz 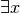 geschrieben werden.
geschrieben werden.Eine allgemeine Aussageform
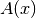 wird zu einer „Universal-Aussage“,
wenn folgende Forderung erfüllt ist:
wird zu einer „Universal-Aussage“,
wenn folgende Forderung erfüllt ist:„Für jedes Element
 aus der Grundmenge
aus der Grundmenge 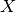 “ ist die
Aussageform
“ ist die
Aussageform 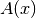 wahr.“
wahr.“Verkürzend kann eine Universal-Aussage mit Hilfe des so genannten „All-Quantors“
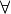 formuliert werden: Anstelle von „Für alle
formuliert werden: Anstelle von „Für alle
 “ kann auch kurz
“ kann auch kurz 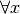 geschrieben werden.
geschrieben werden.
Während eine Existenz-Aussage 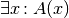 wahr ist, wenn die
zugrunde liegende Aussageform
wahr ist, wenn die
zugrunde liegende Aussageform 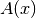 auch nur für ein konkretes
auch nur für ein konkretes  erfüllt wird, so kann im umgekehrten Fall eine Universal-Aussage
erfüllt wird, so kann im umgekehrten Fall eine Universal-Aussage 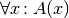 bereits durch den Existenz-Nachweis eines einzigen „Gegenbeispiels“
bereits durch den Existenz-Nachweis eines einzigen „Gegenbeispiels“
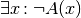 als falsch widerlegt werden.[7][8]
als falsch widerlegt werden.[7][8]
Direkte und indirekte Beweise¶
Die formalen Regeln der Logik können auch genutzt werden, um mittels bereits als wahr nachgewiesener Aussageformen Schlussfolgerungen auf neue Gesetzmäßigkeiten ziehen zu können. Auf diese Art gewonnene Lehrsätze (auch „Theoreme“ oder kurz „Sätze“ genannt) stellen das Grundgerüst der mathematischen Theorie dar.
Neben bereits bekannten Lehrsätzen werden auch so genannte Definitionen genutzt,
um neue Sätze beweisen zu können. Beim Definieren wird ein Begriff durch die
Festlegung wesentlicher, gemeinsamer Merkmale eindeutig bestimmt und von anderen
Begriffen unterschieden. Definitionen sind weder wahr noch falsch, sie dienen
vielmehr als Abkürzungen für unhandliche Formulierungen. Als Definitionszeichen
für mathematische Terme verwendet man das Zeichen  , eine
Kurzschreibweise für „ist nach Definition gleich“.
, eine
Kurzschreibweise für „ist nach Definition gleich“.
Für die eigentlichen „Beweise“ sind u.a. folgende aussagenlogische Schlussregeln möglich:
- Schlussfolgerung aus einer Implikation:
- Gilt eine Aussage
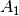 und ist die Implikation
und ist die Implikation 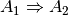 wahr, so ist auch
wahr, so ist auch 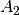 eine wahre Aussage. Kurz formuliert ist
somit der aussagenlogische Ausdruck
eine wahre Aussage. Kurz formuliert ist
somit der aussagenlogische Ausdruck ![[ A_1 \wedge (A_1 \Rightarrow
A_2)] \Rightarrow A_2](_images/math/d308bb0f9c1ab783e105ad1987720b0bd8ae7952.png) allgemeingültig.
allgemeingültig.
- Schlussfolgerung aus einer Negation:
- Der aussagenlogische Ausdruck
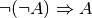 ist
allgemeingültig. Eine Aussage kann somit bewiesen werden, indem man die
Negation der Aussage widerlegt.
ist
allgemeingültig. Eine Aussage kann somit bewiesen werden, indem man die
Negation der Aussage widerlegt.
Bei direkten Beweisen wird, ausgehend von gültigen Voraussetzungen und unter Verwendung von zulässigen Schlussregeln, nach endlich vielen Schritten direkt auf die Behauptung gefolgert. Bei indirekten Beweisen hingegen wird die Negation der Behauptung zu den Voraussetzungen hinzugenommen.
Die vollständige Induktion
Die vollständige Induktion ist ein häufig genutztes Verfahren zum direkten Beweisen einer Aussage. Die logische Schlussfolgerung beruht dabei auf drei Schritten:
- Mit dem „Induktionsanfang“ wird gezeigt, dass eine Aussageform
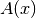 für ein (beliebig wählbaren) Wert
für ein (beliebig wählbaren) Wert  gültig ist.
gültig ist. - Die „Induktionsannahme“ besteht darin, dass die Aussageform
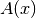 für
ein bestimmtes
für
ein bestimmtes  gültig ist.
gültig ist. - Mit dem „Induktionsschluss“, einem „Beweis im Beweis“, wird gezeigt, dass aus
der Gültigkeit der Aussage
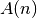 auch die Gültigkeit der Aussage
auch die Gültigkeit der Aussage
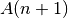 folgt, in Kurzschreibweise
folgt, in Kurzschreibweise 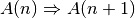 .
.
Beispiel:
Mit Hilfe der vollständigen Induktion soll bewiesen werden, dass für alle natürlichen Zahlen
 gilt:
gilt: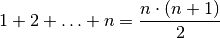
- Induktionsanfang: Für
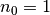 gilt:
gilt:
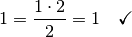
- Induktionsannahme: Für eine beliebige Zahl
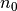 gilt die
Aussageform
gilt die
Aussageform
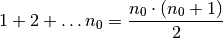
- Induktionsschluss:
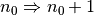
![1 + 2 + \ldots + n_0 + (n_0 + 1)
&= \frac{n_0
\cdot (n_0 + 1)}{2} + (n_0 + 1) \\[4pt]
&= \frac{1}{2} \cdot n_0 \cdot (n_0 + 1) + (n_0
+ 1) = (n_0 + 1) \cdot \left( \frac{1}{2} \cdot n_0 + 1 \right) \\[6pt]
&= (n_0 + 1) \cdot \frac{1}{2} \cdot (n_0 + 2) = \frac{(n
_0 + 1) \cdot (n_0 + 2)}{2} \\[6pt]
&= \frac{(n_0 + 1) \cdot ((n_0 + 1) + 1)}{2} \quad
\checkmark](_images/math/ea08be22350597d2f97e637837b1788f2c37bf48.png)
Aus der Richtigkeit der Aussageform für
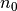 folgt somit auch
die Richtigkeit der Annahme für
folgt somit auch
die Richtigkeit der Annahme für 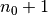 . Somit ist die
Aussageform für alle
. Somit ist die
Aussageform für alle 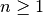 wahr.
wahr.- Induktionsanfang: Für
Anmerkungen:
| [1] | Der letztere Fall wird bisweilen auch als „Ex falso quodlibet“ bezeichnet – aus einer falschen Annahme folgt Beliebiges. |
| [2] | Die vorschnelle Annahme, dass aus Ein anschauliches Beispiel hierfür ist die Aussage Man sagt daher auch, dass |
| [3] | Es existiert sogar eine dritte Darstellungsweise der Implikation, und
zwar 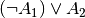 . Dies lässt anhand der
Wahrheitstabelle der Adjunktion überprüfen, indem
man für . Dies lässt anhand der
Wahrheitstabelle der Adjunktion überprüfen, indem
man für 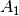 die jeweils entgegengesetzten Wahrheitswerte annimmt und
das Ergebnis der so gebildeten Adjunktion mit der Wahrheitstabelle der
Implikation vergleicht. die jeweils entgegengesetzten Wahrheitswerte annimmt und
das Ergebnis der so gebildeten Adjunktion mit der Wahrheitstabelle der
Implikation vergleicht. |
| [4] | Formal erhält man eine identische Wahrheitstafel, wenn man die beiden
Implikationen
|
| [5] | Das Gegenteil der Tautologie, die Aussage 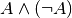 ,
heißt Kontradiktion; sie ist für jede beliebige Aussagen ,
heißt Kontradiktion; sie ist für jede beliebige Aussagen 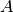 stets
falsch. stets
falsch. |
| [6] | Setzt man für die in Termen auftretenden Variablen konkrete mathematische
Objekte des Grundbereichs ein, so ergibt sich ein neuer mathematischer
Ausdruck; beispielsweise ergibt der Term 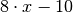 für für 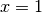 den Wert den Wert 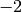 . . |
| [7] | In Zusammenhang mit den Quantoren  und und 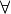 stellt der folgende Doppelpunkt
stellt der folgende Doppelpunkt : eine Kurzschreibweise für „so dass
gilt:“ beziehungsweise „gilt:“ dar. |
| [8] | Auch kombinierte Quantifizierungs-Aussagen sind möglich, beispielsweise
„Für jeden Menschen 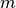 existiert ein Tag existiert ein Tag 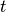 , so dass die
Aussageform , so dass die
Aussageform 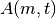 erfüllt ist: erfüllt ist: 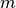 hat am Tag hat am Tag 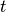 Geburtstag“. Als Kurzform kann für diese (wahre) Aussage
Geburtstag“. Als Kurzform kann für diese (wahre) Aussage 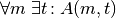 geschrieben werden. geschrieben werden. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

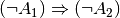 folge, ist hingegen falsch.
folge, ist hingegen falsch.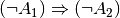 würde lauten „Wenn es nicht regnet, dann ist es
nicht bewölkt“, was offensichtlich falsch ist. Die Aussage
würde lauten „Wenn es nicht regnet, dann ist es
nicht bewölkt“, was offensichtlich falsch ist. Die Aussage 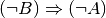 „Wenn es nicht bewölkt ist, dann regnet es nicht“ ist
hingegen richtig.
„Wenn es nicht bewölkt ist, dann regnet es nicht“ ist
hingegen richtig.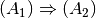 und
und 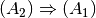 bildet und durch eine Konjunktion miteinander verknüpft. Es gilt
also:
bildet und durch eine Konjunktion miteinander verknüpft. Es gilt
also: