Zinsrechnung¶
Ein Anwendungsbeispiel für geometrische Reihen ist die Zinsrechnung. Unter Zinsen versteht man allgemein einen Betrag, der für das Überlassen einer Geldmenge („Kapital“) innerhalb einer bestimmten Zeit („Zinsperiode“, üblicherweise ein Kalenderjahr) zu bezahlen ist.
Die Höhe der Zinsen ist von drei Größen abhängig: Der überlassenen Geldmenge
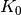 , der Dauer
, der Dauer 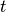 der Überlassung („Laufzeit“), und dem so
genannten Zinssatz
der Überlassung („Laufzeit“), und dem so
genannten Zinssatz 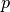 . Der Zinssatz gibt prozentual den Anteil an Geld
an, der am Ende einer Zinsperiode bezahlt werden muss.
. Der Zinssatz gibt prozentual den Anteil an Geld
an, der am Ende einer Zinsperiode bezahlt werden muss.
In der Bankenpraxis entspricht ein Jahr 360 Tagen beziehungsweise jeder Monat 30
Tagen. Bezeichnet man man bei kürzeren Zeiträumen als einem Jahr die Zahl der
Zinstage mit  , so gilt
, so gilt 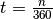 .
.
Einfache Verzinsung¶
Bei einer einfachen Verzinsung werden die Zinsen am Ende einer Zinsperiode ausgezahlt; sie werden in den folgenden Perioden somit nicht weiter mit verzinst. Das Kapital wächst in diesem Fall linear mit der Zeit an.
Mit einer einfachen Verzinsung wird in der Praxis vor allem dann gerechnet, wenn der Zeitraum zwischen den Zinszahlungen kürzer als eine Zinsperiode ist.
Die nach der Zeit 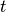 anfallenden Zinsen
anfallenden Zinsen 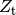 werden
folgendermaßen berechnet:
werden
folgendermaßen berechnet:
(1)¶![Z_{\mathrm{t}} &= K_0 \cdot p \cdot t \\[5pt]](../_images/math/0c833fae31a95a3004ea88a317065a2b16f76f6d.png)
Die Zeit 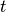 wird dabei als Bruchteil oder Vielfaches der Zinsperiode
angegeben. Die Zinsen
wird dabei als Bruchteil oder Vielfaches der Zinsperiode
angegeben. Die Zinsen 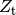 werden am Ende einer Zinsperiode dem
Kapital aufaddiert:
werden am Ende einer Zinsperiode dem
Kapital aufaddiert:
(2)¶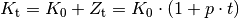
Beispiele:
Eine Kapital
![K_0=\unit[2000]{Eur}](../_images/math/9f0562a6f5cd7479d23be801b38d63eb6bdc8c2f.png) wird am 1. März eines Jahres zu
einem jährlichen Zinssatz von
wird am 1. März eines Jahres zu
einem jährlichen Zinssatz von 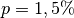 auf eine Bank eingezahlt und am 1.
September wieder abgehoben. Auf welchen Betrag
auf eine Bank eingezahlt und am 1.
September wieder abgehoben. Auf welchen Betrag 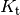 hat das
Kapital in diesem Fall zugenommen?
hat das
Kapital in diesem Fall zugenommen?Das Kapital wird für sechs Monate, also
![\unit[180]{Tage}](../_images/math/31317d88147f5e5f2a55e63c444f8396d2a54384.png) beziehungsweise
beziehungsweise ![t=\unit[\frac{180}{360}]{Jahr}](../_images/math/afb689183f5d032dea7092b23fbc32e9699b0245.png) verzinst. Für den
Betrag der Zinsen gilt mit
verzinst. Für den
Betrag der Zinsen gilt mit ![K_0=\unit[2000]{Eur}](../_images/math/9f0562a6f5cd7479d23be801b38d63eb6bdc8c2f.png) und
und 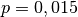 :
:![Z_{\mathrm{t}} = K_0 \cdot p \cdot t = \unit[2000]{Eur} \cdot 0,015 \cdot
\frac{180}{360} = \unit[15]{Eur}](../_images/math/a1ee20fa2cde3bdf1db60241a0b526ee89ce1e1a.png)
Das Kapital beträgt am Ende somit
![\unit[(2000 + 15)]{Eur}](../_images/math/26c95c7a1177450a7223cfce9f2d75c917692f67.png) .
.Eine Geldmenge von
![K_0 = \unit[10\,000]{Eur}](../_images/math/c3ef889cafb79d3cb4cbe4136729a7f120d37d26.png) wird für
wird für
![t=\unit[1]{Jahr}](../_images/math/c37614501da61d0af41b090becbfdff325b817b0.png) zu einem jährlichen Zinssatz von
zu einem jährlichen Zinssatz von 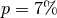 von
einer Bank geliehen. Wie viel Geld muss am Ende des Jahres zurück gezahlt
werden?
von
einer Bank geliehen. Wie viel Geld muss am Ende des Jahres zurück gezahlt
werden?Für den Betrag an Zinsen gilt mit
![K_0=\unit[10\,000]{Eur}](../_images/math/752ba9ab69ad1403b5ddd626ebe50649a2996da7.png) ,
,
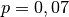 und
und 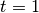 :
:![Z_{\mathrm{t}} = K_0 \cdot p \cdot t = \unit[10\,000]{Eur} \cdot 0,07 \cdot
1 = \unit[700]{Eur}](../_images/math/ef0ac89312e30b43a1a86864e0f44f67df0f557d.png)
Am Endes des Jahres müssen somit
![\unit[(10\,000 + 700)]{Eur}](../_images/math/1b91ce8e6083267860ca6cf1b8ad76153dcf64fe.png) gezahlt
werden.
gezahlt
werden.
Barwertvergleich
Das Endkapital 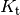 nach der Zeit
nach der Zeit 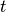 wird auch als
Zeitwert bezeichnet; entsprechend wird der Kapitalwert
wird auch als
Zeitwert bezeichnet; entsprechend wird der Kapitalwert 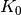 zum Zeitpunkt
zum Zeitpunkt
 auch Barwert genannt. Kennt man das Endkapital
auch Barwert genannt. Kennt man das Endkapital 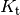 zu einem Zeitpunkt
zu einem Zeitpunkt 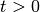 , so kann nach Umstellung der obigen Formel auch
der zugrunde liegende Barwert berechnet werden:
, so kann nach Umstellung der obigen Formel auch
der zugrunde liegende Barwert berechnet werden:
(3)¶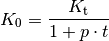
Ein so genannter Barwertvergleich kann insbesondere genutzt werden, wenn
Zahlungen zu unterschiedlichen Zeitpunkten miteinander verglichen werden sollen.
In diesem Fall bezieht man üblicherweise alle Zahlungen auf den Zeitpunkt
 .
.
Beispiel:
Eine Rechnung kann entweder innerhalb von
![\unit[7]{Tagen}](../_images/math/5dc60a47720eea1e8606e984e3e88ac922ab7c71.png) mit
mit
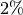 Preisnachlass („Skonto“) oder innerhalb von
Preisnachlass („Skonto“) oder innerhalb von
![\unit[30]{Tagen}](../_images/math/b31930da245da5be8a31495fda498257464a6ef1.png) ohne Preisnachlass gezahlt werden. Welchem Zinssatz
entspräche hierbei eine Zahlung nach
ohne Preisnachlass gezahlt werden. Welchem Zinssatz
entspräche hierbei eine Zahlung nach ![\unit[5]{Tagen}](../_images/math/5faab11241d485431e50eb92c2fe7290531f793d.png) ?
?Bei einer sofortigen Zahlung muss bei
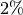 Skonto ein Kapital von
Skonto ein Kapital von
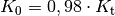 aufgebracht werden; die Zeitdifferenz
zwischen einer Zahlung nach
aufgebracht werden; die Zeitdifferenz
zwischen einer Zahlung nach 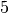 und nach
und nach 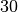 Tagen beträgt
Tagen beträgt
![\unit[25]{T}](../_images/math/edf9f288082dd92c9215eec4be634523b15a3a3e.png) , also ist
, also ist 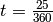 . Somit gilt:
. Somit gilt: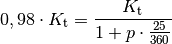
Multipliziert man diese Gleichung mit dem Nenner der rechten Seite und dividiert durch
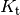 , so ergibt sich folgende Gleichung:
, so ergibt sich folgende Gleichung: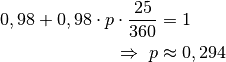
Der Preisnachlass entspricht, bezogen auf den angegebenen Zeitraum, somit einem Zinssatz von etwa
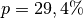 .
.
Zinseszinsrechnung¶
Werden die Zinsen nach einer Zinsperiode weiter verzinst, so entstehen so genannte Zinseszinsen.
Nach einer Zinsperiode ist das ursprüngliche Kapital 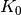 entsprechend
der einfachen Verzinsung um die Zinsmenge
entsprechend
der einfachen Verzinsung um die Zinsmenge 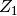 auf den Betrag
auf den Betrag
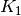 angewachsen. Es gilt also:
angewachsen. Es gilt also:
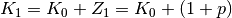
Im zweiten Jahr wird das Kapital 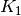 verzinst. Für die sich ergebenden
Zinsen
verzinst. Für die sich ergebenden
Zinsen 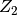 beziehungsweise das Kapital
beziehungsweise das Kapital 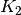 nach zwei Jahren
gilt:
nach zwei Jahren
gilt:
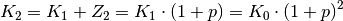
Der Faktor 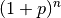 wird Aufzinsungsfaktor oder kurz Zinsfaktor genannt
und häufig auch mit
wird Aufzinsungsfaktor oder kurz Zinsfaktor genannt
und häufig auch mit 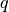 bezeichnet. Nach
bezeichnet. Nach  Jahren Laufzeit ergibt
sich damit eine Zins- beziehungsweise Kapitalmenge:
Jahren Laufzeit ergibt
sich damit eine Zins- beziehungsweise Kapitalmenge:
(4)¶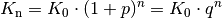
Diese nach dem Mathematiker Gottfried Wilhelm Leibniz benannte Zinseszinsformel entspricht formal einer geometrischen Reihe.
Ebenso wie bei der einfachen Verzinsung kann bei einem bekannten Zinssatz
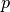 und einer gegebenen Laufzeit
und einer gegebenen Laufzeit 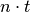 auf das Anfangskapital
auf das Anfangskapital
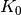 geschlossen werden, wenn das Endkapital
geschlossen werden, wenn das Endkapital 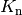 bekannt
ist. Als Barwert-Formel der Zinseszinsrechung ergibt sich:
bekannt
ist. Als Barwert-Formel der Zinseszinsrechung ergibt sich:
(5)¶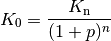
Die Größe 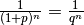 wird auch Abzinsungsfaktor
genannt, die Berechnung des Barwerts als Diskontieren bezeichnet. Diese Methode
kann beispielsweise verwendet werden, um monatliche Ratenzahlungen mit einer
einmaligen Zahlung zu vergleichen.
wird auch Abzinsungsfaktor
genannt, die Berechnung des Barwerts als Diskontieren bezeichnet. Diese Methode
kann beispielsweise verwendet werden, um monatliche Ratenzahlungen mit einer
einmaligen Zahlung zu vergleichen.
Ist in der obigen Gleichung der Zinssatz 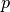 oder die Laufzeit
oder die Laufzeit 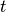 gesucht, während alle anderen Größen gegeben sind, so kann die Gleichung
entsprechend aufgelöst werden:
gesucht, während alle anderen Größen gegeben sind, so kann die Gleichung
entsprechend aufgelöst werden:
Kennt man das Anfangskapital
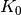 , das Endkapital
, das Endkapital 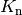 sowie Anzahl
sowie Anzahl  an Zinsperioden, so gilt für den zugehörigen Zinssatz
an Zinsperioden, so gilt für den zugehörigen Zinssatz
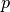 :
:![(1+p)^n = \frac{K_{\mathrm{n}}}{K_0} \quad \Leftrightarrow \quad p =
\sqrt[n]{\frac{K_{\mathrm{n}}}{K_0}}-1](../_images/math/61a483de38e9d5642c477b9fa7db8e4f0180e6ab.png)
Kennt man das Anfangskapital
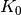 , das Endkapital
, das Endkapital 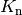 sowie den Zinssatz
sowie den Zinssatz 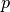 , so gilt mit den Rechenregeln für
Logarithmen für die zugehörige Anzahl
, so gilt mit den Rechenregeln für
Logarithmen für die zugehörige Anzahl
 an Zinsperioden:
an Zinsperioden: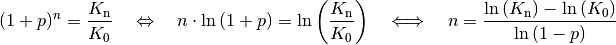
So kann beispielsweise mittels der letzten Formel berechnet werden, dass sich
ein Kapital 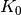 mit einem beliebigen Anfangswert bei einem Zinssatz von
mit einem beliebigen Anfangswert bei einem Zinssatz von
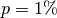 innerhalb von rund
innerhalb von rund ![\unit[70]{Jahren}](../_images/math/b1b0e4b992c843a36dd2129a3c4af23e0193841f.png) verdoppelt. Bei einem
Zinssatz von
verdoppelt. Bei einem
Zinssatz von 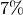 verdoppelt sich das Kapital in rund
verdoppelt sich das Kapital in rund
![\unit[10]{Jahren}](../_images/math/bb189ad135d2827795aa10d959fb5ffbd8d54081.png) , bei einem Zinssatz von
, bei einem Zinssatz von 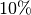 in nur rund
in nur rund
![\unit[7]{Jahren}](../_images/math/82c14f8a8eac86ee87a464c6fa3bcb32eeba5c46.png) . Dies gilt gleichermaßen für Vermögen wie für Schulden:
Zinseszinsen wachsen exponentiell!
. Dies gilt gleichermaßen für Vermögen wie für Schulden:
Zinseszinsen wachsen exponentiell!
