Exkurs: Teilbarkeit und Primzahlen¶
Lässt sich eine natürliche Zahl  ohne Rest durch eine natürliche
Zahl
ohne Rest durch eine natürliche
Zahl  teilen, so nennt man
teilen, so nennt man  ein Vielfaches von
ein Vielfaches von  oder
oder
 einen Teiler von
einen Teiler von  . Bisweilen schreibt man anstelle von
„
. Bisweilen schreibt man anstelle von
„ ist Teiler von
ist Teiler von  “ auch in Kurzform
“ auch in Kurzform 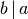 .
.
Jede Zahl  hat die Zahl
hat die Zahl 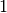 als Teiler, denn es gilt stets
als Teiler, denn es gilt stets
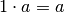 . Ein Teiler, der sowohl zu einer Zahl
. Ein Teiler, der sowohl zu einer Zahl  als auch
zu einer Zahl
als auch
zu einer Zahl  gehört, heißt gemeinsamer Teiler von
gehört, heißt gemeinsamer Teiler von  und
und
 . Haben beide Zahlen keinen gemeinsamen Teiler außer der Zahl
. Haben beide Zahlen keinen gemeinsamen Teiler außer der Zahl
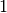 , so nennt man die Zahlen teilerfremd.
, so nennt man die Zahlen teilerfremd.
Die Primfaktorenzerlegung
Hat eine natürliche Zahl 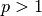 nur zwei Teiler (
nur zwei Teiler (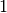 und die Zahl
und die Zahl
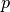 selbst), so heißt sie Primzahl. Die ersten Primzahlen
selbst), so heißt sie Primzahl. Die ersten Primzahlen 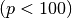 sind:
sind:
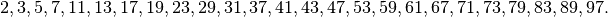
Jede Zahl, die keine Primzahl ist, wird zerlegbar genannt, denn sie lässt sich ohne Rest in mehrere andere Zahlen aufteilen. Hierzu ist folgendes Vorgehen nützlich:
- Zunächst wird geprüft, ob die zu prüfende Zahl
 durch eine
beliebige, betraglich kleinere Primzahl
durch eine
beliebige, betraglich kleinere Primzahl 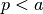 teilbar ist.
teilbar ist. - Wird eine Primzahl
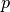 gefunden ist, die ein Teiler von
gefunden ist, die ein Teiler von  ist,
so wird diese Primzahl notiert und
ist,
so wird diese Primzahl notiert und  durch
durch 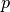 geteilt.
geteilt. - Mit dem Ergebnis der Division wird erneut mit dem 1. Schritt begonnen. Diese Wiederholung wird so lange fortgesetzt, bis keine weitere Aufteilung in Primzahlen möglich ist.
Das obige Verfahren wird auch als „Primfaktorzerlegung“ einer Zahl bezeichnet.
Beispiel:
![17\,640 \; &= 2 \cdot 8820 \\ &= 2 \cdot 2 \cdot 4410 \\ &= 2 \cdot 2 \cdot 2
\cdot 2205 \\ &= 2 \cdot 2 \cdot 2 \cdot 3 \cdot 735 \\ &= 2 \cdot 2 \cdot 2
\cdot 3 \cdot 3 \cdot 245 \\ &= 2 \cdot 2 \cdot 2
\cdot 3 \cdot 3 \cdot 5 \cdot 49 \\ &= 2 \cdot 2 \cdot 2
\cdot 3 \cdot 3 \cdot 5 \cdot 7 \cdot 7 \\[10pt]
\Rightarrow 17\,640 \; &= \quad \; 2^3 \;\;\; \cdot \;\; 3^2 \; \cdot 5^1 \cdot \, 7^2](../_images/math/7692e682f43c3e6185c115aee5a5863740e65f51.png)
Multipliziert man alle Primfaktoren einer Zahl miteinander, wobei einzelne Faktoren mehrfach auftreten dürfen, so erhält man als Ergebnis wiederum die ursprüngliche Zahl. Die gleiche Methode wird auch zur Ermittlung von Primzahlen mittels Computern eingesetzt.[1]
Weitere Teilbarkeitsregeln
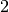 , wenn die letzte Ziffer durch
, wenn die letzte Ziffer durch 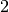 teilbar ist.
teilbar ist.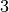 , wenn die Quersumme der Zahl durch
, wenn die Quersumme der Zahl durch 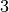 teilbar ist.
teilbar ist.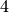 , wenn die aus den beiden letzten Ziffern bestehende Zahl durch 4
teilbar ist.
, wenn die aus den beiden letzten Ziffern bestehende Zahl durch 4
teilbar ist.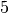 , wenn die letzte Ziffer gleich
, wenn die letzte Ziffer gleich 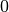 oder
oder 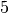 ist.
ist.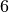 , wenn die letzte Ziffer durch
, wenn die letzte Ziffer durch 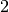 und die Quersumme der Zahl
durch
und die Quersumme der Zahl
durch 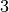 teilbar ist.
teilbar ist.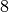 , wenn die aus den drei letzten Ziffern bestehende Zahl durch
, wenn die aus den drei letzten Ziffern bestehende Zahl durch
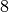 teilbar ist.
teilbar ist.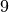 , wenn die Quersumme der Zahl durch
, wenn die Quersumme der Zahl durch 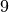 teilbar ist.
teilbar ist.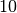 , wenn ihre letzte Ziffer gleich
, wenn ihre letzte Ziffer gleich 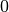 ist.
ist.
Die Quersumme bezeichnet dabei die Summe der Ziffern einer Zahl. Beispielsweise
ist die Quersumme der Zahl  ; somit ist nach der
obigen Regel
; somit ist nach der
obigen Regel 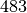 durch
durch 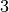 teilbar. Für die Zahl
teilbar. Für die Zahl 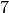 existiert keine triviale Teilbarkeitsregel.
existiert keine triviale Teilbarkeitsregel.
Anmerkungen:
| [1] | Der als „Sieb des Eratosthenes“ bekannte Algorithmus prüft dabei gemäß der obigen Methode für beliebig große natürliche Zahlen, ob diese bereits eine der bereits bekannten Primzahlen als Faktor enthalten. Ist dies der Fall, so wird die Zahl (und ihre Vielfachen) als Nicht-Primzahl markiert und die Prüfung mit der nächsten Zahl fortgesetzt. Enthält eine Zahl keine kleinere Primzahl als Faktor, so stellt sie eine Primzahl dar und wird in die Liste der bekannten Primzahlen aufgenommen. |
| [2] | Der Beweis hierfür ist beispielsweise in [Bittner1979] auf Seite 33 ff. aufgeführt. |
