Beschreibende Statistik¶
In der beschreibenden Statistik geht es um die Erfassung, Auswertung und Darstellung von experimentell oder empirisch gewonnenen Daten. Dabei werden eÂndliche Mengen an Objekten hinsichtlich bestimmter Eigenschaften untersucht. Dabei werden allgemein folgende Schritt durchlaufen:
- Zunächst müssen in der beschreibenden Statistik alle für die Analyse relevanten Daten vollständig erhoben werden.
- Das bei der Daten-Erhebung gewonnene, oftmals sehr umfangreiche Datenmaterial muss als nächstes in eine übersichtliche Form gebracht werden, üblicherweise in eine Tabelle oder eine Graphik.
- Anschließend kann mit der Analyse der Daten begonnen werden. Hierbei lassen sich die Daten beispielsweise mittels wichtiger Kennzahlen wie Mittelwert und Streuungsmaß charakterisieren, ebenso können beispielsweise zeitliche Trends oder Abhängigkeiten zwischen mehreren Größen untersucht werden.
- Zuletzt können die Ergebnisse der Analyse interpretiert werden.
Merkmale, Merkmalsträger und Grundgesamtheit
Als (Untersuchungs-)Merkmal wird die interessierende statistische Information bezeichnet. Ein einzelnes Objekt, das dieses Merkmal besitzt, nennt man Merkmalsträger. Die möglichen Werte, die ein Merkmal annehmen kann, heißen Merkmalswerte oder Ausprägungen dieses Merkmals.[1]
Die Menge an Objekten 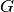 , die hinsichtlich einem oder mehrerer zu
untersuchender Merkmale gleichwertig sind, wird als „Grundgesamtheit“ oder
„Population“ bezeichnet. Bei der Festlegung der Grundgesamtheit werden müssen
klare Abgrenzungen getroffen werden, beispielsweise müssen räumliche oder
zeitliche Einschränkung vorliegen; die Mitglieder der Grundgesamtheit müssen
somit nicht nur Träger des Untersuchungsmerkmals sein, sondern auch
übereinstimmende Abgrenzungsmerkmale besitzen.
, die hinsichtlich einem oder mehrerer zu
untersuchender Merkmale gleichwertig sind, wird als „Grundgesamtheit“ oder
„Population“ bezeichnet. Bei der Festlegung der Grundgesamtheit werden müssen
klare Abgrenzungen getroffen werden, beispielsweise müssen räumliche oder
zeitliche Einschränkung vorliegen; die Mitglieder der Grundgesamtheit müssen
somit nicht nur Träger des Untersuchungsmerkmals sein, sondern auch
übereinstimmende Abgrenzungsmerkmale besitzen.
Beispiel:
- Bei einem naturwissenschaftlichen Experiment sind die einzelnen Messungen die Merkmalsträger, die ihrerseits Messdaten als Merkmale enthalten.
- Bei einer Inventur werden zu einem bestimmten Zeitpunkt alle Objekte eines räumlich abgegrenzten Bereichs beispielsweise hinsichtlich ihrer Funktionsfähigkeit als Merkmal untersucht.
Die Mächtigkeit 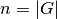 der Grundgesamtheit ist gleich der Anzahl ihrer
Objekte. In Tabellen werden die einzelnen zu untersuchenden Merkmale häufig
einem Buchstaben
der Grundgesamtheit ist gleich der Anzahl ihrer
Objekte. In Tabellen werden die einzelnen zu untersuchenden Merkmale häufig
einem Buchstaben 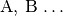 zugeordnet, die einzelnen zu
einem jeweiligen Merkmalsträger gehörenden Merkmalswerte werden zeilenweise
durchnummeriert und in der jeweiligen Spalte eingetragen.
zugeordnet, die einzelnen zu
einem jeweiligen Merkmalsträger gehörenden Merkmalswerte werden zeilenweise
durchnummeriert und in der jeweiligen Spalte eingetragen.
Meist ist bei einer Daten-Erhebung nicht möglich, alle Mitglieder der Grundgesamtheit zu untersuchen („Vollerhebung“). In diesem Fall muss sich die Statistik mit einer kleineren, möglichst repräsentativen Stichprobe auskommen und von dieser auf die Gesamtheit schließen.
Qualitative und quantitative Merkmale
Merkmale können allgemein in zwei Gruppen unterteilt werden:
- Qualitative Merkmale lassen sich nur verbal beschreiben, es können nur Namen oder Klassenbezeichnungen als Werte vorkommen.
Handelt es sich bei den Merkmalswerten um Namen, so spricht man auch von artmäßigen Merkmalen. Beispiele für derartige Merkmale sind Familiennamen, Geschlecht, Farbbezeichnungen, usw.
Handelt es sich bei den Merkmalswerten um Klassenbezeichnungen, so spricht man auch von intensitätsmäßig abgestuften Merkmalen. Ein Beispiele hierfür sind Schulnoten („sehr gut“, „gut“, usw.).
Qualitative Merkmale lassen sich zudem in „häufbare“ und „nicht häufbare“ Merkmale unterscheiden. Ein qualitatives Merkmal ist häufbar, wenn ein Merkmalsträger mehrere Merkmalswerte gleichzeitig aufweisen kann; beispielsweise kann eine Person gegebenenfalls mehrere Berufsausbildungen absolviert haben. Ein qualitatives Merkmal ist nicht häufbar, wenn ein Merkmalsträger nur genau einen Merkmalswert aufweisen kann; beispielsweise hat jede Person genau eine Augenfarbe.
Quantitative Merkmale können als Vielfaches einer Einheit ausgedrückt werden, beispielsweise Zeitdauer, Energiebedarf, usw.
Können bei einem quantitativen Merkmal nur ganzzahlige Werte auftreten, so spricht man von einem diskreten Merkmal. Ein Beispiel hierfür sind Stückzahlen.
Können bei einem quantitativen Merkmal beliebige Werte auftreten, so spricht man von einem stetigen oder kontinuierlichen Merkmal. Beispiele hierfür sind Zeitdauern, Längenangaben, usw.
Um eine Vielzahl unterschiedlicher quantitativer Messwerte abzubilden, können
diese in einzelne Intervalle zusammengefasst werden. Anstelle (sehr) viele
Einzelergebnisse aufzulisten, genügt es damit, die Anzahl an Werten in den
einzelnen Intervallen anzugeben. Üblicherweise werden zwischen 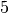 und
und
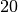 einzelne Intervallen mit jeweils gleich großen Intervallen und
eindeutig zuzuordnenden Intervallgrenzen gewählt. Durch diese Methode gehen zwar
einerseits die statistischen Informationen der Einzelmessungen teilweise
verloren, andererseits werden dafür die Ergebnisse „komprimiert“ und somit
übersichtlicher.
einzelne Intervallen mit jeweils gleich großen Intervallen und
eindeutig zuzuordnenden Intervallgrenzen gewählt. Durch diese Methode gehen zwar
einerseits die statistischen Informationen der Einzelmessungen teilweise
verloren, andererseits werden dafür die Ergebnisse „komprimiert“ und somit
übersichtlicher.
Statistische Mess-Skalen¶
Mittels einer Mess-Skala können die möglichen Merkmalswerte nach bestimmten Ordnungsprinzipien darstellt werden. Für qualitative Merkmale werden Nominal- oder Ordinalskalen verwendet, für quantitative Merkmale kommen oftmals Intervall- oder Verhältnisskalen zum Einsatz. Im folgenden Abschnitt werden diese Skalen näher beschrieben.
Nominalskala
Eine Nominalskala hat die möglichen Namen eines quantitativen Merkmals als Skalenwerte. Diese werden gleichberechtigt nebeneinander angeordnet. Die einzelnen Namen können zur Unterscheidung von artmäßigen Merkmalen genutzt werden, entsprechen jedoch keiner Rangordnung. Nehmen die einzelnen Namen zu viel Platz ein, so können ihnen auch Abkürzungen oder Nummern als Schlüsselwerte zugewiesen werden.
Ordinalskala
Eine Ordinalskala hat die Klassenbezeichnungen eines quantitativen Merkmals als Skalenwerte. Im Gegensatz zu einer Nominalskala sind die einzelnen Klassenbezeichnungen nicht gleichwertig, sondern entsprechen einer Rangordnung in auf- oder absteigender Folge.
Intervall- und Verhältnisskala
Bei diesen beiden Skalentypen handelt es sich um metrische Skalen, vergleichbar mit einem Meterstab. Als Skalenwerte werden Vielfache einer Grundeinheit abgetragen.
Eine metrische Skala heißt Intervallskala, wenn der Nullpunkt willkürlich
gewählt ist; in diesem Fall können zwar Differenzen zwischen zwei Werten
sinnvoll interpretiert werden, Quotienten hingegen nicht; Beispielsweise
entsprechen ![\unit[20]{\degree C}](../_images/math/34ab305b55c39e1662ea5f9300890497ea45c898.png) nicht einer doppelt so hohen Temperatur
wie
nicht einer doppelt so hohen Temperatur
wie ![\unit[10]{\degree C}](../_images/math/b85c04de9f97abaa40215864668c04b9e537fa4e.png) , wenn man vom absoluten Temperaturnullpunkt
, wenn man vom absoluten Temperaturnullpunkt
![T_0 = \unit[-273]{\degree C}](../_images/math/46d991eff5b52a7e7ba449ca296ccfbe54847031.png) ausgeht.
ausgeht.
Ist der Nullpunkt einer Skala eindeutig festgelegt, so spricht man von einer Verhältnisskala. In diesem Fall sind auch Quotienten von einzelnen Werten sinnvoll interpretierbar. Beispiele hierfür sind Gewichtsangaben, Geldmengen, Stückzahlen, absolute Temperaturangaben usw.
Graphische Darstellungen statistischer Daten¶
Bisweilen ist es praktisch, statistische Informationen als Diagramme graphisch darzustellen; diese müssen einerseits eindeutig beschriftet sein und sollten andererseits möglichst übersichtlich gestaltet werden.
- Bei einem Histogramm werden auf der waagrechten Achse die einzelnen Intervall- oder Klassengrenzen abgetragen. Über den einzelnen Intervallen werden Rechtecke gezeichnet, deren Höhe die absoluten oder relativen Häufigkeiten des jeweiligen Intervalls oder der jeweiligen Klasse darstellen.
- Todo: Tortendiagramm, Liniendiagramm, Boxplot usw.
Umgang mit ungenauen Messwerten¶
Als Messfehler werden Differenzen zwischen gemessenen Werten und den unbekannten wahren Werten der jeweiligen Messgrößen bezeichnet. Sie lassen sich grundsätzlich in zwei Arten unterteilen – in systematische und statistische (zufällige) Fehler.
Systematische Fehler
Systematische Fehler entstehen durch mangelhafte Messverfahren, beispielsweise durch defekte Messgeräte, falsche Eichungen, oder Vernachlässigung von störenden Einflussgrößen. Je nach Fehler weichen die gemessenen Werte entweder nach oben oder nach unten von den tatsächlichen Werten ab.
Systematische Fehler werden „reproduzierbar“ genannt, denn bei erneuten Messvorgängen treten sie unter gleichen Bedingungen erneut auf. Wird der Fehler gefunden, so kann er berücksichtigt und eventuell korrigiert werden.
Statistische Fehler
Statistische Fehler entstehen zufällig, beispielsweise durch Schwankungen in Messgeräten oder durch ein ungenaues Ablesen von analogen Messgeräten. Die Abweichungen der gemessenen Werte können unabhängig vom Fehler sowohl nach oben als auch nach unten von den tatsächlichen Werten abweichen.
Statistische Fehler können nicht nie komplett vermieden werden. Die Messgenauigkeit kann jedoch erhöht werden, indem mehrere Messungen oder Stichprobentests unter gleichen Bedingungen durchgeführt werden.
Die Summe aller nicht erfassbaren systematischen und zufälligen Fehler ergibt den Größtfehler einer Datenaufnahme beziehungsweise Messung.
Setzt sich ein Ergebnis rechnerisch aus mehreren gemessenen Größen zusammen, so hat auch dieses einen Fehler, der sich aus den Fehlern der Einzelgrößen ergibt. Dabei gelten für verschiedene Rechenoperationen verschiedene Regeln:
Bei Summen und Differenzen (also
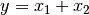 oder
oder 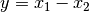 ) werden die Absolutfehler der Einzelgrößen quadriert und addiert;
die Quadratwurzel aus diesem Wert liefert schließlich den Fehler der
Ergebnisgröße:
) werden die Absolutfehler der Einzelgrößen quadriert und addiert;
die Quadratwurzel aus diesem Wert liefert schließlich den Fehler der
Ergebnisgröße: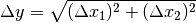
Bei Produkten und Quotienten (also
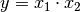 oder
oder 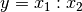 ) werden die relativen Fehler unter der Wurzel quadratisch
addiert:
) werden die relativen Fehler unter der Wurzel quadratisch
addiert: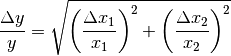
Bei Potenzen und Wurzeln (also
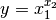 ) wird der relative
Fehler von y bestimmt durch
) wird der relative
Fehler von y bestimmt durch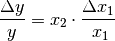
Dies gilt auch für
 (Wurzeln).
(Wurzeln).
Mittelwerte und Streuungsmaße¶
Nicht nur bei der Fehlerrechnung hat man bei statistischen Analysen als Ziel, die Gesamtheit aller Merkmalswerte mit einigen charakteristischen Größen zusammenzufassen; diese sollten beispielsweise einen durchschnittlichen Wert sowie die Streuung der Merkmalswerte um diesen Durchschnittswert beziffern.
Mittelwerte¶
Mit „Mittelwert“ bezeichnet man umgangssprachlich meist das so genannte arithmetische Mittel; bisweilen sind allerdings auch andere Durchschnittswerte wie Median- oder Modalwerte besser zur Beschreibung einer Häufigkeitsverteilung geeignet.
Arithmetisches Mittel¶
Hat man eine Folge von  gemessenen Elementarereignissen vorliegen, so
schwanken die Messwert
gemessenen Elementarereignissen vorliegen, so
schwanken die Messwert  der Ereignisse um den Mittelwert
der Ereignisse um den Mittelwert
 , der folgendermaßen definiert ist:
, der folgendermaßen definiert ist:
(1)¶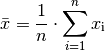
Der Mittelwert 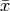 wird auch als „arithmetisches Mittel“ der
Zahlenfolge bezeichnet. Die Abweichungen der einzelnen Ereignisse
wird auch als „arithmetisches Mittel“ der
Zahlenfolge bezeichnet. Die Abweichungen der einzelnen Ereignisse
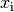 von diesem Mittelwert betragen:
von diesem Mittelwert betragen:
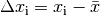
Der Mittelwert ist zwar anschaulich und einfach zu berechnen, allerdings empfindlich gegen unerwartet hohe beziehungsweise niedrige Merkmalswerte, so genannte „Ausreißer“.
Gewichtetes arithmetisches Mittel
Das gewichtete (arithmetische) Mittel ist arithmetische Mittel einer Häufigkeitsverteilung. Man verwendet diesen Wert, wenn die Merkmalswerte mit unterschiedlichen Häufigkeiten gewichtet sind.
Um das gewichtete Mittel zu berechnen, multipliziert man zunächst die
unterschiedlichen Merkmalswerte 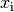 mit ihrer jeweiligen
Häufigkeit
mit ihrer jeweiligen
Häufigkeit 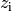 ; anschließend addiert man
alle resultierenden Produkt-Werte und teilt das Ergebnis durch die Anzahl
; anschließend addiert man
alle resultierenden Produkt-Werte und teilt das Ergebnis durch die Anzahl
 aller Messungen:
aller Messungen:
(2)¶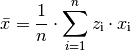
Hat man anstelle der (absoluten) Häufigkeiten 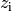 die
relativen Häufigkeiten
die
relativen Häufigkeiten 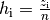 gegeben, so genügt es, diese mit den jeweiligen Merkmalswerten
gegeben, so genügt es, diese mit den jeweiligen Merkmalswerten 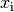 zu multiplizieren und die resultierenden Produkte zu addieren:
zu multiplizieren und die resultierenden Produkte zu addieren:
(3)¶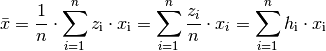
Beispiel:
Bei der Statistischen Erhebung „Mikrozensus 2015“ hat sich die in der folgenden Tabelle dargestellte Häufigkeitsverteilung für die Anzahl an Kindern (unter
 Jahren) in Haushalten und Familien ergeben (Quelle: Destatis).
Wie viele Kinder gibt es durchschnittlich je Familie?
Jahren) in Haushalten und Familien ergeben (Quelle: Destatis).
Wie viele Kinder gibt es durchschnittlich je Familie?Kinder je Haushalt Anzahl  an Familien in
an Familien in 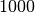
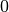
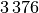
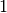
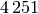
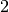
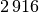
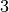
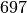
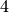
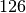
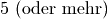
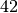
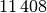
Da die unterschiedlichen Kinder-Anzahlen unterschiedlich gewichtet sind, muss zur Bestimmung des Durchschnittwerts mit der Formel für das gewichtete arithmetische Mittel gerechnet werden:
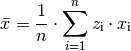
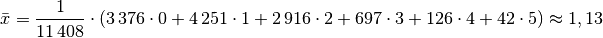
Je Familie gibt es in Deutschland somit durchschnittlich (nur) rund
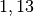 Kinder unter
Kinder unter 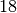 Jahren.
Jahren.
Geometrisches Mittel¶
Sind die Merkmalswerte relative Änderungen, wie es beispielsweise bei
Wachstumraten oder Leistungssteigerungen der Fall ist, so wird bevorzugt das
geometrische Mittel 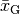 als Durchschnittswert
verwendet. Sie die einzelnen Merkmalswerte
als Durchschnittswert
verwendet. Sie die einzelnen Merkmalswerte
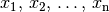 allesamt positiv, so kann das
geometrische Mittel
allesamt positiv, so kann das
geometrische Mittel 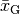 folgendermaßen berechnet
werden:
folgendermaßen berechnet
werden:
(4)¶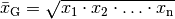
Beispiel:
In einer bestimmten Bakterien-Kultur erhöhte sich in drei Tagen die Zahl der Bakterien pro Einheit von
 auf
auf 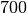 . Gefragt ist nach der
durchschnittlichen prozentualen Zunahme (je Tag).
. Gefragt ist nach der
durchschnittlichen prozentualen Zunahme (je Tag).Die durchschnittliche Zunahme soll mit
 bezeichnet werden. Für die Zahl
der Bakterien nach dem ersten Tag ergibt sich damit:
bezeichnet werden. Für die Zahl
der Bakterien nach dem ersten Tag ergibt sich damit: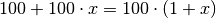
Für den zweiten Tag ist der Wert
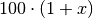 der neue
Ausgangswert. Stellt man die obige Gleichung für den zweiten Tag auf, so muss
also lediglich
der neue
Ausgangswert. Stellt man die obige Gleichung für den zweiten Tag auf, so muss
also lediglich 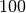 durch
durch 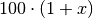 ersetzt werden. Man
erhält als Anzahl der Bakterien nach dem zweiten Tag:
ersetzt werden. Man
erhält als Anzahl der Bakterien nach dem zweiten Tag: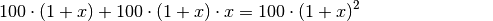
Hierbei wurde zunächst der gemeinsame Faktor
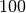 ausgeklammert und
anschließend der resultierende Term zusammengefasst:
ausgeklammert und
anschließend der resultierende Term zusammengefasst: ![100 \cdot [(1+x) +
(1+x)\cdot x] = 100 \cdot (1 +x +x + x^2)](../_images/math/a7e82682c1570cb0b0009c657046d3c6fe333851.png) . Der Term in der Klammer kann als
. Der Term in der Klammer kann als
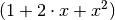 geschrieben werden und entspricht somit der
binomischen Formel
geschrieben werden und entspricht somit der
binomischen Formel 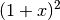 .
.Für den dritten Tag erhält man mit
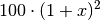 als neuem
Ausgangswert:
als neuem
Ausgangswert: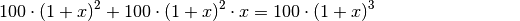
Hierbei wurde zunächst wiederum der gemeinsame Faktor
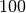 ausgeklammert und anschließend der resultierende Term in der Klammer
ausmultipliziert. Man erhält so
ausgeklammert und anschließend der resultierende Term in der Klammer
ausmultipliziert. Man erhält so ![100 \cdot \left[ (1 + 2 \cdot x + x^2)
+(x+ 2\cdot x^2 + x^3) \right]](../_images/math/8a49349f5951d332a8568e9c768e5865fa5d5b53.png) , was sich zu
, was sich zu 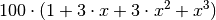 zusammenfassen lässt; dies entspricht wiederum der
binomischen Formel
zusammenfassen lässt; dies entspricht wiederum der
binomischen Formel 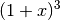 .
.Der Wert des letzten Ausdrucks soll gemäß der Angabe gleich
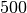 sein;
es muss also gelten:
sein;
es muss also gelten:![100 \cdot (1 + x)^3 &= 700 \\
\Rightarrow (1 + x)^3 &= \frac{700}{100} \\
(1 + x) &= \sqrt[3]{\frac{700}{100}} \\
x &= \sqrt[3]{\frac{700}{100}} - 1 \approx 0,91 \\](../_images/math/110cf3da12e375c7264f6af75d2251ad88eaca58.png)
Die durchschnittliche Wachstumsrate beträgt somit rund
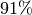 .
.
Es kann gezeigt werden, dass das geometrische Mittel einer Merkmals-Reihe der
Länge  allgemein nach diesem Prinzip berechnet werden kann:
allgemein nach diesem Prinzip berechnet werden kann:
(5)¶![\bar{x}_{\mathrm{G}} = \sqrt[n]{\frac{\text{Endwert}}{\text{Anfangswert}}}](../_images/math/811e741d296ab3ed7afbed108f19ca3a5fc22d8b.png)
Hat ein Merkmal zu Beginn der Messungen einen Wert 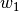 , so erhält man
allgemein bei einem gleichmäßigen Wachstum über
, so erhält man
allgemein bei einem gleichmäßigen Wachstum über  Zeitschritte den neuen
Wert
Zeitschritte den neuen
Wert 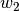 gemäß folgender Formel:
gemäß folgender Formel:
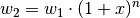
Hierbei bezeichnet  wiederum die Zuwachsrate je Zeitschritt.
wiederum die Zuwachsrate je Zeitschritt.
Beispiel:
Der Wert einer Aktie, deren Kaufpreis
![\unit[50]{Eur}](../_images/math/8c6989f963b9f48c8c42ecb09dfd2bd5bbd91513.png) betrug, stieg im
ersten Jahr auf
betrug, stieg im
ersten Jahr auf ![\unit[70]{Eur}](../_images/math/7abd8306c8a6b684653e5283ccfe91d19d45de51.png) , fiel jedoch im zweiten Jahr auf
, fiel jedoch im zweiten Jahr auf
![\unit[40]{Eur}](../_images/math/9df7c82bc39eaa32a175fb13158b471421ef9970.png) . Wie groß ist die mittlere Wachstumsrate?
. Wie groß ist die mittlere Wachstumsrate?Für die relative Wachstumsrate
 im ersten Jahr gilt:
im ersten Jahr gilt: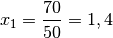
Für die relative Wachstumsrate
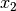 im zweiten Jahr gilt dafür:
im zweiten Jahr gilt dafür: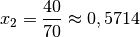
Für das geometrische Mittel
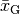 zwischen diesen
beiden Werten beträgt:
zwischen diesen
beiden Werten beträgt: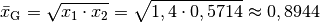
Der Wert des geometrischen Mittels ist in diesem Fall kleiner als
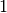 ,
was eine Verringerung des ursprünglichen Werts bedeutet. Die jährliche
„Wachstumsrate“ beträgt also
,
was eine Verringerung des ursprünglichen Werts bedeutet. Die jährliche
„Wachstumsrate“ beträgt also 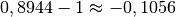 , also rund
, also rund
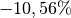 .
.
Wie man an den beiden Beispielen erkennen kann, wird das geometrische Mittel vor allem zur Bestimmung des Durchschnittswertes von Verhältniszahlen genutzt, wobei die Veränderungen meist in jeweils gleichen zeitlichen Abschnitten angegeben sind.
Harmonisches Mittel¶
Das harmonische Mittel wird dann verwendet, wenn die Merkmalswerte in Form von Quotienten vorliegen, wie dies beispielsweise bei der Berechnung von Durchschnitts-Geschwindigkeiten oder Bevölkerungsdichten der Fall ist.
Die einzelnen Merkmalswerte 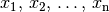 müssen
allesamt positiv oder allesamt negativ sein; das harmonische Mittel
müssen
allesamt positiv oder allesamt negativ sein; das harmonische Mittel
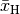 lässt sich dann schrittweise folgendermaßen
berechnen:
lässt sich dann schrittweise folgendermaßen
berechnen:
- Man dividiert die einzelnen Merkmalswerte
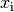 durch ihre
jeweiligen (absoluten) Häufigkeiten
durch ihre
jeweiligen (absoluten) Häufigkeiten 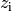 und bildet dabei
jeweils die Kehrwerte der Ergebnisse.
und bildet dabei
jeweils die Kehrwerte der Ergebnisse. - Alle so erhaltenen Kehrwerte werden aufsummiert und der Kehrwert dieser Summe gebildet.
- Der Kehrwert dieser Summe wird mit der Anzahl
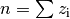 multipliziert.
multipliziert.
Die Formel zur Berechnung des harmonischen Mittels lautet also:
(6)¶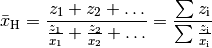
Beispiele:
Ein Fahrradfahrer fährt eine
![\unit[5]{km}](../_images/math/bab864b9acc0dfba261d6509846d5cbf26ad40fb.png) lange Strecke zunächst mit
lange Strecke zunächst mit
![\unit[10]{km/h}](../_images/math/34b3d661deaf3398b5a42a19a98b34101370b2ab.png) bergauf, anschließend mit
bergauf, anschließend mit ![\unit[30]{km/h}](../_images/math/2f233deeb1d966b9dc7ea734e91968886169e14d.png) bergab. Wie groß ist die Durchschnittsgeschwindigkeit des Fahrers?
bergab. Wie groß ist die Durchschnittsgeschwindigkeit des Fahrers?Die beiden auftretenden Merkmalswerte sind
![x_1 = \unit[10]{km/h}](../_images/math/db299ef3318aa2f9117041ccc7e09ae12c2a92d1.png) und
und
![x_2 = \unit[30]{km/h}](../_images/math/a0532240807bd80786d7375aa9408c43612b071a.png) ; sie treten mit den Häufigkeiten
; sie treten mit den Häufigkeiten ![z_1 =
z_2 = \unit[5]{km}](../_images/math/6292f69f158d5e597b442233fb6d6ea335cd4e8d.png) auf. Da es sich bei den Merkmalswerten um Quotienten
handelt, muss zur Berechnung des Durchschnittswertes auf das harmonische
Mittel zurückgegriffen werden:
auf. Da es sich bei den Merkmalswerten um Quotienten
handelt, muss zur Berechnung des Durchschnittswertes auf das harmonische
Mittel zurückgegriffen werden:![\bar{x}_{\mathrm{H}} = \frac{z_1 + z_2}{\frac{z_1}{x_1} + \frac{z_2}{x_2}}
= \frac{\unit[(5 + 5)]{km}}{\frac{\unit[5]{km}}{\unit[10]{\frac{km}{h}}} +
\frac{\unit[5]{km}}{\unit[30]{\frac{km}{h}}} } = \unit[15]{km/h}](../_images/math/633614cf490f66c917b1221f8414f3202c7d9741.png)
Die geringe Geschwindigkeit fällt stärker ins Gewicht, da der Fahrer bergauf mehr Zeit benötigt als bergab.
Die Bevölkerungszahlen der Bundesländer Bayern und Baden-Württemberg sind in der folgenden Tabelle dargestellt (Quelle: Wikipedia, Stand: Dezember 2016). Wie viel Einwohner je
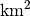 gibt es durchschnittlich in diesen
beiden Ländern?
gibt es durchschnittlich in diesen
beiden Ländern?Land Fläche in 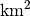
Einwohner Einwohner je 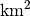
Baden-Württemberg 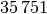
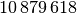
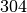
Bayern 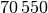
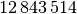
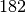
Sind auch die absoluten Einwohnerzahlen bekannt, so kann man diese aufsummieren und das Resultat durch die Gesamtfläche dividieren. Kennt man hingegen nur die Einwohnerzahlen je
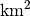 , so kann man zur
Berechnung des Durchschnittswerts die Formel für das harmonische Mittel
verwenden:
, so kann man zur
Berechnung des Durchschnittswerts die Formel für das harmonische Mittel
verwenden:![\bar{x}_{\mathrm{H}} = \frac{z_1 + z_2}{\frac{z_1}{x_1} + \frac{z_2}{x_2}}
= \frac{\unit[(35\,751 + 70\,550)]{km^2}}{\frac{\unit[35\,751]{km^2}}{\unit[304]{\frac{1}{km^2}}} +
\frac{\unit[70\,550]{km^2}}{\unit[182]{\frac{1}{km^2}}} } \approx \unit[210,4]{\frac{1}{km^2}}](../_images/math/3ceaa4b3cc076cf78d348e5d4a5d38e872b0df4e.png)
Die durchschnittliche Bevölkerungsdichte in diesen beiden Bundesländern liegt somit unterhalb des Durchschnittwerts für ganz Deutschland (laut obiger Quelle rund
![\unit[230]{\frac{1}{km^2}}](../_images/math/6a21abae0737d01bd6c7f98680bf204bee107286.png) , Stand: Dezember 2016).
, Stand: Dezember 2016).
Wie man an den Beispielen erkennen kann, wird das harmonische Mittel dann verwendet, wenn die Gewichtungen in der gleichen Einheit vorliegen wie der Zähler oder der Nenner des Merkmals.
Median¶
Wesentlich unempfindlicher gegenüber Ausreißern ist der so genannte Medianwert. Sortiert man alle Merkmalswerte in aufsteigender Reihenfolge, so entspricht der Medianwert genau dem Wert, der sich in der Mitte dieser Liste befindet.
Bei einer Liste mit einer ungeradzahligen Anzahl von
 Elementarereignissen entspricht der mittlere Platz der Position
Elementarereignissen entspricht der mittlere Platz der Position
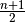 in der Liste; der Medianwert entspricht somit dem Wert
in der Liste; der Medianwert entspricht somit dem Wert
![x_{\mathrm{\left[\frac{n+1}{2}\right]}}^{\phantom{X}}](../_images/math/9e9c2043b89ba9bd16882061802c19ee0ccdbb31.png) der Liste:
der Liste:![Me = x_{\mathrm{\left[\frac{n+1}{2}\right]}}](../_images/math/bf749987d06b48f8ab2f1325482061b5fd05fa74.png)
Bei einer Liste mit einer geradzahligen Anzahl von
 Elementarereignissen entspricht der Median dem Durchschnitt aus den beiden
mittig gelegenen Werten:
Elementarereignissen entspricht der Median dem Durchschnitt aus den beiden
mittig gelegenen Werten:![Me = \frac{1}{2} \cdot \big( x_{\mathrm{\left[\frac{n+1}{2}\right]}} +
x_{\mathrm{\left[\frac{n+1}{2}\right]}} \big)](../_images/math/4623a91c25b918742c3ba161571363dd38c0e142.png)
Der Median ist somit ebenfalls schnell und einfach zu bestimmen.
Modalwert¶
Der Modalwert, bisweilen auch „Modus“ genannt, gibt den Wert einer Messreihe an, der am häufigsten beobachtet wurde. Üblicherweise wird der Modalwert nur dann verwendet, wenn sich die damit verbundene Häufigkeit deutlich von den restlichen Häufigkeiten unterscheidet; der Modalwert sollte also ein herausragender Wert sein.
Da die restlichen Merkmalswerte unberücksichtigt bleiben, wird der Modalwert von Ausreißern nicht beeinflusst.
Streuungsmaße¶
Zusätzlich zum Mittelwert sollte stets (mindestens) ein Streuungsmaß angegeben werden, das angibt, wie stark die tatsächlichen Merkmalswerte vom Mittelwert abweichen. Beispielsweise sind bei „genauen“ Messungen die Abweichungen nur gering, während sie sich bei „ungenauen“ Messungen über einen größeren Skalenbereich erstrecken.
Spannweite und Quantile
Als Spannweite 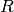 , im Englischen „range“ genannt, bezeichnet man die
Differenz aus dem größten und dem kleinsten beobachteten Merkmalswert:
, im Englischen „range“ genannt, bezeichnet man die
Differenz aus dem größten und dem kleinsten beobachteten Merkmalswert:
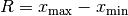
Die Spannweite ist zwar ein einfaches und anschauliches Streuungsmaß, gibt allerdings keine näheren Informationen über die konkrete Verteilung der Merkmalswerte an und ist zudem anfällig gegenüber so genannten „Ausreißern“, also einzelnen ungewöhnlich niedrigen oder hohen Werten.
Besser geeignet sind daher meist so genannte Quantils-Angaben: Hierbei sortiert man zunächst alle Merkmalswerte ihrer Größe nach und untergliedert diese dann in mehrere Teile:
- Bei Quartilen wird die Gesamtheit aller Merkmalswerte in vier gleich große Bereiche unterteilt.
- Bei Dezilen wird die Gesamtheit aller Merkmalswerte in zehn gleich große Bereiche unterteilt.
Die Berechnung der einzelnen Quantile erfolgt in ähnlicher Weise wie die
Berechnung des Median-Werts; beispielsweise gibt das erste
Quartil an, dass 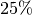 aller Merkmalswerte kleiner und folglich
aller Merkmalswerte kleiner und folglich
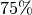 aller Werte größer als der Wert des ersten Quartils sind.[2] Der
Wert des zweiten Quartils gibt entsprechend an, dass
aller Werte größer als der Wert des ersten Quartils sind.[2] Der
Wert des zweiten Quartils gibt entsprechend an, dass 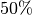 der
Merkmalswerte kleiner beziehungsweise größer als dieser Wert sind; dieser Wert
ist somit mit dem Median-Wert identisch.
der
Merkmalswerte kleiner beziehungsweise größer als dieser Wert sind; dieser Wert
ist somit mit dem Median-Wert identisch.
Standardabweichung
Als Schwankungsbreite wird gewöhnlich die Wurzel aus der mittleren quadratischen
Abweichung vom Mittelwert angegeben. Diese Größe wird Standardabweichung
 genannt:
genannt:
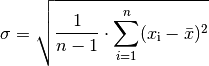
Die Standardabweichung ist, abgesehen von statistischen Schwankungen, unabhängig
von der Anzahl  der Einzelmessungen.
der Einzelmessungen.
… to be continued …
Anmerkungen:
| [1] | Ein Merkmal kann auch als eine Abbildung
Eine derartige Abbildung ist nicht zwingend eindeutig: Ein Merkmalsträger kann mehrere Merkmals-Ausprägungen aufweisen; beispielsweise kann eine Person in mehreren Vereinen aktiv sein, mehrere Sprachen sprechen usw. |
| [2] | Zur Berechnung des ersten Quartilswert prüft man, ob man bei einer
Merkmalsliste der Länge
Ist
|
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

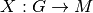 aufgefasst
werden, welche die einzelnen Merkmalsträger
aufgefasst
werden, welche die einzelnen Merkmalsträger 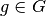 auf Ausprägungen
auf Ausprägungen
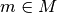 abbildet:
abbildet: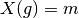
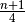 eine
ganzzahlige Zahl erhält. Ist dies der Fall, so gilt für den ersten Quartilswert:
eine
ganzzahlige Zahl erhält. Ist dies der Fall, so gilt für den ersten Quartilswert:![q_1 = x_{\mathrm{ \left[ \frac{n+1}{4} \right] }}](../_images/math/241c85d6aea7f798ba43632688011924cb28a017.png)
![q_1 = x_{\mathrm{ \left[ \frac{n+1}{4} \right] }} + R \cdot \left( x_{\mathrm{
\left[ \frac{n+1}{4} + 1 \right] }} - x_{\mathrm{ \left[ \frac{n+1}{4}
\right] }} \right)](../_images/math/6430430ed6c520495ee96ff052fb80c4e000bd7f.png)