Integralrechnung¶
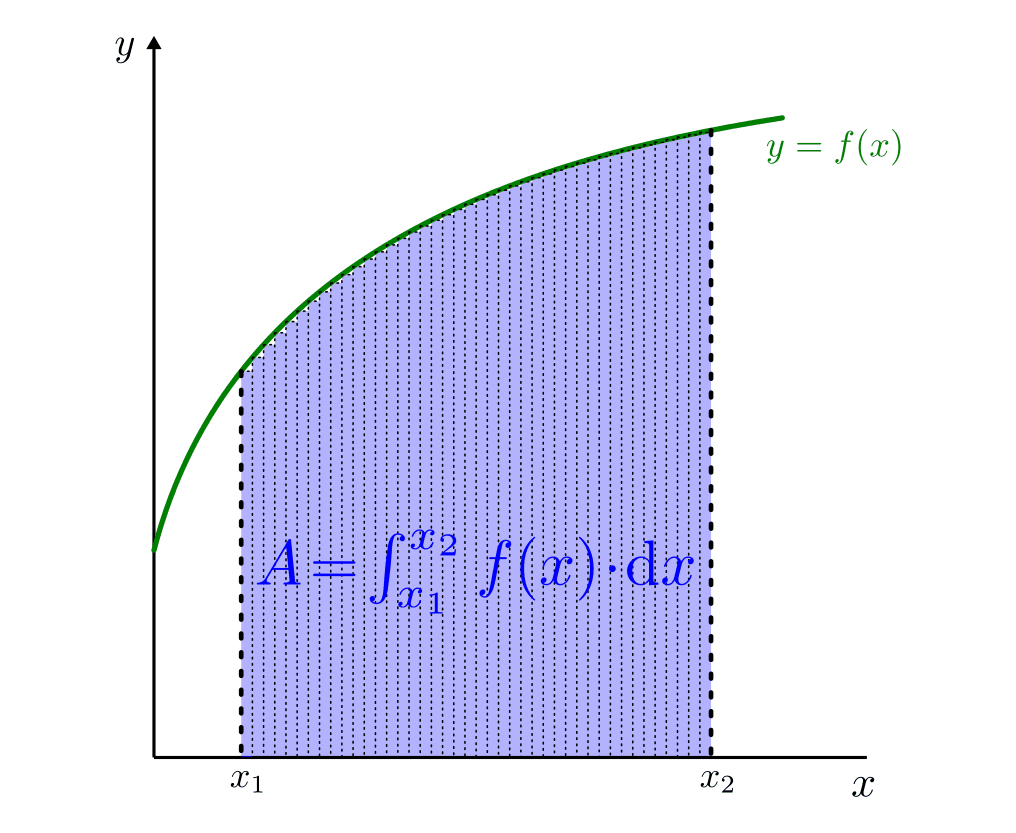
Um Flächen zu bestimmen, die von krummlinigen Funktionsgraphen und der
 -Achse eingeschlossen werden, entwickelte der Mathematiker Bernhard
Riemann die Integralrechnung.
Der Grundgedanke hinter den so genannten „Riemann-Summen“ ist, dass sich jede
derartige Fläche in eine Vielzahl von schmalen Rechtecken zerlegen lässt, wobei
die Grundseiten aller Rechtecke auf der
-Achse eingeschlossen werden, entwickelte der Mathematiker Bernhard
Riemann die Integralrechnung.
Der Grundgedanke hinter den so genannten „Riemann-Summen“ ist, dass sich jede
derartige Fläche in eine Vielzahl von schmalen Rechtecken zerlegen lässt, wobei
die Grundseiten aller Rechtecke auf der  -Achse liegen und die Höhen der
Rechtecke durch die Funktionswerte an den jeweiligen Stellen gegeben sind. Die
Summe der Flächen aller Rechtecke ergibt dann die Fläche zwischen dem
Funktionsgraph und der
-Achse liegen und die Höhen der
Rechtecke durch die Funktionswerte an den jeweiligen Stellen gegeben sind. Die
Summe der Flächen aller Rechtecke ergibt dann die Fläche zwischen dem
Funktionsgraph und der  -Achse.
-Achse.
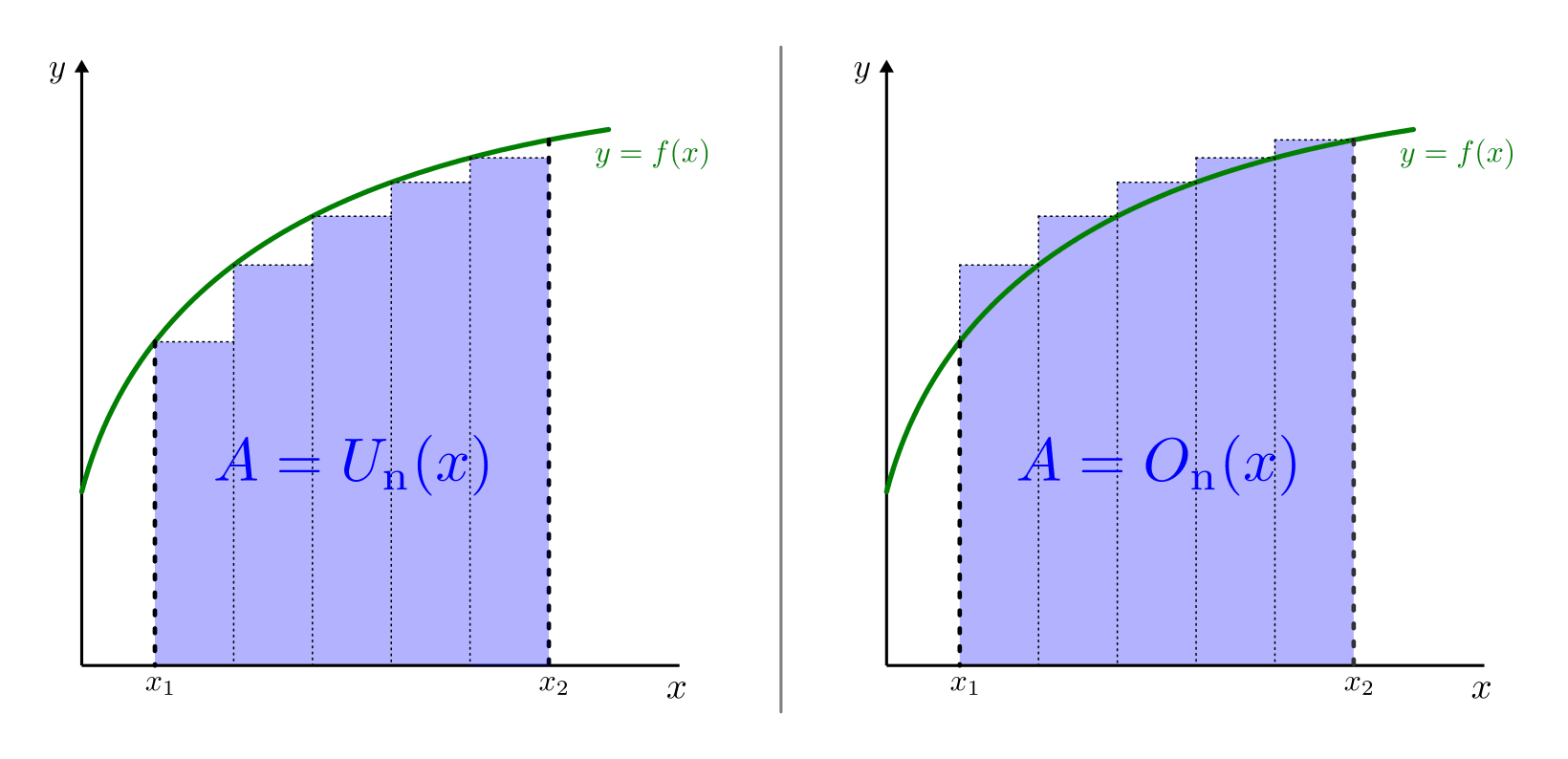
Untersumme und Obersumme als Näherungen für den Flächeninhalt zwischen einem
Funktionsgraphen und der  -Achse.
-Achse.
Je nachdem, ob man als Höhe jedes Rechtecks jeweils den kleineren oder größeren
der Funktionswerte beider Randpunkte wählt, füllen die Rechtecke die Fläche
unterhalb des Funktionsgraphen entweder nicht ganz aus, oder sie ragen stets an
einer Seite über den Funktionsgraphen hinaus. Die Summen der so gewählten
Rechteck-Flächen werden dementsprechend als Untersumme 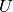 bzw. Obersumme
bzw. Obersumme
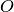 bezeichnet. Für
bezeichnet. Für  Unterteilungen mit einer Breite von jeweils
Unterteilungen mit einer Breite von jeweils
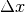 gilt:
gilt:
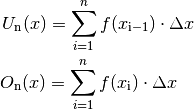
Für die Fläche ![A_{\mathrm{[x_1; x_2]}} \left( f(x) \right)](../_images/math/c17baa38c751a4d9e960801568a7026451426322.png) unterhalb des
Funktionsgraphen
unterhalb des
Funktionsgraphen 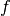 zwischen den zwei Punkten
zwischen den zwei Punkten 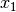 und
und 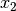 gilt somit:[1]
gilt somit:[1]
![U _{\mathrm{n}}(x) \; \le \; A _{\mathrm{[x_1;x_2]}}\left( f(x)\right) \;
\le \; O _{\mathrm{n}}(x)](../_images/math/96dbfe9346953b7864f70d4feedfb68ebc3481aa.png)
Unterteilt man bei einer beliebigen Funktion den Bereich zwischen 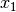 und
und 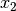 in eine größere Zahl an schmaleren Rechtecken, so lassen sich
die Abweichungen der einzelnen Rechteckshöhen von den jeweiligen Funktionswerten
verringern und damit die Werte der Unter- und Obersumme angleichen. Bei einer
(theoretischen) Unterteilung in unendlich viele, dafür beliebig schmale
Rechtecke haben die Unter- und Obersumme den gleichen Grenzwert, der mit der
gesuchten Fläche
in eine größere Zahl an schmaleren Rechtecken, so lassen sich
die Abweichungen der einzelnen Rechteckshöhen von den jeweiligen Funktionswerten
verringern und damit die Werte der Unter- und Obersumme angleichen. Bei einer
(theoretischen) Unterteilung in unendlich viele, dafür beliebig schmale
Rechtecke haben die Unter- und Obersumme den gleichen Grenzwert, der mit der
gesuchten Fläche ![A_{\mathrm{[x_1; x_2]}} \left( f(x) \right)](../_images/math/c17baa38c751a4d9e960801568a7026451426322.png) identisch ist.
identisch ist.
Mathematisch wird die Annäherung der Ober- und Untersumme bei unendlich vielen,
infinitessimal kleinen Unterteilungen durch das so genannte Integralzeichen
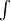 anstelle von
anstelle von  gekennzeichnet. Zudem wird
anstelle von
gekennzeichnet. Zudem wird
anstelle von 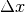 für die Breite jedes einzelnen Rechtecks
für die Breite jedes einzelnen Rechtecks
 geschrieben:
geschrieben:
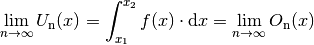
Der Ausdruck 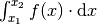 wird dabei
Integral von
wird dabei
Integral von  über
über ![[x_1 ; x_2]](../_images/math/e85537b2f998a7d364a0d4c3e2160342904c3d23.png) genannt. Die Funktion
genannt. Die Funktion
 wird als Integrand und
wird als Integrand und 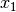 bzw.
bzw. 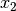 als
Integrationsgrenzen bezeichnet.
als
Integrationsgrenzen bezeichnet.
Integrierbarkeit und Stammfunktion¶
Ein Integral 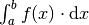 einer Funktion
einer Funktion
 über das Intervall
über das Intervall ![[a;b]](../_images/math/b5068dc3def8ee5fff90adf85e67be191f67196f.png) lässt sich immer dann eindeutig
berechnen, wenn die Funktion stetig ist, der Funktionsgraph
also keine Sprünge aufweist. Das gleiche gilt für bereichsweise definierte
Funktionen, die in den einzelnen Bereichen Stetigkeit aufweisen und
beschränkt sind, also keine Unendlichkeitsstellen
besitzen. Jede Funktion, die diese Bedingung erfüllt, wird integrierbar genannt.
lässt sich immer dann eindeutig
berechnen, wenn die Funktion stetig ist, der Funktionsgraph
also keine Sprünge aufweist. Das gleiche gilt für bereichsweise definierte
Funktionen, die in den einzelnen Bereichen Stetigkeit aufweisen und
beschränkt sind, also keine Unendlichkeitsstellen
besitzen. Jede Funktion, die diese Bedingung erfüllt, wird integrierbar genannt.
Der Wert eines Integrals 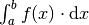 lässt sich
am einfachsten berechnen, wenn man zur gegebenen Funktion
lässt sich
am einfachsten berechnen, wenn man zur gegebenen Funktion  eine so
genannte „Stammfunktion“
eine so
genannte „Stammfunktion“ 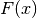 findet. Eine solche Stammfunktion hat die
Eigenschaft, dass ihre erste Ableitung
findet. Eine solche Stammfunktion hat die
Eigenschaft, dass ihre erste Ableitung 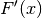 gerade der ursprünglichen
Funktion
gerade der ursprünglichen
Funktion  entspricht. Als Zusammenhang zwischen der Stammfunktion
und der zu integrierenden Funktion gilt für alle
entspricht. Als Zusammenhang zwischen der Stammfunktion
und der zu integrierenden Funktion gilt für alle ![x \in [a;b]](../_images/math/31dfceebccaa84a62e388450b1549db071aa0d4f.png) also:
also:
(1)¶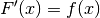
Die Integration kann also als Umkehrung der Differentiation angesehen werden.
Während jedoch das Ableiten einer Funktion stets ein eindeutiges Ergebnis
liefert, ist die Bestimmung der Stammfunktion nicht eindeutig: Ist 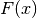 eine Stammfunktion von
eine Stammfunktion von  , so ist jede Funktion
, so ist jede Funktion  mit
einer additiven Konstante
mit
einer additiven Konstante 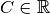 ebenfalls eine Stammfunktion
von
ebenfalls eine Stammfunktion
von  , da ein konstanter Term beim Ableiten stets den Wert Null
ergibt. Die Gesamtheit aller Stammfunktionen wird „unbestimmtes Integral“
genannt und mittels
, da ein konstanter Term beim Ableiten stets den Wert Null
ergibt. Die Gesamtheit aller Stammfunktionen wird „unbestimmtes Integral“
genannt und mittels 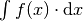 , also ohne
konkrete Integrationsgrenzen geschrieben.
, also ohne
konkrete Integrationsgrenzen geschrieben.
Anfangsbedingung und Integralfunktion
Aus der Menge aller Stammfunktionen soll üblicherweise eine bestimmt werden,
die durch einen gegebenen Punkt 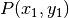 verläuft. Eine solche
Forderung nennt man Anfangsbedingung.
verläuft. Eine solche
Forderung nennt man Anfangsbedingung.
Soll das Integral von einer festen Grenze  bis zu einer variablen
Grenze
bis zu einer variablen
Grenze  verlaufen, so ist das Integral gleich Null, wenn
verlaufen, so ist das Integral gleich Null, wenn  ist, da in diesem Fall keine Fläche aufgespannt wird. Die Anfangsbedingung
besteht somit darin, dass die Stammfunktion an der Stelle
ist, da in diesem Fall keine Fläche aufgespannt wird. Die Anfangsbedingung
besteht somit darin, dass die Stammfunktion an der Stelle  eine
Nullstelle aufweisen muss. Es muss also gelten:
eine
Nullstelle aufweisen muss. Es muss also gelten:
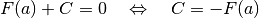
Dieser Gedanke folgt daraus, dass man 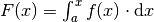 als so genannte Integralfunktion interpretiert, die jeweils den
Wert des Integrals liefert, wenn die untere Grenze
als so genannte Integralfunktion interpretiert, die jeweils den
Wert des Integrals liefert, wenn die untere Grenze  und die oberen
Grenze
und die oberen
Grenze  entspricht. Mit der obigen Anfangsbedingung erhält man somit
als Wert für das bestimmte Integral über die Funktion
entspricht. Mit der obigen Anfangsbedingung erhält man somit
als Wert für das bestimmte Integral über die Funktion  von
von
 bis
bis 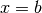 :
:
(2)¶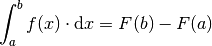
Als Kurzschreibweise ist hierbei 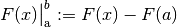 üblich. Möchte man das Integral über eine Funktion
üblich. Möchte man das Integral über eine Funktion  zwischen
zwei bestimmten Grenzen
zwischen
zwei bestimmten Grenzen  und
und 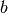 berechnen, so genügt es also,
die Stammfunktion zu bestimmen, die Werte
berechnen, so genügt es also,
die Stammfunktion zu bestimmen, die Werte  und
und 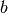 in die
Stammfunktion einzusetzen und die Differenz beider Werte zu berechnen:
in die
Stammfunktion einzusetzen und die Differenz beider Werte zu berechnen:
(3)¶
Die Schwierigkeit bei der Integralrechnung besteht folglich darin, eine
Stammfunktion 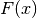 zur gegebenen Funktion
zur gegebenen Funktion  zu finden.
zu finden.
Grundintegrale¶
Von den elementaren Funktionen sowie einigen Kombinationen dieser Funktionen gibt es unmittelbare Lösungsformeln zur Bestimmung der jeweiligen Stammfunktion.
Integralregeln für Potenz- und Wurzelfunktionen
Ist die Funktion
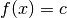 mit
mit 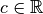 eine konstante
Funktion, so gilt für die Stammfunktion
eine konstante
Funktion, so gilt für die Stammfunktion 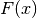 :
:(4)¶
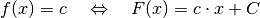
Anschaulich entspricht der Wert von
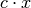 der Fläche des Rechtecks
mit der Breite
der Fläche des Rechtecks
mit der Breite  , das zwischen der konstanten Funktion und der
, das zwischen der konstanten Funktion und der
 -Achse liegt und die Länge
-Achse liegt und die Länge  hat.
hat.Ist die Funktion
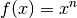 eine allgemeine Potenzfunktion mit der Einschränkung
eine allgemeine Potenzfunktion mit der Einschränkung 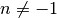 , so
gilt für die Stammfunktion
, so
gilt für die Stammfunktion 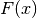 :
:(5)¶
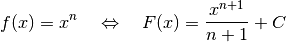
Dieses Ergebnis folgt daraus, dass die Ableitung der Funktion
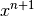 dem Term
dem Term 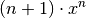 entspricht. Die ursprüngliche Funktion
entspricht. Die ursprüngliche Funktion
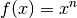 unterscheidet sich lediglich um den Faktor
unterscheidet sich lediglich um den Faktor
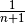 von diesem Ableitungsterm.
von diesem Ableitungsterm.Ist beispielsweise
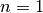 , also
, also 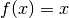 , so ist
, so ist 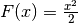 eine Stammfunktion. Anschaulich entspricht der Term
eine Stammfunktion. Anschaulich entspricht der Term
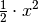 der Fläche eines Dreiecks, das zwischen dem
Graphen
der Fläche eines Dreiecks, das zwischen dem
Graphen  und der
und der  -Achse liegt; diese Fläche ist gleich
der Hälfte der Quadratfläche von
-Achse liegt; diese Fläche ist gleich
der Hälfte der Quadratfläche von 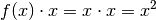 .
.Integrale von linearen Funktionen treten in den Naturwissenschaften häufig auf, beispielsweise gilt für die zurückgelegte Wegstrecke
 bei einer
Bewegung mit konstanter Beschleunigung
bei einer
Bewegung mit konstanter Beschleunigung  , wobei in diesem Fall die
Integrationsvariable die Zeit
, wobei in diesem Fall die
Integrationsvariable die Zeit  ist. Weitere Beispiele sind die
Bewegungs- und Spannenergie, usw.
ist. Weitere Beispiele sind die
Bewegungs- und Spannenergie, usw.Die obige Integrationsregel (5) gilt wegen des Zusammenhangs
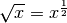 auch für
Wurzelfunktionen. Beispielsweise gilt im Fall
auch für
Wurzelfunktionen. Beispielsweise gilt im Fall
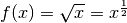 mit
mit 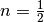 :
: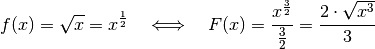
Ist
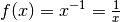 mit
mit 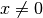 , so ist eine
Anwendung der obigen Regel (5) nicht
möglich. Für diesen Sonderfall gilt vielmehr folgender Zusammenhang:
, so ist eine
Anwendung der obigen Regel (5) nicht
möglich. Für diesen Sonderfall gilt vielmehr folgender Zusammenhang:
Die Stammfunktion der Hyperbelfunktion
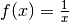 ist also die natürliche Logarithmusfunktion
ist also die natürliche Logarithmusfunktion 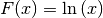 .[2]
.[2]
Integralregeln für Exponentialfunktionen
Ist
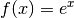 mit
mit 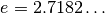 als Eulerscher Zahl, so
gilt für die Stammfunktion
als Eulerscher Zahl, so
gilt für die Stammfunktion 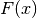 :
:(6)¶
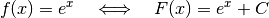
Ebenso wie die natürliche Exponentialfunktion beim Ableiten unverändert bleibt, so bleibt sie auch beim Integrieren unverändert.
Ist
 mit
mit 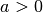 und
und 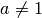 , so
gilt für die Stammfunktion
, so
gilt für die Stammfunktion 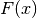 :
:(7)¶
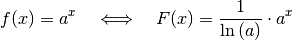
Auch die allgemeine Exponentialfunktion ergibt beim Integrieren wieder eine Exponentialfunktion, wobei der Vorfaktor
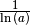 berücksichtigt werden muss.
berücksichtigt werden muss.
Integralregeln für trigonometrische Funktionen und Arcusfunktionen
Ist
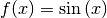 , so gilt für die Stammfunktion
, so gilt für die Stammfunktion 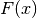 :
:(8)¶

Dieser Zusammenhang ergibt sich daraus, dass die Ableitung der Cosinusfunktion der negativen Sinusfunktion entspricht.
Ist
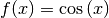 , so gilt für die Stammfunktion
, so gilt für die Stammfunktion 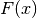 :
:(9)¶

Dieser Zusammenhang ergibt sich daraus, dass die Ableitung der Sinusfunktion der Cosinusfunktion entspricht.
Zusammenfassung wichtiger Integrationsregeln¶
Für jedes Integral gelten folgende Eigenschaften:
Vertauscht man die obere und die untere Integrationsgrenze, so ändert das Integral sein Vorzeichen:
(10)¶
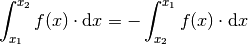
Der Grund dafür liegt darin, dass hierbei die Breiten aller Rechtecke
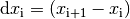 für
für  ein negatives Vorzeichen bekommen und somit bei der
Auswertung des Integrals über gleich große, aber negative Werte summiert wird.
ein negatives Vorzeichen bekommen und somit bei der
Auswertung des Integrals über gleich große, aber negative Werte summiert wird.Ist die obere Integrationsgrenze
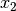 gleich der unteren Grenze
gleich der unteren Grenze
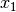 , so ist das Integral für jede beliebige Funktion
, so ist das Integral für jede beliebige Funktion  gleich Null:
gleich Null:(11)¶
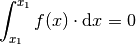
Anschaulich lässt sich dies dadurch erklären, dass die Fläche zwischen
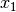 und
und 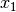 eine Breite von Null hat.
eine Breite von Null hat.Jedes Integral lässt sich auf folgende Weise in zwei Teilintegrale zerlegen:
(12)¶
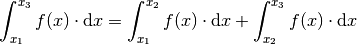
Ist
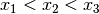 , so ist umittelbar einleuchtend, dass die Fläche
zwischen
, so ist umittelbar einleuchtend, dass die Fläche
zwischen 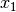 und
und 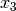 gleich der Summe der Teilflächen sein
muss, da sich das Intervall
gleich der Summe der Teilflächen sein
muss, da sich das Intervall ![[x_1 ; x_3]](../_images/math/ec135b4d8d96c6ba57ad182328592f86cc2be46d.png) in zwei Teilintegrale
in zwei Teilintegrale
![[x_1;x_2] \cup [x_2;x_3]](../_images/math/cff95a1d4e28c4b426e3fadd6c92ff747f94d93e.png) zerlegen lässt und die entsprechenden
Teilsummen gebildet werden können.
zerlegen lässt und die entsprechenden
Teilsummen gebildet werden können.Die Regel gilt jedoch auch dann, wenn
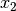 außerhalb von
außerhalb von
![[x_1;x_3]](../_images/math/9cac197c3df1dde8e0ac2fe5381e50001986b1dd.png) liegt; ist beispielsweise
liegt; ist beispielsweise 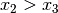 , so wird die –
gegenüber dem Gesamtintegral – mit dem ersten Teilintervall zusätzlich
addierte Fläche aufgrund der Vorzeichenregel
(10) durch das zweite (negative) Teilintegral
wieder subtrahiert.
, so wird die –
gegenüber dem Gesamtintegral – mit dem ersten Teilintervall zusätzlich
addierte Fläche aufgrund der Vorzeichenregel
(10) durch das zweite (negative) Teilintegral
wieder subtrahiert.Lässt sich eine zu integrierende Funktion als Summe zweier Funktion
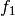 und
und 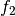 darstellen, so ist das Ergebnis gleich der Summe
der Integrale beider Funktionen:
darstellen, so ist das Ergebnis gleich der Summe
der Integrale beider Funktionen:(13)¶
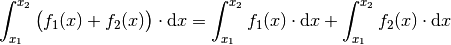
Die obige Regel entspricht formal dem Distributivgesetz.
Lässt sich eine zu integrierende Funktion als Produkt einer Funktion
 und eines konstanten Faktors
und eines konstanten Faktors  darstellen, so kann dieser
vor das Integral gezogen werden:
darstellen, so kann dieser
vor das Integral gezogen werden:(14)¶
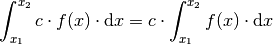
Die obige Regel entspricht dem Assoziativgesetz der Multiplikation. Anschaulich kann man sich jeden Funktionswert und damit die Höhe aller zu addierenden Rechtecke um den Faktor
 gestreckt denken.
gestreckt denken.Erfüllen zwei Funktionen
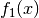 und
und  für jeden
beliebigen Wert
für jeden
beliebigen Wert  innerhalb des Intervalls
innerhalb des Intervalls ![[x_1;x_2]](../_images/math/8d5e17d87f512f7db23d090918796355d3ddc7a2.png) die
Bedingung
die
Bedingung 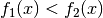 , so gilt:
, so gilt:![f_1(x) < f_2(x) \text{ für alle } x \in [x_1;x_2] \quad \Leftrightarrow
\quad \int_{x_1}^{x_2} f_1(x) < \int_{x_1}^{x_2} f_2(x)](../_images/math/de24347047eafc960ee762a7735bcc0dcb3ede21.png)
Bestimmung der Fläche zwischen zwei Graphen
Mittels der Integralrechnung kann nicht nur die Fläche zwischen einem
Funktionsgraph und der  -Achse, sondern auch die zwischen zwei
Funktionsgraphen
-Achse, sondern auch die zwischen zwei
Funktionsgraphen 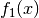 und
und  in einem Intervall
in einem Intervall
![[a;b]](../_images/math/b5068dc3def8ee5fff90adf85e67be191f67196f.png) eingeschlossene Fläche berechnet werden. Verläuft der Graph von
eingeschlossene Fläche berechnet werden. Verläuft der Graph von
 oberhalb des Graphen von
oberhalb des Graphen von 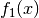 , gilt also
, gilt also 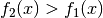 für alle
für alle ![x \in [a;b]](../_images/math/31dfceebccaa84a62e388450b1549db071aa0d4f.png) , so entspricht die gesuchte Fläche
folgendem Integral:[3]
, so entspricht die gesuchte Fläche
folgendem Integral:[3]
(15)¶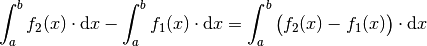
Schneiden sich Schnittpunkte zweier Funktionen, so müssen zunächst die Schnittstellen berechnet werden; anschließend kann einzeln von Schnittstelle zu Schnittstelle integriert werden. In jedem einzelnen Teilintervall wird dabei die Funktion mit den niedrigeren Funktionswerten von der Funktion mit den höheren Funktionswerten subtrahiert.
Integrationsmethoden¶
In vielen Fällen, insbesondere bei zusammengesetzten Funktionen, lässt sich eine Integration nicht mittels der oben genannten Grundintegrale durchführen. In solchen Fällen können allerdings oftmals weitere Integrationsmethoden angewendet werden.
Partielle Integration
Die Methode der partiellen Integration entspricht formal einer umgekehrten Anwendung der Produktregel bei Ableitungen:
(16)¶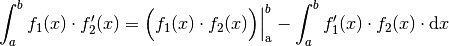
Diese Methode kann immer dann genutzt werden, wenn die zu integrierende Funktion
als Produkt zweier Teilfunktionen geschrieben werden kann. Lässt sich eine
dieser Funktionen leicht integrieren, so setzt man diese als 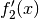 ;
die andere Teilfunktion, die sich möglichst leicht ableiten lassen sollte, wird
als
;
die andere Teilfunktion, die sich möglichst leicht ableiten lassen sollte, wird
als 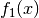 gesetzt. Das Integral kann dann berechnet werden, indem man
zunächst als Zwischenergebnis das Produkt von
gesetzt. Das Integral kann dann berechnet werden, indem man
zunächst als Zwischenergebnis das Produkt von 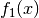 und der
Stammfunktion von
und der
Stammfunktion von 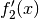 bildet, die obere und untere
Integrationsgrenze als
bildet, die obere und untere
Integrationsgrenze als  -Werte einsetzt und beide Werte voneinander
subtrahiert. Anschließend muss das Integral
-Werte einsetzt und beide Werte voneinander
subtrahiert. Anschließend muss das Integral  berechnet werden und dessen Wert vom Zwischenergebnis
subtrahiert werden.
berechnet werden und dessen Wert vom Zwischenergebnis
subtrahiert werden.
Die Methode der partiellen Integration wird insbesondere dann verwendet, wenn
eine der beiden Teilfunktionen eine Potenzfunktion  mit
mit 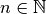 ist. Bei einer derartigen Funktion ist die
ist. Bei einer derartigen Funktion ist die  -te Ableitung
ein konstanter Wert, der beim Integrieren gemäß Gleichung
(14) als konstanter Faktor vor das Integral
gezogen werden kann. Gegebenenfalls muss folglich die Methode der partiellen
Integration wiederholt angewendet werden (maximal
-te Ableitung
ein konstanter Wert, der beim Integrieren gemäß Gleichung
(14) als konstanter Faktor vor das Integral
gezogen werden kann. Gegebenenfalls muss folglich die Methode der partiellen
Integration wiederholt angewendet werden (maximal  mal), um die jeweils
auf der rechten Seite stehenden (Teil-)Integrale der Form
mal), um die jeweils
auf der rechten Seite stehenden (Teil-)Integrale der Form 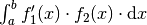 schrittweise zu berechnen.
schrittweise zu berechnen.
Integration durch Substitution
Die Methode der Integration durch Substitution entspricht formal einer umgekehrten Anwendung der Kettenregel bei Ableitungen:
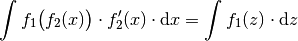
Hierbei wurde 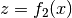 geschrieben. Man kann mit dieser Substitution
nach einer Stammfunktion
geschrieben. Man kann mit dieser Substitution
nach einer Stammfunktion 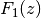 von
von 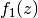 suchen, in gleicher
Weise als würde man lediglich
suchen, in gleicher
Weise als würde man lediglich  anstelle von
anstelle von  schreiben und
somit eine Stammfunktion
schreiben und
somit eine Stammfunktion 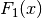 zu
zu 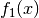 suchen. Hat man eine
solche Stammfunktion
suchen. Hat man eine
solche Stammfunktion 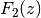 gefunden, so genügt es, bei dieser
Stammfunktion wiederum
gefunden, so genügt es, bei dieser
Stammfunktion wiederum  durch den Ausdruck
durch den Ausdruck  zu ersetzen.
zu ersetzen.
Möchte man mit dieser Methode ein bestimmtes Integral von  bis
bis
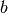 berechnen, so müssen allerdings auch die Integralgrenzen umgerechnet
werden. Es gilt:
berechnen, so müssen allerdings auch die Integralgrenzen umgerechnet
werden. Es gilt:

Da  bekannt ist, müssen lediglich die Integrationsgrenzen in
diese Funktion eingesetzt werden, um die neuen Integrationsgrenzen zu erhalten.
bekannt ist, müssen lediglich die Integrationsgrenzen in
diese Funktion eingesetzt werden, um die neuen Integrationsgrenzen zu erhalten.
Integrale der Form 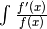
Soll das Integral einer zusammengesetzten Funktion berechnet werden, deren Zähler der Ableitung des Nenners entspricht, so kann folgende Regel verwendet werden:

Hat die Funktion  im Intervall
im Intervall ![[a;b]](../_images/math/b5068dc3def8ee5fff90adf85e67be191f67196f.png) keine Nullstelle, so
gilt für das bestimmte Integral über
keine Nullstelle, so
gilt für das bestimmte Integral über  von
von  bis
bis 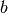 :
:
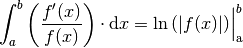
Weitere Integrale können Integraltabellen entnommen werden, beispielsweise Integraltabelle (HS Esslingen).
Anmerkungen:
| [1] | Das Gleichheitszeichen in der obigen Gleichung gilt nur für konstante
 -Werte, also Funktionen der Form -Werte, also Funktionen der Form 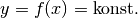 |
| [2] | Auch in diesem Fall ist die Integration die Umkehrung der
Differentiation, denn die Ableitung der natürlichen
Logarithmusfunktion 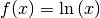 ist gerade ist gerade 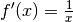 . . |
| [3] | Formal ist Gleichung (15) zur Berechnung der Fläche zwischen zwei Funktionsgraphen mit Gleichung (13) als Distributivgesetz der Integralrechnung identisch. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

![[x1;x2]](../_images/math/7ca778a3e11504571d8cae0216a80afdda40041f.png) .
.