Aufgaben zur Wärmelehre¶

Temperatur und Wärme¶

Die folgenden Aufgaben beziehen sich auf den Abschnitt#Temperatur und W��rme.

(*) Wie viel Grad Fahrenheit entsprechen einer Temperatur von $\unit[20]{\degree C}$ ?

Lösung

(*) Ab einer Körpertemperatur von über $\unit[40]{\degree C }$ spricht man bei einem Menschen von „hohem Fieber“. Wie viel Kelvin beziehungsweise Grad Fahrenheit entsprechen dieser Temperatur?

Lösung

Die folgenden Aufgaben beziehen sich auf den Abschnitt Wärmekapazität und Phasenübergänge.

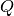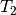(**) Welche Wärmemenge $Q$ ist nötig, um $m=\unit[5]{kg}$ Eis mit einer Temperatur von $T=\unit[0]{\degree C}$ und einer spezifischen Schmelzwärme von $q_{\mathrm{s}} = \unit[334]{kJ/kg}$ zu schmelzen? Auf welche Temperatur $T_2$ könnten $m=\unit[5]{kg}$ Wasser mit einer Temperatur von $T_1 = \unit[0]{\degree C}$ und einer spezifischen Wärmemenge von $c = \unit[4,2]{\frac{kJ}{kg \cdot K}}$ mit der gleichen Wärmemenge erwärmt werden?

Lösung

(**) Wie viel Energie ist mindestens notwendig, um $V=\unit[3,0]{l}$ Wasser mit einer spezifischen Wärmekapazität von $\unit[4,2]{\frac{KJ}{kg \cdot K}}$ zum Sieden zu bringen, wenn die Temperatur des Wassers zunächst $\unit[20]{\degree C}$ beträgt? Wie lange dauert dieser Vorgang mindestens, wenn die Heizleistung $\unit[2,0]{kW}$ beträgt? (Wärmeverluste sollen bei dieser Aufgabe vernachlässigt werden.)

Lösung

Die folgenden Aufgaben beziehen sich auf den Abschnitt Ausbreitung von Wärme.

(*) Wie groß ist der Wärmestrom 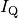$I_{\mathrm{Q}}$ durch ein $\unit[1]{m^2}$ großes Fenster mit einfacher, $\unit[4]{mm}$ dicker Verglasung (Wärmeleitfähigkeit $\lambda = \unit[1]{\frac{W}{m \cdot K}}$ ), wenn die Temperatur an der Innenseite $\unit[20]{\degree C}$ und an der Außenseite $\unit[5]{\degree C}$ beträgt?

Lösung

(**) Wie groß ist der Wärmestrom 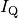$I_{\mathrm{Q}}$ durch ein $A=\unit[2]{m^2}$ großes Fenster mit doppelter Verglasung (Dicke der Scheiben je $\unit[4]{mm}$ , Wärmeleitfähigkeit $\lambda = \unit[1]{\frac{W}{m \cdot K}}$ ), zwischen denen ein $\unit[1]{cm}$ breiter Luftspalt mit einer Wärmeleitfähigkeit von $\lambda_2 = \unit[0,025]{\frac{W}{m \cdot K}}$ liegt? Die Temperatur an der Innenseite beträgt wiederum $\unit[20]{\degree C}$ und an der Außenseite $\unit[5]{\degree C}$ .

Lösung

(**) Um welchen Faktor steigt die Leistung der Wärmestrahlung eines schwarzen Körpers, wenn man seine Oberflächentemperatur verdoppelt? Um welchen Faktor steigt die Strahlungsleistung, wenn die Oberflächentemperatur von $T_1 = \unit[10]{\degree C}$ auf $T_2 = \unit[40]{\degree C}$ erhöht wird?

Lösung

Die folgenden Aufgaben beziehen sich auf den Abschnitt Ausdehnung bei Erwärmung.

(*) Im Hochsommer wird ein Lineal aus Metall in der Sonne liegen gelassen und erwärmt sich. Kann man das erhitzte Lineal weiterhin – trotz der Ausdehnung bei Erwärmung – zur Längenmessung verwenden?

Lösung

(*) Ein Bimetall-Streifen besteht aus zwei aufeinander gewälzten Blechstreifen, beispielsweise aus Aluminium $(\alpha_{\mathrm{Al}} = \unit[0,024]{\frac{mm}{m \cdot K}})$ und Chrom-Stahl $(\alpha_{\mathrm{FeCr}} = \unit[0,010]{\frac{mm}{m \cdot K}})$ . In einem Bügeleisen soll sich der Bimetallstreifen bei ausreichender Erwärmung nach oben verbiegen und die Heizung unterbrechen. Welches Metall muss oben, welches unten liegen?

Lösung

(*) Wie lang wird ein $l=\unit[120]{m}$ langer Kupferdraht $(\alpha_{\mathrm{Cu}} = \unit[0,0168]{\frac{mm}{m \cdot K} })$ , wenn er um $\Delta T = \unit[50]{K}$ erhitzt wird?

Lösung

(*) Welchen Längenschwankungen ist eine bei einer Temperatur von $T_1=\unit[15]{\degree C}$ insgesamt $l_1 = \unit[300]{m}$ lange Brücke aus Beton $(\alpha_{\mathrm{Beton}} = \unit[12 \cdot 10^{-6}]{\frac{1}{K}})$ unterworfen, wenn sie im Winter auf $T_2=\unit[-15]{\degree C}$ abkühlt beziehungsweise sich im Sommer auf $T_3=\unit[40]{\degree C}$ erhitzt?

Lösung

(*) An einem Sommertag scheint die Sonne auf einen Tank aus Stahl $(\alpha = \unit[11,8 \cdot 10^{-6}]{\frac{1}{K}})$ mit einem Volumen von $V_0=\unit[50]{l}$ ; der Tank erhitzt sich dabei von $T_0=\unit[15]{\degree C}$ auf $\unit[50]{\degree C}$ . Auf welches Volumen dehnt sich der Tank aus? Um welches Volumen würde sich ein gleiches Volumen an Benzin $(\gamma = \unit[1,06 \cdot 10 ^{-3}]{\frac{1}{K}})$ bei gleicher Temperaturdifferenz ausdehnen?

Lösung

(*) Inwiefern verhält sich Wasser bei der Ausdehnung durch Erwärmung anders als andere Flüssigkeiten?

Lösung

(*) Warum erhitzt sich beim Zusammendrücken einer Luftpumpe die Luft (und damit auch die Luftpumpe)? Wie lässt sich dieser Effekt mit Hilfe des Teilchenmodells erklären?

Lösung

(**) Wie verändert sich die Molekülbewegung eines idealen Gases bei der Abkühlung bis zum absoluten Nullpunkt? Was passiert mit realen Gasen, bevor sie den absoluten Nullpunkt erreichen?

Lösung

(**) Ein Gas mit einem Volumen von $V_1 = \unit[30]{cm^3}$ , einem Druck $p_1 = \unit[1]{bar \, (abs)}$ und einer Temperatur $T_1 = \unit[300]{K}$ wird erwärmt. Dabei steigt seine Temperatur auf $T_2 = \unit[500]{K}$ ; gleichzeitig wird der Druck auf $p_2 = \unit[4]{bar \, (abs.)}$ erhöht. Welches Volumen nimmt das Volumen nach dieser Zustandsänderung an?

Lösung

(*) Ein ungeheiztes Zimmer mit einer Fläche von $\unit[20]{m^2}$ und einer Höhe von $\unit[2,5]{m}$ wird im Winter von $T_1 = \unit[12]{\degree C}$ auf $T_2 = \unit[20]{\degree C}$ aufgeheizt. Wie viel Luft muss dabei aus dem Zimmer entweichen, wenn der Luftdruck während der Erwärmung konstant bleibt?

Lösung

(**) Ein Druckbehälter mit einem Volumen von $\unit[500]{l}$ ist mit Luft gefüllt, wobei der Überdruck $p_1=\unit[3 \cdot 10^5]{Pa}$ beträgt. Wieviel Luft mit einem normalen Atmosphärendruck $p_0 = \unit[1,0 \cdot 10^5]{Pa}$ müssen zusätzlich in den Behälter gepumpt werden, damit ein Überdruck von $p_2=\unit[8 \cdot 10^5]{Pa}$ entsteht?

Lösung

Die folgenden Aufgaben beziehen sich auf den Abschnitt Allgemeine Gasgleichung.

(**) Wie viele Moleküle sind ungefähr in $V=\unit[1,0]{l}$ Luft unter Normbedingungen enthalten?

Lösung

(**) Wie groß ist die Dichte von Luft in einem Gefäß, wenn dieses bei einer Temperatur von $T = \unit[20]{\degree C}$ bis auf ein Ultrahochvakuum mit einem Restdruck von $p = \unit[1 \cdot 10 ^{-10}]{Pa}$ leergepumpt wird? Wie viele Teilchen befinden sich dabei in $V = \unit[1]{cm^3}$ dieses Restgases?

Lösung