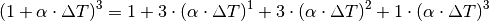Ausdehnung bei Erwärmung¶
Die meisten festen, flüssigen und gasförmigen Körper dehnen sich beim Erwärmen aus und ziehen sich beim Abkühlen zusammen. Gase dehnen sich bei Erwärmung am meisten, feste Stoffe am wenigsten aus.
Ausdehnung von Festkörpern¶
Ändert sich die Temperatur eines festen Körpers um einen bestimmten Betrag, so ändert sich entsprechend auch seine Länge beziehungsweise seine Fläche und sein Volumen. Mit steigender Temperatur nimmt die Länge zu, mit sinkender Temperatur nimmt die Länge ab.
Formel:
| Stoff | ![\alpha \text{ in } \unit[10 ^{-6}]{\frac{1}{K} }](../_images/math/1139583e59587f31357a06398acd2058d1e140cf.png) |
| Aluminium | 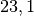 |
| Beton | 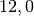 |
| Blei | 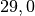 |
| Eisen | 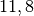 |
| Quarzglas | 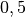 |
| Holz | 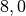 |
| Kupfer | 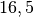 |
| Messing | 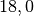 |
| Silber | 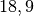 |
| Silicium | 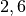 |
| Titan | 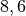 |
| Wolfram | 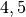 |
| Ziegel | 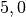 |
| Zinn | 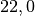 |
Beispiel:
Eine
![l= \unit[10]{m}](../_images/math/4a1877a4977cc2b70e7d7167a16983739fa6f9d5.png) lange Eisenstange wird um
lange Eisenstange wird um ![\Delta T=
\unit[50]{K}](../_images/math/f5ce9eab2844943a64ce13ed56ade50bb5773833.png) erwärmt. Mit dem thermischen Längenausdehnungskoeffizient
erwärmt. Mit dem thermischen Längenausdehnungskoeffizient
![\alpha_{\mathrm{Fe}} = \unit[11,8 \cdot 10 ^{-6}]{\frac{1}{K}}](../_images/math/34a9c85e172bba4433de57aca49507b82841fb20.png) lässt sich
die Längenänderung der Stange berechnen:
lässt sich
die Längenänderung der Stange berechnen:![\Delta l = \alpha_{\mathrm{Stahl}} \cdot \Delta T \cdot l = \unit[11,8 \cdot
10 ^{-6}]{\frac{1}{K}} \cdot \unit[50]{K} \cdot \unit[10]{m} \approx
\unit[0,006]{m}](../_images/math/4f6729038a44d9f80e214e790289365ed69baca0.png)
Die Längenausdehnung beträgt somit rund
![\unit[6]{mm}](../_images/math/315b6faf5b836dbd02d4b8fa29ea8cc0794bc475.png) .
.
Auf ähnliche Weise wie in Gleichung (2) kann
die neue Fläche 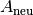 beziehungsweise das neue Volumen
beziehungsweise das neue Volumen 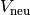 eines festen Körpers der Fläche
eines festen Körpers der Fläche  beziehungsweise des Volumens
beziehungsweise des Volumens
 bei einer Temperaturänderung um
bei einer Temperaturänderung um  berechnet werden.
Dabei geht man davon aus, dass sich der betrachtete Festkörper in alle
Richtungen gleich ausdehnt:[2]
berechnet werden.
Dabei geht man davon aus, dass sich der betrachtete Festkörper in alle
Richtungen gleich ausdehnt:[2]
![l_{\mathrm{neu}} &= l \cdot (1 + \alpha \cdot \Delta T) \\[6pt]
A_{\mathrm{neu}} &= A \cdot (1 + \alpha \cdot \Delta T)^2 \\[6pt]
V_{\mathrm{neu}} &= V \cdot (1 + \alpha \cdot \Delta T)^3](../_images/math/73717dd6d0ccc35e9611edc4f1a4bb8c8dac9ac5.png)
In sehr guter Näherung kann die Volumenausdehnung von Festkörpern auch folgendermaßen geschrieben werden:[3]
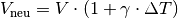
Hierbei ist 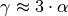 der so genannte
Volumen-Ausdehnungskoeffiezient.
der so genannte
Volumen-Ausdehnungskoeffiezient.
Im Wesentlichen ist temperaturbedingte Längen- beziehungsweise Volumenzunahme eines Festkörpers darauf zurückzuführen, dass die Atome beziehungsweise Moleküle des Festkörpers mit zunehmender Temperatur stärker um ihre Ruhelage schwingen. Dadurch vergrößern sich die Abstände zwischen den einzelnen Teilchen, und das Volumen des Körpers nimmt zu; zugleich nehmen die Kohäsionskräfte, welche die Atome beziehungsweise Moleküle des Festkörpers zusammen halten, geringer.
In der Technik versucht man geeignete Materialkombinationen zu nutzen, um mechanische Spannungen aufgrund von (unterschiedlich starken) Wärmeausdehnungen zu vermeiden. Beispielsweise werden in den Übergangskonstruktionen von Brücken Dehnungsfugen und Gleitlager eingesetzt, um temperaturbedingte Spannungen zu minimieren.
Ausdehnung von Flüssigkeiten¶
Ändert sich die Temperatur einer Flüssigkeit um einen bestimmten Betrag, so ändert sich entsprechend auch ihr Volumen. Mit steigender Temperatur nimmt das Volumen zu, mit sinkender Temperatur nimmt das Volumen ab.
Formel:
Die Volumenänderung
einer Flüssigkeit des Volumens
ist proportional zur Temperaturänderung
sowie zum (vom Stoff abhängigen) thermischen Volumenausdehnungskoeffizient
:
(3)¶
| Stoff | ![\gamma \text{ in } \unit[10 ^{-3}]{\frac{1}{K} }](../_images/math/172f6c23115b47f79bec502d230b507b98c83dc0.png) |
| Aceton | 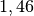 |
| Benzin | 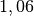 |
| Essigsäure | 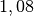 |
| Ethanol | 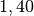 |
| Glycerin | 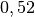 |
| Quecksilber | 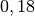 |
| Wasser | 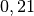 |
Im Wesentlichen ist temperaturbedingte Volumenzunahme von Flüssigkeiten darauf zurückzuführen, dass die Geschwindigkeit der Atome beziehungsweise Moleküle in der Flüssigkeit zunimmt. Die Teilchen beanspruchen so mehr Raum innerhalb der Flüssigkeit, das Volumen nimmt zu.
Ändert sich das Volumen einer bestimmten Flüssigkeitsmenge, so ändert sich auch die Dichte der Flüssigkeit.[4] Im Allgemeinen nimmt die Dichte von Flüssigkeiten mit wachsender Temperatur ab.
Formel:
Durch eine Temperaturänderung um
ändert sich die Dichte
einer Flüssigkeit umgekehrt proportional zum Volumenausdehnungskoeffizient
. Für die neue Dichte
der Flüssigkeit gilt:
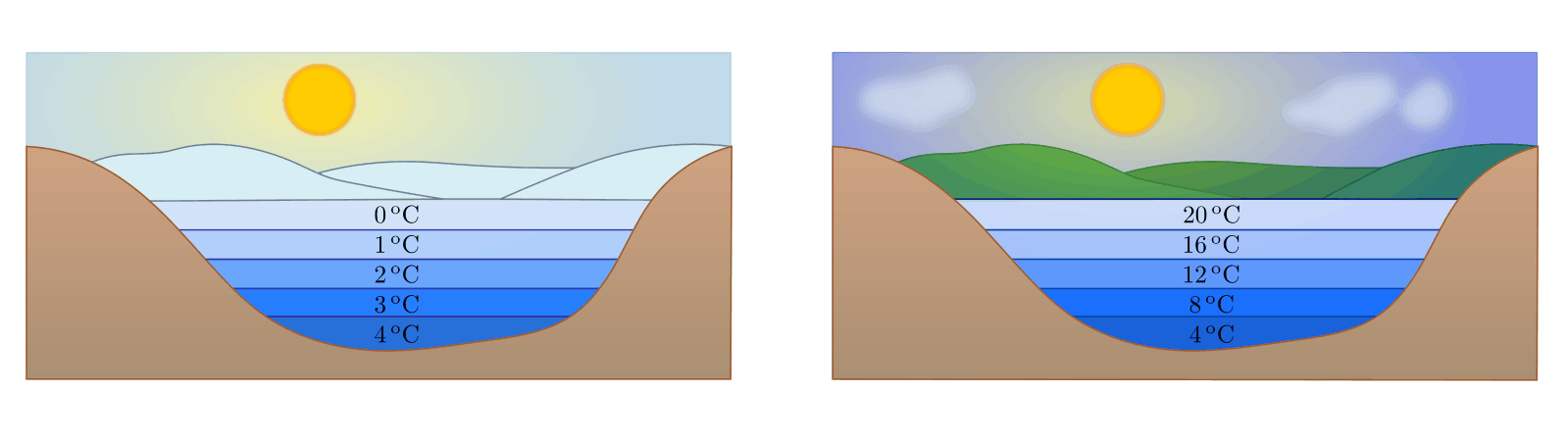
Die Anomalie des Wassers
Eine große Besonderheit („Anomalie“) des Wassers liegt darin, dass es bei
![\unit[4]{\degree C}](../_images/math/eed4ef41d7331125df384be9e18fd591c56a1acf.png) seine größte Dichte hat. Unterhalb dieser Temperatur
dehnt es sich wieder aus, bis es bei
seine größte Dichte hat. Unterhalb dieser Temperatur
dehnt es sich wieder aus, bis es bei ![\unit[0]{\degree C}](../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) zu Eis
erstarrt.
zu Eis
erstarrt.
Beispiel:
- Im Sommer ist die Oberfläche eines Sees warm. Die Temperatur sinkt mit zunehmender Tiefe.
- Im Herbst kühlt das Wasser an der Oberfläche ab und sinkt nach unten. Das
Tiefenwasser steigt empor und wird an der Oberfläche ebenfalls abgekühlt.
Schließlich herrscht überall im Wasser die Temperatur
![\unit[4]{\degree C}](../_images/math/eed4ef41d7331125df384be9e18fd591c56a1acf.png) .
. - Im Winter wird das Wasser an der Oberfläche weiter abgekühlt, sinkt aber nicht
mehr ab. Bei
![\unit[0]{\degree C}](../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) bildet sich an der Oberfläche des
Sees eine (isolierende) Eisdecke, die Wassertemperatur am Grund des Sees
beträgt weiterhin
bildet sich an der Oberfläche des
Sees eine (isolierende) Eisdecke, die Wassertemperatur am Grund des Sees
beträgt weiterhin ![\unit[4]{\degree C}](../_images/math/eed4ef41d7331125df384be9e18fd591c56a1acf.png) . Bei starkem und lang
anhaltendem Frost wird die Eisdecke zunehmend dicker; flache Gewässer können
dann von oben bis zum Grund gefrieren.
. Bei starkem und lang
anhaltendem Frost wird die Eisdecke zunehmend dicker; flache Gewässer können
dann von oben bis zum Grund gefrieren.
Eine zweite Besonderheit des Wassers liegt darin, dass es im erstarrten Zustand (Eis) eine geringere Dichte hat als im flüssigen Zustand. Dies hat einerseits zur Folge, dass Eis in Wasser schwimmt; andererseits dehnt sich Wasser beim Erstarren stark aus. Dabei kann es große Kräfte ausüben – mit Wasser gefüllte Gefäße können beim Gefrieren des Wassers platzen („Sprengwirkung“ des Eises). Bei Kraftfahrzeugen werden daher Frostschutzmittel in das Kühlwasser gemischt, welche die Erstarrungstemperatur absenken und ein Erstarren der Kühlflüssigkeit verhindern sollen.
Ausdehnung von Gasen¶
Bei Erwärmung dehnen sich Gase wesentlich stärker aus als Flüssigkeiten. Bleibt der Druck eines Gases während der Erwärmung konstant, so dehnt es sich proportional zur absoluten Temperatur aus.
Formel:
Bleibt der Druck
während einer Temperaturänderung konstant, so ist die Volumenänderung
eines Gases mit Volumen
proportional zur Temperaturänderung
sowie zum thermischen Volumenausdehnungskoeffizient
:
(4)¶
Dabei gilt in guter Näherung für alle Gase:
(5)¶
Der Volumenausdehnungskoeffizient
bei konstantem Druck ist somit näherungsweise für alle Gase gleich.
Beispiel:
Werden
![V = \unit[20]{l}](../_images/math/89cff7b8886ec41db2e962910c21763bd9822c25.png) Luft von
Luft von ![T_{\mathrm{0}} =
\unit[0]{\degree C }](../_images/math/9bf975575fc490ee65267fac7abf651d33b74c2f.png) auf
auf ![T_1 = \unit[10]{\degree C}](../_images/math/9050ba6af09a9ce18f3183f382d865cd0683ce3f.png) erwärmt,
so ändert sich das Volumen der Luft um
erwärmt,
so ändert sich das Volumen der Luft um![\Delta V = \gamma \cdot \Delta T \cdot V =
\unit[\frac{1}{273}]{\frac{1}{K} } \cdot \unit[10]{K} \cdot \unit[20]{l}
\approx \unit[0,73]{l}](../_images/math/93df690e2083b7ff7dafbb79bad98eff22249130.png)
Das Luftvolumen nimmt somit um etwa
![\unit[0,73]{l}](../_images/math/7e5e197f6e6434bfc721dc3517d89f5df05c722a.png) zu.
zu.
Die temperaturbedingte Volumenzunahme von Gasen ist – wie bei Flüssigkeiten – im wesentlichen darauf zurückzuführen, dass die Geschwindigkeit der Atome beziehungsweise Moleküle im Gas zunimmt. Dadurch beanspruchen die Teilchen mehr Raum, das Volumen des Gases nimmt zu. Experimentell lässt sich eine Ausdehnung bei konstantem Druck beispielsweise mittels eines (Luft-)Ballons in einem Wasserbad oder mittels eines Zylinders mit beweglichem Kolben verwirklichen. In beiden Fällen bleibt die Menge der Gasteilchen innerhalb des Gefäßes konstant, es handelt sich also um geschlossene Systeme.
Kann ein Gas während einer Temperaturänderung um  sein Volumen
sein Volumen
 nicht ändern, weil es beispielsweise in einem festen Behälter
eingesperrt ist, so ändert sich anstelle dessen sein Druck
nicht ändern, weil es beispielsweise in einem festen Behälter
eingesperrt ist, so ändert sich anstelle dessen sein Druck  .
.
Definition:
Bleibt das Volumen
während einer Temperaturänderung konstant, so ist die Druckänderung
eines Gases mit Druck
proportional zur Temperaturänderung
sowie zum (vom Stoff abhängigen) thermischen Volumenausdehnungskoeffizient
:
(6)¶
Die Zustandsgleichung eines idealen Gases
Unter Normaldruck und weit oberhalb des Siedepunkts verhalten sich alle Gase näherungsweise wie ein ideales Gas, d.h. das Volumen der einzelnen Gasteilchen kann (im Vergleich zum Gesamtvolumen) ebenso vernachlässigt werden wie die Wechselwirkung der einzelnen Teilchen untereinander.
Für das thermische Verhalten eines Gases sind neben der Temperatur 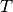 auch auch der Druck
auch auch der Druck  und das Volumen
und das Volumen  von Bedeutung.
von Bedeutung.
Formel:
Bleibt die Masse eines (idealen) Gases konstant, so ist das Produkt aus Druck
und Volumen
, geteilt durch die absolute Temperatur
, konstant:
(7)¶
Die Gleichung (7) wird als „Zustandsgleichung eines idealen Gases“ bezeichnet und gilt unter Normalbedingungen auch in sehr guter Näherung für reale Gase. Sie wird häufig auch in folgender Form geschrieben:
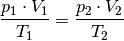
Dabei werden mit 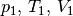 die thermischen Größen eines Gases
vor einer Zustandsänderung beschrieben, entsprechend stellen
die thermischen Größen eines Gases
vor einer Zustandsänderung beschrieben, entsprechend stellen 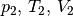 die thermischen Größen nach der Zustandsänderung dar. Bei
Kenntnis von fünf der sechs vorkommenden Größen kann somit jederzeit auch die
sechste Größe berechnet werden.
die thermischen Größen nach der Zustandsänderung dar. Bei
Kenntnis von fünf der sechs vorkommenden Größen kann somit jederzeit auch die
sechste Größe berechnet werden.
Beispiel:
Ein Gas mit einem Volumen von
![V_1 = \unit[50]{cm^3}](../_images/math/6a9637b0c30229e0069ff1461033602480bbad6a.png) , einem Druck von
, einem Druck von
![p_1 = \unit[2,5]{bar}](../_images/math/78a9814dc3b2759d4a0ddf5cf7697f149c435406.png) und einer Temperatur von
und einer Temperatur von ![T_1 =
\unit[0]{\degree C} \approx \unit[273]{K}](../_images/math/5e34ffff90bead24e13b427b878bf309dd7ef3cb.png) wird erwärmt. Dabei beträgt die
neue Temperatur
wird erwärmt. Dabei beträgt die
neue Temperatur ![T_2 = \unit[30]{\degree C} \approx \unit[303]{K}](../_images/math/6796fb9a82c197c07f24ba1a4919cc066ae9cf37.png) ,
gleichzeitig wird der Druck auf
,
gleichzeitig wird der Druck auf ![p_2 = \unit[6]{bar}](../_images/math/85735901cf9f3692b2f8e263fe71058164f733d3.png) erhöht. Mit Hilfe
der Zustandsgleichung für ideale Gase kann das neue Volumen
erhöht. Mit Hilfe
der Zustandsgleichung für ideale Gase kann das neue Volumen 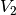 berechnet werden:
berechnet werden:![\frac{p_1 \cdot V_1 }{T_1 } = \frac{p_2 \cdot V_2 }{T_2 } \quad
\Leftrightarrow \quad V_2 = \frac{p_1 \cdot T_2 \cdot V_1 }{p_2 \cdot T_1}
\\[4pt]
V_2 = \frac{\unit[2,5]{bar} \cdot \unit[303]{K} \cdot \unit[50]{cm^3}
}{\unit[6]{bar} \cdot \unit[273]{K}} \approx \unit[23,12]{cm^3}](../_images/math/3b5417ff93dced64583516edd05f4b423c8b6b0e.png)
Das neue Luftvolumen
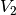 beträgt somit rund
beträgt somit rund
![\unit[23,12]{cm^3}](../_images/math/749f1890fb5bb6be4527c5ce1f1b0fba4c41196f.png) .
.
Aufgrund der vielen auftretenden Variablen ist die (allgemeine)
Zustandsgleichung eines idealen Gases (7)
etwas „unübersichtlich“. Anschaulicher wird die Bedeutung der Gleichung, wenn
man die drei möglichen Spezialfälle betrachtet, die sich ergeben, wenn jeweils
eine der Zustandsgrößen 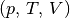 konstant
bleibt:
konstant
bleibt:
Wird das Volumen
 konstant gehalten („isochore“ Zustandsänderung), so
ist das Verhältnis aus Druck und Temperatur konstant:
konstant gehalten („isochore“ Zustandsänderung), so
ist das Verhältnis aus Druck und Temperatur konstant: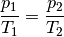
Wird beispielsweise die (absolute) Temperatur eines Gases bei gleich bleibendem Volumen verdoppelt, so verdoppelt sich auch der Druck im Gas.
Wird der Druck
 konstant gehalten („isobare“ Zustandsänderung[5]), so
ist das Verhältnis aus Volumen und Temperatur konstant:
konstant gehalten („isobare“ Zustandsänderung[5]), so
ist das Verhältnis aus Volumen und Temperatur konstant: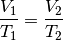
Wird die Temperatur eines Gases bei gleich bleibendem Druck erhöht, erhöht sich auch das Volumen und umgekehrt. Wird beispielsweise die Temperatur eines Gases verdoppelt, so verdoppelt sich auch sein Volumen.
Die Bestätigung dieses Zusammenhangs durch zahlreiche Experimente ist Grundlage der Festlegung der absoluten Temperatur auf
![\unit[-273,15]{\degree C} = \unit[0]{K}](../_images/math/0e67aa6066244e803e8e7cef4d2f98e856ce8f18.png) : Bei dieser Temperatur würde
ein ideales Gas kein Volumen mehr besitzen. Praktisch wird dieser „absolute
Nullpunkt“ nicht erreicht; reale Gase kondensieren vorher zu einer
Flüssigkeit.
: Bei dieser Temperatur würde
ein ideales Gas kein Volumen mehr besitzen. Praktisch wird dieser „absolute
Nullpunkt“ nicht erreicht; reale Gase kondensieren vorher zu einer
Flüssigkeit.
Wird die Temperatur
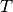 konstant gehalten („isotherme“ Zustandsänderung[6]), so ist bei Gasen das Produkt aus Druck und Volumen konstant:
konstant gehalten („isotherme“ Zustandsänderung[6]), so ist bei Gasen das Produkt aus Druck und Volumen konstant: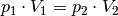
Wird das Volumen eines Gases bei gleich bleibender Temperatur verkleinert, erhöht sich der Druck und umgekehrt. Wird beispielsweise das Volumen eines Gases bei konstanter Temperatur halbiert, so verdoppelt sich der Druck.
Eine Erweiterung der Zustandsgleichung für ideale Gase stellt die allgemeine Gasgleichung dar.
Anmerkungen:
| [1] | Genau genommen stellen die Wärmeausdehnungs-Formeln „nur“ Näherungen dar; für die meisten Anwendungen sind sie allerdings völlig ausreichend. Siehe auch Wärmeausdehnung (Wikipedia) beziehungsweise Ausdehnungskoeffizient (Wikipedia) |
| [2] | Tatsächlich gibt es spezielle Festkörper-Kristalle, die in unterschiedlichen Raumrichtungen unterschiedliche physikalische Eigenschaften aufweisen. Die Untersuchung und Berechnung derartiger Besonderheiten ist ein Teilgebiet der Festkörperphysik. |
| [3] | Die Näherungsformel erhält man, wenn man den Term
Dadurch, dass die Werte von |
| [4] | Dies gilt genauso auch für Festkörper; da jedoch die Wärmeausdehnung bei Festkörpern wesentlich geringer ist als bei Flüssigkeiten, kann die temperaturbedingte Dichteänderung von Festkörpern meist vernachlässigt werden. |
| [5] | Der Zusammenhang 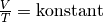 für für 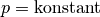 wird zu Ehren des Entdeckers Joseph Gay-Lussac auch als „Gesetz von
Gay-Lussac“ bezeichnet. wird zu Ehren des Entdeckers Joseph Gay-Lussac auch als „Gesetz von
Gay-Lussac“ bezeichnet. |
| [6] | Der Zusammenhang 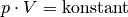 für für 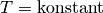 wird zu Ehren der Entdecker Robert Boyle und Edme Mariotte auch als „Gesetz von
Boyle-Mariotte“ bezeichnet. wird zu Ehren der Entdecker Robert Boyle und Edme Mariotte auch als „Gesetz von
Boyle-Mariotte“ bezeichnet. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

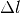 eines Festkörpers der Länge
eines Festkörpers der Länge  ist proportional zur Temperaturänderung
ist proportional zur Temperaturänderung  :
:![\Delta l = \alpha \cdot \Delta T \cdot l \\[6pt]](../_images/math/8a21d322c07e673c4edc28a271a1d945f5282244.png)
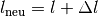 nach der
Temperaturänderung gilt damit:
nach der
Temperaturänderung gilt damit: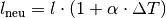
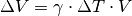
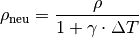
![\gamma_{\mathrm{Gas}} = \frac{1}{\unit[273,15]{K}} \approx 3,66 \cdot 10
^{-3} \frac{1}{K}](../_images/math/bd2a1f8c5ed574aaeb418953321d7b9b2f27a00a.png)
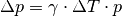
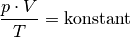
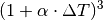 ausmultipliziert:
ausmultipliziert: