Die allgemeine Gasgleichung¶
Die Zustandsgleichung für ideale Gase in einem geschlossenen System kann auch in folgender Form geschrieben werden:
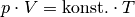
Betrachtet man ![\unit[1]{mol}](../_images/math/9d5ba3a89e8b1e69e55ba42b9681018af33bf44f.png) eines Gases, so ist der konstante Faktor
auf der rechten Seite der obigen Gleichung gleich der allgemeinen Gaskonstante
eines Gases, so ist der konstante Faktor
auf der rechten Seite der obigen Gleichung gleich der allgemeinen Gaskonstante
![R = \unit[8,31]{\frac{J}{mol \cdot K}}](../_images/math/190f89aec48e398d725cdd8af7351f1b57300a39.png) ; betrachtet man
; betrachtet man
![\unit[n]{mol}](../_images/math/41511a91a3e362ad0ecc12f4733082d9d04efb40.png) an Teilchen, so ist die Konstante entsprechend
an Teilchen, so ist die Konstante entsprechend
 -mal so groß. Es gilt somit für beliebige Gasmengen innerhalb eines
geschlossenen Systems:
-mal so groß. Es gilt somit für beliebige Gasmengen innerhalb eines
geschlossenen Systems:
(1)¶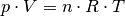
Diese Gleichung wird als „allgemeine Gasgleichung“ bezeichnet und gilt in sehr guter Näherung bei nicht allzu hohen Drücken auch für reale Gase.
Normalvolumen eines Gases:
Mit der Gleichung (1) kann beispielsweise bestimmt
werden, welches Volumen 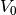 die Stoffmenge
die Stoffmenge ![n=\unit[1]{mol}](../_images/math/8025fd2aa20733bea574f1177f5ad99ab7bc6ba3.png) eines
idealen Gases unter Normalbedingungen, also bei einem Druck von
eines
idealen Gases unter Normalbedingungen, also bei einem Druck von
![p=\unit[101,3]{kPa}](../_images/math/a61eadc3cccf62be2d2ed7bfcf1e1f827303fe08.png) und einer Temperatur von
und einer Temperatur von ![T=\unit[273,15]{K}](../_images/math/bb13e2cf38ec198534026f1bbb848b7795bb71b0.png) einnimmt:
einnimmt:
![V_0 = \frac{\unit[1]{mol} \cdot \unit[8,31]{\frac{J}{mol \cdot K}} \cdot
\unit[273]{K}}{\unit[101,3 \cdot 10^3]{Pa}} \approx \unit[0,0224]{\frac{N
\cdot m}{\frac{N}{m^2}}} = \unit[0,0224]{m^3} = \unit[22,4]{l}](../_images/math/7930d204ab4965e52cf59589b6d58af27329a211.png)
Bei der obigen Rechnung wurde die Einheit Joule als Newton mal Meter und die
Einheit Pascal als Newton je Quadratmeter geschrieben. Als Ergebnis erhält man
fest, dass ein Mol eines idealen Gases (und in guter Näherung auch ein Mol
eines realen Gases) unter Normalbedingungen ein Volumen von rund
![\unit[22,4]{Litern}](../_images/math/3feaba9589e2989468cdd44f74c64eaafea4a11c.png) einnimmt.
einnimmt.
Teilchenzahl und molare Masse
Die allgemeine Gasgleichung stellt nicht nur einen Zusammenhang zwischen den
drei Zustandsgrößen Druck, Volumen und Temperatur her, sondern gibt
zusätzlich auch noch eine Beziehung zur Teilchenanzahl an. Da eine Stoffmenge
von ![n=\unit[1]{mol}](../_images/math/8025fd2aa20733bea574f1177f5ad99ab7bc6ba3.png) einer Anzahl von
einer Anzahl von ![N_{\mathrm{A}} =
\unit[6,022\cdot 10^{23}]{Teilchen}](../_images/math/3cf2675ced85b3faded4f85d55af233460044e79.png) entspricht („Avogadro-Konstante“), folgt
als weiterer Zusammenhang zwischen Stoffmenge
entspricht („Avogadro-Konstante“), folgt
als weiterer Zusammenhang zwischen Stoffmenge  und Teilchenzahl
und Teilchenzahl
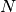 :
:
(2)¶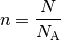
In einer Stoffmenge von ![\unit[n]{mol}](../_images/math/41511a91a3e362ad0ecc12f4733082d9d04efb40.png) eines Gases sind also
eines Gases sind also 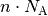 Teilchen enthalten. Die Stoffmenge
Teilchen enthalten. Die Stoffmenge  lässt sich
wiederum bestimmen, wenn man die Masse
lässt sich
wiederum bestimmen, wenn man die Masse  eines Gases und seine molare
Masse
eines Gases und seine molare
Masse 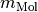 kennt:
kennt:
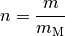
Die molare Masse 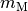 eines Gases kann anhand der relativen
Atommasse
eines Gases kann anhand der relativen
Atommasse 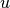 eines Elements aus einem Periodensystem der Elemente abgelesen werden. Bei Edelgasen, deren
Teilchen aus einzelnen Atomen bestehen, ist die molare Masse mit der relativen
Atommasse identisch. Bei Gasen wie Sauerstoff
eines Elements aus einem Periodensystem der Elemente abgelesen werden. Bei Edelgasen, deren
Teilchen aus einzelnen Atomen bestehen, ist die molare Masse mit der relativen
Atommasse identisch. Bei Gasen wie Sauerstoff 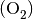 oder Stickstoff
oder Stickstoff
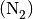 , deren Teilchen aus zwei-atomigen Molekülen bestehen,
entspricht die molare Masse der doppelten relativen Atommasse des Elements.
, deren Teilchen aus zwei-atomigen Molekülen bestehen,
entspricht die molare Masse der doppelten relativen Atommasse des Elements.
Beispiele:
Wie groß ist die molare Masse
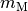 von Helium
von Helium
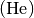 , Stickstoff
, Stickstoff 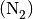 , Sauerstoff
, Sauerstoff 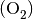 und Argon
und Argon 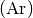 ?
?Helium hat eine relative Atommasse von
![\unit[4]{\frac{g}{mol}}](../_images/math/de5ccee632ad4f3a9193e40c2fca66eade2669dc.png) . Da
Helium-Atome als einzelne Atome in Heliumgas auftreten, gilt auch für die
molare Masse von Helium:
. Da
Helium-Atome als einzelne Atome in Heliumgas auftreten, gilt auch für die
molare Masse von Helium:![m_{\mathrm{M,Helium}} = \unit[4]{\frac{g}{mol}}](../_images/math/b9e49451ca84d68dbf19c08d8b1c2a570682524c.png)
Stickstoff hat eine relative Atommasse von
![\unit[14]{\frac{g}{mol}}](../_images/math/4ad943ef7532d0cddcf6e19b625b6bb2ea6d441a.png) ,
Sauerstoff eine relative Atommasse von
,
Sauerstoff eine relative Atommasse von ![\unit[16]{\frac{g}{mol}}](../_images/math/90ffb4b7e7141d357f2ced5e2274c8a2c6d74de6.png) .
Sowohl Stickstoff wie auch Sauerstoff treten als zweiatomige Moleküle auf.
Die molare Masse dieser Gase ist somit doppelt so gross wie die relative
Atommasse der Elemente:
.
Sowohl Stickstoff wie auch Sauerstoff treten als zweiatomige Moleküle auf.
Die molare Masse dieser Gase ist somit doppelt so gross wie die relative
Atommasse der Elemente:![m_{\mathrm{M,Stickstoff}} &= 2 \cdot \unit[14]{\frac{g}{mol}}=
\unit[28]{\frac{g}{mol}} \\
m_{\mathrm{M,Sauerstoff}} &= 2 \cdot \unit[16]{\frac{g}{mol}}=
\unit[32]{\frac{g}{mol}} \\](../_images/math/7377209c20593c5c4bb902f9436631d9d33cf21d.png)
Argon hat eine relative Atommasse von
![\unit[40]{\frac{g}{mol}}](../_images/math/921d702142217f244c894de02be49f3f257914fb.png) . Da
Argon ebenso wie Helium als ein-atomiges Gas auftritt, gilt für die molare
Masse von Argon:
. Da
Argon ebenso wie Helium als ein-atomiges Gas auftritt, gilt für die molare
Masse von Argon:![m_{\mathrm{M,Argon}} = \unit[40]{\frac{g}{mol}}](../_images/math/4854b15caac47485f1f0c8045d3460094bf737b5.png)
Wie groß ist die molare Masse von Luft?
Luft besteht näherungsweise aus
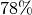 Stickstoff,
Stickstoff, 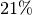 Sauerstoff und
Sauerstoff und 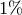 Argon. Die molare Masse von Luft entspricht der
durchschnittlichen molaren Masse ihrer Bestandteile, wobei die
unterschiedlichen Mengenverhältnisse als Gewichtungsfaktoren berücksichtigt
werden:
Argon. Die molare Masse von Luft entspricht der
durchschnittlichen molaren Masse ihrer Bestandteile, wobei die
unterschiedlichen Mengenverhältnisse als Gewichtungsfaktoren berücksichtigt
werden:![m_{\mathrm{M, Luft}} = 0,78 \cdot \unit[28]{\frac{g}{mol}} + 0,21 \cdot
\unit[32]{\frac{g}{mol}} + 0,01 \cdot \unit[40]{\frac{g}{mol}} \approx
\unit[29]{\frac{g}{mol}}](../_images/math/eba0f17c419bd5a3f548d9b7e5526546efd82668.png)
Anhand der molaren Masse eines Gases kann mittels der allgemeinen Gasgleichung beispielsweise dessen Dichte bei einem bestimmten Druck und einer bestimmten Temperatur bestimmt werden:
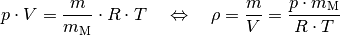
Für Luft gilt beispielsweise unter Normalbedingungen, also bei ![p =
\unit[101,3]{kPa}](../_images/math/6fedcf78d79d59a2e89ed00b6df8bf2197423206.png) und
und ![T = \unit[273]{K}](../_images/math/6c15eb7e1a57666cfce56c59e2c35cfd5c2e41c9.png) :
:
![\rho_{\mathrm{Luft}} = \frac{\unit[101,3 \cdot 10^3]{Pa} \cdot
\unit[29]{\frac{g}{mol}}}{\unit[8,31]{\frac{J}{mol \cdot K}} \cdot
\unit[273]{K}} \approx \unit[1294,9]{\frac{\frac{N}{m^2} \cdot g}{N \cdot
m}} = \unit[1294,9]{\frac{ g}{m^3}} \approx \unit[1,29]{\frac{kg}{m^3}}](../_images/math/fe855d49bd2b37adcae83cc589b9c2dc20a8d044.png)
Hierbei wurde für die Einheit Pascal durch Newton je Quadratmeter und die Einheit Joule durch Newton mal Meter ersetzt. Der so berechnete Dichte-Wert von Luft stimmt mit experimentellen Messungen sehr gut überein.
Gasgemische und Partialdrücke¶
Bei Gasgemischen, wie beispielsweise Luft, kann die allgemeine Gasgleichung für jede einzelne Komponente aufgeschrieben werden:
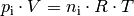
In dieser Gleichung gibt 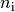 die Stoffmenge der
die Stoffmenge der 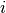 -ten
Komponente an. Die zu Grunde liegende Idee hierbei ist wiederum, dass sich die
Gasteilchen nicht gegenseitig beeinflussen, die gleiche Temperatur haben sowie
das gleiche Volumen einnehmen. Man kann die obige Gleichung auch so deuten, dass
jede der
-ten
Komponente an. Die zu Grunde liegende Idee hierbei ist wiederum, dass sich die
Gasteilchen nicht gegenseitig beeinflussen, die gleiche Temperatur haben sowie
das gleiche Volumen einnehmen. Man kann die obige Gleichung auch so deuten, dass
jede der 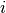 Komponenten zu einem eigenen „Partialdruck“
Komponenten zu einem eigenen „Partialdruck“
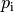 führt:
führt:
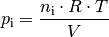
Der Gesamtdruck eines Gasgemisches ist dann die Summe aller Partialdrücke der einzelnen Komponenten. Dieses Prinzip wird nach ihrem Entdecker auch als Gesetz von Dalton bezeichnet:
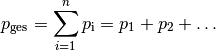
Luft besteht beispielsweise zu 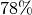 aus Stickstoff
aus Stickstoff 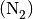 , zu
, zu
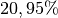 aus Sauerstoff
aus Sauerstoff 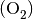 und zu
und zu 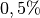 aus
anderen Gasen (z.B. Argon und Kohlenstoffdioxid). Die Partialdrücke der
einzelnen Gase entsprechen den Mol-Anteilen
aus
anderen Gasen (z.B. Argon und Kohlenstoffdioxid). Die Partialdrücke der
einzelnen Gase entsprechen den Mol-Anteilen 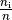 der
einzelnen Substanzen. Bei einem Normal-Luftdruck von
der
einzelnen Substanzen. Bei einem Normal-Luftdruck von ![\unit[1,01]{bar}](../_images/math/30d6c589bdad49c4106d5eb2e671be342e92ccb4.png) ergibt sich folglich ein Partialdruck von
ergibt sich folglich ein Partialdruck von ![\unit[0,78]{bar}](../_images/math/3b4a0015e7011db4d60ab952dae6451ae35aa596.png) für
Stickstoff, ein Partialdruck von
für
Stickstoff, ein Partialdruck von ![\unit[0,2095]{bar}](../_images/math/c753450440b61d5563d2eca7d3db17fc47149c80.png) für Sauerstoff usw.
für Sauerstoff usw.
Luft kann zudem Wasserdampf aufnehmen, die dem Sättigungs-Dampfdruck von Wasser
entspricht – dieser ist temperaturabhängig und beträgt bei
![\unit[20]{\degree}](../_images/math/38e102f67191b7607a7b62a3bf6e37a0897d2bb8.png) etwa
etwa ![\unit[0,023]{bar}](../_images/math/0bb33a1fbef97fa8d9cf896b0e200fcadf25ddc3.png) .
.
Die Van-der-Waals-Gleichung¶
Die allgemeine Gasgleichung (1) gilt in guter
Näherung nur für Gase mit geringer Dichte. Bei großen Gasdichten, beispielsweise
bei gesättigtem Dampf, können reale Gase nicht mehr als „ideale“ Gase betrachtet
werden. In diesem Fall muss einerseits die Wechselwirkung zwischen den
Gasmolekülen, andererseits auch das Eigenvolumen der Gasteilchen berücksichtigt
werden. Aus der allgemeinen Gasgleichung ergibt sich mit den entsprechenden
Korrektur-Termen die so genannte Van-der-Waals-Gleichung, die für  Mole
eines Gases folgendermaßen lautet:
Mole
eines Gases folgendermaßen lautet:
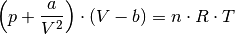
Hierbei bezeichnet 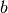 das Eigenvolumen der Gasteilchen; durch den
Korrekturterm
das Eigenvolumen der Gasteilchen; durch den
Korrekturterm 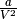 wird der durch die Wechselwirkungen der
Gasteilchen verursachte Binnendruck berücksichtigt.
wird der durch die Wechselwirkungen der
Gasteilchen verursachte Binnendruck berücksichtigt.
In einem 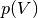 -Diagramm verlaufen die Isothermen oberhalb einer
bestimmten, als „kritisch“ bezeichneten Temperatur
-Diagramm verlaufen die Isothermen oberhalb einer
bestimmten, als „kritisch“ bezeichneten Temperatur 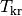 ebenso wie die Isothermen von idealen Gasen. Unterhalb von
ebenso wie die Isothermen von idealen Gasen. Unterhalb von
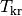 sind die Isothermen S-förmig gebogen.
sind die Isothermen S-förmig gebogen.
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.
