Wärmekapazität und Phasenübergänge¶
Wärme kann als eine Energieform aufgefasst werden. Führt man in einem isolierten
System einem Gegenstand eine Wärmemenge 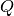 zu, so erhöht sich dessen
Temperatur
zu, so erhöht sich dessen
Temperatur 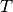 . Eine Voraussetzung dafür ist allerdings, dass sich der
Aggregatzustand des Gegenstands während der Wärmezufuhr nicht ändert, also kein
Phasenübergang (Schmelzen, Verdunsten, Sublimieren)
stattfindet.
. Eine Voraussetzung dafür ist allerdings, dass sich der
Aggregatzustand des Gegenstands während der Wärmezufuhr nicht ändert, also kein
Phasenübergang (Schmelzen, Verdunsten, Sublimieren)
stattfindet.
Wärmemenge und Wärmekapazität¶
Wie viel Wärme bei einem konkreten Gegenstand für eine bestimmte Erwärmung nötig
ist, hängt vom Material des Gegenstands und seiner Masse ab: Eine Tasse Wasser
benötigt für eine gleiche Erwärmung wesentlich weniger Energie als ein ganzes
Schwimmbad. Die Menge an Wärme, die man einem konkreten Gegenstand der Masse
 zuführen muss, um ihn um
zuführen muss, um ihn um ![\Delta T = \unit[1]{K}](../_images/math/9e11c4e214ba50309e6b8ecb705dcf9fb7e76c5c.png) zu erwärmen,
wird als Wärmekapazität
zu erwärmen,
wird als Wärmekapazität 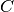 des Gegenstands bezeichnet; ihre Einheit ist
des Gegenstands bezeichnet; ihre Einheit ist
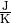 . Für die zur Erwärmung nötige Wärmemenge
. Für die zur Erwärmung nötige Wärmemenge 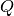 gilt:
gilt:
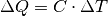
Die spezifische Wärmekapazität
Um Gegenstände aus unterschiedlichen Materialien hinsichtlich ihrer Wärmekapazität vergleichen zu können, gibt man die materialspezifische Wärmekapazität üblicherweise bezogen auf ein Kilogramm des jeweiligen Materials an.
Definition:
Die Menge
an Wärme, die nötig ist, um
eines Stoffes um
zu erwärmen, wird als spezifischen Wärmekapazität
bezeichnet:
(1)¶
Die Einheit der spezifischen Wärmekapazität ist gemäß der obigen Formel
.
Beispiele:
- Um
![m = \unit[1]{kg}](../_images/math/a7f7cea70acf83856cbc0f17330ebc12d88f4937.png) Wasser um
Wasser um ![\Delta T = \unit[1]{K}](../_images/math/9e11c4e214ba50309e6b8ecb705dcf9fb7e76c5c.png) zu
erwärmen, sind
zu
erwärmen, sind ![\Delta Q = \unit[4182]{J} \approx \unit[4,2]{kJ}](../_images/math/082a6253b7e5faf0032944619b2a97b25d4f6ab0.png) an
Wärme nötig.
an
Wärme nötig. - Eisen benötigt je Kilogramm nur
![\Delta Q = \unit[452]{J} \approx
\unit[0,45]{kJ}](../_images/math/6885a0ed1dbe5c955d8558abbc4ca444e5386b03.png) , um eine Erwärmung von einem Kelvin zu bewirken. Es hat damit
(wie alle bekannten Stoffe) eine deutlich kleinere spezifische Wärmekapazität
als Wasser.
, um eine Erwärmung von einem Kelvin zu bewirken. Es hat damit
(wie alle bekannten Stoffe) eine deutlich kleinere spezifische Wärmekapazität
als Wasser.
| Stoff | Wärmekapazität  in in ![\unit[]{\frac{kJ}{kg}}](../_images/math/b82843e0ffdc68d2f8fffd63599d413fbebb8ea1.png) |
| Aluminium | 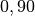 |
| Blei | 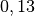 |
| Eis | 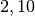 |
| Eisen | 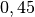 |
| Ethanol | 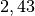 |
| Holz (trocken) | 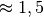 |
| Kupfer | 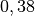 |
| Petroleum | 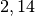 |
| Quecksilber | 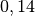 |
| Silber | 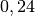 |
| Wasser | 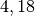 |
| Wolfram | 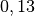 |
| Zinn | 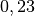 |
Spezifische Wärmekapazität bei Gasen
Bei Gasen hängt die spezifische Wärmekapazität von der Art der Erwärmung ab.
Je nachdem, ob während der Erwärmung der Druck  oder das Volumen
oder das Volumen
 konstant gehalten wird, unterscheidet man zwischen den
Wärmekapazitäten
konstant gehalten wird, unterscheidet man zwischen den
Wärmekapazitäten 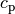 und
und 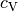 :
:
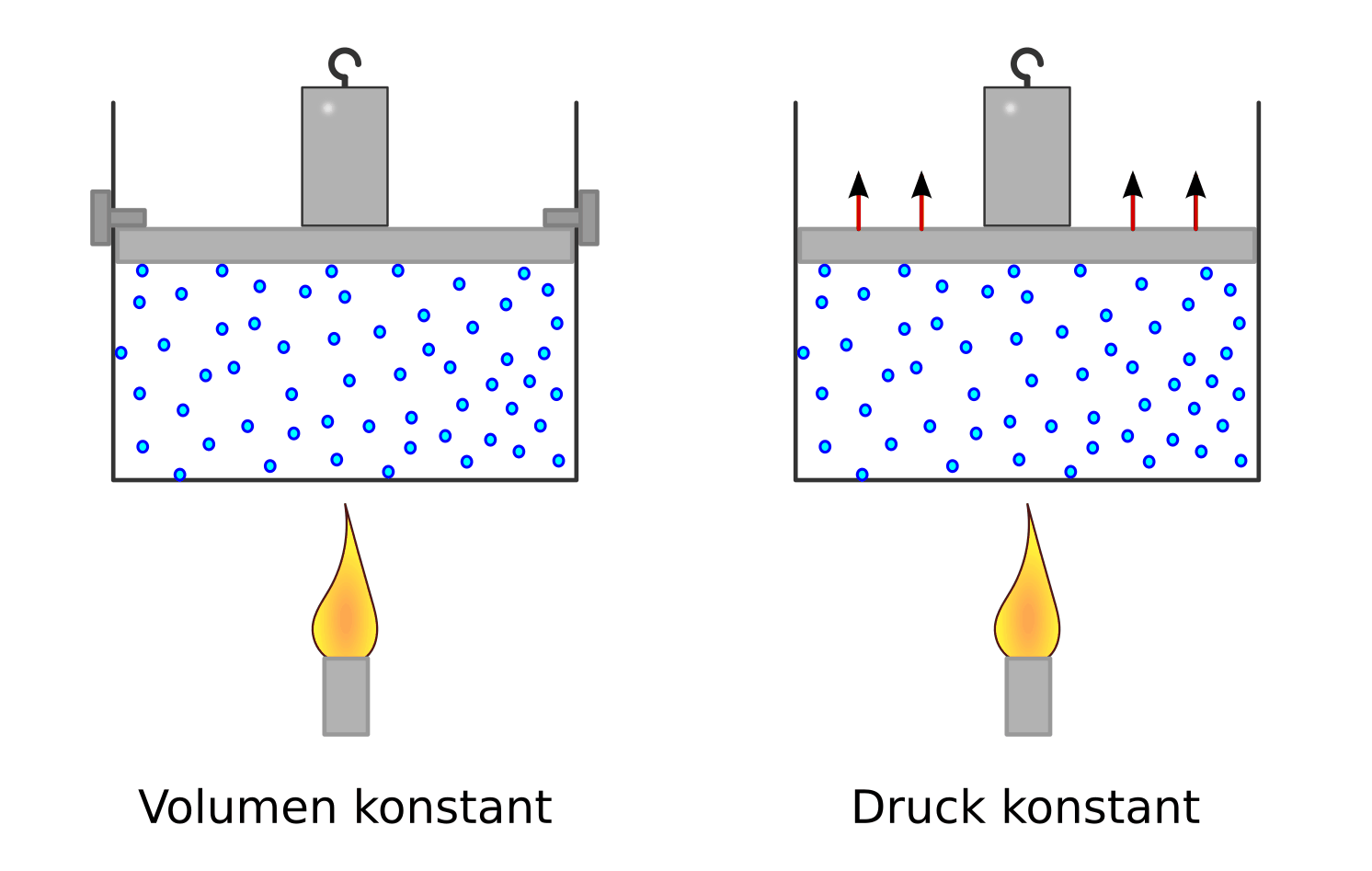
- Die spezifische Wärmekapazität
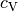 eines Gases gibt an,
wie viel Energie zur Erwärmung eines Kilogramms um ein Grad nötig ist, wenn
das Volumen des Gases konstant bleibt. Die zugeführte Wärmemenge führt
ausschließlich zu einer Erhöhung der mittleren Energie der Moleküle.
eines Gases gibt an,
wie viel Energie zur Erwärmung eines Kilogramms um ein Grad nötig ist, wenn
das Volumen des Gases konstant bleibt. Die zugeführte Wärmemenge führt
ausschließlich zu einer Erhöhung der mittleren Energie der Moleküle. - Die spezifische Wärmekapazität
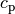 eines Gases gibt an, wie
viel Energie zur Erwärmung eines Kilogramms um
eines Gases gibt an, wie
viel Energie zur Erwärmung eines Kilogramms um ![\Delta T = \unit[1]{K}](../_images/math/9e11c4e214ba50309e6b8ecb705dcf9fb7e76c5c.png) nötig ist, wenn der Druck des Gases konstant bleibt. Die zugeführte Wärmemenge
erhöht hierbei einerseits die mittlere Energie der Moleküle, andererseits muss
auch eine so genannte „Ausdehnungsarbeit“ am Gas verrichtet werden.
nötig ist, wenn der Druck des Gases konstant bleibt. Die zugeführte Wärmemenge
erhöht hierbei einerseits die mittlere Energie der Moleküle, andererseits muss
auch eine so genannte „Ausdehnungsarbeit“ am Gas verrichtet werden.
Ein gute Modellvorstellung hierfür liefert ein kubischer Gasbehälter, der nach oben durch einen beweglichen Kolben abgeschlossen ist. Auf dem Kolben wird ein Gewicht angebracht, das den Kolben so weit nach innen drückt, bis durch die Kompression des Gases ein entsprechend großer Gegendruck entsteht. Der durch das Gewicht bewirkte Kolbendruck ist dann mit dem Gasdruck im Gleichgewicht.
Bei einer Erwärmung mit konstantem Volumen wird der Kolben bei dieser Anordnung nach oben hin mit zwei Bolzen fixiert, so dass sich das Gas auch bei zunehmender Temperatur nicht ausdehnen kann. Ohne Fixierung hingegen kann sich das Gas hingegen nach oben hin ausdehnen, bis sich wiederum ein Gleichgewicht zwischen dem Kolben- Gasdruck einstellt.
Dehnt sich das Gas bei konstantem Druck  um das Volumen
um das Volumen 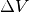 aus, so gilt für die vom Gas verrichtete Ausdehnungsarbeit:
aus, so gilt für die vom Gas verrichtete Ausdehnungsarbeit:
(2)¶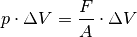
Hat der kubische Gasbehälter die Seitenlänge  , so gilt
, so gilt 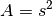 ,
und
,
und 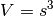 . Insgesamt ergibt sich also
. Insgesamt ergibt sich also 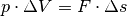 , was mit der Definition der Arbeit
übereinstimmt.
, was mit der Definition der Arbeit
übereinstimmt.
Allgemein gilt für beliebige Gase stets 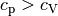 ,
da bei konstantem keine Energie für die Ausdehnung des Gases zugeführt werden
muss. Bei konstantem Druck steht der Anteil der zugeführten Energie, der zur
Verrichtung der Ausdehnungsarbeit benötigt wird, nicht für die Erwärmung des
Gases zur Verfügung, es muss also mehr Energie für eine gleiche Erwärmung
investiert werden.
,
da bei konstantem keine Energie für die Ausdehnung des Gases zugeführt werden
muss. Bei konstantem Druck steht der Anteil der zugeführten Energie, der zur
Verrichtung der Ausdehnungsarbeit benötigt wird, nicht für die Erwärmung des
Gases zur Verfügung, es muss also mehr Energie für eine gleiche Erwärmung
investiert werden.
Bei Flüssigkeiten ist die Wärmeausdehnung wesentlich geringer als
bei Gasen, so dass hierbei häufig nur ein  -Wert angegeben wird.
-Wert angegeben wird.
Mischungsvorgänge¶
Bei Mischungsvorgängen in einer isolierten Umgebung wird vom wärmeren Objekt genauso viel Wärme abgegeben, wie vom kälteren Objekt aufgenommen wird. Dies gilt für Festkörper, Flüssigkeiten und Gase gleichermaßen. Dieser Sonderfall des Energieerhaltungssatzes wird auch Richmannsche Mischungsregel bezeichnet:
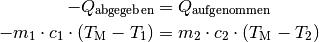
Mit 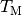 wird die Mischungstemperatur bezeichnet, die sich
nach dem Mischungsvorgang ergibt. Die Vorzeichen der Wärmebilanz ergeben sich
daraus, dass aufgenommene Wärmemengen der Konvention nach positiv gezählt,
abgegebene Wärmemengen hingegen negativ gewertet werden. Auf beiden Seiten
wurden in der obigen Gleichung die Wärmemengen dann mittels der Formel
(1) für die spezifische Wärmekapazität
ausgedrückt. Die linke Seite der Gleichung kann etwas umgestellt werden, indem
das Minus-Zeichen in die Klammer übernommen wird:
wird die Mischungstemperatur bezeichnet, die sich
nach dem Mischungsvorgang ergibt. Die Vorzeichen der Wärmebilanz ergeben sich
daraus, dass aufgenommene Wärmemengen der Konvention nach positiv gezählt,
abgegebene Wärmemengen hingegen negativ gewertet werden. Auf beiden Seiten
wurden in der obigen Gleichung die Wärmemengen dann mittels der Formel
(1) für die spezifische Wärmekapazität
ausgedrückt. Die linke Seite der Gleichung kann etwas umgestellt werden, indem
das Minus-Zeichen in die Klammer übernommen wird:
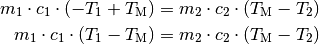
Diese Gleichung kann nach der gesuchten Größe 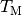 aufgelöst
werden. Dazu werden beide Seiten der Gleichung ausmultipliziert und anschließend
sortiert:
aufgelöst
werden. Dazu werden beide Seiten der Gleichung ausmultipliziert und anschließend
sortiert:
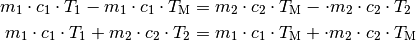
Auf der rechten Seite der Gleichung kann 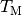 ausgeklammert
werden; für die Mischtemperatur ergibt sich damit folgende Formel:
ausgeklammert
werden; für die Mischtemperatur ergibt sich damit folgende Formel:
(3)¶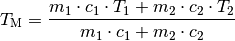
Haben die Wärme austauschenden Objekte eine gleiche Wärmekapazität, so kann diese im Zähler sowie im Nenner ausgeklammert und gekürzt werden. Damit vereinfacht sich die Formel folgendermaßen:
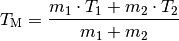
Man kann an dieser Formel erkennen, dass bei gleichen Wärmekapazitäten die
Massenanteile 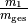 und
und
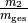 Gewichtungsfaktoren für die Mischtemperatur
sind: Eine große Masse von
Gewichtungsfaktoren für die Mischtemperatur
sind: Eine große Masse von 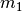 (im Vergleich zu
(im Vergleich zu 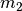 ) führt zu
einer Verschiebung der Mischtemperatur in Richtung von
) führt zu
einer Verschiebung der Mischtemperatur in Richtung von 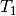 . Sind die
Wärmekapazitäten der gemischten Substanzen verschieden, so treten diese
zusätzlich als Gewichtungsfaktoren auf.
. Sind die
Wärmekapazitäten der gemischten Substanzen verschieden, so treten diese
zusätzlich als Gewichtungsfaktoren auf.
Sind mehr als zwei Gegenstände beziehungsweise Substanzen am Mischungsvorgang beteiligt, so müssen die dabei umgesetzten Wärmemengen ebenfalls berücksichtigt werden. Allgemein gilt somit:
(4)¶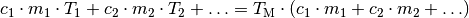
Mittels der obigen Formeln kann experimentell wahlweise die spezifische Wärmekapazität eines Gegenstands oder seine Anfangstemperatur bestimmt werden. Isolierte Anordnungen, die zu genau diesem Zweck konstruiert sind, heißen Kalorimeter.
Phasenübergänge¶
In welchem Zustand ein Stoff vorliegt, hängt von seiner Temperatur und dem Druck seiner Umgebung ab. Je nachdem, wie groß die thermische Bewegungsenergie der einzelnen Teilchen gegenüber der Stärke ihrer Bindungen mit den Nachbarteilchen ist, können (fast) alle Stoffe als fest, flüssig oder gasförmig vorkommen.[1]
Wechsel zwischen den drei Aggregatzuständen fest, flüssig und gasförmig werden als Phasenübergange bezeichnet.
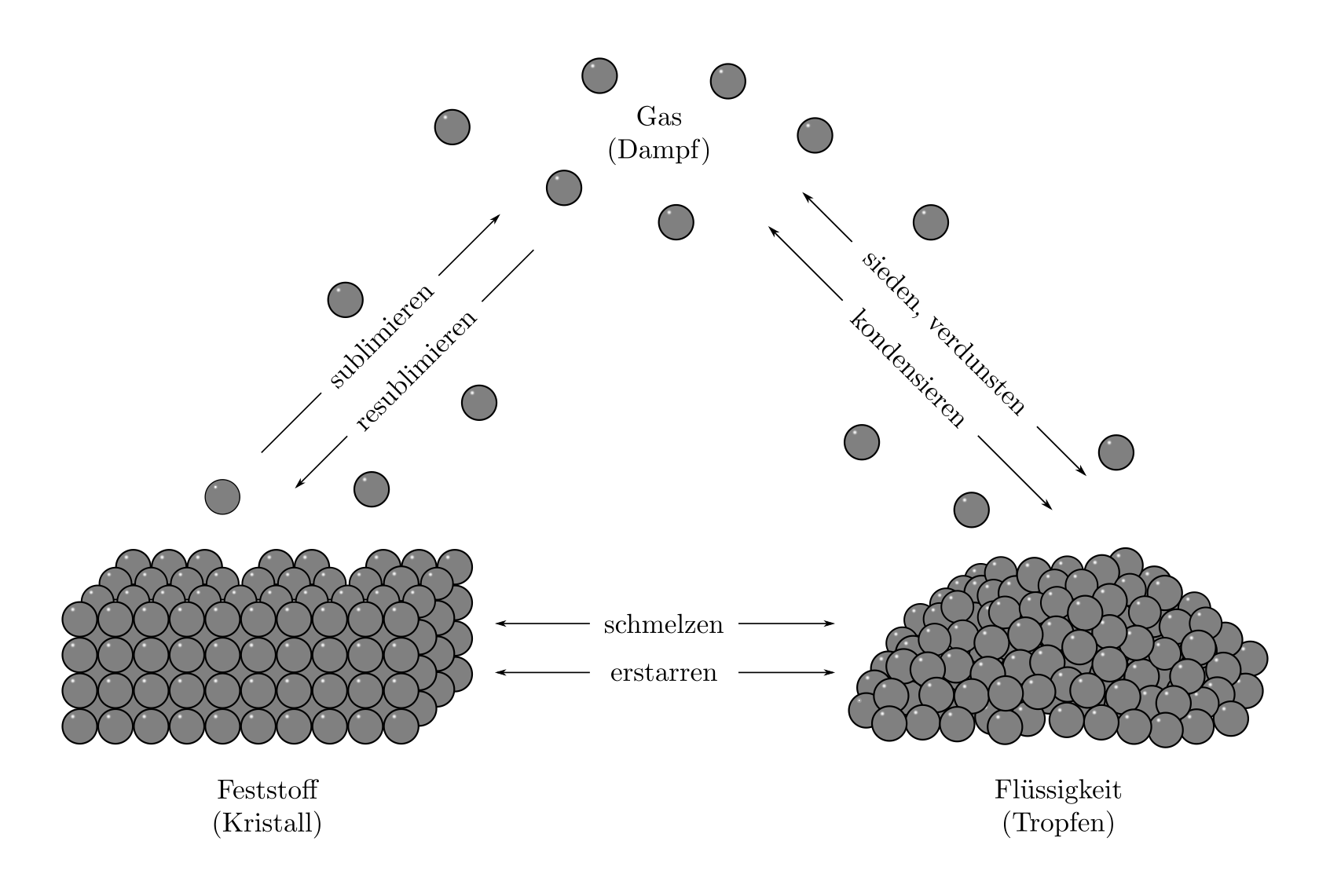
Teilchenmodell von Festkörpern, Flüssigkeiten, und Gasen sowie Phasenübergänge zwischen den drei Aggregatzuständen.
Schmelzen und Erstarren¶
Wird ein Festkörper erwärmt, so schwingen seine Teilchen immer stärker um ihre Ruhelage. Zu einem bestimmten Zeitpunkt reichen die im Objekt wirkenden Kohäsionskräfte nicht mehr aus, um die Teilchen an ihre Plätze zu binden – der Festkörper schmilzt.
Wird einer Flüssigkeit Wärme entzogen, so geht sie bei einer bestimmten Temperatur wieder in den festen Aggregatzustand über. Dieser Vorgang heißt Erstarren.
Grundsätzlich gilt für beliebige Schmelz- und Erstarrungsvorgänge:
- Wärme, die einem Festkörper während des Schmelzens zugeführt wird, ist zum Aufbrechen der Festkörper-Strukturen nötig und steht somit nicht für eine Temperaturerhöhung zur Verfügung. Die Temperatur bleibt während des Schmelzvorgangs stets konstant.
- Die Schmelz- und Erstarrungstemperatur eines Stoffes sind identisch. Ebenso sind die zum Schmelzen nötige beziehungsweise die beim Erstarren frei werdenden Wärmemengen (Schmelzenergie beziehungsweise Erstarrungsenergie) identisch.
Die meisten Materialien dehnen sich beim Schmelzen aus und ziehen sich beim Erstarren zusammen (Ausnahme: Die Anomalie des Wassers).
| Stoff | Schmelztemperatur in 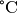 |
| Aluminium | 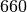 |
| Blei | 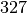 |
| Eis | 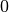 |
| Eisen | 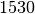 |
| Kupfer | 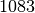 |
| Quecksilber | 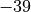 |
| Silber | 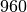 |
| Wolfram | 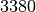 |
| Zinn | 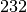 |
Manche Stoffe, beispielsweise Glas, haben keine bestimmte Schmelztemperatur:
- Glas erweicht bei
![\unit[700]{\degree C}](../_images/math/06a15d1bdddeafdf9c936705130510eebefbe14e.png) und wird bei
und wird bei
![\unit[1\,300]{\degree C}](../_images/math/cd885524cb393410123fafbaeb5e3acac24fe628.png) dünnflüssig. Man kann Glas als eine
Flüssigkeit ansehen, die bei Zimmertemperatur äußerst zäh ist.[2]
dünnflüssig. Man kann Glas als eine
Flüssigkeit ansehen, die bei Zimmertemperatur äußerst zäh ist.[2] - Andere Stoffe, beispielsweise Holz, verbrennen, wenn man sie an Luft stark erwärmt.
Die Schmelzwärme
Um einen bestimmten Feststoff zum Schmelzen zu bringen, muss ihm eine entsprechende Wärmemenge zugeführt werden. Die Menge an Wärme ist von der Art des Stoffs und seiner Masse abhängig.
Definition:
Die spezifische Schmelzwärme
eines Materials gibt an, welche Wärmemenge
nötig ist, um ein Kilogramm des Stoffes bei seiner Schmelztemperatur zu schmelzen:
Die spezifische Schmelzwärme wird üblicherweise in ![\unit[kJ]{kg}](../_images/math/09f2a94251ff4eafb398d2ddb71d4d9bdcb0efcd.png) angegeben. Beim Erstarren wird die gleiche Menge an Wärme wieder an die Umgebung
abgegeben.
angegeben. Beim Erstarren wird die gleiche Menge an Wärme wieder an die Umgebung
abgegeben.
| Stoff | Schmelzwärme 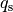 in in 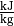 |
| Aluminium | 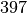 |
| Blei | 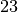 |
| Eis | 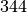 |
| Eisen | 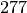 |
| Kupfer | 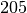 |
| Quecksilber | 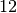 |
| Silber | 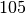 |
| Wolfram | 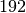 |
| Zinn | 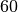 |
Sieden und Kondensieren¶
Wird ein flüssiger Stoff auf seine Siedetemperatur erhitzt, so bewegen sich die Flüssigkeitsteilchen mit sehr großer Geschwindigkeit. Sie können dadurch die Kohäsionskräfte überwinden. Innerhalb der Flüssigkeit entstehen Dampfblasen, der Stoff geht in den gasförmigen Aggregatzustand über. Dabei muss Wärme zugeführt werden.
Wird Dampf Wärme entzogen, so geht er bei einer bestimmten Temperatur wieder in den flüssigen Aggregatzustand über. Dieser Vorgang heißt Kondensieren.
- Während des Siedens ändert sich die Temperatur des Materials trotz Wärmezufuhr nicht.
- Die Siedetemperatur und Kondensationstemperatur eines Stoffes sind identisch.
| Stoff | Siedetemperatur in 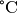 |
| Aluminium | 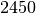 |
| Blei | 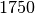 |
| Eisen | 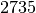 |
| Ethanol | 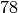 |
| Kupfer | 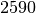 |
| Meerwasser | 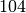 |
| Quecksilber | 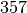 |
| Silber | 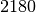 |
| Wasser | 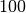 |
| Wolfram | 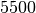 |
| Zinn | 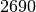 |
Die Verdampfungswärme
Um eine bestimmte Flüssigkeit zum Sieden zu bringen, muss ihr – ebenso wie beim Schmelzen – eine entsprechende Wärmemenge zugeführt werden. Die Menge an Wärme ist wiederum von der Art der Flüssigkeit und ihrer Masse abhängig.
Definition:
Die spezifische Verdampfungswärme
einer Flüssigkeit gibt an, welche Wärmemenge
nötig ist, um ein Kilogramm der Flüssigkeit bei ihrer Siedetemperatur zu verdampfen:
Beim Kondensieren wird die gleiche Menge an Wärme wieder an die Umgebung abgegeben.
| Stoff | Verdampfungswärme 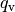 in in
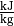 |
| Aluminium | 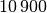 |
| Benzol | 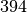 |
| Blei | 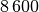 |
| Eisen | 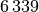 |
| Ethanol | 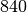 |
| Kupfer | 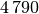 |
| Quecksilber | 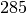 |
| Silber | 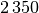 |
| Wasser | 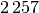 |
| Wolfram | 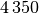 |
| Zinn | 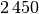 |
Geht bei Sublimations- beziehungsweise Resublimationsvorgängen ein Stoff unmittelbar von der festen in die gasförmige Phase über (oder umgekehrt), so ist die spezifische Wärme gleich der Summe der Schmelz- und Verdampfungswärme des jeweiligen Stoffs.
Anhand der Werte aus den Tabellen zur Schmelz- und Verdampfungswärme erkennt man, dass für die Phasenübergänge große Mengen an Wärme zugeführt werden müssen. Da sich die Temperatur während des Schmelzens und Siedens nicht ändert, nennt man die bei Phasenübergängen umgesetzte Wärmemenge auch „latente Wärme“.
Verdunsten¶
Flüssigkeiten können bereits unterhalb ihrer Siedetemperatur in den gasförmigen Aggregatzustand übergehen. Beim Verdunsten müssen die Flüssigkeitsteilchen an der Oberfläche die Kohäsionskräfte der anderen Teilchen überwinden. Das ist möglich, weil sich nicht alle Flüssigkeitsteilchen mit der gleichen Geschwindigkeit bewegen. Nur Teilchen mit großer Geschwindigkeit sind in der Lage, die Flüssigkeit zu verlassen, wenn sie an die Oberfläche gelangen.
Die in der Flüssigkeit verbleibenden Teilchen haben eine geringere durchschnittliche Geschwindigkeit als die verdunstenden; somit entschwindet beim Verdunsten mit den schnellen, aus der Flüssigkeit entweichenden Teilchen auch Wärme. Die verbleibende Flüssigkeit kühlt sich daher ab („Verdunstungskälte“).[3]
Das Verdunsten einer Flüssigkeit kann folgendermaßen beeinflusst werden:
- Je höher die Temperatur und je größer die Oberfläche, desto schneller verdunstet eine Flüssigkeit.
- Wird der entstehende Dampf fortgeführt, so verdunstet die Flüssigkeit ebenfalls schneller.
Ebenfalls relevant für den Verdunstungsvorgang ist die Dampfmenge in der umgebenden Luft; im Fall von Wasserdampf spricht man von Luftfeuchtigkeit.
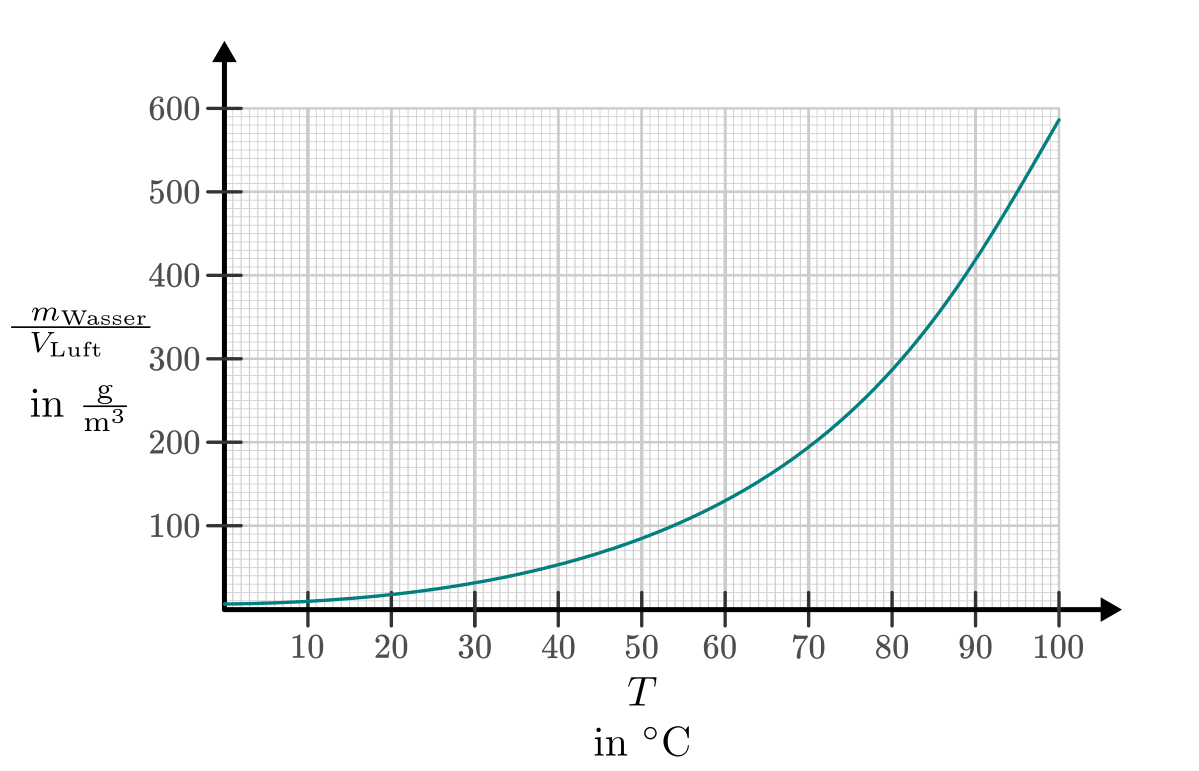
Die Menge an Wasserdampf, die ein bestimmtes Volumen an Luft maximal aufnehmen kann, ist stark abhängig von der Temperatur der Luft. Wie man an den Werten aus der obigen Tabelle beziehungsweise am folgenden Diagramm sehen kann, nimmt diese so genannte „Sättigungsmenge“ mit der Temperatur überproportional zu.
Temperatur in 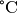 |
Sättigungsmgenge (Wasser) in 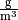 |
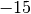 |
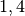 |
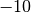 |
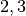 |
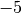 |
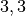 |
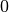 |
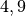 |
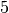 |
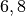 |
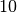 |
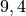 |
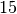 |
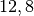 |
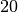 |
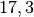 |
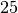 |
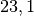 |
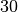 |
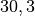 |
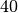 |
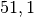 |
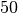 |
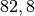 |
Die „absolute“ Feuchtigkeit von Luft gibt an, wie viel Gramm Wasserdampf aktuell
je Kubikmeter enthalten sind; die „relative“ Luftfeuchtigkeit hingegen gibt
diesen Wert im Verhältnis zur beschriebenen Sättigungsmenge an. Da die absolute
Feuchtigkeit und der Sättigungsdruck jeweils in 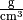 angegeben werden, ist die relative Luftfeuchtigkeit dimensionslos; sie wird
üblicherweise in Prozent angegeben. Mit speziellen Messgeräten (so genannten
„Hygrometern“) wird meist die relative Luftfeuchtigkeit gemessen.
angegeben werden, ist die relative Luftfeuchtigkeit dimensionslos; sie wird
üblicherweise in Prozent angegeben. Mit speziellen Messgeräten (so genannten
„Hygrometern“) wird meist die relative Luftfeuchtigkeit gemessen.
Beispiele:
In einem Volumen von
![V=\unit[1]{m^3}](../_images/math/4462803c72835a34fda258eec8867615b23c915a.png) ist bei einer Temperatur von
ist bei einer Temperatur von
![T=\unit[20]{\degree C}](../_images/math/ec9c56932f2049e6dba7387976aaa9cc41015933.png) eine Wassermenge von
eine Wassermenge von ![\unit[10]{g}](../_images/math/8ccff4cfbb2d8fa360abbd695222f3d0c5ab26ec.png) enthalten. Wie hoch ist die relative Luftfeuchtigkeit?
enthalten. Wie hoch ist die relative Luftfeuchtigkeit?Die Sättigungsmenge an Wasserdampf bei
![T=\unit[20]{\degree C}](../_images/math/ec9c56932f2049e6dba7387976aaa9cc41015933.png) beträgt
gemäß der obigen Tabelle beziehungsweise des obigen Diagramms ca.
beträgt
gemäß der obigen Tabelle beziehungsweise des obigen Diagramms ca.
![\unit[17]{\frac{g}{m^3}}](../_images/math/3c17d12aa44f84705ca5b8fc985d7eaffe93ae1e.png) . Teilt man die angegebene absolute
Luftfeuchtigkeit von
. Teilt man die angegebene absolute
Luftfeuchtigkeit von ![\unit[10]{\frac{g}{m^3}}](../_images/math/83128a854571f7358ed427f85a5ac799bbb57e8c.png) durch diesen
Sättigungswert, so erhält man eine relative Luftfeuchtigkeit von
durch diesen
Sättigungswert, so erhält man eine relative Luftfeuchtigkeit von
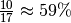 .
.Wie viel Gramm Wasser sind in einem Raum
![l=\unit[5]{m}](../_images/math/fadd9ffd3b0b5e107d6788ac4164bcc759ec983d.png) langen,
langen,
![b=\unit[4]{m}](../_images/math/984dc25a949bccca5e7a2cd92936349fb72da113.png) breiten und
breiten und ![h=\unit[2,5]{m}](../_images/math/1177234f065b6c6c861fd45317c7e240719497ee.png) hohen Raum
bei einer Temperatur von
hohen Raum
bei einer Temperatur von ![T_1=\unit[25]{\degree C}](../_images/math/a6d401065328eb59b58303841d923fcffbea1f94.png) und einer relativen
Luftfeuchtigkeit von
und einer relativen
Luftfeuchtigkeit von 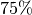 enthalten? Was passiert, wenn sich die
Temperatur auf
enthalten? Was passiert, wenn sich die
Temperatur auf ![T_2=\unit[15]{\degree C}](../_images/math/c8e025d9bab3f1403aa3baed041f3cc99a385975.png) abkühlt?
abkühlt?Das Volumen des Raums beträgt
![V=\unit[(5 \cdot 4 \cdot 2,5)]{m^3} =
\unit[50]{m^3}](../_images/math/9a90e9a9f87d905ab34eb7d73186fa82edf7913e.png) ; die Sättigungsmenge von Wasserdampf in Luft liegt bei einer
Temperatur von
; die Sättigungsmenge von Wasserdampf in Luft liegt bei einer
Temperatur von ![\unit[25]{\degree C}](../_images/math/3f7b5d8e775af1ae4b487a6fd9d1cf6ee8100555.png) bei rund
bei rund
![\unit[23]{\frac{g}{m^3}}](../_images/math/9ea019ca0ae89404b5902c317e58e3d12c5425fc.png) . Je Kubikmeter ist somit bei einer relativen
Luftfeuchtigkeit von
. Je Kubikmeter ist somit bei einer relativen
Luftfeuchtigkeit von 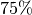 eine Menge von
eine Menge von ![0,75 \cdot
\unit[23]{g} = \unit[17,25]{g}](../_images/math/2d91d5e59b641f5673fd5d30018e5362ab99d2e5.png) an Wasserdampf enthalten. Insgesamt enthält
die Luft in dem Raum damit
an Wasserdampf enthalten. Insgesamt enthält
die Luft in dem Raum damit ![\unit[50]{m^3} \cdot
\unit[17,25]{\frac{g}{m^3}} \approx \unit[862,5]{g}](../_images/math/b81434ca43d0c10004bf1d8ae60b4f7d91e9bcac.png) .
.Nimmt die Temperatur der Luft ab, so sinkt auch die darin maximal mögliche Menge an Wasserdampf: Bei
![\unit[15]{\degree C}](../_images/math/a09f8f8e3bf8bcb2258fe49792e817a0d0ed68d5.png) beträgt die
Sättigungsmenge nur noch rund
beträgt die
Sättigungsmenge nur noch rund ![\unit[13]{\frac{g}{m^3}}](../_images/math/1bf7e33c6896832705fffcd8973d58e6dd4b2103.png) . Da in der Luft
jedoch
. Da in der Luft
jedoch ![\unit[17,25]{\frac{g}{m^3}}](../_images/math/142a61ddbe4194ae679d8aa7d9587d94994f4985.png) enthalten sind, werden je
Kubikmeter
enthalten sind, werden je
Kubikmeter ![\unit[17,25-13]{g} = \unit[4,25]{g}](../_images/math/9aa55fa703d246a5108653382aa9c2af8ab7e4ba.png) an Wasserdampf in Form
von feinen Nebeltröpfchen kondensieren; insgesamt
an Wasserdampf in Form
von feinen Nebeltröpfchen kondensieren; insgesamt ![\unit[(50 \cdot
4,25)]{g} = \unit[212,5]{g}](../_images/math/19c5dce8288a471602a23bff3062ecd021788a00.png) . Es wird folglich neblig, und die neue relative
Luftfeuchtigkeit beträgt
. Es wird folglich neblig, und die neue relative
Luftfeuchtigkeit beträgt 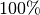 .
.Welche absolute Luftfeuchtigkeit hat Luft bei einer Temperatur von
![T_1=\unit[0]{\degree C}](../_images/math/2af97e4f113447da7e6c8756c62d4b8b009be6f9.png) und einer relativen Luftfeuchtigkeit von
und einer relativen Luftfeuchtigkeit von
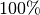 ? Welche relative Luftfeuchtigkeit stellt sich ein, wenn diese
Luft auf
? Welche relative Luftfeuchtigkeit stellt sich ein, wenn diese
Luft auf ![T_2=\unit[20]{\degree C}](../_images/math/a69a77e7df118cdf9f2f0f0cb00b8f4dbc209044.png) erwärmt wird?
erwärmt wird?Bei einer Temperatur von
![\unit[0]{\degree C}](../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) beträgt die
Sättigungsmenge an Wasserdampf knapp
beträgt die
Sättigungsmenge an Wasserdampf knapp ![\unit[5]{\frac{g}{m^3}}](../_images/math/a222e97ba0ef6fc10d2fa6f6505f1b7245a7e9ba.png) ; da die
Luft eine relative Luftfeuchtigkeit von
; da die
Luft eine relative Luftfeuchtigkeit von 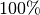 hat, enthält sie eben
diese Menge an Wasserdampf.
hat, enthält sie eben
diese Menge an Wasserdampf.Bei einer Temperatur von
![\unit[20]{\degree C}](../_images/math/5306d44af8f7df91464b32ed64cda4ded46190b0.png) beträgt die
Sättigungsmenge hingegen rund
beträgt die
Sättigungsmenge hingegen rund ![\unit[17]{g}](../_images/math/74ef6e19fa497b73f9271123215cc4396b48210c.png) . Die relative
Luftfeuchtigkeit der Luft beträgt nach dem Erwärmen somit etwa
. Die relative
Luftfeuchtigkeit der Luft beträgt nach dem Erwärmen somit etwa
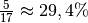 .
.
Wie das letzte Beispiel zeigt, kann auch bei kalter und nebliger Außenluft ein
kurzzeitiges Lüften ratsam, um die relative Luftfeuchtigkeit in einem Raum zu
senken. In Wohnräumen sind Luftfeuchtigkeiten zwischen 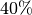 und
und
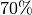 üblich. Luftfeuchtigkeiten von unter
üblich. Luftfeuchtigkeiten von unter 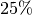 und über
und über
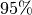 werden generell als unangenehm empfunden; in Gebäuden muss bei
einer konstanten Luftfeuchtigkeit von über
werden generell als unangenehm empfunden; in Gebäuden muss bei
einer konstanten Luftfeuchtigkeit von über 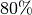 mit Schimmelbildung
gerechnet werden. In gefährdeten Räumen kann diesem durch häufiges, kurzzeitiges
Lüften und/oder durch kontinuierliches Lüften mit Wärmerückgewinnung
(„Wärmetauscher“) vorgebeugt werden.
mit Schimmelbildung
gerechnet werden. In gefährdeten Räumen kann diesem durch häufiges, kurzzeitiges
Lüften und/oder durch kontinuierliches Lüften mit Wärmerückgewinnung
(„Wärmetauscher“) vorgebeugt werden.
Phasendiagramme¶
Phasendiagramme werden üblicherweise in so genannten Phasendiagrammen
dargestellt. In einem derartigen Diagramm werden die Existenzbereiche der
einzelnen Phasen einer chemischen Substanz in Abhängigkeit von der (absoluten)
Temperatur 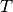 und dem vorherrschenden Druck
und dem vorherrschenden Druck  für jeweils
dargestellt.
für jeweils
dargestellt.
In einem Phasendiagramm sind die verschiedenen Bereiche, in denen jeweils nur ein Aggregatzustand existieren kann, durch Linien voneinander getrennt. Entlang der Linien kommt es zur so genannten Phasen-Koexistenz, in der jeweils zwei Phasen gleichberechtigt nebeneinander existieren. In jedem Phasendiagramm sind zudem zwei Punkte von besonderer Bedeutung:
- Der so genannte „Tripelpunkt“ gibt ein Temperatur-Druck-Wertepaar an, bei dem
alle drei Aggregatzustände (fest, flüssig und gasförmig) gleichzeitig
nebeneinander existieren. Bei Wasser beispielsweise liegt der Tripelpunkt bei einer
Temperatur von
![T=\unit[0,01]{\degree C}](../_images/math/73215491e331ac0760ea5c625b80e21bab9e82f9.png) und einem Druck von
und einem Druck von
![p=\unit[0,06]{bar}](../_images/math/00bf3ab6ec64b10486540d8ba876454551532fb3.png) .
. - Der so genannte „Kritische Punkt“ beschreibt das Ende der Siedepunktkurve,
also der Linie zwischen dem flüssigen und gasförmigen Aggregatzustand.
Oberhalb von diesem Punkt kann nicht mehr zwischen dem flüssigen und
gasförmigen Aggregatzustand unterschieden werden; man bezeichnet diesen
Zustand auch als „überkritisch“. Bei Wasser beispielsweise liegt der kritische
Punkt bei einer Temperatur von
![T=\unit[374]{\degree C}](../_images/math/b1454392ef473961eaa9de9e674ebf9ef4494580.png) und einem
Druck von
und einem
Druck von ![p=\unit[221]{bar}](../_images/math/b819441b324a3fd43550e3ed66b7586680fea0bf.png) .
.
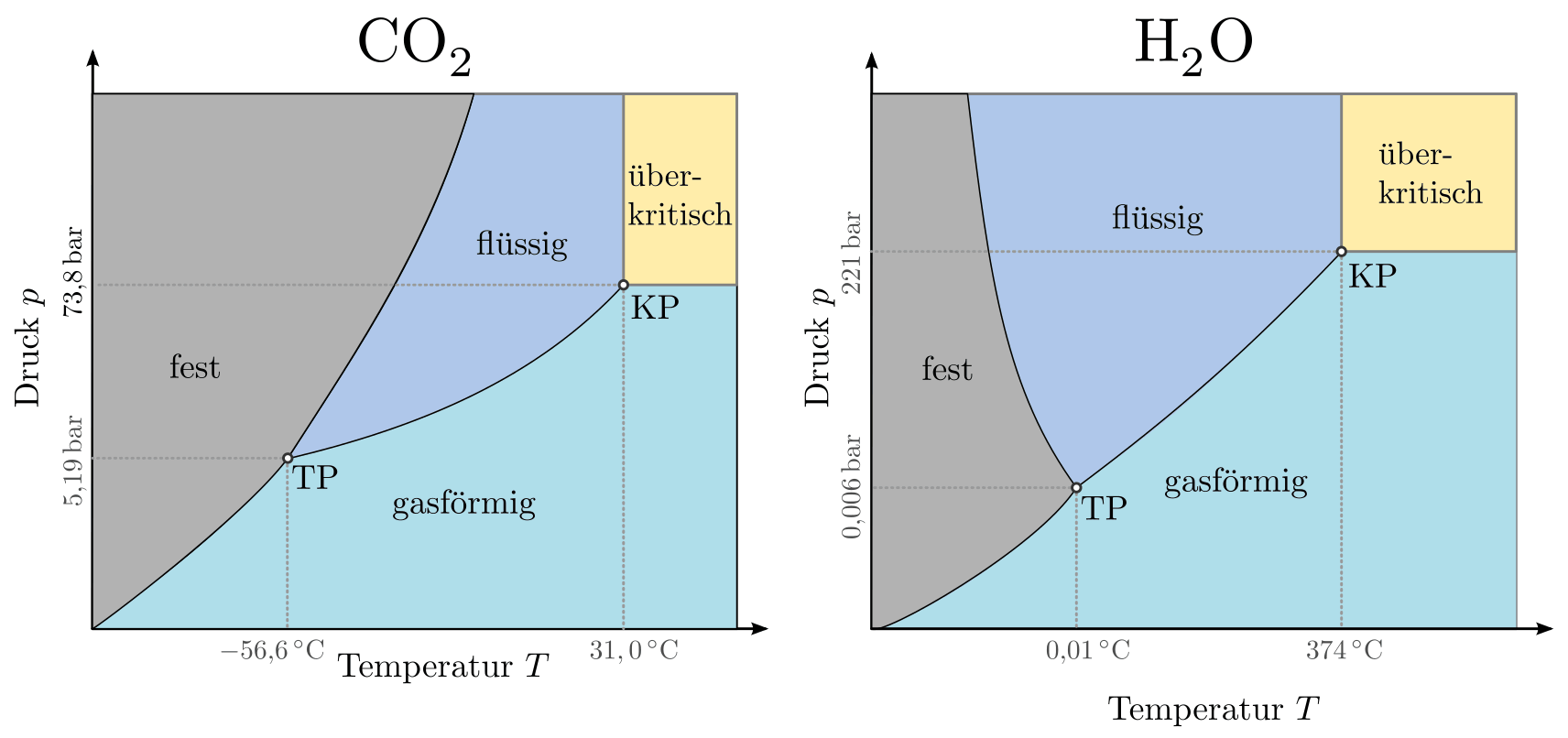
In der folgenden Abbildung ist links ein „typisches“ Phasendiagramm für eine gewöhnliche Substanz (als Beispiel Kohlenstoffdioxid), rechts ist ein Phasendiagramm für Wasser dargestellt. Die Besonderheit an dem Phasendiagramm von Wasser liegt darin, dass die Schmelzkurve (die Linie zwischen festem und flüssigen Aggregatzustand) eine negative Steigung aufweist. Daran kann man die Anomalie des Wassers erkennen: Es dehnt sich, anders als alle anderen bekannten Substanzen, beim Gefrieren aus.
Erhöht man vom Tripelpunkt ausgehend bei konstanter Temperatur den Druck beziehungsweise geht man im Diagramm vom Trippelpunkt aus senkrecht nach oben, so gelangt man gewöhnlich in die flüssige Phase; dies liegt daran, dass jedes physikalische System gern äußeren Zwängen ausweicht. Einem zunehmendem äußeren Druck weicht ein Stoff allgemein aus, indem er eine Phase annimmt, in der er weniger Volumen benötigt. Bei allen Substanzen außer Wasser wird durch einen hohen Druck somit das Erstarren begünstigt, bei Wasser hingegen das das Schmelzen.
Anmerkungen:
| [1] | Gibt ein Objekt im umgekehrten Fall Wärme ab, so verringert sich unter den gleichen Bedingungen (konstantes Volumen, gleicher Aggregatszustand) seine Temperatur. |
| [2] | Alte Fenster werden beispielsweise im Laufe der Zeit oben um wenige Atomlagen etwas dünner, unten dafür um wenige Atomlagen dicker. Dass viele antike Fenster im unteren Teil deutlich dicker sind als im oberen, hängt hingegen mit dem damaligen Herstellungsprozess zusammen. |
| [3] | Eine ausführlichere Erklärung hierfür liefert die in einem späteren Abschnitt näher beschriebene kinetische Gastheorie. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

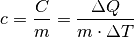
![\unit[(1013)]{hPa}](../_images/math/0821f2765ce9cce8f9ae023b358a4ea1525d01ad.png)
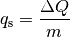
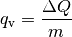
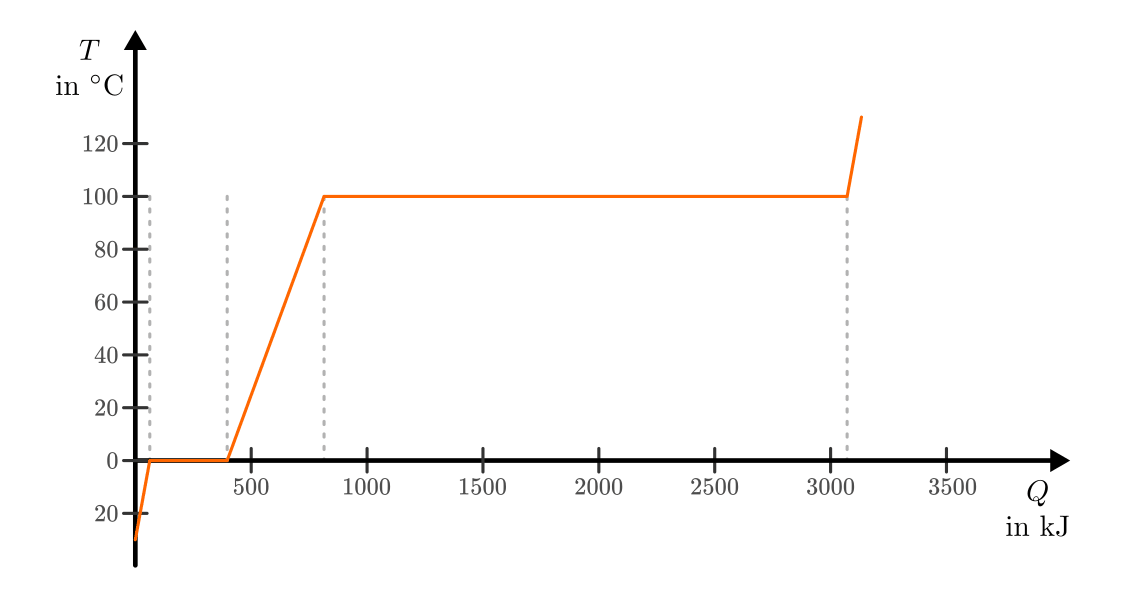
![\unit[-30]{\degree C}](../_images/math/272175655e42f6b2a476584dda980433a7f22b42.png) (Eis) bis
(Eis) bis ![\unit[+130]{\degree C}](../_images/math/f85e5565714a0e8912cd2c7bf9f9252ad34b5c76.png) (Dampf).
(Dampf).