Kraftwandler und Getriebe¶
Hebel¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Hebel.
Das Funktionsprinzip einer Balkenwaage beruht darauf, eine unbekannte Masse mit einer oder mehreren Massen bekannter Größe zu vergleichen. Da die Masse überall den gleichen Wert hat und die Gewichtskraft der unbekannten Masse in gleichem Maß vom Ort abhängt wie die der Vergleichs-Masse(n), funktioniert eine Balkenwaage an jeder beliebigen Stelle, also auch auf dem Mond.
Bei einer Federkraftwaage wird die Gewichtskraft einer unbekannten Masse mit der (bekannten) Spannkraft der Feder verglichen. Da auf dem Mond die Gewichtskraft der unbekannten Masse geringer ist, die Spannkraft der Feder jedoch gleich bleibt, zeigt eine Federkraftwaage auf dem Mond einen „falschen“ Wert an – die Skala müsste neu kalibriert werden.
Beim Öffnen einer Farbdose dient ein Schraubenzieher als Hebel. Die Länge des Kraftarms ist gleich der Strecke zwischen der Drehachse und dem Griff des Schraubenziehers. Die Länge des Lastarms ist gleich der Strecke zwischen der Drehachse und der Spitze des Schraubenziehers. Umso länger der Kraftarm im Vergleich zum Lastarm ist, desto weniger Kraft ist nötig, um den Deckel zu heben.
Beispiel:
Wenn der Abstand zwischen dem Dosenrand (der Drehachse) und Spitze des Schraubenziehers
![s_2 = \unit[0,01]{cm}](../../_images/math/a30e064389eb63e506c48e424655d26e014ac4b4.png) und der Abstand zum Griff
und der Abstand zum Griff
![s_1 = \unit[0,16]{m}](../../_images/math/c798b43036b25166c7425635ca1735d885bd8f73.png) beträgt, dann bewirkt eine Kraft
beträgt, dann bewirkt eine Kraft ![F_1 =
\unit[5]{N}](../../_images/math/82b81d7603af5736e7c8c4f84ade53d1e9f51305.png) am Griff eine Kraft von
am Griff eine Kraft von ![F_2 = \frac{s_1}{s_2} \cdot F_1 =
16 \cdot \unit[5]{N} = \unit[80]{N}](../../_images/math/0b93fdd736ff125c52e98c4ef35897d03cc5f6af.png) .
.
Damit die Balkenwaage als zweiseitiger Hebel im Gleichgewicht ist, müssen die auf der linken und auf der rechten Seite wirkenden Drehmomente
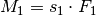 und
und 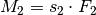 gleich groß sein:
gleich groß sein:![M_1 &= M_2 \\[4pt]
s_1 \cdot F_1 &= s_2 \cdot F_2](../../_images/math/febe16df52e817ead0460e520e72e44196e9a618.png)
Diese Gleichung kann nach der gesuchten Größe
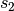 aufgelöst
werden:
aufgelöst
werden: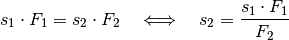
Die beiden wirkenden Kräfte
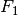 und
und 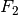 entsprechen jeweils
den Gewichtskräften
entsprechen jeweils
den Gewichtskräften 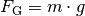 der beiden an der
Balkenwaage hängenden Lasten. Eingesetzt ergibt sich mit
der beiden an der
Balkenwaage hängenden Lasten. Eingesetzt ergibt sich mit ![m_1 =
\unit[2]{kg} ,\; m_2 = \unit[500]{g} = \unit[0,5]{kg}](../../_images/math/cd1c44fde6c6f86f3c353f855fa55a05ef7d50c7.png) und
und ![s_1 =
\unit[10]{cm} = \unit[0,1]{m}](../../_images/math/560d94b767898c9cf5700f75def4158a61566f9f.png) :
:![s_2 = \frac{s_1 \cdot F_1}{F_2} = \frac{ \unit[0,1]{m} \cdot
\unit[2]{kg} \cdot \unit[9,81]{\frac{N}{kg}} \cdot }{\unit[0,5]{kg} \cdot
\unit[9,81]{\frac{N}{kg}} } = \unit[0,4]{m} = \unit[40]{cm}](../../_images/math/d840c2d873701140743466362f9721ac1b56b364.png)
Die zweite Last, deren Masse nur ein Viertel der ersten Last beträgt, muss somit vier mal so weit entfernt von der Drehachse aufgehängt werden, damit die Balkenwaage im Gleichgewicht ist.
Beim Unterarm handelt es sich um einen einseitigen Hebel. Das in der Hand im Abstand
![s_2 = \unit[0,35]{m}](../../_images/math/bee8ef43d55aa3c93b309bbeca4ae1f9cf424c66.png) vom Ellenbogen gehaltene Gewicht hat eine
Gewichtskraft von
vom Ellenbogen gehaltene Gewicht hat eine
Gewichtskraft von ![F_2 = m \cdot g = \unit[2,00]{kg} \cdot
\unit[9,81]{\frac{N}{kg}} = \unit[19,62]{N}](../../_images/math/4e4142a9af4ca80599abf2c74bd04f398a8ced0c.png) .
.Das vom Gewicht bewirkte Drehmoment
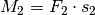 muss durch die
im Abstand
muss durch die
im Abstand ![s_1 = \unit[0,05]{m}](../../_images/math/58714798562dcf9ebe798718006e782961df1ae5.png) wirkende Kraft
wirkende Kraft 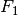 des
Muskels ausgeglichen werden. Da alle Kräfte senkrecht auf den Unterarm
einwirken, muss gelten:
des
Muskels ausgeglichen werden. Da alle Kräfte senkrecht auf den Unterarm
einwirken, muss gelten:![M_1 = M_2 \quad \Leftrightarrow \quad F_1 \cdot s_1 &= F_2 \cdot s_2
\\[6pt]
\Rightarrow F_1 = \frac{F_2 \cdot s_2}{s_1} = \unit[19,6]{N} \cdot
\frac{\unit[0,35]{m}}{\unit[0,05]{m}} \approx \unit[137]{N}](../../_images/math/d6da7c596a05c6d475c1473c69c9feef2762dd9f.png)
Der Muskel muss mit
![F_1 \approx \unit[137]{N}](../../_images/math/835c4c19d899686864e83e77fd3d5bb5659fdfa9.png) somit eine sieben mal
grössere Kraft aufbringen, als wenn das gleiche Gewicht bei vertikal
gehaltenem Unterarm getragen würde.
somit eine sieben mal
grössere Kraft aufbringen, als wenn das gleiche Gewicht bei vertikal
gehaltenem Unterarm getragen würde.
Damit sich der Hebel im Gleichgewicht befindet, muss die Summe der Drehmomente auf der linken Seite gleich der Summe der Drehmomente auf der rechten Seite des Hebels sein. Dies kann überprüft werden, indem man die jeweiligen Werte in die Drehmoment-Gleichung einsetzt und die erhaltenen Werte der Drehmomente miteinander vergleicht:
![M_{\mathrm{links}} = F_1 \cdot s_1 + F_2 \cdot s_2 = \unit[3,5]{N} \cdot
\unit[0,2]{m} + \unit[5]{N} \cdot \unit[0,1]{m} = \unit[1,2]{N \cdot m}
\\[4pt]
M_{\mathrm{rechts}} = F_3 \cdot s_3 + F_4 \cdot s_4 = \unit[1,5]{N} \cdot
\unit[0,6]{m} + \unit[4]{N} \cdot \unit[0,075]{m} = \unit[1,2]{N \cdot m}](../../_images/math/70ea4174550958414939b3d7a43a25477644c1d7.png)
Die Drehmomente auf der linken und auf der rechten Seite sind gleich groß, der Hebel befindet sich somit im Gleichgewicht.
Schiefe Ebene¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Schiefe Ebene.
Entlang einer schiefen Ebene gilt als Kraftverhältnis:
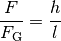
Die Höhe
![h=\unit[0,4]{m}](../../_images/math/e02c83289b1026900e3746377587cbfdaf5bd9ae.png) der schiefen Ebene sowie ihre Länge
der schiefen Ebene sowie ihre Länge
![l= \unit[2,4]{m}](../../_images/math/b3a1c8f8df6e5cbb02cb13048f90a2d60afd12ff.png) sind gegeben, auch die Gewichtskraft
sind gegeben, auch die Gewichtskraft ![F
_{\mathrm{G}}=\unit[600]{N}](../../_images/math/734fbf1b8427324a39d1495885c815e4f1e287ca.png) der Schubkarre ist bekannt. Löst man die obige
Gleichung nach der Kraft
der Schubkarre ist bekannt. Löst man die obige
Gleichung nach der Kraft  auf, so erhält man nach Einsetzen der
gegeben Werte die gesuchte Kraft.
auf, so erhält man nach Einsetzen der
gegeben Werte die gesuchte Kraft.![F = \frac{F_{\mathrm{G}} \cdot h}{l} = \frac{\unit[600]{N} \cdot
\unit[0,6]{m}}{\unit[2,4]{m}} = \unit[150]{N}](../../_images/math/20ab1707b10e1eff68a6ef79de1578c4918a4a7b.png)
Die zum Schieben der Schubkarre nötige Kraft beträgt somit
![\unit[150]{N}](../../_images/math/f19d573cc1f000d0c04153a904f01f6a23e76970.png) .
.
Flaschenzüge und Rollen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Flaschenzüge und Rollen.
Bei einem Flaschenzug mit
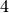 losen Rollen wird die Last gleichmäßig auf
losen Rollen wird die Last gleichmäßig auf
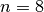 Seilstücke verteilt. Die nötige Zugkraft
Seilstücke verteilt. Die nötige Zugkraft 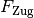 am losen Seilende beträgt, von Reibungskräften abgesehen, folglich auch nur
am losen Seilende beträgt, von Reibungskräften abgesehen, folglich auch nur
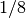 der Gewichtskraft
der Gewichtskraft 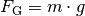 der Last. Zur
Masse
der Last. Zur
Masse ![m = \unit[200]{kg}](../../_images/math/72d5c638e8757e333ccde6db3b4c098e8112fbe7.png) der Last muss allerdings die Masse
der Last muss allerdings die Masse ![m =
\unit[4 \cdot 5]{kg}](../../_images/math/98b3db25fb556acbdf173776e000c97fa6db593f.png) der losen Rollen hinzu addiert werden, da diese
ebenfalls mit angehoben werden.
der losen Rollen hinzu addiert werden, da diese
ebenfalls mit angehoben werden.![F_{\mathrm{Zug}} = \frac{F_{\mathrm{G}}}{n} = \frac{m \cdot g}{n} =
\frac{\unit[220]{kg} \cdot \unit[9,81]{\frac{N}{kg} }}{8} =
\unit[269,8]{N}](../../_images/math/94c839e04dfaa1c937b00ff76332e340d1fd7408.png)
Anstelle
![F_{\mathrm{G}} = \unit[200]{kg} \cdot \unit[9,81]{N/kg } =
\unit[1962]{N}](../../_images/math/07c93f0d7e24de06e1d0f5f2460a31e4753de0df.png) muss somit nur etwas mehr als ein Achtel des Kraftwertes, also
muss somit nur etwas mehr als ein Achtel des Kraftwertes, also
![\unit[269,8]{N}](../../_images/math/5dd51e5f739747bea325aadfb450b67334155fd5.png) , aufgewendet werden. Gleichzeitig muss das Seil um die
, aufgewendet werden. Gleichzeitig muss das Seil um die
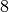 -fache Weglänge, also um
-fache Weglänge, also um ![8 \cdot \unit[3]{m} = \unit[24]{m}](../../_images/math/299ce546c56558681058e135bd9031abf764d447.png) ,
angehoben werden.
,
angehoben werden.
Bei einem Flaschenzug mit
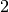 losen Rollen wird die Last gleichmäßig
auf
losen Rollen wird die Last gleichmäßig
auf 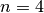 tragende Seilstücke verteilt. Die Zugkraft
tragende Seilstücke verteilt. Die Zugkraft 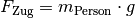 am losen Seilende kann entsprechend,
wenn keine Reibungskräfte auftreten und das Gewicht des Flaschenzugs
vernachlässigbar ist, auch eine
am losen Seilende kann entsprechend,
wenn keine Reibungskräfte auftreten und das Gewicht des Flaschenzugs
vernachlässigbar ist, auch eine 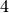 -fach höhere Last
-fach höhere Last 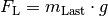 anheben.
anheben.![F_{\mathrm{Zug}} = \frac{F_{\mathrm{Last}}}{n} \quad &\Longleftrightarrow
\quad F_{\mathrm{Last}} = n \cdot F_{\mathrm{Zug}} \\[8pt]
m_{\mathrm{Last}} \cdot g &= n \cdot m_{\mathrm{Person}} \cdot g \\[6pt]
m_{\mathrm{Last}} = n \cdot m_{\mathrm{Person}} &= 4 \cdot \unit[50]{kg}
= \unit[200]{kg}](../../_images/math/47d54ad8f4897afaa554830c99eeaaf9e0eb09d7.png)
Eine
![\unit[50]{kg}](../../_images/math/ace271226a971d2a199f66cd92cc0e82f4d9675c.png) schwere Person kann somit mit Hilfe des
Flaschenzugs eine Last mit einer Masse von maximal
schwere Person kann somit mit Hilfe des
Flaschenzugs eine Last mit einer Masse von maximal ![\unit[200]{kg}](../../_images/math/3f5499e35faad33a8f52ae9756efd7338ebd875b.png) anheben.
anheben.
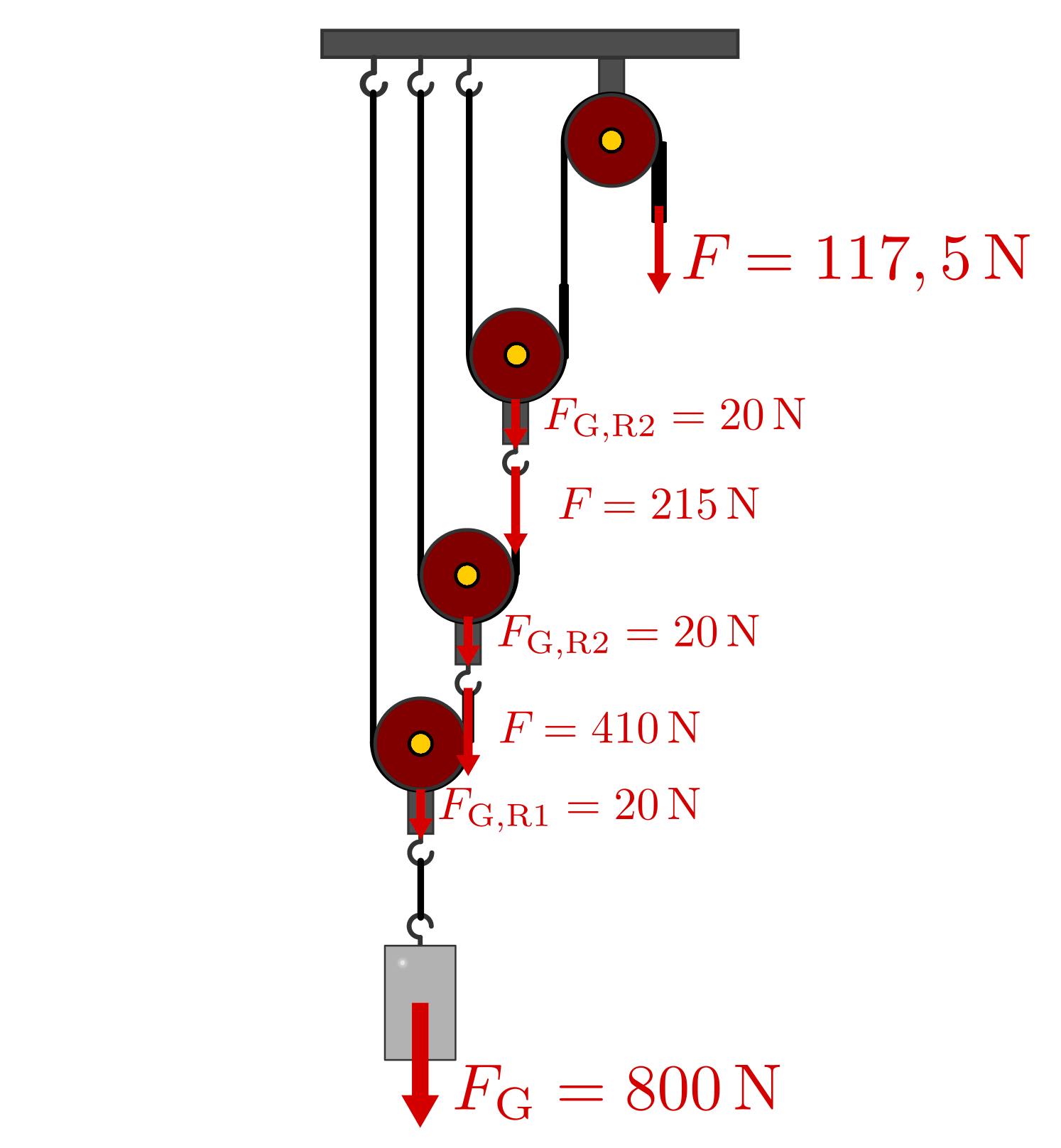
Bei einem Potenzflaschenzug wird die zum Anheben der Last nötige Kraft an jeder losen Rolle halbiert. Bei
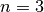 Rollen ist – sofern man ihr
Eigengewicht und die Reibung vernachlässigen kann – zum Anheben einer Last
mit einem Gewicht von
Rollen ist – sofern man ihr
Eigengewicht und die Reibung vernachlässigen kann – zum Anheben einer Last
mit einem Gewicht von ![F_{\mathrm{G}} = \unit[800]{kg}](../../_images/math/0cbeea856d5ee91879545deb9d3f26a136988a7d.png) somit nur folgende
Kraft
somit nur folgende
Kraft  nötig:
nötig:![F = \frac{1}{2^n} \cdot F_{\mathrm{G}} = \frac{1}{2^3} \cdot \unit[800]{N} =
\frac{1}{8} \cdot \unit[800]{N} = \unit[100]{N}](../../_images/math/3e21a0cafb1110b3723450d9b597d6c34d1080e0.png)
Die zum Anheben nötige Kraft beträgt also mindestens
![F=\unit[100]{N}](../../_images/math/f77349e25c1fc97050775092539d62f938711542.png) .
Berücksichtigt man das Eigengewicht
.
Berücksichtigt man das Eigengewicht ![F_{\mathrm{G,R}} = \unit[20]{N}](../../_images/math/f708846d89ce86d8f64d1d93ecae4178de7f068d.png) der einzelnen Rollen, so muss dieser Betrag an jeder losen Rolle zur
jeweiligen Last hinzuaddiert werden.
der einzelnen Rollen, so muss dieser Betrag an jeder losen Rolle zur
jeweiligen Last hinzuaddiert werden.Zum Anheben der Last ist in diesem Fall, wie in der obigen Abbildung gezeigt, eine Kraft von
![F = \unit[117,5]{N}](../../_images/math/f930846ec21dbe2cfe354e0f860012de0a42095f.png) nötig.
nötig.
Zahnräder und Getriebe¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Zahnräder und Getriebe.
Die Kurbel und das vordere Zahnrad sind fest miteinander verbunden, ebenso das hintere Zahnrad und die Felge des Hinterrads. In diesen beiden Teile-Kombinationen sind die wirkende Drehmomente jeweils gleich. Somit kann als zunächst die Kraft
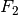 berechnet werden, die das vordere Zahnrad
auf die Kette ausübt. Für das Drehmoment, das der Fahrer auf die Kurbel
ausübt, gilt:
berechnet werden, die das vordere Zahnrad
auf die Kette ausübt. Für das Drehmoment, das der Fahrer auf die Kurbel
ausübt, gilt:![M_1 = F_1 \cdot r_1 = \unit[50]{N} \cdot \unit[0,2]{m} = \unit[10]{Nm}](../../_images/math/097046c28af01831c0aa6a5da41a912720d057da.png)
Das gleiche Drehmoment tritt auch im vorderen Zahnrad auf; da es jedoch einen kleineren Radius
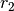 als die Kurbel hat, muss die auf die Kette
wirkende Kraft
als die Kurbel hat, muss die auf die Kette
wirkende Kraft 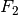 entsprechend größer sein:
entsprechend größer sein:![M_1 = M_2 \quad \Leftrightarrow \quad F_1 \cdot r_1 = F_2 \cdot r_2 \\[6pt]
\Rightarrow F_2 = \frac{r_1}{r_2} \cdot F_1 =
\frac{\unit[0,2]{m}}{\unit[0,1]{m}} \cdot \unit[50]{N} = \unit[100]{N}](../../_images/math/a307c53b7d9795a9b29cf46dfdcf6b85598a5397.png)
Auf die Kette wird somit eine Zugkraft von
![F_2 = \unit[100]{N}](../../_images/math/d039267f63f362e70d319945b5a848044eceba94.png) ausgeübt. Die Kette überträgt diese Kraft auf das hintere Zahnrad, so dass an
diesem eine gleich große Kraft
ausgeübt. Die Kette überträgt diese Kraft auf das hintere Zahnrad, so dass an
diesem eine gleich große Kraft 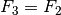 angreift. Für das Drehmoment
angreift. Für das Drehmoment
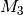 am hinteren Zahnrad gilt somit:
am hinteren Zahnrad gilt somit:![M_3 = F_3 \cdot r_3 = \unit[100]{N} \cdot \unit[0,05]{m} = \unit[5]{Nm}](../../_images/math/edaab31e481d406a0080e1fe5d5d2c12a13bb658.png)
Das gleiche Drehmoment wirkt wegen der starren Verbindung mit dem hinteren Zahnrad auch in der Felge; da diese jedoch einen größeren Radius
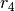 hat, ist die zugehörige Kraft
hat, ist die zugehörige Kraft 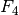 am Umfang entsprechend geringer:
am Umfang entsprechend geringer:![M_3 = M_4 \quad \Leftrightarrow \quad F_3 \cdot r_3 = F_4 \cdot r_4
\\[6pt] \Rightarrow F_4 = \frac{r_3}{r_4} \cdot F_3 =
\frac{\unit[0,05]{m}}{\unit[0,35]{m}} \cdot \unit[100]{N} \approx
\unit[14,3]{N}](../../_images/math/b87e78f3748d375e581f3e56ceab58ff29d13f1f.png)
Die auf die Pedale einwirkende Kraft von
![F_1 = \unit[50]{N}](../../_images/math/75ad86317c69d17efe00e86df6d643945dc9f54b.png) beschleunigt somit die Felge mit
beschleunigt somit die Felge mit ![F \approx \unit[14,3]{N}](../../_images/math/6239deaed290c5be6672c4b95b5c7ce4e799b9c2.png) beziehungsweise kann – beispielsweise mittels Bremsbacken – durch eine
solche an der Felge angreifende Kraft ausgeglichen werden.
beziehungsweise kann – beispielsweise mittels Bremsbacken – durch eine
solche an der Felge angreifende Kraft ausgeglichen werden.Schaltet man bei gleicher Tretkraft
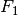 vorne auf ein kleines Zahnrad
vorne auf ein kleines Zahnrad
![(r_2 = \unit[5]{cm})](../../_images/math/587f95dd57c5280b9a89287b27e86eaa9f564bd8.png) herunter, so muss die dort wirkende Kraft
herunter, so muss die dort wirkende Kraft
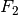 wegen des nur halb so großen Radius doppelt so groß sein, um ein
gleiches Drehmoment zu bewirken. Die Auf die Kette wirkende Kraft ist also mit
wegen des nur halb so großen Radius doppelt so groß sein, um ein
gleiches Drehmoment zu bewirken. Die Auf die Kette wirkende Kraft ist also mit
![F_2 = \unit[200]{N}](../../_images/math/0c2199909eb28604cbe29dd47a19127e089804b7.png) doppelt so groß. Am hinteren Rad bleibt alles
unverändert, so dass die Kette dort ein doppelt so großes Drehmoment bewirkt
und folglich auch die Kraft auf die Felge doppelt so groß wird, also
doppelt so groß. Am hinteren Rad bleibt alles
unverändert, so dass die Kette dort ein doppelt so großes Drehmoment bewirkt
und folglich auch die Kraft auf die Felge doppelt so groß wird, also
![F_4 \approx \unit[28,6]{N}](../../_images/math/f79d9d63a416aebf7eb92f0110e3d365fadfb740.png) gilt.
gilt.