Zahnräder und Getriebe¶
Zahnrad und Zahnstange¶
Ein Zahnrad ist ein Rad, entlang dessen Umfang Zahnungen eingearbeitet sind. Mittels dieser Zahnungen kann ein Zahnrad ein wirkendes Drehmoment beispielsweise auf eine Kette oder ein anderes Zahnrad übertragen.
Werden mehrere Zahnräder miteinander kombiniert, so bezeichnet man die
Konstruktion als Getriebe. Zwei Räder wirken dabei stets mit gleich großer Kraft
 aufeinander ein. Sind allerdings die Radien
aufeinander ein. Sind allerdings die Radien 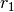 und
und
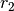 der Zahnräder unterschiedlich groß, so sind jeweils auch die
wirkenden Drehmomente
der Zahnräder unterschiedlich groß, so sind jeweils auch die
wirkenden Drehmomente 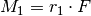 und
und 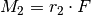 verschieden.
verschieden.
Übersetzungs- und Größenverhältnisse
Für das so genannte „Übersetzungsverhältnis“ eines Getriebes, d.h. das Verhältnis der wirkenden Drehmomente, gilt die folgende Formel:[1]
(1)¶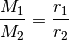
Die wirkenden Drehmomente stehen somit im gleichen Größenverhältnis zuinander wie die Radien der aufeinander einwirkenden Zahnräder.
Aufgrund der Zahnungen kann bei Zahnrädern kein Durchrutschen („Schlupf“) auftreten, die aufeinander einwirkenden Oberflächen legen also stets den gleichen Weg zurück. Dies hat zweierlei Konsequenzen:
Die Zahnungen von zueinander passenden Zahnrädern müssen stets gleich groß sein. Bei einem Zahnrad mit einem Vielfachen an Zahnungen muss somit auch der Radius um ein entsprechendes Vielfaches größer sein.[2] Sind
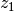 und
und 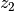 die Anzahl an Zahnungen zweier Zahnräder aufeinander folgender
Zahnräder und
die Anzahl an Zahnungen zweier Zahnräder aufeinander folgender
Zahnräder und 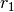 und
und 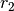 die zugehörigen Radien, so gilt:
die zugehörigen Radien, so gilt:(2)¶
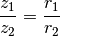
Die Anzahl der Zahnungen ist somit direkt proportional zum Radius der Zahnräder.
Kleine Zahnräder müssen sich in einem Getriebe entsprechend „schneller“, also mit einer höheren Winkelgeschwindigkeit
 drehen als große
Zahnräder. Sind
drehen als große
Zahnräder. Sind 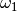 und
und 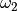 die
Winkelgeschwindigkeiten zweier aufeinander folgender Zahnräder und
die
Winkelgeschwindigkeiten zweier aufeinander folgender Zahnräder und 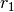 und
und 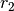 die zugehörigen Radien, so gilt:[3]
die zugehörigen Radien, so gilt:[3](3)¶
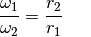
Die Winkelgeschwindigkeiten sind somit umgekehrt proportional zu den Radien der Zahnräder.
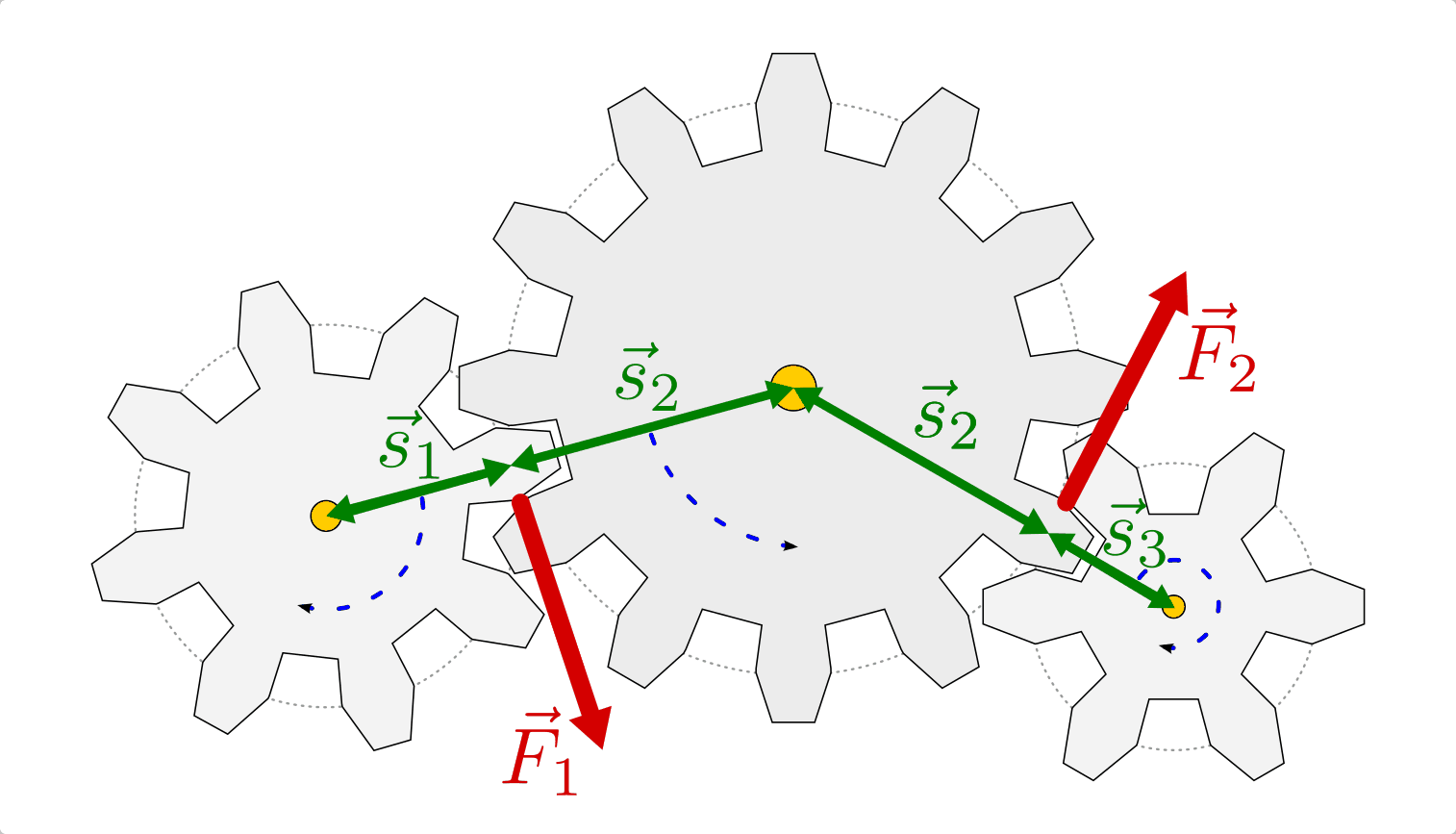
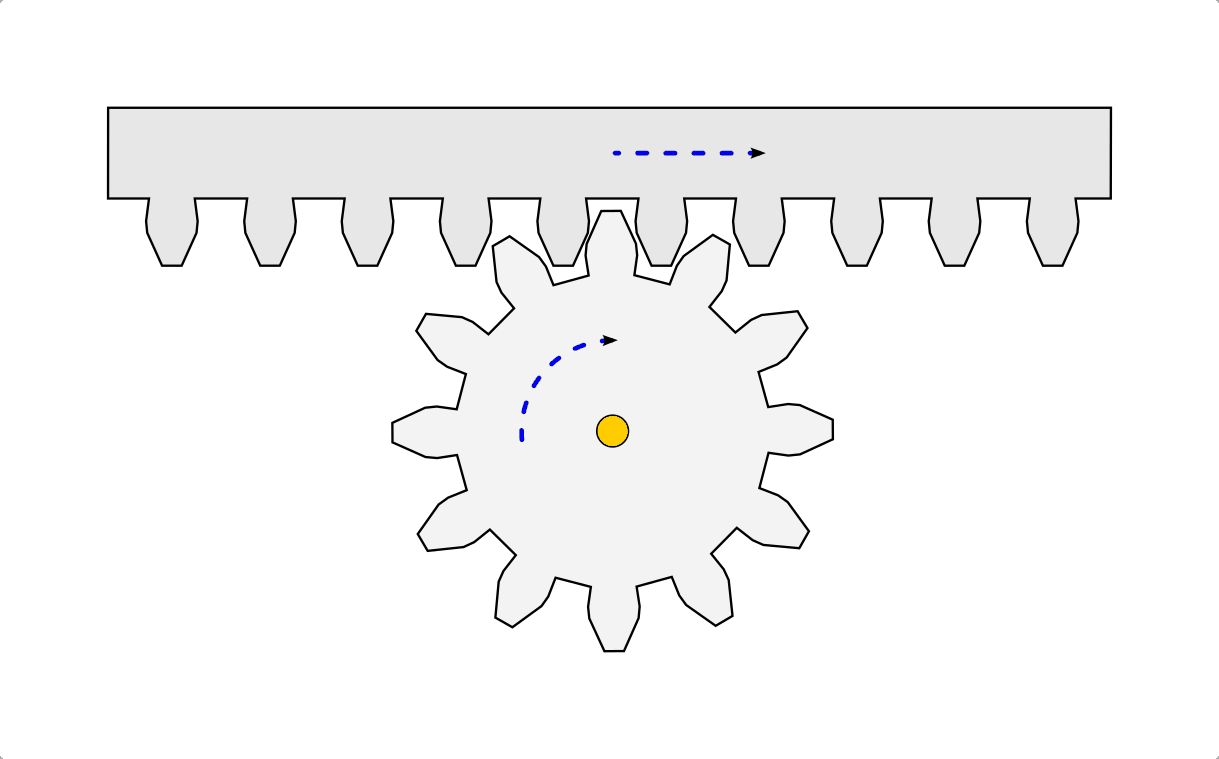
Wirken zwei Zahnräder direkt aufeinander ein, so kehrt sich die Drehrichtung um (in Abbildung Zahnrad-Getriebe ist dies anhand der gestrichelten blauen Pfeile zu erkennen). Ist eine Umkehrung der Drehrichtung nicht beabsichtigt, so kann ein drittes Zahnrad mit beliebiger Größe dazwischen angeordnet werden.
Zahnstangen
Zahnräder werden in Getrieben häufig auch in Kombination mit so genannten Zahnstangen eingesetzt. Hierdurch kann die rotierende Bewegung eines Zahnrads in eine geradlinige Bewegung der Zahnstange umgesetzt werden. Ist die Zahnstange fest und das Zahnrad beweglich, wie es beispielsweise bei einer Zahnradbahn der Fall ist, so ist auch ein schlupffreier Antrieb des Zahnrads gegenüber der Zahnstange möglich.
Riemen- und Kettengetriebe¶
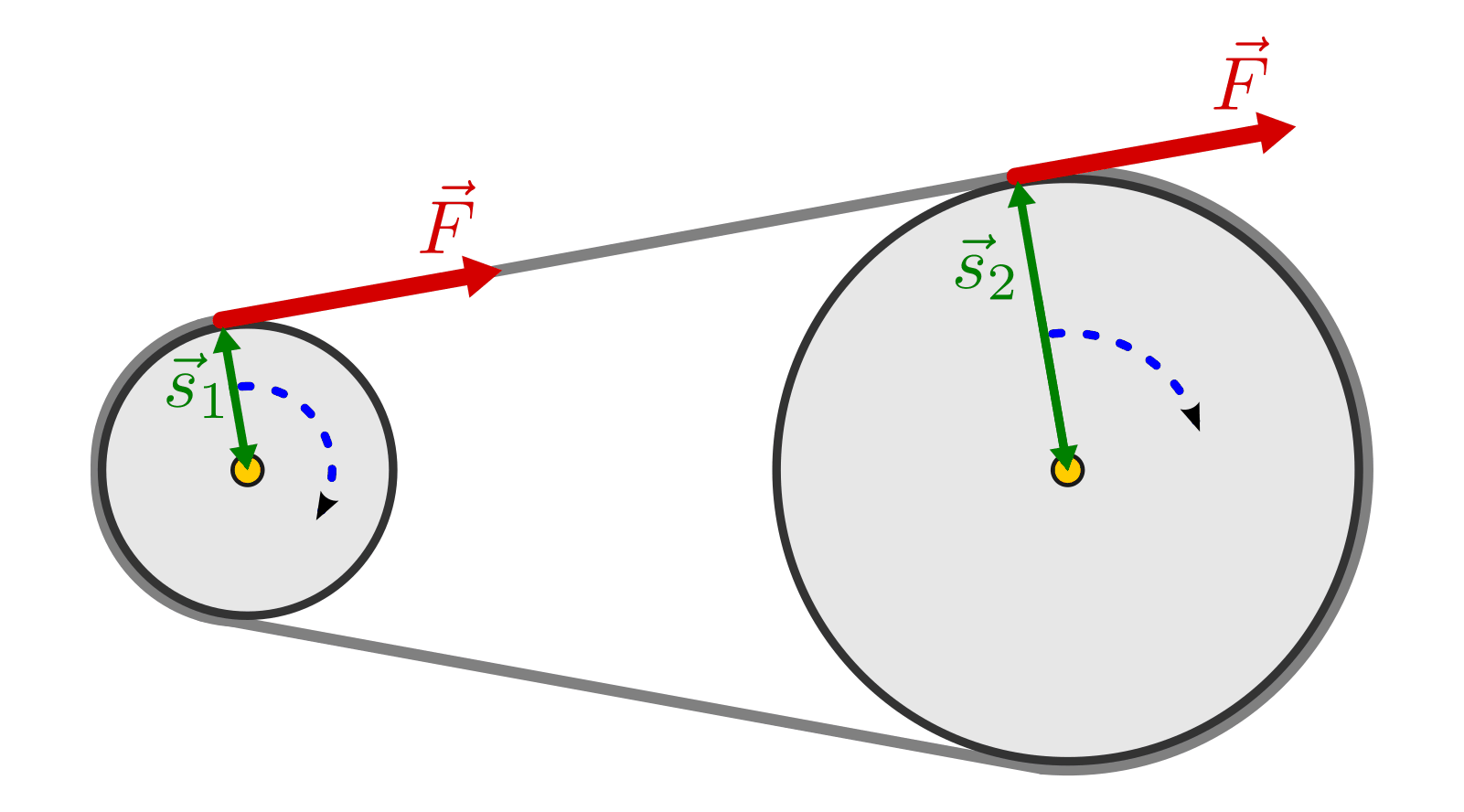
Mittels eines Riemens kann der Angriffspunkt einer (Zug-)Kraft in Richtung des Riemens verschoben werden. Wird ein Riemen über zwei Riemenscheiben mit unterschiedlichem Durchmesser geführt, so lässt sich bei ausreichender Spannung des Riemens eine Kraft von der einen Riemenscheibe auf die andere übertragen.
Die übertragene Kraft  ist an allen Stellen des Riemens und auch an den
Angriffspunkten der Riemenscheiben gleich groß; bei unterschiedlichen Radien
ist an allen Stellen des Riemens und auch an den
Angriffspunkten der Riemenscheiben gleich groß; bei unterschiedlichen Radien
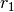 und
und 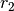 der Scheiben sind jedoch die wirkenden Drehmomente
der Scheiben sind jedoch die wirkenden Drehmomente
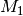 und
und 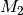 verschieden groß.
verschieden groß.
Erfolgt die Kraftübertragung von der kleineren Riemenscheibe auf die größere, so erfährt diese aufgrund ihres größeren Durchmessers auch ein entsprechend größeres Drehmoment. Im gleichen „Übersetzungsverhältnis“ nimmt die Rotationsfrequenz bei der größeren Riemenscheibe ab.
Wird in einem Riemengetriebe die Spannung des Riemens gelockert, üblicherweise durch ein leichtes Verschieben der angetriebenen Riemenscheibe, so dreht die antreibende Riemenscheibe „leer“ durch, und es kann keine Kraftübertragung erfolgen. Dieser Effekt wird beispielsweise in Rasenmähern in Form einer Kupplung genutzt, die bei Bedarf auf Leerlauf geschaltet werden kann. Gleichermaßen kann die antreibende Riemenscheibe allerdings auch durchdrehen, wenn die anzutreibende Riemenscheibe einen zu großen Drehwiderstand entgegensetzt, der Riemen sich also nicht bewegen lässt. Eine derartig starke (unbeabsichtigte) Reibung hat in der Regel auch einen starken Verschleiß des Riemens zur Folge.
Sind (zu) hohe Belastungen im normalen Betrieb nicht auszuschließen, können anstelle von Riemen auch Riemen mit Zahnungen („Zahnriemen“) oder, als stabilste Variante, Ketten mit passenden Zahnrädern zur Kraftübertragung verwendet werden. Durch die so genannte „Formschlüssigkeit“ können höhere Kräfte übertragen werden, ohne dass ein Schlupf der Kette auftreten kann.
Anmerkungen:
| [1] | Die Formel für das Übersetzungsverhältnis zweier Zahnräder kann
anhand der Formeln für die wirkenden Drehmomente
Da an zwei Zahnrädern paarweise stets die gleiche Kraft wirkt, können die
beiden obigen Gleichungen jeweils nach
Stellt man diese Gleichung mittels Multiplikation mit |
| [2] | Allgemein muss der Umfang eines Zahnrads stets einem Vielfachen der
Länge
Hierbei ist |
| [3] | Die aufeinander einwirkenden Zahnungen haben zwar eine gleiche
Bahngeschwindigkeit
Stellt man diese Gleichung mittels Division durch |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

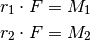
![\left.\begin{aligned}
F = \frac{M_1}{r_1} \\[4pt]
F = \frac{M_2}{r_2}
\end{aligned} \; \right\}
\quad \Rightarrow \quad \frac{M_1}{r_1} = \frac{M
_2}{r_2}{\color{white}.}](../../_images/math/d7ba0be129eae52348628bc8e308b552eed56be0.png)
 einer einzelnen Zahnung entsprechen. Es gilt also:
einer einzelnen Zahnung entsprechen. Es gilt also: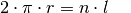
 die Anzahl der Zahnungen eines Zahnrads.
die Anzahl der Zahnungen eines Zahnrads. . Bei unterschiedlichen Radien
. Bei unterschiedlichen Radien ![{\color{white}\ldots}\left.\begin{aligned}
v = \omega_1 \cdot r_1 \\[4pt]
v = \omega_2 \cdot r_2
\end{aligned} \; \right\}
\quad \Rightarrow \quad \omega_1 \cdot r_1 = \omega_2 \cdot r_2](../../_images/math/0fca6483e6bda8f172158677349a9fdd8c8d36e0.png)