Schiefe Ebenen¶
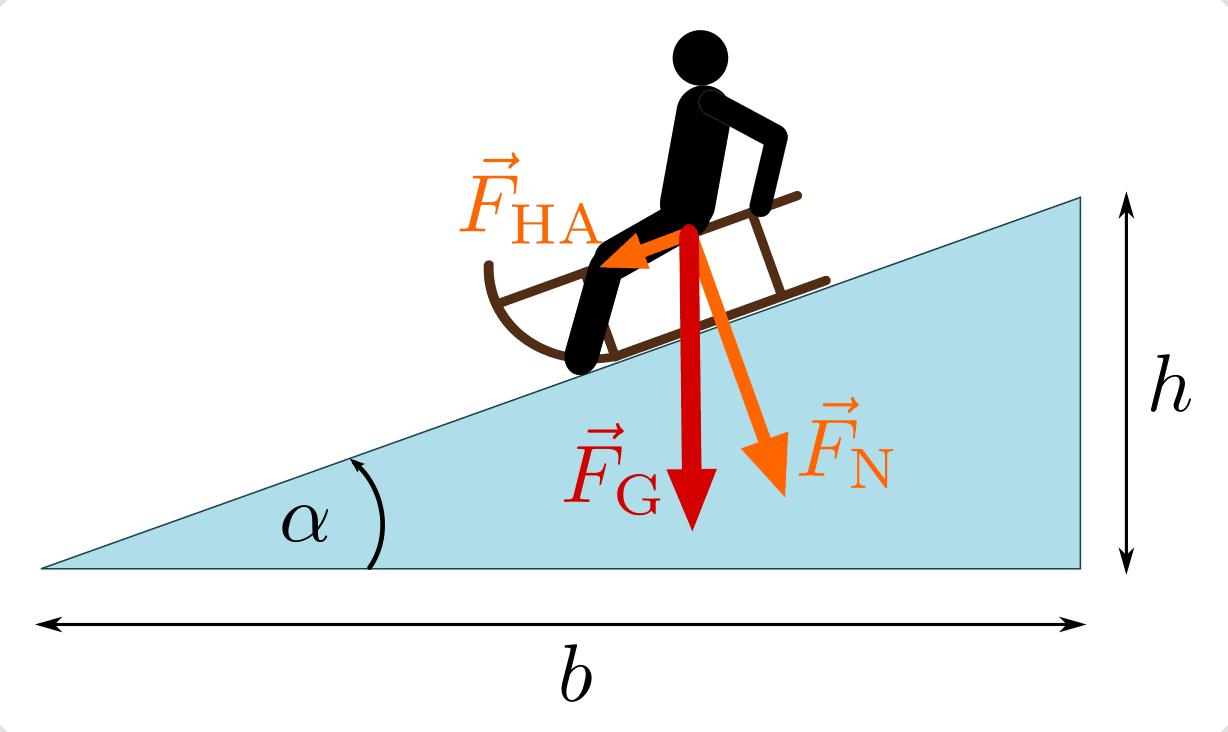
Wird ein Körper auf eine schiefe Ebene gestellt, so wird er aufgrund seiner
Gewichtskraft 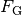 entlang der schiefen Ebene hangabwärts
beschleunigt. Dies lässt sich erklären, wenn man die Gewichtskraft in zwei
Teilkräfte (entlang der schiefen Ebene und senkrecht zu ihr) zerlegt denkt:
entlang der schiefen Ebene hangabwärts
beschleunigt. Dies lässt sich erklären, wenn man die Gewichtskraft in zwei
Teilkräfte (entlang der schiefen Ebene und senkrecht zu ihr) zerlegt denkt:
- Die Kraft senkrecht zur schiefen Ebene wird Normalkraft
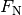 genannt. Dieser Kraftanteil würde ein Einsinken des Körpers in die schiefe
Ebene bewirken, jedoch wirkt bei einem festen Untergrund der Boden aufgrund
seiner Starrheit dagegen.
genannt. Dieser Kraftanteil würde ein Einsinken des Körpers in die schiefe
Ebene bewirken, jedoch wirkt bei einem festen Untergrund der Boden aufgrund
seiner Starrheit dagegen. - Die Kraft parallel zur schiefen Ebene wird Hangabtriebskraft
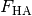 genannt. Dieser Kraftanteil bewirkt eine Beschleunigung des
Körpers entlang der schiefen Ebene.
genannt. Dieser Kraftanteil bewirkt eine Beschleunigung des
Körpers entlang der schiefen Ebene.
Ist die Hangabtriebskraft groß genug, um die zwischen Körper und schiefer Ebene wirkende Reibungskraft zu überwinden, so beginnt der Körper zu gleiten.
Auf einer waagrechten Ebene ist die Gewichtskraft 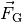 gleich der Normalkraft
gleich der Normalkraft 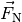 , der Betrag der
Hangabtriebskraft ist gleich Null. Umgekehrt ist entlang einer vertikalen Wand
die Hangabtriebskraft gleich der Gewichtskraft, und die (anpressende)
Normalkraft ist gleich Null. Bei einem beliebigen Winkel
, der Betrag der
Hangabtriebskraft ist gleich Null. Umgekehrt ist entlang einer vertikalen Wand
die Hangabtriebskraft gleich der Gewichtskraft, und die (anpressende)
Normalkraft ist gleich Null. Bei einem beliebigen Winkel  der
schiefen Ebene gelten für die Beträge der Normal- und Hangabtriebskraft folgende
Zusammenhänge:
der
schiefen Ebene gelten für die Beträge der Normal- und Hangabtriebskraft folgende
Zusammenhänge:
(1)¶![F_{\mathrm{HA}} &= F_{\mathrm{G}} \cdot \sin{\alpha }\\[6pt]
F_{\mathrm{N\phantom{A}}} &= F_{\mathrm{G}} \cdot \cos{\alpha }](../../_images/math/fe22bfaa079d25048473700a4c6e9f10b4a05a79.png)
Hierbei wurde die genutzt, dass der Winkel zwischen der Gewichtskraft 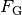 und Normalkraft
und Normalkraft 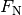 gleich dem Winkel
gleich dem Winkel  der schiefen Ebene ist, da es sich um zwei senkrecht zueinander stehende
Winkel handelt. Bezeichnet man zusätzlich
mit
der schiefen Ebene ist, da es sich um zwei senkrecht zueinander stehende
Winkel handelt. Bezeichnet man zusätzlich
mit  die Länge der schiefen Ebene, so ergibt sich aufgrund der
Ähnlichkeit der beiden Kraftdreiecke und des Dreiecks der Schiefen Ebene
folgender Zusammenhang zwischen der Hangabtriebskraft und der Gewichtskraft des
Schlittens:
die Länge der schiefen Ebene, so ergibt sich aufgrund der
Ähnlichkeit der beiden Kraftdreiecke und des Dreiecks der Schiefen Ebene
folgender Zusammenhang zwischen der Hangabtriebskraft und der Gewichtskraft des
Schlittens:
(2)¶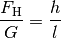
Je länger also die schiefe Ebene ist, desto kleiner ist die entlang der Ebene wirkende Hangabtriebskraft. Aus diesem Grund werden in Gebirgen Straßen und Wege in Serpentinen angelegt.
Die Größe des Winkels  lässt sich anhand des Verhältnis der Höhe
lässt sich anhand des Verhältnis der Höhe
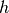 zur (horizontalen) Breite
zur (horizontalen) Breite 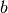 der schiefen Ebene berechnen.
Hierbei gilt für den Winkel
der schiefen Ebene berechnen.
Hierbei gilt für den Winkel  :
:
(3)¶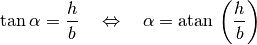
Je kleiner also der Winkel  ist, desto länger ist bei einer
bestimmten Steighöhe
ist, desto länger ist bei einer
bestimmten Steighöhe 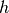 die horizontale Breite
die horizontale Breite 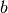 beziehungsweise
wegen
beziehungsweise
wegen 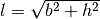 auch die Länge
auch die Länge  der schiefen Ebene.
der schiefen Ebene.
Schiefe Ebenen mit Reibung
Wird ein Gegenstand auf eine schiefe Ebene gelegt, so wird er durch die
Hangabtriebskraft 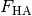 entlang der schiefen Ebene nach unten
beschleunigt. Kann die entgegengesetzt wirkende Reibungskraft zwischen dem
Objekt und der schiefen Ebene nicht vernachlässigt werden, so muss sie
folgendermaßen berücksichtigt werden:
entlang der schiefen Ebene nach unten
beschleunigt. Kann die entgegengesetzt wirkende Reibungskraft zwischen dem
Objekt und der schiefen Ebene nicht vernachlässigt werden, so muss sie
folgendermaßen berücksichtigt werden:
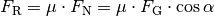
Hierbei bezeichnet 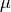 die Reibungszahl für Haft-
beziehungsweise Gleitreibung; zudem wurde für die wirkende Normalkraft
die Reibungszahl für Haft-
beziehungsweise Gleitreibung; zudem wurde für die wirkende Normalkraft
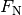 die obige Formel (1)
verwendet.
die obige Formel (1)
verwendet.
Befindet sich das Objekt auf der schiefen Ebene zunächst in Ruhe, so beginnt es dann zu gleiten, wenn die Hangabtriebskraft die maximale Haftreibungskraft übersteigt. Für den Grenzfall gilt:
![F_{\mathrm{HA}} &= F_{\mathrm{R,max}} \\[6pt]
F_{\mathrm{G}} \cdot \sin{\alpha } &= \mu _{\mathrm{H}} \cdot F_{\mathrm{G}}
\cdot \cos{\alpha } \\[4pt]](../../_images/math/4463690ee2838556eb714b1aab09f60d0f630aa4.png)
Bei dieser Gleichung kann auf beiden Seiten 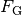 gekürzt
werden; man erhält somit:
gekürzt
werden; man erhält somit:
(4)¶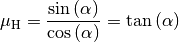
Ist die Haftreibungszahl für das Materialien-Paar (Objekt – Schiefe Ebene)
bekannt, so kann man also unmittelbar angeben, ab welchem Winkel  das Objekt anfangen wird zu rutschen:
das Objekt anfangen wird zu rutschen:
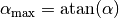
Der Winkel 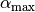 wird auch „maximaler Böschungswinkel“
genannt. Mit ihm kann beispielsweise ausgedrückt werden, bis zu welcher Steigung
ein pulverartiges Schüttgut aufgehäuft werden kann, bevor ein Nachrutschen des
Materials einsetzt.
wird auch „maximaler Böschungswinkel“
genannt. Mit ihm kann beispielsweise ausgedrückt werden, bis zu welcher Steigung
ein pulverartiges Schüttgut aufgehäuft werden kann, bevor ein Nachrutschen des
Materials einsetzt.
| Material | Winkel in Grad |
| Asche | ![\unit[40]{\degree}](../../_images/math/5a3136c6043f08ac00f373bff011d0ebd4d2c83d.png) |
| Erde | ![\unit[30]{\degree}](../../_images/math/4ea3c3bd2d01ff764d88d4bc18c22ea13e25d1b7.png) bis bis ![\unit[45]{\degree}](../../_images/math/d04f20be51133cb113d5f875c8c977c5a3323a92.png) |
| Holzrinde (klein gestückelt) | ![\unit[45]{\degree}](../../_images/math/d04f20be51133cb113d5f875c8c977c5a3323a92.png) |
| Kleie | ![\unit[30]{\degree}](../../_images/math/4ea3c3bd2d01ff764d88d4bc18c22ea13e25d1b7.png) bis bis ![\unit[45]{\degree}](../../_images/math/d04f20be51133cb113d5f875c8c977c5a3323a92.png) |
| Kies | ![\unit[45]{\degree}](../../_images/math/d04f20be51133cb113d5f875c8c977c5a3323a92.png) |
| Sand (trocken) | ![\unit[34]{\degree}](../../_images/math/56232e561cdc93883a94a969c69084bc8ccc97d2.png) |
| Sand (nass) | ![\unit[45]{\degree}](../../_images/math/d04f20be51133cb113d5f875c8c977c5a3323a92.png) |
| Schnee | ![\unit[38]{\degree}](../../_images/math/6eae634ba64351d1719a2fc1a51d2ef40277711e.png) |
Bewegt sich ein Objekt mit einer konstanten Geschwindigkeit eine schiefe Ebene
hinab, so ist die Hangabtriebskraft gleich der Gleitreibungskraft. Durch eine
experimentelle Bestimmung des zugehörigen Winkels  kann somit die
Gleitreibungszahl
kann somit die
Gleitreibungszahl 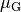 zwischen dem Material des Objekts und
dem Material der schiefen Ebene bestimmt werden.
zwischen dem Material des Objekts und
dem Material der schiefen Ebene bestimmt werden.
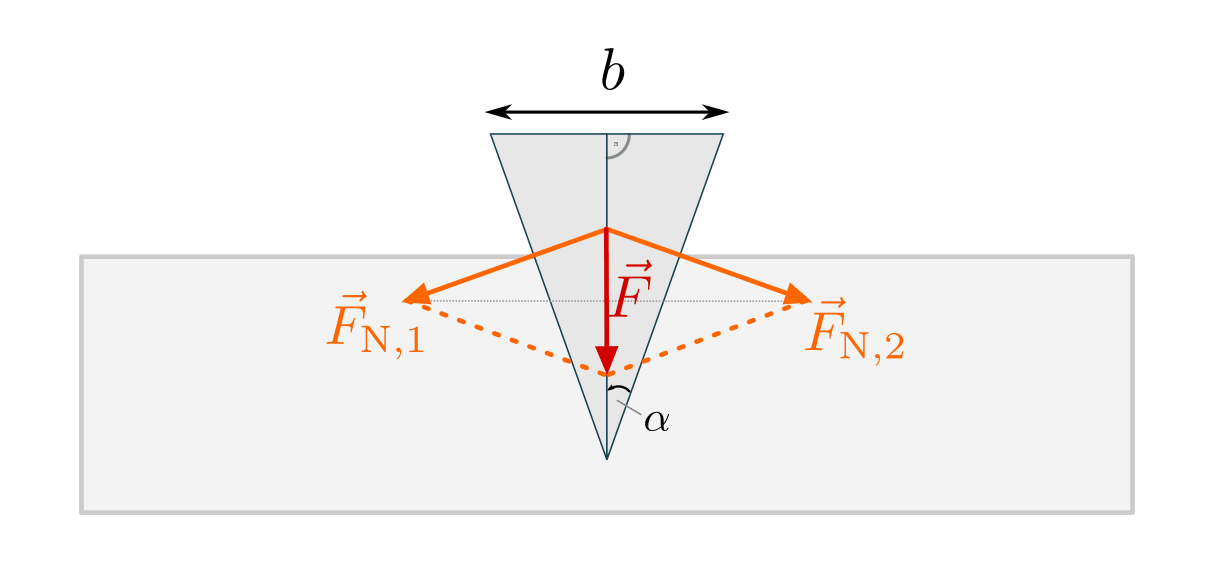
Keilwirkung
Ein Keil, auf dessen Rückseite eine Kraft  ausgeübt wird, kann das
umliegende Material auseinander treiben. Diese spaltende Wirkung, die
beispielsweise bei Äxten oder Meißeln genutzt wird, lässt sich ebenfalls mittels
der Kraftaufteilung an einer schiefen Ebene erklären, wenn man sich den Keil in
zwei rechtwinklige Dreiecke zerlegt denkt.
ausgeübt wird, kann das
umliegende Material auseinander treiben. Diese spaltende Wirkung, die
beispielsweise bei Äxten oder Meißeln genutzt wird, lässt sich ebenfalls mittels
der Kraftaufteilung an einer schiefen Ebene erklären, wenn man sich den Keil in
zwei rechtwinklige Dreiecke zerlegt denkt.
Die Kraft  , die auf den Keil ausgeübt wird, kann in zwei Normalkräfte
, die auf den Keil ausgeübt wird, kann in zwei Normalkräfte
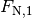 und
und 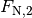 senkrecht zu den Keilflächen
zerlegt werden.
Bezeichnet man die Breite des Keilrückens mit
senkrecht zu den Keilflächen
zerlegt werden.
Bezeichnet man die Breite des Keilrückens mit 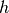 , die Länge einer
schrägen Keilflächen mit
, die Länge einer
schrägen Keilflächen mit  und den halben Keilwinkel als
und den halben Keilwinkel als  ,
so gilt:
,
so gilt:
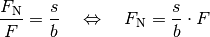
Da die Länge  der schrägen Flächen üblicherweise länger ist als
die Breite
der schrägen Flächen üblicherweise länger ist als
die Breite 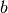 des Keils, sind die spaltenden Normalkräfte größer als
die auf den Keil wirkende Kraft
des Keils, sind die spaltenden Normalkräfte größer als
die auf den Keil wirkende Kraft  .
.
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.