Arten mechanischer Kräfte¶
Bei einer mechanischen Kraft denkt man häufig an Muskelkraft oder die Kraft eines Motors; weitere mechanische Kräfte, für die es jeweils eigene Formeln als Rechengrundlage gibt, sind im folgenden Abschnitt näher beschrieben.
Gewichtskraft¶
Die Gewichtskraft eines Objekts ist diejenige Kraft, mit der es von der Erde angezogen wird.
Je größer die Masse eines Objekts ist, desto stärker wird es von der Erde angezogen. Bei einer größeren Masse ist allerdings auch eine größere Kraft nötig, um sie zu beschleunigen; ohne Luftwiderstand werden daher alle Objekte, die sich im freien Fall befinden, gleich schnell zum Erdmittelpunkt hin beschleunigt.
Formel:
Auf der Erdoberfläche gilt für den Ortsfaktor, wie sich aus dem allgemeinen
Gravitationsgesetz ableiten lässt, näherungsweise ![g = |\vec{g}| =
\unit[9,81]{\frac{N}{kg}}](../../_images/math/67633ad44bdad16fb3dd2bc6269f54aa4bdccb1c.png) .[2]
.[2]
Beispiele:
Ein Objekt mit einer Masse von
![\unit[1,0]{kg}](../../_images/math/4bfaeba06ae2abb8f90814c1482851633c72309c.png) hat auf der Erde eine
Gewichtskraft von
hat auf der Erde eine
Gewichtskraft von![F_{\mathrm{G, Erde}} = m \cdot g = \unit[1]{kg} \cdot
\unit[9,81]{\frac{N}{kg}} = \unit[9,81]{N}](../../_images/math/8100045ea461441fa5b2b39a451b4a256e7a866d.png)
Ein Objekt mit einer Masse von
![\unit[50]{kg}](../../_images/math/ace271226a971d2a199f66cd92cc0e82f4d9675c.png) hat auf der Erde eine
Gewichtskraft von
hat auf der Erde eine
Gewichtskraft von![F_{\mathrm{G, Erde}} = \unit[50]{kg} \cdot \unit[9,81]{\frac{N}{kg}} =
\unit[490,5]{N}](../../_images/math/b289e62c8bb5ff6647f9386d568360417ba88ada.png)
Das Gewicht eines Objekts ist nicht an allen Stellen auf der Erde exakt gleich, sondern hängt vom Ort ab, an dem es sich befindet:
- Auf einem hohen Berg hat ein Objekt ein etwas geringeres Gewicht als in Höhe des Meeresspiegels.
- An verschiedenen Stellen der Erde hat jedes Objekt – da die Erde keine ideale Kugelgestalt hat, sondern zu den Polen hin etwas „abgeflacht“ ist – ebenfalls ein geringfügig unterschiedliches Gewicht. Im Vergleich zu Mitteleuropa ist ein Objekt am Äquator etwas leichter, an den Polen etwas schwerer.
- Auf dem Mond oder auf anderen Planeten hängt die Gewichtskraft, die ein Objekt erfährt, von der Masse des jeweiligen Himmelskörpers ab: Je schwerer ein Planet ist, desto größer ist die Anziehungskraft, die er auf andere Massen ausübt.
| Ort | Ortsfaktor in ![\unit[]{\frac{N}{kg}}](../../_images/math/c659f74c4233ab9975a7c26935febc74cd5f41ee.png) |
| Äquator | 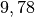 |
| Mitteleuropa | 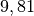 |
| Pole der Erde | 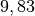 |
![\unit[300]{km}](../../_images/math/542e8ce6294170a038987ea944e5b44695842ba0.png) über der Erde über der Erde |
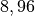 |
![\unit[40\, 000]{km}](../../_images/math/489ab952d0bc8eb6f35bf97b90365a792f5080ff.png) über der Erde über der Erde |
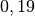 |
| Mond der Erde | 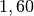 |
| Venus | 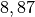 |
| Mars | 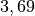 |
| Merkur | 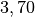 |
| Jupiter | 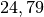 |
| Saturn | 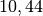 |
| Sonne | 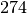 |
Auf dem Mond hat ein Objekt der Masse ![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) eine
Gewichtskraft von
eine
Gewichtskraft von
![F_{\mathrm{G, Mond}} = \unit[1]{kg} \cdot
\unit[1,62]{\frac{N}{kg}} = \unit[1,62]{N}](../../_images/math/498192fa15aab6066735cf9776484eb05e27376c.png)
Auf der Sonne erfährt ein Objekt der Masse ![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) eine
Gewichtskraft von
eine
Gewichtskraft von
![F_{\mathrm{G, Sonne}} = \unit[1]{kg} \cdot \unit[274]{\frac{N}{kg}} =
\unit[274]{N}](../../_images/math/e5c6587e4d84a2a43ef5e92a2219058ba50cc069.png)
Im Universum haben Objekte also überall die gleiche Masse, jedoch nicht das gleiche Gewicht.
Reibungskraft¶
Erfahrungsgemäß kommt jedes bewegte Objekt, das nicht angetrieben wird, nach
einer gewissen Zeit zur Ruhe. Da seine Geschwindigkeit abnimmt, muss eine
bremsende Kraft wirken. Eine derartige Kraft nennt man Reibungskraft
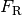 .
.
Reibungskräfte treten immer auf, wenn sich Objekte berühren und gegeneinander bewegen. Ursache dafür sind die unebenen Oberflächen der Objekte und Kohäsionskräfte, die zwischen den Molekülen der aneinander reibenden Objekte wirken.
Haftreibung
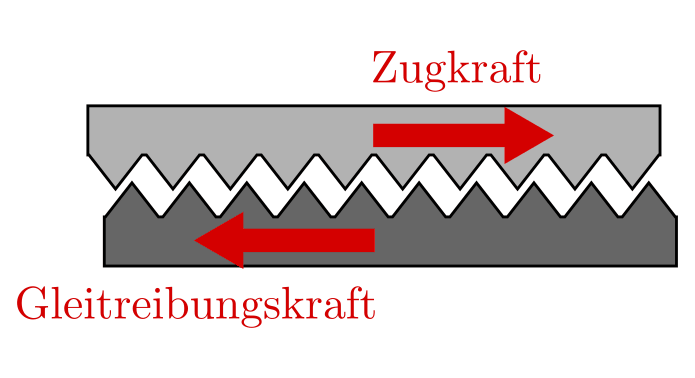
Bei starker Vergrößerung gleicht selbst eine geschliffene Oberfläche einem kleinen Gebirge mit vielen Zacken und Spitzen. Haften zwei Objekte aneinander, so verhaken sich diese Spitzen ineinander. Versucht man die Objekte gegeneinander zu bewegen, so werden die Zacken etwas verformt; einer stärkeren Zugkraft wirkt eine stärkere Haftreibungskraft entgegen.
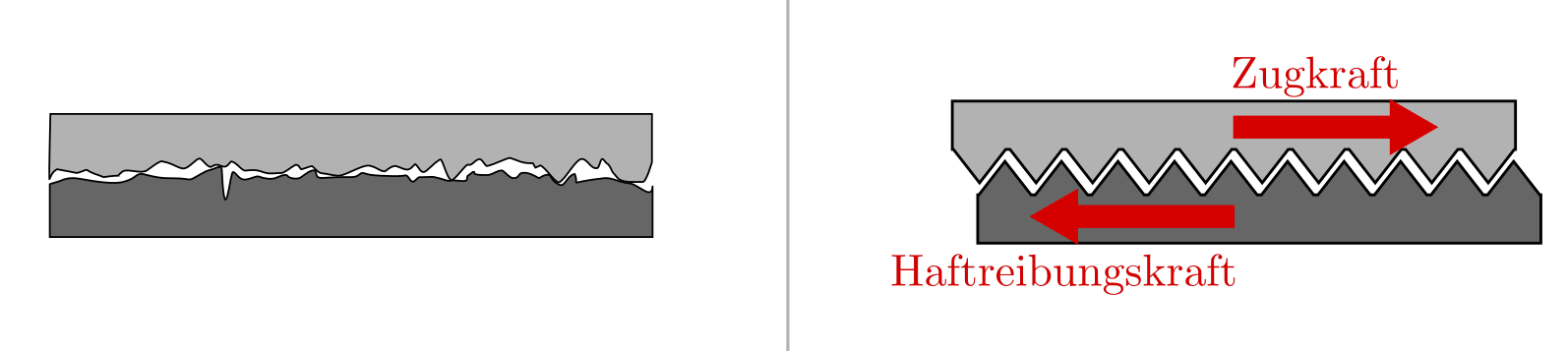
Stark vergrößerte Darstellung der Oberfläche von gleitenden Körpern und Modelldarstellung der Haftreibung.
Je stärker zwei Objekte aneinander gepresst sind, desto stärker ist die maximale Haftreibungskraft (als anschauliches Beispiel kann man zwei Bürsten ineinander stecken und versuchen sie gegeneinander zu bewegen).
Formel:
Haften zwei Objekte aneinander, so ist der Betrag der maximalen Haftreibungskraft
proportional zu der Normalkraft
, die beide Körper aneinander presst:
Die Proportionalitätskonstante heißt Haftreibungszahl 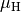 und hängt vom Stoff und von der Oberflächenbeschaffenheit der Objekte ab. Ist
die angreifende Kraft größer als die maximale Haftreibungskraft, so beginnen die
Objekte relativ zueinander zu gleiten.
und hängt vom Stoff und von der Oberflächenbeschaffenheit der Objekte ab. Ist
die angreifende Kraft größer als die maximale Haftreibungskraft, so beginnen die
Objekte relativ zueinander zu gleiten.
| Stoffpaar | Haftreibungszahl 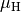 |
Gleitreibungszahl 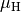 |
| Holz auf Holz | 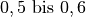 |
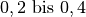 |
| Stahl auf Stahl | 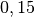 |
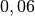 |
| Stahl auf Eis | 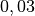 |
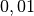 |
| Autoreifen auf Beton (trocken) | 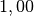 |
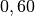 |
| Autoreifen auf Beton (nass) | 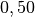 |
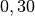 |
| Autoreifen auf Eis | 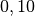 |
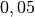 |
Gleitreibung
Bewegen sich zwei Objekte gegeneinander, so schlittern die rauhen Oberflächen übereinander hinweg. Sie können sich – anders als bei der Haftreibung – nicht völlig ineinander verhaken.
Formel:
Die Gleitreibungskraft
hängt – wie auch die Haftreibungskraft – von der zusammenpressenden Gewichts- oder Normalkraft
und der Oberflächenbeschaffenheit der Objekte ab:
Die Gleitreibungszahl 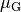 ist stets kleiner als die
Haftreibungszahl
ist stets kleiner als die
Haftreibungszahl 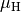 .
.
Rollreibung
Rollt ein Objekt auf dem anderen entlang, so können die Unebenheiten der Oberflächen deutlich leichter überwunden werden. Die Rollreibungskraft ist bei gleicher zusammenpressender (Gewichts-)Kraft wesentlich kleiner als die Gleitreibungskraft.
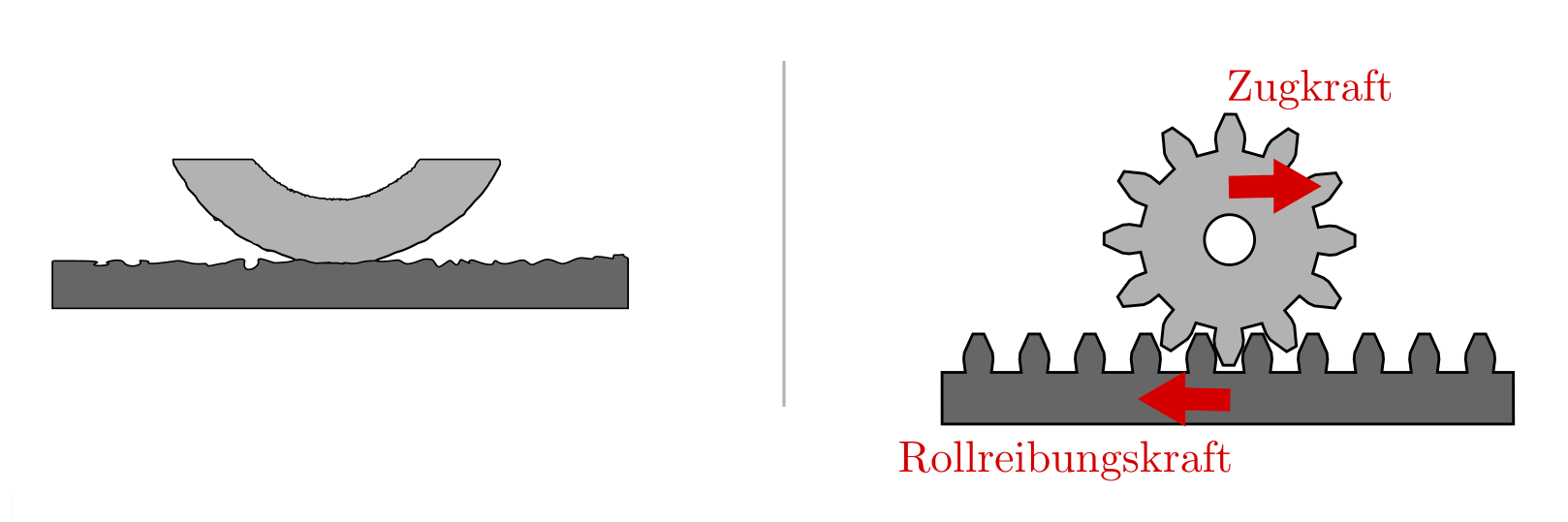
Stark vergrößerte Darstellung eines auf einer Unterlage abrollenden Rades und Modellvorstellung der Rollreibung.
Um unerwünschte Reibungskräfte zu verringern, verwendet man Schmiermittel (Fett, Öl). Dadurch wird der Raum zwischen den sich reibenden Flächen ausgefüllt, so dass sich die Unebenheiten der Körper nicht mehr so störend auswirken.
| Stoffpaar | Rollreibungszahl 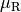 |
| Eisen auf Eisen | 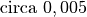 |
| Kugeln im Kugellager | 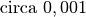 |
In sehr vielen Fällen sind Reibungskräfte allerdings unterlässlich: Ohne Reibungskräfte zwischen den Rädern von Fahrzeugen und der Straße wäre eine gezielte Fortbewegung unmöglich: Die Räder würden durchdrehen. Um ihnen vielmehr eine möglichst gute Straßenlage zu geben, werden die Reifen aus Spezialgummi gefertigt und mit Profilen versehen. Ohne Reibung wären auch Bremsen oder gar Klebstoffe unmöglich.
Strömungswiderstand
Bewegt sich ein Objekt durch ein flüssiges oder gasförmiges Medium, so muss es
stets einen Strömungswiderstand (beispielsweise Luftwiderstand) überwinden.
Hierbei hängt die Größe der Widerstandskraft von der Dichte 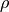 des
durchquerten Mediums, der Querschnittsfläche
des
durchquerten Mediums, der Querschnittsfläche  des Körpers, dem Quadrat
seiner Geschwindigkeit
des Körpers, dem Quadrat
seiner Geschwindigkeit 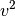 sowie einem so genannten „Widerstandsbeiwert“
sowie einem so genannten „Widerstandsbeiwert“
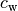 ab; letzterer gibt den Einfluss der Objektform an.
ab; letzterer gibt den Einfluss der Objektform an.
Beispielsweise gilt für die Luftwiderstandskraft 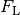 näherungsweise folgende Formel:[3]
näherungsweise folgende Formel:[3]
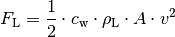
Bei üblichen Straßenfahrzeugen kann der Widerstandsbeiwert im optimalen Falle
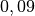 betragen, bei Omnibusssen sind Werte bis zu
betragen, bei Omnibusssen sind Werte bis zu 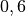 üblich.
üblich.
| Gegenstand | 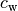 -Wert -Wert |
| Halbkugel (konkav), Fallschirm | 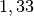 |
| Rechteckige Platte | 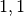 bis bis 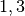 |
| Kreisförmige Platte | 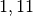 |
| Mensch (stehend) | 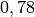 |
| LKW | 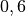 bis bis 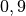 |
| Fahrradfahrer (Mountainbike) | 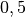 bis bis 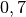 |
| Kugel | 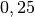 bis bis 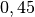 |
| Halbkugel (konvex) | 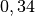 |
| Tropfen (Stromlinienform) | 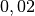 |
Die Dichte der Luft beträgt unter Normalbedingungen ![\rho_{\mathrm{Luft}} =
\unit[1,29]{kg/m^3}](../../_images/math/a075e8e5d678d88ce091985e4dba84f72b78bcc9.png) . Für die Berechnung der Wasserwiderstandkraft muss mit der
entsprechend höheren Dichte von Wasser
. Für die Berechnung der Wasserwiderstandkraft muss mit der
entsprechend höheren Dichte von Wasser ![(\rho_{\mathrm{Wasser}} =
\unit[1000]{kg/m^3})](../../_images/math/b5aaaf833e5dd7cb34943183ddab61486477dad4.png) gerechnet werden.
gerechnet werden.
Spannkraft¶
Drückt man einen elastischen Gegenstand, beispielsweise eine Schraubenfeder, zusammen oder zieht ihn auseinander, so wirkt in ihm eine entgegengesetzt gerichtete Kraft, die ihn wieder auf ihre ursprüngliche Länge zurück zu formen versucht.
Formel:
Je weiter die Wegstreckeist, um die eine Schraubenfeder gestaucht oder gedehnt wird, desto stärker ist die rückstellende Spannkraft
der Feder.
(2)¶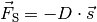
Die Federkonstante 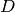 ist dabei von der Form und dem Material der Feder
beziehungsweise des elastischen Körpers abhängig. Die Federkonstante (und damit
die Federhärte) einer Schraubenfeder ist beispielsweise umso größer, je dicker
der Draht ist und je enger er gewickelt ist; sie wird im Allgemeinen in Newton
je Meter
ist dabei von der Form und dem Material der Feder
beziehungsweise des elastischen Körpers abhängig. Die Federkonstante (und damit
die Federhärte) einer Schraubenfeder ist beispielsweise umso größer, je dicker
der Draht ist und je enger er gewickelt ist; sie wird im Allgemeinen in Newton
je Meter 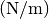 angegeben.
angegeben.
Das Minuszeichen in Gleichung (2) bedeutet, dass die Richtung der
Auslenkung der Feder  von ihrer Ruhelage der Richtung der Federkraft
entgegengesetzt ist. Gleichung (2) wird zu Ehren ihres
Entdeckers, Robert Hooke, auch
als „Hookesches Gesetz“ bezeichnet.
von ihrer Ruhelage der Richtung der Federkraft
entgegengesetzt ist. Gleichung (2) wird zu Ehren ihres
Entdeckers, Robert Hooke, auch
als „Hookesches Gesetz“ bezeichnet.
Radialkraft¶
Ein Körper bewegt sich aufgrund seiner Masse stets entlang einer geradlinigen Bahn, wenn keine Kraft auf ihn einwirkt. Eine kreisförmige Bewegung ist somit nur möglich, wenn eine Kraft den Körper auf der Kreisbahn hält, also ihn kontinuierlich zum Kreismittelpunkt hin beschleunigt. Diese Kraft wird Radialkraft beziehungsweise Zentripetalkraft genannt.
Für den Betrag der Radialkraft gilt ebenfalls das Kraftgesetz 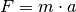 . Mit der Radialbeschleunigung
. Mit der Radialbeschleunigung 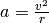 folgt für die Radialkraft
folgt für die Radialkraft
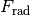 :
:
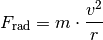
Befindet man sich als Beobachter selbst auf einer Kreisbahn, so nimmt man hingegen die entsprechende Gegenkraft („Zentrifugalkraft“) wahr. Sitzt man beispielsweise in einem Fahrzeug, das nach links lenkt, so scheint eine Kraft zu wirken, die den eigenen Körper zur rechten Seite hin beschleunigt (Scheinkraft). In Wirklichkeit versucht man sich aufgrund der Trägheit geradeaus zu bewegen und wird erst durch die zum Kreismittelpunkt hin wirkende Radialkraft auf die Kreisbahn gezwungen.
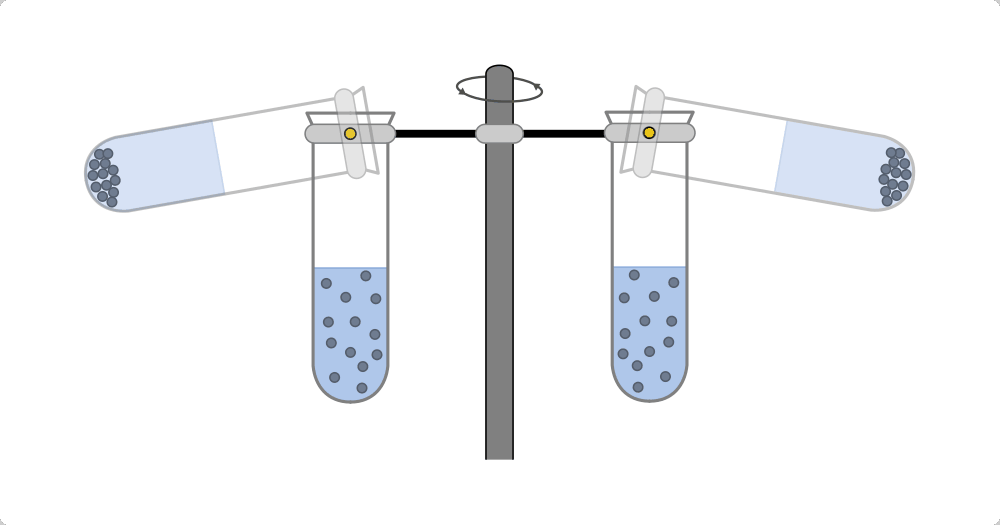
Technisch wird die Radialkraft beispielsweise in Zentrifugen genutzt. Dabei wird
ein zu trennendes Gemisch an Substanzen, die sich beispielsweise in einem
Reagenzglas befinden, in eine Kreisbewegung mit hoher Winkelgeschwindigkeit und
kleinem Bahnradius versetzt. Das Stoffgemisch wird dabei gemäß seiner
Dichte-Anteile aufgetrennt, die „schwereren“ Substanzen bewegen sich dabei
aufgrund ihrer Trägheit nach außen und lagern sich so am Boden des rotierenden
Gefäßes ab. Diese Schichtung bleibt auch nach einem Abschalten der Zentrifuge
bestehen, da letztlich nichts anderes als ein Sedimentationsvorgang
stattgefunden hat – nur ein sehr schneller. Die durch die Radialkraft bewirkte
Radialbeschleunigung kann mit Zentrifugen beziehungsweise Ultrazentrifugen ein
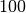 - bis
- bis 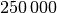 -faches der Erdbeschleunigung
-faches der Erdbeschleunigung 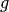 betragen.
betragen.
Anmerkungen:
| [1] | Der Ortsfaktor
Der Ortsfaktor kann somit einerseits als Beschleunigungs-Wert aufgefasst
werden (wenn sich ein Objekt im freien Fall befindet) als auch als
Umrechnungsfaktor zwischen der Masse |
| [2] | Genau genommen ist die obige Formel eine Näherung für das allgemeine
Gravitationsgesetz, wonach auf zwei Körper mit den Massen Dabei ist
Für die Gewichtskraft eines Körpers
|
| [3] | Bei turbulenten Strömungen mit komplexen Luftverwirbelungen lässt sich der Luftwiderstand nicht mit Hilfe einer einzelnen Formel berechnen, sondern erfordert aufwendige Computer-Simulationen und numerische Verfahren. Die Formel |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

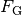 , die ein Objekt der Masse
, die ein Objekt der Masse
 durch die Anziehungskraft eines Planeten erfährt, ist proportional
zum so genannten Ortsfaktor
durch die Anziehungskraft eines Planeten erfährt, ist proportional
zum so genannten Ortsfaktor 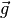 :
: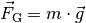
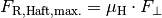
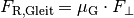
![g = \unit[9,81]{\frac{N}{kg}} =
\unit[9,81]{\frac{m}{s^2}}](../../_images/math/d8a0e8ee0d188c13db79ad4cea7689bd35c6882d.png) wird bisweilen auch als
wird bisweilen auch als 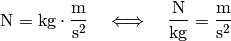
![\unit[1]{kg} \stackrel{\wedge}=
\unit[9,81]{N}](../../_images/math/dfcaee9b9eadf19885fd9a1070b34b22eeca778c.png) .
.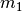 und
und
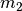 stets eine anziehende Kraft
stets eine anziehende Kraft  zwischen ihren
Schwerpunkten abhängig:
zwischen ihren
Schwerpunkten abhängig: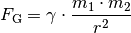
![\gamma = \unit[6,67 \cdot 10^{-11}]{\frac{m^3}{kg \cdot
s^2}}](../../_images/math/d51bc14c9035c850cbfa93cab9e4e2c5aacab7ac.png) die allgemeine Gravitationskonstante. Für die Gewichtskraft, die ein
Körper in Nähe der Erdoberfläche erfährt, kann näherungsweise und
die allgemeine Gravitationskonstante. Für die Gewichtskraft, die ein
Körper in Nähe der Erdoberfläche erfährt, kann näherungsweise und ![r
\approx r_{\mathrm{E}} = \unit[6371]{km}](../../_images/math/bc5501541e89b6264d13ebcc562391bf590c6942.png) gesetzt werden (der Abstand eines
Gegenstands von der Erdoberfläche ist meist vernachlässigbar klein gegenüber
dem Erdradius). Mit der Erdmasse
gesetzt werden (der Abstand eines
Gegenstands von der Erdoberfläche ist meist vernachlässigbar klein gegenüber
dem Erdradius). Mit der Erdmasse ![m_{\mathrm{E}} = \unit[5,972 \cdot
10^{24}]{kg}](../../_images/math/ca9b40c43404a7e1247ea34922bd79c331b7fa6f.png) kann der Ortsfaktor
kann der Ortsfaktor ![g = \gamma \cdot \frac{m_{\mathrm{E}}}{r_{\mathrm{E}}^2} \, \approx \, \unit[9,81]{\frac{m}{s^2}}](../../_images/math/9f439034d2480e09610537bada19d432b2a42af1.png)
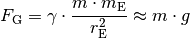
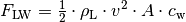 lässt sich aus dem Zusammenhang
lässt sich aus dem Zusammenhang
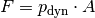 zwischen Kraft,
zwischen Kraft,