Zusammenwirken mehrerer Kräfte¶
Wirken mehrere Kräfte auf einen Körper ein, so kann man sich diese als zu einer
Gesamtkraft zusammengesetzt denken. Die Gesamtkraft 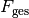 hat
auf den Körper die gleiche Wirkung wie die gemeinsame Wirkung der
hat
auf den Körper die gleiche Wirkung wie die gemeinsame Wirkung der  einzelnen (Teil-)Kräfte.
einzelnen (Teil-)Kräfte.
(1)¶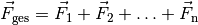
Will man die Wirkung mehrerer Kräfte auf einen Körper angeben, müssen Betrag und Richtung jeder Kraft bekannt sein.
Zusammenwirken mehrerer Kräfte mit gleicher Richtung¶
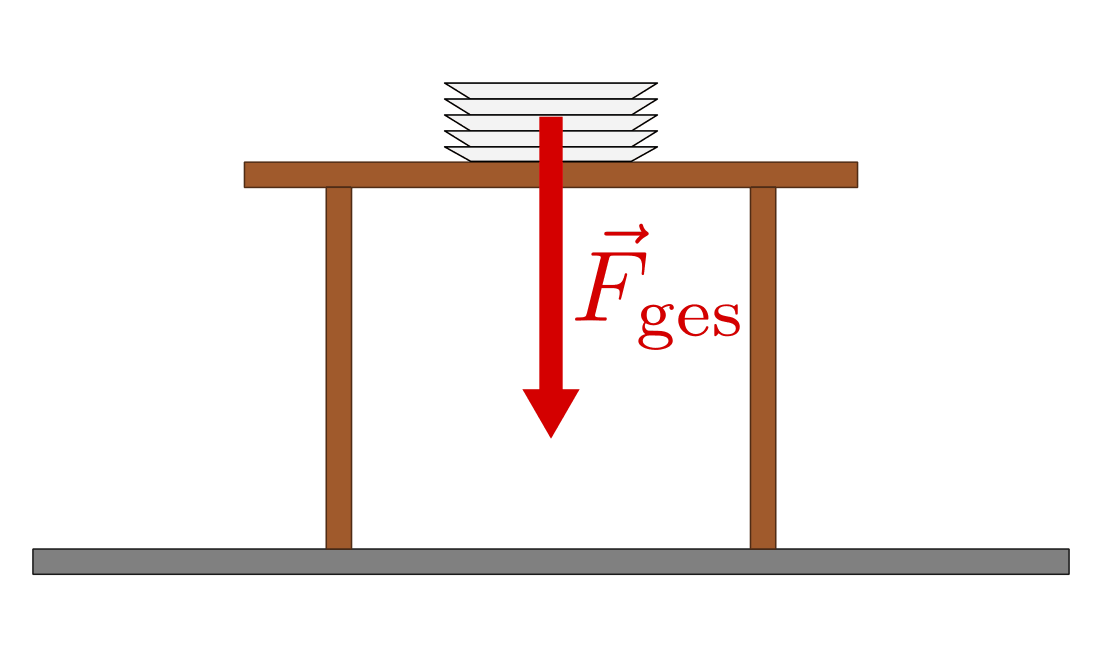
Wirken zwei Teilkräfte in die gleiche Richtung, so erhält man die Gesamtkraft, indem man die Beträge der Teilkräfte addiert. Die Gesamtkraft zeigt in die gleiche Richtung wie die einzelnen Teilkräfte.
Beispiel:
- Die Gewichtskraft, die ein Stapel Teller auf eine Unterlage ausübt, ist gleich der Summe der Gewichtskräfte der einzelnen Teller.
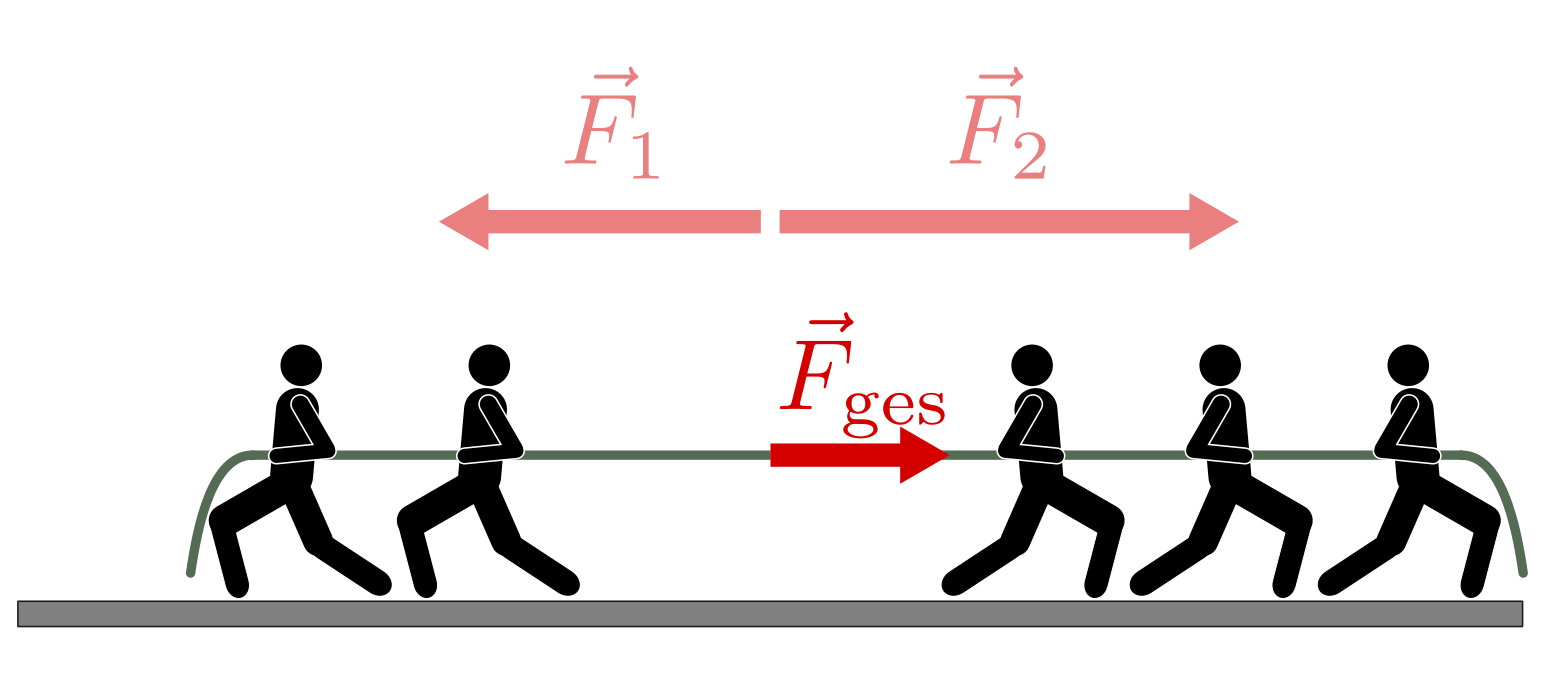
Wirken zwei Teilkräfte in die entgegengesetzte Richtung, so erhält man die Gesamtkraft, indem man die Differenz aus den Beträgen der Teilkräfte bildet. Die Gesamtkraft zeigt in Richtung der größeren der beiden Teilkräfte.
Beispiel:
- Zieht beim Seilziehen eine Gruppe stärker als die andere, so bewegen sich alle Teilnehmer in die Richtung der stärkeren Kraft. Die Gesamtkraft, mit der alle Teilnehmer beschleunigt werden, ist gleich dem Kraftunterschied beider Gruppen. (Ziehen beide Gruppen gleich stark, so sind beide Kräfte im Gleichgewicht, und kein Körper wird beschleunigt.)
Zusammenwirken mehrerer Kräfte mit unterschiedlicher Richtung¶
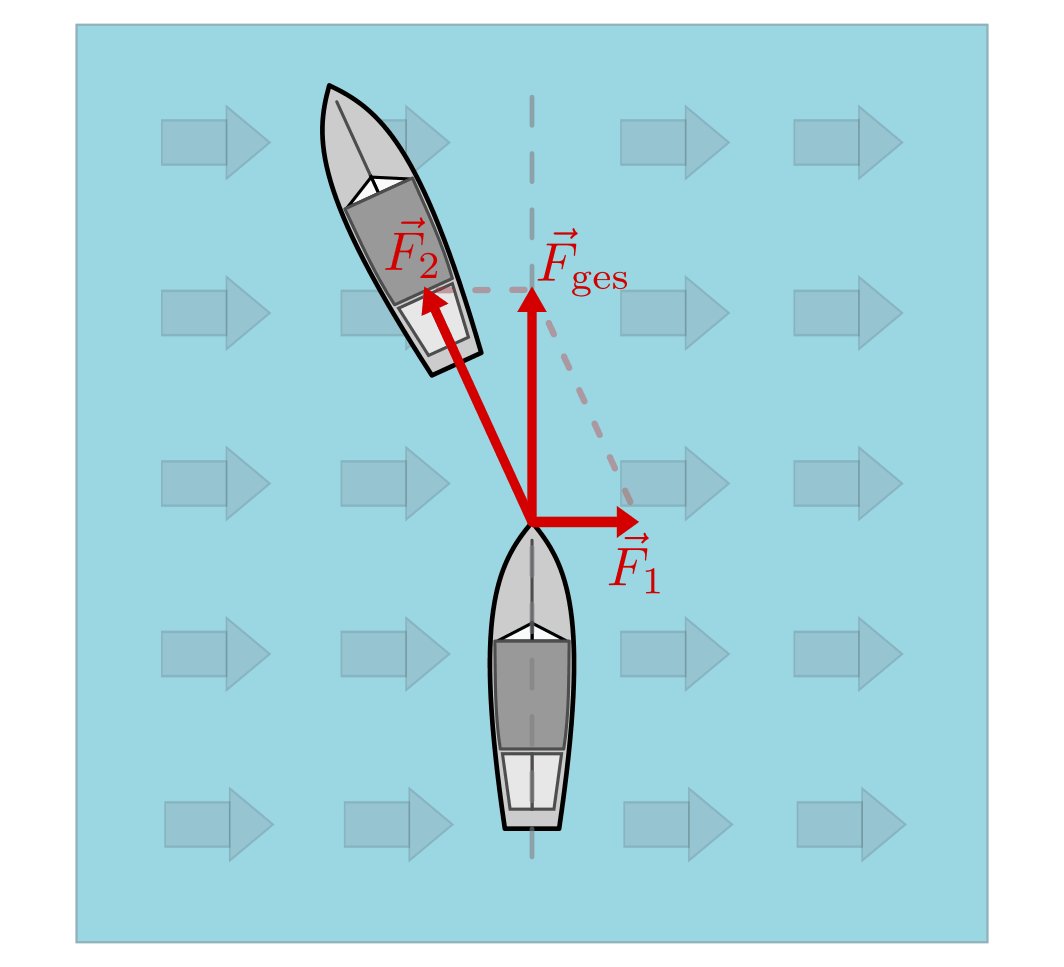
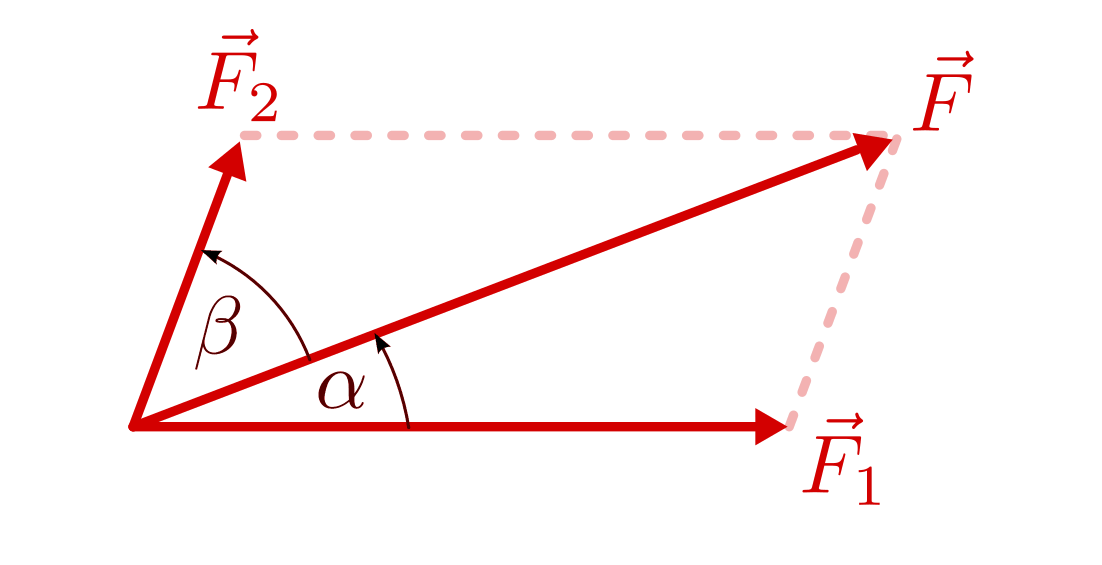
Wirken an einem Punkt mehrere Kräfte in unterschiedlicher Richtung, so sind für die Bestimmung der resultierenden Kraft die Beträge wie auch die Richtungen der einzelnen Teilkräfte zu berücksichtigen. In Zeichnungen lassen sich die wirkenden Teilkräfte wiederum als Vektorpfeile darstellen; dabei müssen die Längen der Vektoren zueinander in einem frei wählbaren Maßstab den Beträgen der einzelnen Kräfte entsprechen.
Beispiel:
- Soll ein Schiff von einem anderen ohne Abdrift über einen Fluss gezogen werden, so muss die Kraft des ziehenden Schiffes auch die Schubkraft des fließenden Wassers ausgleichen.
Die sich aus zwei Teilkräften ergebende Gesamtkraft kann zeichnerisch ermittelt werden, indem beide Vektorpfeile addiert werden, d.h. der Anfangspunkt des einen Vektors an die Spitze des anderen Vektors verschoben wird. Die Verbindungslinie vom gemeinsamen Angriffspunkt zum sich so ergebenden Endpunkt entspricht dann der resultierenden Gesamtkraft.[1]
Rechnerisch erhält man die sich aus zwei Teilkräften 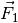 und
und 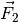 ergebende Gesamtkraft
ergebende Gesamtkraft 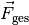 ,
indem man die einzelnen Komponenten beider Kraftvektoren miteinander addiert:
,
indem man die einzelnen Komponenten beider Kraftvektoren miteinander addiert:
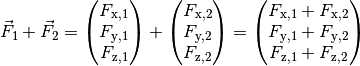
Der Betrag der wirkenden Gesamtkraft ist auch hierbei gleich dem Betrag des Ergebnisvektors, der sich gemäß folgender Formel berechnen lässt:
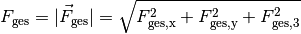
Zerlegung einer Kraft in Teilkräfte¶
In gleicher Art und Weise, wie sich mehrere Kräfte zu einer Gesamtkraft addieren lassen, kann man eine Kraft auch in mehrere Teilkräfte aufteilen, die gemeinsam eine gleiche Wirkung hervorrufen.
Beispiel:
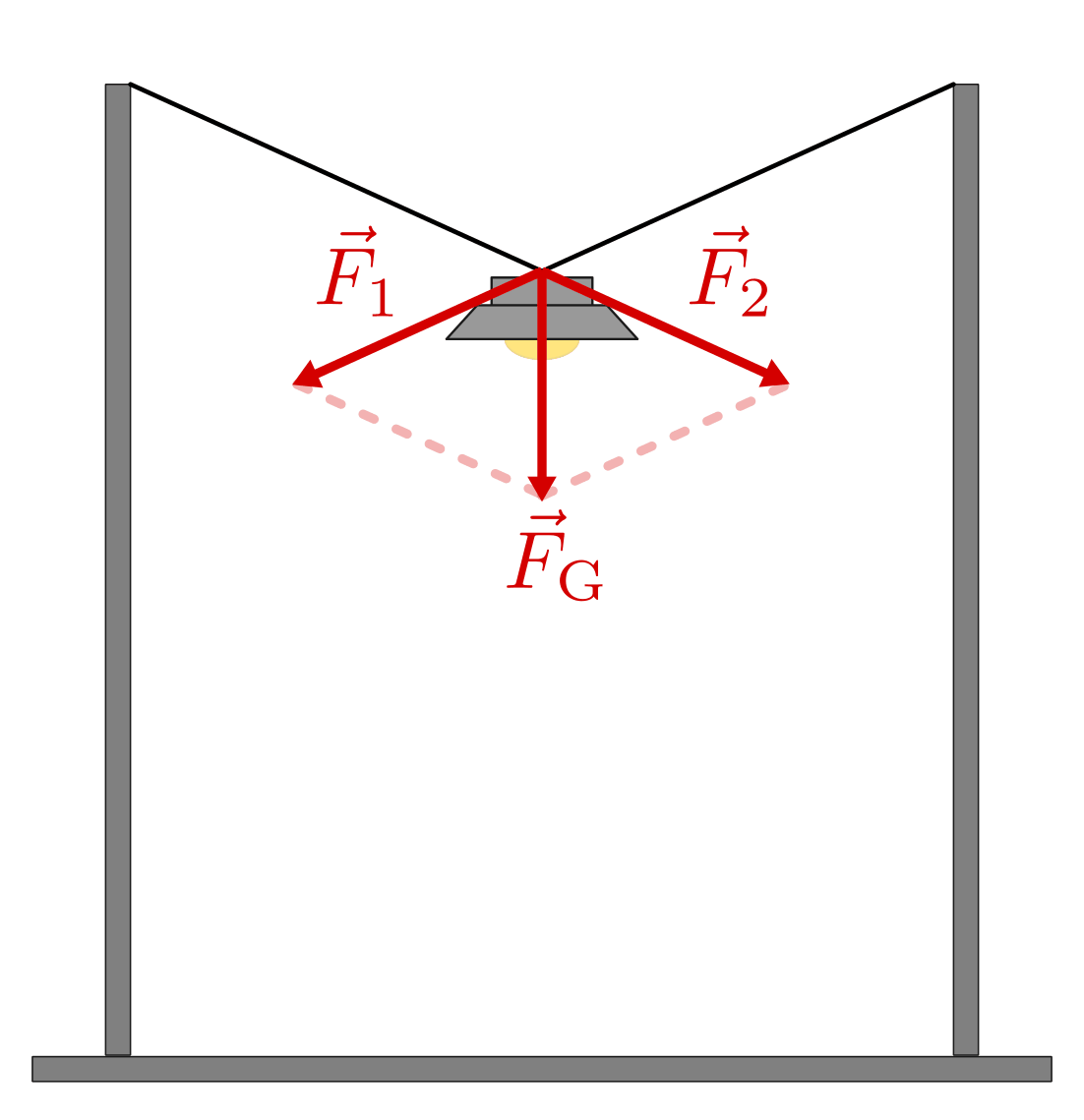
- Eine Straßenlampe wird von zwei Halteseilen getragen. Diese können nur
Zugkräfte vermitteln, d.h. die Teilkräfte
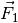 und
und
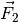 in den Seilen müssen entlang der Seilrichtungen
verlaufen; die Summe beider Teilkräfte wiederum muss der Gewichtskraft
in den Seilen müssen entlang der Seilrichtungen
verlaufen; die Summe beider Teilkräfte wiederum muss der Gewichtskraft
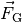 der Lampe entsprechen.
der Lampe entsprechen.
Um eine Kraft in zwei gegebene Richtungen zu zerlegen, zeichnet man vom Anfangs-
und Endpunkt der Kraft Parallelen zu diesen Richtungen. Das entstehende
Parallelogramm ergibt die gesuchten Teilkräfte 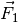 und
und
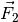 .
.
Kennt man die Winkel  und
und 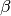 zwischen der zu
zerlegenden Kraft
zwischen der zu
zerlegenden Kraft 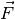 und den beiden Teilkräften
und den beiden Teilkräften 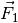 und
und 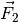 , so gilt für die Beträge
, so gilt für die Beträge 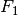 und
und 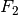 der
Teilkräfte:
der
Teilkräfte:
![F_1 = F \cdot \frac{\sin{(\beta)}}{\sin{(\alpha + \beta)}} \\[6pt]
F_2 = F \cdot \frac{\sin{(\alpha)}}{\sin{(\alpha + \beta)}} \\[6pt]](../../_images/math/e90bf8dbf7abefe222c03d1099ac98cd44e8f4b0.png)
Betragsmäßig ist die Summe 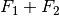 der Teilkraftbeträge, sofern die
Winkel
der Teilkraftbeträge, sofern die
Winkel  bzw.
bzw. 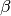 nicht gleich Null sind, stets größer
als der Betrag
nicht gleich Null sind, stets größer
als der Betrag  der zu zerlegenden Kraft.
der zu zerlegenden Kraft.
Anmerkungen:
| [1] | Wirken an einem gemeinsamen Angriffspunkt mehr als zwei Kräfte in unterschiedliche Richtungen, so kann die resultierende Gesamtkraft graphisch ermittelt werden, indem alle Vektorpfeile durch paralleles Verschieben so miteinander verbunden werden, dass der Anfangspunkt des zweiten Vektors am Endpunkt des ersten liegt, der Anfangspunkt des dritten Vektors am Endpunkt des zweiten liegt, usw. Der Vektor vom Anfangspunkt der Vektorkette zu ihrem Endpunkt entspricht der wirkenden Gesamtkraft. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.