Mechanische Kräfte¶
Kräfte erkennt man an den Wirkungen, die sie hervorrufen. Wird ein Körper verformt oder ändert sich seine Geschwindigkeit, so ist stets eine Kraft die Ursache dafür. Es können jedoch auch Kräfte wirken, ohne dass sich der Bewegungszustand eines Körpers ändert oder er (sichtbar) verformt wird. In diesem Fall heben sich mehrere gleichzeitig wirkende Kräfte in ihrer Wirkung auf („Zusammenwirken mehrerer Kräfte“).
Beim Bogenschießen wird die Sehne gespannt und dabei der Bogen elastisch verformt. Lässt man die Sehne los, so beschleunigt die Spannkraft des Bogens den Pfeil.
Die Newtonschen Gesetze¶
Die drei im folgenden kurz dargestellten Gesetzmäßigkeiten stellen die Basis der klassischen Mechanik dar. Sie wurden in dieser Form erstmals im Jahre 1687 von Isaac Newton niedergeschrieben.
Das 1. Newtonsche Gesetz („Trägheitsgesetz“)
Zur Änderung eines Bewegungszustands, d.h. zu einer Beschleunigung, ist stets eine Kraft nötig. Die Ursache dafür liegt in der sogenannten „Trägheit“, einer Eigenschaft eines jeden Körpers, sich aufgrund seiner Masse einer Beschleunigung zu widersetzen. Ursprünglich hatten Galileo Galilei und Isaac Newton diese Gesetzmäßigkeit etwa so formuliert:
„Jeder Körper verharrt im Zustand der Ruhe oder der gleichförmigen Bewegung, solange keine äußeren Kräfte an ihm wirken.“[1]
Wenn sich ein Körper mit einer festen Geschwindigkeit geradlinig bewegt, dann bleibt der Betrag und die Richtung der Bewegung konstant, bis eine Kraft eine Änderung seiner Bewegung bewirkt. Dass wir es im Alltag gewohnt sind, dass Gegenstände ohne beschleunigend wirkende Kräfte irgendwann von selbst zu Ruhe kommen, liegt an nie völlig vermeidbaren Reibungskräften und am Luftwiderstand. Im Weltall allerdings, in dem es aufgrund der Abwesenheit von Materie auch keine Reibung gibt, umkreisen die Planeten viele Millionen Jahre lang ihre Sonne(n), ohne ihre Geschwindigkeit zu verlieren.
Auch das Abbremsen eines Körpers entspricht einer (negativen) Beschleunigung und erfordert dementsprechend eine Kraft.
Das 2. Newtonsche Gesetz („Kraftgesetz“)
Als Kraft wird allgemein die Ursache einer Beschleunigung oder Verformung bezeichnet. Der quantitative Zusammenhang zwischen der Größe einer Kraft und der durch sie bewirkten Beschleunigung wurde erstmals durch Isaac Newton in Form einer mathematischen Gleichung beschreiben.
Formel:
Einheit:
Kräfte werden in der Einheit Newton
angegeben:
Beispiele:
Durch eine Kraft von
![\unit[1]{N}](../../_images/math/d4bc2af6cd73b1a3c5f1086f5f01daf958c78dac.png) erfährt ein Körper der Masse
erfährt ein Körper der Masse
![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) eine Beschleunigung von
eine Beschleunigung von ![\unit[1]{\frac{m}{s^2} }](../../_images/math/84563429e5d409828972a20be1a2698e1a652ac5.png) .
.Dies gilt im Weltall, im Vakuum, und allgemein immer dann, wenn keine Reibung auftritt. Durch Reibungskräfte kann die tatsächliche Beschleunigung in der Praxis deutlich geringer sein.
![\unit[1]{N}](../../_images/math/d4bc2af6cd73b1a3c5f1086f5f01daf958c78dac.png) entspricht auf der Erde der Gewichtskraft eines
entspricht auf der Erde der Gewichtskraft eines
![\unit[100]{g}](../../_images/math/b25c7db38f69092eb13d4bb9ac59285044dfbd1c.png) schweren Körpers.
schweren Körpers.Eine Masse von
![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) erfährt auf der Erde eine
Gewichtskraft von rund
erfährt auf der Erde eine
Gewichtskraft von rund ![\unit[10]{N}](../../_images/math/427f119ae47b073818745b78efd9146babe643e9.png) . Im freien Fall übt die Erde
damit eine Beschleunigung von rund
. Im freien Fall übt die Erde
damit eine Beschleunigung von rund ![\unit[10]{\frac{m}{s^2}}](../../_images/math/8e6acec8fcf4de062bc937ac872204aa60559f24.png) (genauer:
(genauer: ![\unit[9,81]{\frac{m}{s^2}}](../../_images/math/c5f7ef8df878a11d9fdee758fd171ba206258304.png) ) auf sie aus.
) auf sie aus.
Kräfte werden nach ihrer Ursache (Muskelkraft, Magnetkraft, Motorkraft, usw.) oder nach ihrer Wirkung (Zugkraft, Druckkraft, Antriebskraft, Verformungskraft, usw.) benannt.
| Kraft | Betrag der Kraft in ![\unit[]{N}](../../_images/math/0cadf526be8f6b6fc1c763f3456a0a9b802a7813.png) |
| Gewichtskraft eines Normalbriefes | 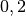 |
| Gewichtskraft einer Tafel Schokolade | 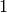 |
| Gewichtskraft von einem Liter Wasser | 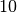 |
| Gewichtskraft von einem Kilogramm Zucker | 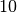 |
| Gewichtskraft eines Menschen | 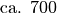 |
| Zugkraft eines PKW | 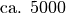 |
| Zugkraft einer Lokomotive | 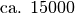 |
| Anziehungskraft der Erde auf den Mond | 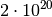 |
Das 3. Newtonsche Gesetz („Kraft und Gegenkraft“)
Zu jeder Kraft gehört eine gleich große Gegenkraft. Kraft und Gegenkraft haben entgegengesetzte Richtungen und wirken auf verschiedene Körper ein – sie können sich somit nicht gegenseitig aufheben.
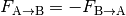
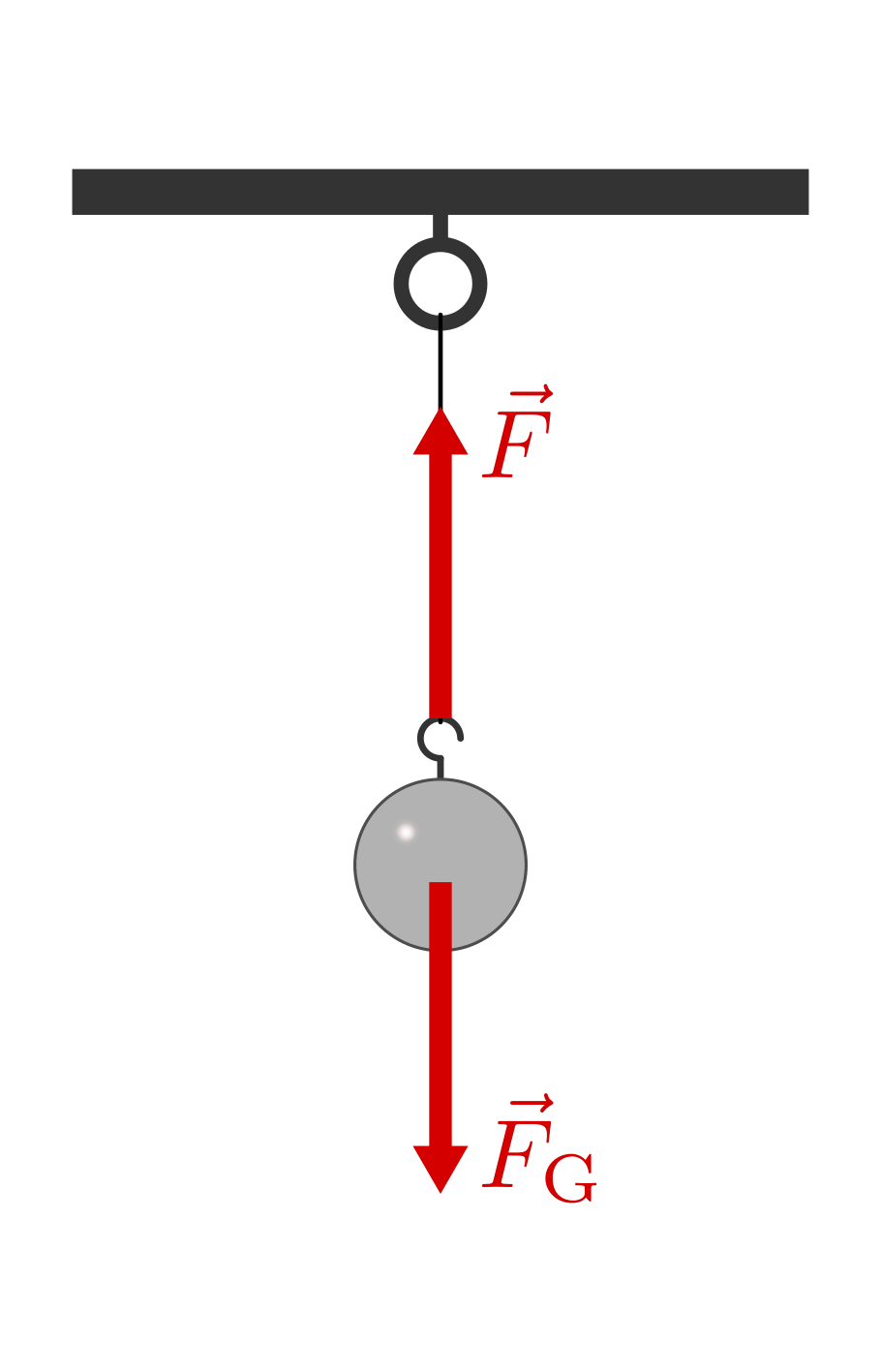
Beispiel:
Ein Gewicht hängt an einem Faden. Der Faden verhindert das Fallen des Probekörpers. In ihm wirkt eine Kraft, die so groß wie das Gewicht des Körpers ist. Beide Kräfte unterscheiden sich aber durch ihre Richtung. Die Kraft im Faden und das Gewicht haben entgegengesetzte Richtungen, sie heben sich in ihrer Wirkung auf.
Schneidet man den Faden durch, so führt der Körper durch die Anziehungskraft der Erde eine geradlinige Bewegung mit konstanter Beschleunigung aus (Luftwiderstand wird vernachlässigt). Da alle Kräfte wechselseitig wirken, zieht der Körper auch die Erde an. Die Erde „fällt“ somit auch auf den Körper zu – die Wirkung ist allerdings so gering, dass wir davon nichts merken.
Betrag, Wirkungslinie und Angriffspunkt¶
Um die Wirkung einer Kraft vorhersagen zu können, muss man nicht nur die Größe (den „Betrag“) einer Kraft kennen, sondern auch wissen, an welchem Punkt sie angreift und in welche Richtung sie wirkt.
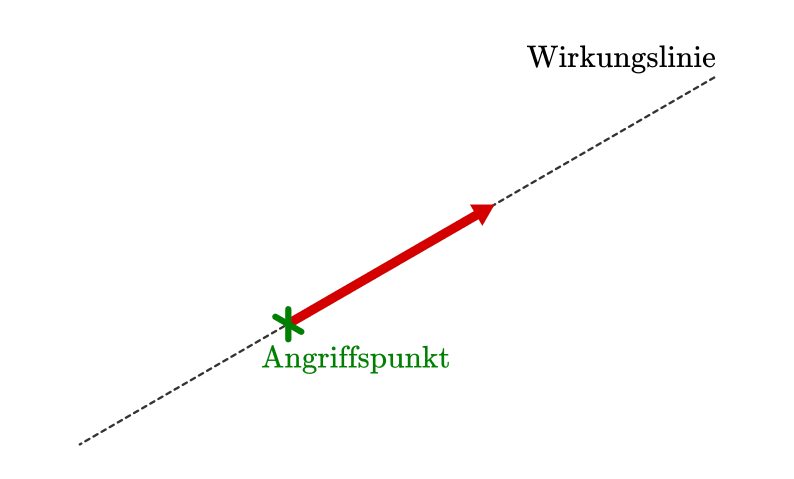
Ein Kraftvektor ist durch seinen Betrag, seine Wirkungslinie und seinen Angriffspunkt eindeutig definiert.
In Koordinatensystemen und Zeichnungen werden Kräfte meist durch Pfeile („Vektoren“) dargestellt. Dabei gilt:
- Die Länge des Pfeils gibt in einem bestimmten Maßstab (beispielsweise
![\unit[1]{N} = \unit[1]{cm}](../../_images/math/94f730f8fab85b36da4d9552b07646f8fd448fa3.png) ) den Betrag der Kraft an. Die Wahl des
Maßstabs ist beliebig, muss aber für alle Kräfte einer Zeichnung gleichermaßen
gelten.
) den Betrag der Kraft an. Die Wahl des
Maßstabs ist beliebig, muss aber für alle Kräfte einer Zeichnung gleichermaßen
gelten. - Der Anfangspunkt des Pfeils ist gleich dem Angriffspunkt der Kraft.
- Die Richtung des Pfeils entspricht der Wirkungslinie der Kraft.
Entlang der Wirkungslinie kann der Kraftvektor bei geeigneter Kraftübertragung beliebig verschoben werden, ohne dass sich an der physikalischen Wirkung der Kraft etwas ändert.
Kraftübertragung mit Seil, Stange und Kette
In vielen Fällen ist es nützlich, eine Kraft „aus der Entfernung“ wirken zu lassen, also ihren Angriffspunkt entlang ihrer Wirkungslinie zu verschieben.
- Mittels Seilen und Ketten lassen sich Zugkräfte auf einen anderen Körper übertragen,
- Mittels Stangen – und bedingt auch mit Drähten – können sowohl Zugkräfte als auch Druckkräfte auf einen anderen Körper übertragen werden.
In Getrieben werden üblicherweise Zahnräder und Zahnstangen zur Kraftübertragung verwendet.
Verformung und Elastizität¶
Kräfte können neben der Geschwindigkeit auch die Form eines Körpers verändern. Je nach Material des Körpers sind Verformungen auf zweierlei Arten möglich:
Elastische Verformung:
Bei einem elastischen Vorgang bildet sich die Verformung eines Körpers zurück, wenn die verformende Kraft nachlässt. Ein typisches elastisches Material ist Gummi, doch auch viele Metalle (beispielsweise Stahl) wirken bei nicht zu großer Krafteinwirkung elastisch.
Beispiel: Ein Gummiball nimmt, wenn keine Kräfte mehr auf ihn einwirken, wieder seine ursprüngliche Form ein.
Plastische Verformung:
Bei einem plastischen Vorgang bleibt die Verformung bestehen, wenn Kraft nicht mehr wirkt. Typische plastische Materialien sind Knetmasse, Wachs, Lehm, Blei, usw.
Beispiel: Die Verformung einer zusammengedrückten Kugel aus Wachs oder Knetmasse bleibt bestehen.
Es gibt keinen Stoff, der vollkommen elastisch oder vollkommen unelastisch ist. Wirken nur geringe Kräfte, so verhält sich beispielsweise Kupfer elastisch. Bei großen Kräften verhält es sich plastisch.
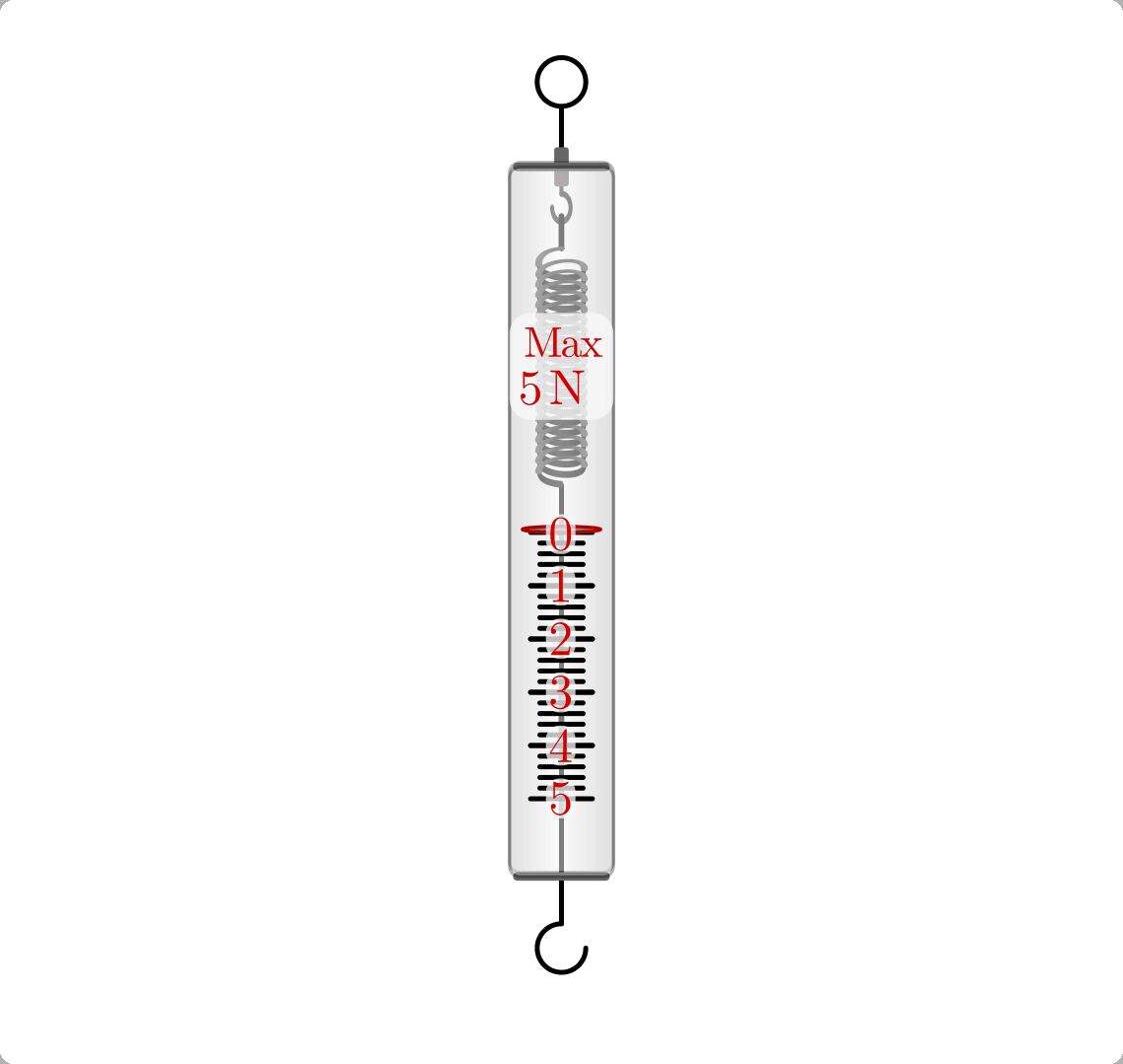
Kraftmessung¶
Zur mechanischen Kraftmessung wird häufig die verformende Wirkung der Kraft genutzt. Je stärker man beispielsweise eine Schraubenfeder verdreht oder sie auseinander zieht, desto größer wird die Spannkraft, mit welcher die Feder sich der Verformung widersetzt. Ist an einer Feder eine geeignete Skala vorhanden, kann die auf sie wirkende Kraft somit direkt abgelesen werden. Da eine Feder nicht beliebig gedehnt werden kann, gibt es Federkraftmesser mit verschiedenen Federhärten und Skalen, die sich für verschiedene Messbereiche eignen.
Bei sich bewegenden Körpern, beispielsweise Autos, kann man die Kraft anhand einer
Geschwindigkeitsänderung des Körper bestimmen – hierzu muss allerdings die
Masse  des Körpers bekannt sein. Misst man die Geschwindigkeitsänderung
des Körpers bekannt sein. Misst man die Geschwindigkeitsänderung
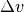 und die dafür benötigte Zeit
und die dafür benötigte Zeit 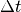 , so kann man die
Beschleunigung
, so kann man die
Beschleunigung 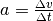 berechnen und erhält durch
Einsetzen in Gleichung (1) die wirkende Kraft
berechnen und erhält durch
Einsetzen in Gleichung (1) die wirkende Kraft  :
:
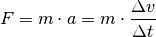
Scheinkräfte¶
Mit Hilfe der Newtonschen Gesetze lässt sich die Bewegung eines Körpers in einem ruhenden oder sich mit konstanter Geschwindigkeit geradlinigen Bezugsystem (einem so genannten „Inertialsystem“) hinreichend beschreiben. In einem beschleunigten Bezugsystem sind zur Beschreibung von Bewegungen jedoch so genannte „Scheinkräfte“ zu berücksichtigen.
Befindet man sich beispielsweise in einem sich gleichmäßig bewegenden oder stehenden Eisenbahnwagen und wirft einen Ball senkrecht in die Luft, so landet dieser auch wieder in der eigenen Hand. Beschleunigt der Zug jedoch, nachdem der Ball die Hand verlassen hatte, so scheint dieser aus der Perspektive des mit dem Zug beschleunigten Werfers im Lauf des Flugs von der Hand weg zu bewegen. Während also für einen außen stehenden Beobachter sich der Zug unter dem sich in horizontaler Richtung gleichförmig bewegenden Ball wegbewegt, muss ein Beobachter im Zug sich eine der Beschleunigung des Zugs entgegengesetzte Kraft auf den Ball hinzu denken, um die Bewegung des Balls richtig vorhersagen können.
Eine nur in einem beschleunigten Bezugsystem auftretende Kraft wird als
Scheinkraft bezeichnet. Sie ist gleich dem Produkt aus der Masse  des
beschleunigten Gegenstands und einer zur Beschleunigung des Bezugsystems
des
beschleunigten Gegenstands und einer zur Beschleunigung des Bezugsystems
 gleich großen, aber in die entgegengesetzte Richtung wirkenden
Beschleunigung
gleich großen, aber in die entgegengesetzte Richtung wirkenden
Beschleunigung 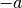 :
:
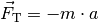
Eine wichtige Scheinkraft ist die Trägheitskraft 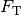 , die
beispielsweise beim Beschleunigen oder Abbremsen von Fahrzeugen auftritt. Ein
Sonderfall dieser Trägheitswirkung ist die Zentrifugalkraft
bei einer kreisförmigen Bewegung. Trägheitskräfte werden auch in technischen
Anwendungen genutzt, wenn durch ein schnelles Abbremsen eines Objekts eine große
Kraft erzielt werden soll, beispielsweise beim Hämmern, Pressen, usw.
, die
beispielsweise beim Beschleunigen oder Abbremsen von Fahrzeugen auftritt. Ein
Sonderfall dieser Trägheitswirkung ist die Zentrifugalkraft
bei einer kreisförmigen Bewegung. Trägheitskräfte werden auch in technischen
Anwendungen genutzt, wenn durch ein schnelles Abbremsen eines Objekts eine große
Kraft erzielt werden soll, beispielsweise beim Hämmern, Pressen, usw.
D’Alembertsches Prinzip
Befindet sich ein Beobachter gemeinsam mit dem beobachteten Objekt in einem
beschleunigten Bezugsystem, so erfährt dieser die gleiche Beschleunigung
 wie das Objekt selbst. Aus Sicht dieses Beobachters befindet sich das
Objekt in Ruhe oder bewegt sich mit konstanter Geschwindigkeit; die auf das
Objekt wirkenden Kräfte addieren sich aus Sicht des mitbeschleunigten
Beobachters somit zu Null.
wie das Objekt selbst. Aus Sicht dieses Beobachters befindet sich das
Objekt in Ruhe oder bewegt sich mit konstanter Geschwindigkeit; die auf das
Objekt wirkenden Kräfte addieren sich aus Sicht des mitbeschleunigten
Beobachters somit zu Null.
Aus Sicht eines ruhenden Beobachters unterscheidet sich die Dynamik des Objekts
(gegenüber der Perspektive eines mitbeschleunigten Beobachters) lediglich um die
Trägheitskraft  . Somit muss in einem ruhenden Bezugsystem
für die am Objekt wirkenden Kräfte gelten:
. Somit muss in einem ruhenden Bezugsystem
für die am Objekt wirkenden Kräfte gelten:
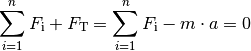
Diese Gleichung ist nach ihrem Entdecker benannt und wird allgemein als D’Alembertsches Prinzip bezeichnet. Es kann genutzt werden, um dynamische Vorgänge auf statische Gleichgewichtsbedingungen zurückführen und somit einfacher berechnen zu können.
Anmerkungen:
| [1] | In mathematischer Schreibweise bedeutet dies, dass der
Geschwindigkeitsvektor
|
| [2] | Streng genommen gilt diese Definition nur dann, wenn die Masse
 des Körpers konstant ist. In allgemeiner Form lässt sich die
Kraft als zeitliche Änderung des Impulses eines
Körpers definieren. des Körpers konstant ist. In allgemeiner Form lässt sich die
Kraft als zeitliche Änderung des Impulses eines
Körpers definieren. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

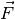 ist proportional zu der Beschleunigung
ist proportional zu der Beschleunigung
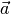 , die ein Körper der Masse
, die ein Körper der Masse 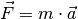
![\unit[1]{N} = \unit[1]{kg} \cdot \unit[1]{\frac{m}{s^2}}](../../_images/math/a963074797aa23bf8204670ac1afc317ebe76897.png)
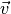 eines Körpers dann konstant bleibt,
wenn die Summe aller
eines Körpers dann konstant bleibt,
wenn die Summe aller  wirkenden Kräfte
wirkenden Kräfte 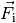 gleich Null ist:
gleich Null ist: