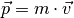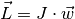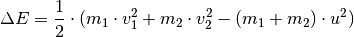Impuls und Drehimpuls¶
Neben der Energie gibt es zwei weitere Größen, die innerhalb eines abgeschlossenen Systems stets konstant bleiben; sie werden als Impuls und Drehimpuls bezeichnet. Die Impulsgesetze werden insbesondere bei mathematischen Beschreibung von Stoßprozessen genutzt, Drehimpulse sind bei Kreisbewegungen und Rotationen von Bedeutung.
Der Impuls¶
Der Bewegungszustand eines Körpers ist neben seiner Geschwindigkeit auch durch seine Masse gekennzeichnet. Der Impuls eines Körpers kennzeichnet die Wucht, die dieser Körper bei einer Translationsbewegung hat.
Definition:
Der Impuls
eines Körpers ist gleich dem Produkt aus seiner Masse
und seiner Geschwindigkeit
:
(1)¶
Einheit:
Die Einheit des Impulses ist gemäß der Definition.
Der Impuls 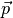 ist eine vektorielle Größe und zeigt in die gleiche
Richtung wie die Geschwindigkeit
ist eine vektorielle Größe und zeigt in die gleiche
Richtung wie die Geschwindigkeit 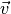 . Der Impuls eines Körpers
ändert sich, wenn sich entweder seine Geschwindigkeit ändert (in Betrag oder
Richtung), oder wenn sich – beispielsweise bei einem Raketenstart – seine
Masse ändert.
. Der Impuls eines Körpers
ändert sich, wenn sich entweder seine Geschwindigkeit ändert (in Betrag oder
Richtung), oder wenn sich – beispielsweise bei einem Raketenstart – seine
Masse ändert.
Mathematisch lässt sich die betragliche Änderung des Impulses somit folgendermaßen ausdrücken:
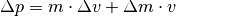
Diese Änderung des Impulses kann in Relation zur Zeit 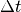 gesetzt
werden, in der die Änderung stattfindet. Damit folgt:
gesetzt
werden, in der die Änderung stattfindet. Damit folgt:
![{\color{white}\ldots \qquad \qquad \quad }\frac{\Delta p}{\Delta t} &=
\frac{m \cdot \Delta v + \Delta m \cdot v}{\Delta t} = \frac{m \cdot \Delta
v}{\Delta t} + \frac{\Delta m \cdot v}{\Delta t} \\[4pt]
&= m \cdot \frac{\Delta v}{\Delta t} + \frac{\Delta m}{\Delta t} \cdot v](../_images/math/973a4da0b9bdb222a835a0511d9bd8c888aaffa8.png)
Der Term 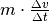 im ersten Teil dieser Summe
kann aufgrund des Zusammenhangs
im ersten Teil dieser Summe
kann aufgrund des Zusammenhangs 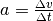 auch als
auch als
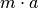 geschrieben werden. Dieser Term entspricht der üblichen
Definition der Kraft
geschrieben werden. Dieser Term entspricht der üblichen
Definition der Kraft 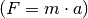 und ist mit der Änderung des
Impulses identisch, sofern die Änderung der Masse gleich Null ist. Andernfalls
muss das 2. Newtonsche Gesetz („Kraftgesetz“) allgemeiner
formuliert werden. Newton selbst hat es in folgender Form angegeben:
und ist mit der Änderung des
Impulses identisch, sofern die Änderung der Masse gleich Null ist. Andernfalls
muss das 2. Newtonsche Gesetz („Kraftgesetz“) allgemeiner
formuliert werden. Newton selbst hat es in folgender Form angegeben:
(2)¶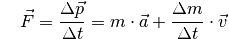
Eine Kraft kann somit als zeitliche Änderung des Impulses aufgefasst werden.
Umgekehrt kann man sich eine Impulsänderung 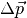 als
„Kraftstoß“ vorstellen, der sich ergibt, wenn eine Kraft
als
„Kraftstoß“ vorstellen, der sich ergibt, wenn eine Kraft 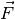 über
einen Zeitraum
über
einen Zeitraum 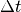 auf einen Körper einwirkt. Es gilt also:
auf einen Körper einwirkt. Es gilt also:
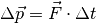
Der Impulserhaltungssatz
Ein System aus mehreren miteinander wechselwirkenden Körpern hat einen Gesamtimpuls, der der Summe aller Einzelimpulse entspricht:
(3)¶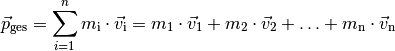
Wenn keine äußeren Kräfte auf das System wirken, dann ist der Gesamtimpuls konstant. Dieser empirisch gefundene Sachverhalt wird Impulserhaltung genannt und stellt neben der Erhaltung der Energie einen der wichtigsten Erhaltungssätze in der Physik dar.
Beispiel 1: Elastischer Stoß zweier Kugeln
Besteht ein System beispielsweise aus zwei Kugeln, die frontal und elastisch
zusammenstoßen, so ist sowohl die Summe der Impulse wie auch die Summe der
Bewegungsenergien vor und nach der Wechselwirkung gleich. Bezeichnet man mit
 eine Geschwindigkeit vor und mit
eine Geschwindigkeit vor und mit 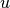 eine Geschwindigkeit
nach dem Stoß, so ergibt sich nach dem Impuls- und Energieerhaltungssatz
folgendes Gleichungssystem:
eine Geschwindigkeit
nach dem Stoß, so ergibt sich nach dem Impuls- und Energieerhaltungssatz
folgendes Gleichungssystem:
![m_1 \cdot v_1 + m_2 \cdot v_2 &= m_1 \cdot u_1 + m_2 \cdot u_2
\\[4pt] \frac{1}{2} \cdot m_1 \cdot v_1^2 \, + \, \frac{1}{2}\cdot m_2 \cdot v_2^2 &=
\frac{1}{2} \cdot m_1 \cdot u_1^2 \, + \, \frac{1}{2} \cdot m_2 \cdot u_2^2](../_images/math/10a2f29e4fc30ef2e52ff5278c084c561d0efac0.png)
Da in der zweiten Gleichung alle Terme den Faktor 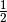 enthalten,
kann dieser ausgeklammert und gekürzt werden. Durch Umstellen der Terme können
beide Gleichungen auf folgende Form gebracht werden:
enthalten,
kann dieser ausgeklammert und gekürzt werden. Durch Umstellen der Terme können
beide Gleichungen auf folgende Form gebracht werden:
![m_1 \cdot (v_1 - u_1) &= m_2 \cdot (v_2 - u_2) \\[4pt]
m_1 \cdot (v_1^2 - u_1^2) &= m_2 \cdot (v_2^2 - u_2^2)](../_images/math/399b1e4beed48799a141211af9af5b1e4dcb1ec3.png)
Da 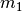 und
und 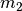 ungleich Null sind und – als Bedingung für einen
Stoß – zusätzlich
ungleich Null sind und – als Bedingung für einen
Stoß – zusätzlich 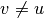 ist, kann zur Lösung des Gleichungssystems
die zweite Gleichung (nach Anwendung der binomischen Formel) durch die erste
geteilt werden.[1] Das Ergebnis lautet:
ist, kann zur Lösung des Gleichungssystems
die zweite Gleichung (nach Anwendung der binomischen Formel) durch die erste
geteilt werden.[1] Das Ergebnis lautet:
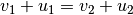
Diese Gleichung wurde durch Anwendung äquivalenter Umformungen aus der ursprünglichen Energieerhaltungs-Gleichung gebildet. Gemeinsam mit der ursprünglichen Impulserhaltungs-Gleichung stellt sie ein nun ein lineares Gleichungssystem dar:
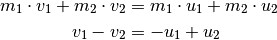
Die beiden gesuchten Größen 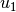 und
und 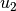 stehen dabei jeweils
auf der rechten Seite. Löst man die beispielsweise die zweite Gleichung nach
stehen dabei jeweils
auf der rechten Seite. Löst man die beispielsweise die zweite Gleichung nach
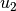 auf und setzt das Ergebnis
auf und setzt das Ergebnis 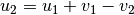 in die
erste Gleichung ein, so erhält man:
in die
erste Gleichung ein, so erhält man:
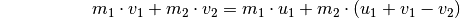
Dies ergibt, wenn man die rechte Seite ausmultipliziert und die Gleichung nach
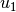 auflöst:
auflöst:
(4)¶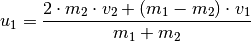
Entsprechend ergibt sich für die Geschwindigkeit 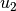 :
:
(5)¶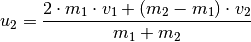
Diese beiden Ergebnisse gelten für beliebige Kugelmassen und Anfangsgeschwindigkeiten. Betrachtet man einige Sonderfälle, so erhält man folgende vereinfachte Ergebnisse:
Sind beide Kugeln gleich schwer (
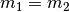 ) und ist die zweite anfangs
in Ruhe
) und ist die zweite anfangs
in Ruhe 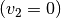 , so überträgt die erste Kugel beim Stoß ihren
gesamten Impuls auf die zweite Kugel. Es gilt nämlich in diesem Fall:
, so überträgt die erste Kugel beim Stoß ihren
gesamten Impuls auf die zweite Kugel. Es gilt nämlich in diesem Fall:![u_1 &= \frac{2 \cdot m_1 \cdot 0 \; + 0 \cdot v_1}{2 \cdot m_1} = 0 \\[4pt]
u_2 &= \frac{2 \cdot m_1 \cdot v_1 + 0 \cdot v_2}{2 \cdot m_1} = v_1](../_images/math/642cb635e664eab14c90512e4ae3cc72f7af6614.png)
Ist die erste Kugel sehr viel leichter als die zweite Kugel und ruht diese (
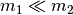 und
und 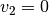 ), so prallt die erste Kugel mit einer
(nahezu) gleich großen, jedoch entgegengesetzt gerichteten Geschwindigkeit
zurück. Es gilt in diesem Fall näherungsweise:
), so prallt die erste Kugel mit einer
(nahezu) gleich großen, jedoch entgegengesetzt gerichteten Geschwindigkeit
zurück. Es gilt in diesem Fall näherungsweise:
![{\color{white}\ldots \qquad \quad }u_1 &\approx \frac{2 \cdot m_2 \cdot 0
- m_2 \cdot v_1}{m_2} = -v_1 \\[4pt]
u_2 &\approx \phantom{\ldots}\;\; \frac{ \phantom{\ldots}0 \cdot v_2
\phantom{\ldots}}{m_2} \phantom{\ldots}\;\, = 0](../_images/math/cd39ab8214fc11026c671d6b289f0948d908f51c.png)
- Ist die erste Kugel sehr viel schwerer als die zweite Kugel und ruht diese
(
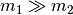 und
und 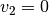 ), so bewegt sich die erste Kugel mit
nahezu gleicher Geschwindigkeit weiter; die zweite Kugel wird auf die doppelte
Geschwindigkeit der ersten Kugel beschleunigt. Es gilt in diesem Fall
näherungsweise:
), so bewegt sich die erste Kugel mit
nahezu gleicher Geschwindigkeit weiter; die zweite Kugel wird auf die doppelte
Geschwindigkeit der ersten Kugel beschleunigt. Es gilt in diesem Fall
näherungsweise:
![{\color{white}\ldots \qquad \quad }u_1 &\approx \frac{2 \cdot m_2 \cdot 0
+ m_1 \cdot v_1}{m_1} = +v_1 \\[4pt]
u_2 &\approx \frac{ 2 \cdot m_1 \cdot v_1 - m_1 \cdot 0}{m_1} \approx 2
\cdot v_1](../_images/math/4ad17791c8f0f640a4df3cd090dff0d64f8bfd30.png)
Stoßen die Kugeln nicht frontal, sondern schräg aufeinander, so muss das obige Rechenschema komponentenweise für die drei Raumrichtungen komponentenweise angewendet werden.
Beispiel 2: Unelastischer Stoß zweier Kugeln
Stoßen zwei Kugeln unelastisch aufeinander, so bewegen sich beide nach dem Stoß
mit der gleichen Geschwindigkeit 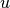 entlang einer gemeinsamen Richtung
hin fort. Die Richtung und der Betrag der Geschwindigkeit
entlang einer gemeinsamen Richtung
hin fort. Die Richtung und der Betrag der Geschwindigkeit 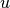 kann anhand
des Impulserhaltungs-Gleichung direkt berechnet werden:
kann anhand
des Impulserhaltungs-Gleichung direkt berechnet werden:
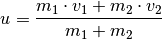
Der Energie-Erhaltungssatz gilt hingegen in diesem Fall nicht – durch die unelastische Verformung wird mechanische Energie in Wärme umgewandelt.[2]
Teilelastische Stoßprozesse
In vielen Fällen handelt es sich bei Stößen weder einem komplett elastischen noch um einen komplett unelastischen Vorgang, sondern vielmehr um einen teilelastischen Prozess: Es wird dabei nur ein Teil der Verformungsarbeit wieder zurück in kinetische Energie gewandelt. Die Geschwindigkeiten der beteiligten Gegenstände sind nach einem teilelastischen Stoß folglich kleiner als bei einem elastischen Stoß.
Für die Bewegungsenergien 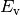 und
und 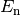 vor und
nach dem Stoß gilt:
vor und
nach dem Stoß gilt:
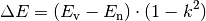
Die Zahl 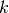 wird hierbei als Stoßzahl bezeichnet; sie kann mittels
folgender Formel experimentell bestimmt werden:
wird hierbei als Stoßzahl bezeichnet; sie kann mittels
folgender Formel experimentell bestimmt werden:
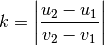
Die Stoßzahl 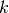 ist gleich Null für komplett unelastische Prozesse und
gleich Eins für komplett elastische Prozesse. Für teilelastische Prozesse
ergibt sich eine Zahl zwischen Null und Eins, die den Elastizitätsgrad des
Prozesses angibt.
ist gleich Null für komplett unelastische Prozesse und
gleich Eins für komplett elastische Prozesse. Für teilelastische Prozesse
ergibt sich eine Zahl zwischen Null und Eins, die den Elastizitätsgrad des
Prozesses angibt.
Der Drehimpuls¶
In ähnlicher Weise, wie sich bei der Definition des Impulses der Beschreibung von Translationsbewegungen als hilfreich herausgestellt hat, so hat sich auch bei der Beschreibung von Rotationsbewegungen die Einführung eines so genannten Drehimpulses als nützlich erwiesen.
Der Drehimpuls eines Körpers ist von seinem Trägheitsmoment und von seiner Winkelgeschwindigkeit abhängig und kennzeichnet die Wucht, die dieser Körper bei einer Rotationsbewegung aufweist.
Definition:
Der Drehimpuls
eines Körpers ist gleich dem Produkt aus seinem Trägheitsmoment
und seiner Winkelgeschwindigkeit
:
(6)¶
Der Drehimpuls ist eine vektorielle Größe und zeigt in die gleiche Richtung wie die Winkelgeschwindigkeit, also senkrecht zur Drehebene. Der Betrag des Drehimpuls eines rotierenden Körpers ändert sich, wenn sich entweder der Betrag seiner Winkelgeschwindigkeit oder seine Massenverteilung und somit sein Trägheitsmoment ändert.
Mathematisch lässt sich die betragliche Änderung des Drehimpulses folgendermaßen ausdrücken:

Diese Änderung des Impulses kann in Relation zur Zeit 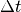 gesetzt
werden, in der die Änderung stattfindet. Damit folgt:
gesetzt
werden, in der die Änderung stattfindet. Damit folgt:
![{\color{white}\ldots \qquad \qquad \quad }\frac{\Delta L}{\Delta t} &=
\frac{J \cdot \Delta \omega + \Delta J \cdot \omega}{\Delta t} = \frac{J
\cdot \Delta \omega}{\Delta t} + \frac{\Delta J \cdot \omega}{\Delta t}
\\[4pt]
&= J \cdot \frac{\Delta \omega}{\Delta t} + \frac{\Delta J}{\Delta t} \cdot
\omega](../_images/math/fd9e7aa695779404d52512003f978e59dbd7ad17.png)
Der Term 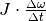 im ersten Teil dieser
Summe lässt sich aufgrund des Zusammenhangs
im ersten Teil dieser
Summe lässt sich aufgrund des Zusammenhangs 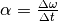 auch als
auch als  schreiben. Dieser
Term kann als Drehmoment aufgefasst werden
schreiben. Dieser
Term kann als Drehmoment aufgefasst werden 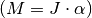 und ist mit der Änderung des Drehimpulses identisch, sofern die
Änderung des Trägheitsmoments gleich Null ist. Andernfalls muss diese zusätzlich
berücksichtigt werden:[3]
und ist mit der Änderung des Drehimpulses identisch, sofern die
Änderung des Trägheitsmoments gleich Null ist. Andernfalls muss diese zusätzlich
berücksichtigt werden:[3]
(7)¶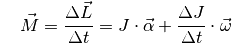
Eine Drehmoment kann somit allgemein als zeitliche Änderung des Drehimpulses aufgefasst werden.
Der Drehimpulserhaltungssatz
Ein System aus mehreren miteinander wechselwirkenden Körpern hat einen Gesamt-Drehimpuls, welcher der Summe aller einzelnen Drehimpulse entspricht:
(8)¶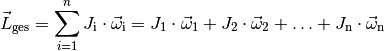
Wenn keine äußeren Drehmomente auf das System wirken, dann ist der Gesamt-Drehimpuls konstant. Dieser empirisch gefundene Sachverhalt wird Drehimpulserhaltung genannt und stellt gemeinsam mit der Impulserhaltung und der Erhaltung der Energie einen der wichtigsten Erhaltungssätze der Mechanik dar.
Anmerkungen:
| [1] | Nach der binomischen Formel ist 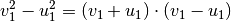 . Der letzte Term kann dabei gekürzt werden. . Der letzte Term kann dabei gekürzt werden. |
| [2] | Wie groß der Verlust an mechanischer Energie ist, kann aus der Differenz der Bewegungsenergien beider Kugeln vor und nach dem Stoß berechnet werden:
Experimentell lässt sich ein unelastischer Stoß beispielsweise dadurch erreichen, dass an dem Berührungspunkt der Kugeln ein kleines Stück Kaugummi aufgeklebt wird. |
| [3] | Beispielsweise verringern Eiskunstläufer(innen) bei Pirouetten durch ein Einziehen der zunächst ausgestreckten Arme bewusst ihr Trägheitsmoment, um damit – ohne zusätzliche Energiezufuhr – eine deutlich höhere Winkelgeschwindigkeit zu erreichen. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.