Mechanische Energie

Zum Heben oder Beschleunigen eines beliebigen Körpers oder zum Verformen eines elastischen Körpers – beispielsweise zum Spannen einer Feder – muss stets mechanische Arbeit verrichtet werden. Der Körper wird dadurch in einen neuen Zustand versetzt und ist dabei in der Lage seinerseits Arbeit verrichten zu können. Dieser Zustand wird durch die physikalische Größe „Energie“ beschrieben.

Definition:

Unter Energie versteht man die Fähigkeit eines Körpers, Arbeit zu verrichten. Energie ist damit mit „gespeicherter Arbeit“ identisch.

Einheit:

Die Energie wird in der gleichen Einheit wie die Arbeit, also in Joule (\unit{J}) angegeben.

\unit[1]{J} = \unit[1]{N} \cdot \unit[1]{m} = \unit[1]{W \cdot s}

Zur Beschreibung großer Energiemengen werden häufig die Einheiten Kilojoule (\unit[1]{kJ} = \unit[1\,000]{J}) und Megajoule (\unit[1]{MJ} = \unit[1\,000\,000]{J}) genutzt. Darüber hinaus werden Energiemengen anhand des Zusammenhangs „Energie ist Leistung mal Zeit“ oftmals auch in (Kilo-)Wattstunden angegeben.

\unit[1]{Wh} = \unit[1]{W} \cdot \unit[3\,600]{s} &= \unit[3\,600]{W \cdot s} = \unit[3\,600]{J} \\[4pt] \unit[1]{kWh} &= \unit[1\,000]{Wh}

Arten mechanischer Energie

Bei mechanischen Prozessen treten folgende Arten mechanischer Energie auf:[1]

Die potentielle Energie („Höhenenergie“)

Um einen Körper entgegen der Schwerkraft anzuheben, muss Hubarbeit verrichtet werden. Diese ist dann in Form von „Höhenenergie“ im Körper gespeichert. Die Höhenenergie wird häufig auch als potentielle Energie bezeichnet, da sie durch den freien Fall des angehobenen Körpers wiedergewonnen werden kann.

Definition:

Die potentielle Energie E_{\mathrm{pot}} ist gleich dem Produkt aus der Gewichtskraft F_{\mathrm{G}} = m \cdot g eines Körpers mit Masse m sowie der Höhe h, die dieser angehoben wird:

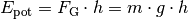
(1)E_{\mathrm{pot}} = F_{\mathrm{G}} \cdot h = m \cdot g \cdot h

Hierbei steht 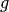g für den Ortsfaktor. Auf der Erdoberfläche gilt g \approx \unit[9,81]{\frac{N}{kg}}.

Die potentielle Energie eines Körpers als Resultat einer verrichteten Hubarbeit lässt sich schwerlich als Absolutwert angeben. Steht beispielsweise ein Gegenstand auf einem Tisch, so hat er gegenüber dem Boden meist eine andere Höhenenergie als gegenüber der Meereshöhe. Bei Rechnungen legt man daher ein Null-Niveau fest, auf das man dann die einzelnen potentiellen Energien bezieht.[2]

Die Spannenergie

Beim Verformen eines elastischen Körpers wird die verrichtete Spannarbeit als Spannenergie im Körper gespeichert und bei einer Rückverformung wieder freigesetzt. Bekannte Beispiele hierfür sind das Spannnen einer Schraubenfeder, das Zusammendrücken einer Druckfeder, das Hüpfenlassen eines Flummis, usw.

Definition:

Die Spannenergie E_{\mathrm{Spann}} eines verformten Körpers mit der Federkonstanten D ist gleich dem Produkt aus der während der Verformung durchschnittlich wirkenden Spannkraft \bar{F} _{\mathrm{S}} = \frac{1}{2} \cdot F_{\mathrm{S}} = \frac{1}{2} \cdot D \cdot s und der Ausdehnung s aus der Ruhelage:

(2)E_{\mathrm{Spann}} = \bar{F} _{\mathrm{S}} \cdot s = \frac{1}{2} \cdot D \cdot s^2

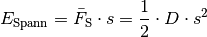
Die gespeicherte Spannenergie nimmt somit, solange es sich sich um einen elastischen Prozess handelt, quadratisch mit der Verformung des Körpers zu.

Die kinetische Energie („Bewegungsenergie“)

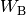Um einen Körper zu beschleunigen, also ihn auf eine bestimmte Geschwindigkeit v zu bringen, muss die Beschleunigungsarbeit W_{\mathrm{B}} verrichtet werden. Diese ist dann in Form von Bewegungsenergie (häufig auch „kinetische Energie“ genannt) im Körper gespeichert.

Definition:

Die kinetische Energie E_{\mathrm{Kin}} ist gleich dem Produkt aus der Masse m eines Körpers und dem Quadrat seiner Geschwindigkeit v:

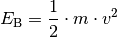
(3)E_{\mathrm{B}} = \frac{1}{2} \cdot m \cdot v^2

Die Bewegungsenergie eines Körpers nimmt somit quadratisch mit seiner Geschwindigkeit zu.

Die Rotationsenergie

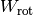Um einen Körper auf eine bestimmte Winkelgeschwindigkeit \omega zu bringen, muss die Rotationsarbeit W_{\mathrm{rot}} verrichtet werden. Diese ist dann in Form von Rotationsenergie im Körper gespeichert.

Definition:

Die Rotationsenergie E_{\mathrm{rot}} ist gleich dem Produkt aus dem Trägheitsmoment J eines Körpers und dem Quadrat seiner Winkelgeschwindigkeit \omega:

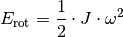
(4)E_{\mathrm{rot}} = \frac{1}{2} \cdot J \cdot \omega^2

Die kinetische Gesamtenergie eines rollenden Körpers ist gleich der Summe seiner Bewegungsenergie und seiner Rotationsenergie:

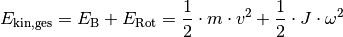
E_{\mathrm{kin,ges}} = E_{\mathrm{B}} + E_{\mathrm{Rot}} = \frac{1}{2} \cdot m \cdot v^2 + \frac{1}{2} \cdot J \cdot \omega^2

Der Energie-Erhaltungssatz

Bei rein mechanischen Vorgängen bleibt die Summe der mechanischen Energien (Höhenenergie, Bewegungsenergie und Spannenergie) konstant.

„Energie kann weder erzeugt noch vernichtet,
sondern stets nur von einer Form in andere
umgewandelt werden.“

Beispiel:

  • Bei einem schwingenden Pendel findet auf dem Weg von der maximalen Auslenkung zur Ruhelage eine kontinuierliche Umwandlung von Höhenenergie in Bewegungsenergie und umgekehrt statt; umgekehrt findet eine kontinuierliche Umwandlung von Bewegungsenergie in Höhenenergie statt, wenn sich der Pendelkörper vom Durchgang durch die Ruhelage in Richtung der maximalen Auslenkung bewegt. Ohne Luftwiderstand und Reibung setzen sich diese Energie-Umwandlungen beliebig oft fort.

In der Praxis treten allerdings in der Regel nicht zu vernachlässigende Reibungseffekte auf, die mechanische Energie in Wärme umwandeln; diese Energieform zählt allerdings nicht zu den mechanischen Energieformen.[3]

Anmerkungen:

[1]Weitere Energieformen sind elektrische Energie, magnetische Energie, thermische Energie (Wärme), Strahlungsenergie (beispielsweise Licht), Kernenergie und chemische Energie.
[2]Arbeit kann in diesem Sinn als Energiemenge aufgefasst werden, die zum Anheben eines Gegenstands auf ein anderes Energie-Niveau nötig ist.
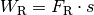[3]Diese für den weiteren mechanischen Prozess „verloren gegangene“ Energie ist dann gleich der verrichteten Reibungsarbeit W_{\mathrm{R}} = F_{\mathrm{R}} \cdot s.

Hinweis

Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.