Elektrische Arbeit, Energie und Leistung

Elektrische Arbeit und Energie

Zur Bereitstellung einer bestimmten Menge an elektrischer Energie muss durch einen Stromgenerator ein entsprechender Betrag an Arbeit aufgewendet werden.[1]

Zur Herleitung einer Formel für die elektrische Arbeit 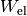W_{\mathrm{el}} kann man die Definitionen der elektrischen Spannung U und der elektrischen Stromstärke I miteinander kombinieren. Aus der Definition der elektrischen Spannung folgt:

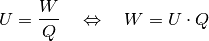
(1)U = \frac{W}{Q} \quad \Leftrightarrow \quad W = U \cdot Q

Die Ladung 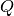Q kann wiederum mit Hilfe der Definition der Stromstärke folgendermaßen beschrieben werden:

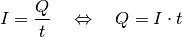
(2)I = \frac{Q}{t} \quad \Leftrightarrow \quad Q = I \cdot t

Insgesamt ergibt die Kombination dieser beiden Gleichungen folgende Formel für die elektrische Arbeit:

Definition:

Die elektrische Arbeit, die ein Stromgenerator verrichtet, ist proportional zur Spannung U und zur Stromstärke I des bereitgestellten Stroms sowie zur Zeitdauer t, über die sich der Stromfluss erstreckt.

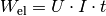
(3)W_{\mathrm{el}} = U \cdot I \cdot t

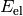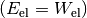Die aufgebrachte elektrische Arbeit kann entweder direkt genutzt oder als elektrische Energie E_{\mathrm{el}} in Kondensatoren und Akkumulatoren gespeichert werden (E_{\mathrm{el}} = W_{\mathrm{el}}).[2]

Einheit:

Die elektrische Arbeit sowie die elektrische Energie wird in Joule (\unit[1]{J} = \unit[1]{W \cdot s}) oder gebräuchlicher in Wattstunden (\unit{Wh}) bzw. Kilowattstunden (\unit{kWh}) angegeben. Dabei gelten folgende Zusammenhänge:

\unit[1]{J} &= \unit[1]{W \cdot s} = \unit[1]{V} \cdot \unit[1]{A} \cdot \unit[1]{s} \\ \unit[1]{Wh} &= \unit[60 \cdot 60]{W \cdot s} = \unit[3\,600]{Ws}

\unit[1]{kWh} &= \unit[1\,000]{Wh}

Elektrische Leistung

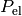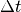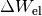Die elektrische Leistung P_{\mathrm{el}}, die ein Stromgenerator aufbringt oder ein Verbraucher benötigt, ist gleich der je Zeit \Delta t verrichteten elektrischen Arbeit \Delta W_{\mathrm{el}}:

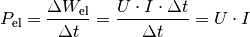
P_{\mathrm{el}} = \frac{\Delta W_{\mathrm{el}}}{\Delta t} = \frac{U \cdot I \cdot \Delta t}{\Delta t} = U \cdot I

Damit lässt sich die elektrische Leistung folgendermaßen definieren:

Definition:

Die elektrische Leistung P_{\mathrm{el}}, die von einem elektronischen Bauteil oder Stromkreis umgesetzt wird, ist proportional zu der am Bauteil anliegenden Spannung U sowie der durch das Bauteil fließenden Stromstärke I.

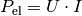
(4)P _{\mathrm{el}} = U \cdot I

Einheit:

Ebenso wie die mechanische Leistung wird die elektrische Leistung in der Einheit Watt (\unit{W}) angegeben. Dabei gilt:[3]

\unit[1]{W} = \unit[1]{V} \cdot \unit[1]{A}

Auf fast allen Elektro-Geräten findet sich neben der Angabe der zulässigen Betriebsspannung auch eine Angabe einer damit verbundenen elektrischen Stromstärke oder Leistung.[4] Zu beachten ist dabei, dass diese Werte nur bei der angegebenen Spannung gelten; da eine höhere Spannung in der Regel auch eine höhere Stromstärke zur Folge hat, nimmt die Leistung mit zunehmender Spannung überproportional zu.

Exkurs: Wärmeentwicklung in elektrischen Bauteilen

Mittels des Ohmschen Gesetzes 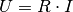U = R \cdot I kann der obige Zusammenhang 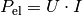P_{\mathrm{el}} = U \cdot I zwischen der elektrischen Leistung 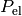P_{\mathrm{el}} sowie der Spannung U und der Stromstärke I auch folgendermaßen ausgedrückt werden:

  • Setzt man für die Stromstärke 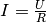I = \frac{U}{R} in die Leistungs-Gleichung (4) ein, so erhält man:

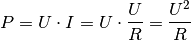
    (5)P = U \cdot I = U \cdot \frac{U}{R} = \frac{U^2}{R}

  • Setzt man für die Spannung 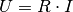U = R \cdot I in die Leistungs-Gleichung (4) ein, so erhält man:

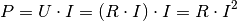
    (6)P = U \cdot I = (R \cdot I) \cdot I = R \cdot I^2

Bei beiden Darstellungen erkennt man, dass die elektrische (Heiz-)Leistung bei konstant bleibendem Widerstand quadratisch mit einer zunehmenden Spannung beziehungsweise Stromstärke ansteigt.

Beispiel:

  • Auf einem regelbaren Demo-Widerstand ist ein maximaler Widerstandswert von R_{\mathrm{max}} = \unit[50]{\Omega} angegeben und eine maximale Belastbarkeit von P_{\mathrm{max}} = \unit[0,5]{W}.

    • Wie groß darf die am Widerstand anliegende Spannung 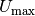U_{\mathrm{max}} eines regelbaren Netzgerätes maximal sein, wenn kein zusätzliches Bauteil im Stromkreis eingebaut ist?
    • Auf welchen Wert U muss die Spannung gesenkt werden, wenn der Widerstand auf R = \unit[25]{\Omega} eingestellt ist?

    Die jeweils maximal mögliche Spannung kann bei einem gegebenen Widerstand und einer gegebenen maximalen Leistung berechnet werden, indem man die Formel (5) nach U auflöst. Man erhält für P_{\mathrm{max}} = \unit[0,5]{W} und R=\unit[50]{\Omega}:

    P_{\mathrm{max}} = \frac{U_{\mathrm{max}}^2 }{R_{\mathrm{max}}} \quad \Longleftrightarrow \quad U_{\mathrm{max}} = \sqrt{P_{\mathrm{max}} \cdot R_{\mathrm{max}}} \\ U_{\mathrm{max}} = \sqrt{\unit[0,5]{W} \cdot \unit[50]{\Omega}} = \unit[5,0]{V}

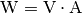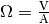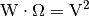    Die Einheit ergibt sich aus \unit{W} = \unit{V \cdot A} und \unit{\Omega} = \unit{\frac{V}{A}}; als Produkt ergibt also die Einheit \unit{W \cdot \Omega} = \unit{V^2}.

    Reduziert man den Widerstand auf R=\unit[25]{\Omega}, so darf bei einer gleichen maximalen Belastbarkeit nur folgende Spannung U angelegt werden:

    U = \sqrt{P_{\mathrm{max}} \cdot R} = \sqrt{\unit[0,5]{W} \cdot \unit[25]{\Omega}} \approx \unit[3,54]{V}

    Bei einem geringeren Widerstandswert muss also auch die Spannung geringer gewählt werden, um das Bauteil nicht zu überlasten.

Stromerzeugung und Stromverbrauch

In jedem Stromkreis muss die Menge der bereitgestellten Energie – da die Gesamtenergie stets erhalten bleibt und elektrische Ladung weder erzeugt noch vernichtet, sondern nur übertragen werden kann – stets der Menge an verbrauchter elektrischer Energie entsprechen.[5]

In einem so großen Stromnetz wie dem der Bundesrepublik Deutschland gibt es selbstverständlich mehr als einen Stromgenerator; insgesamt gesehen muss der Kraftwerkspark allerdings die Verbraucherlast tragen sowie die sich beim Stromtransport ergebenden Leitungsverluste ausgleichen. Bei einer möglichst optimalen Zusammenstellung der Gesamtleistung mittels der verschiedenen Kraftwerkstypen sind ökologische, ökonomische sowie technische Aspekte gleichermaßen von Bedeutung.

Anmerkungen:

[1]

Spannung erzeugende Geräte, die zur Energie-Gewinnung Treibstoffe verbrennen, haben meist einen Verbrennungsmotor oder eine Gas-Turbine als Antrieb; der eigentliche Generator wandelt dann die mechanische Energie in elektrische Energie um.

Im verallgemeinerten Sinn bezeichnet man sämtliche Spannung erzeugende Geräte als Generatoren, also beispielsweise auch Solarzellen oder Thermo-Elemente.
[2]Streng genommen speichern Akkumulatoren die zugeführte elektrische Energie in Form von chemischer Energie. Beide Energieformen lassen sich allerdings (bis auf geringe Wärmeverluste) vollständig ineinander umwandeln – ein voll geladener Akkumulator stellt bei seiner Nutzung wiederum elektrische Energie bereit.
[3]Für größere Leistungsangaben ist auch die Einheit Kilowatt (\unit[]{kW}) gebräuchlich. Dabei gilt: \unit[1]{kW} = \unit[1\,000]{W}
[4]Die jeweils fehlende Angabe kann durch die beiden bekannten Größen mittels Gleichung (4) bestimmt werden.
[5]Auch in Speicheranlagen wie Pumpspeicherkraftwerken oder Akkumulatoren wird zunächst elektrische Energie verbraucht, z.B. um eine große Menge Wasser auf eine bestimmte Höhe zu pumpen oder bestimmte chemische Reaktionen zu ermöglichen; umgekehrt können derartige Anlagen bei Bedarf die gespeicherte Energiemenge mit nur geringen (Wärme-)Verlusten wieder als elektrische Energie bereitstellen.

Download:

Hier kann die Handreichung zum Vortrag Ökologisch sinnvolle Stromerzeugung (2011, PDF, 10 Seiten) heruntergeladen werden.

Hinweis

Zu diesem Abschnitt gibt es Übungsaufgaben.