Leiter, Halbleiter und Isolatoren¶
Ob ein elektrischer Strom in einem Stoff fließen kann, hängt von der Anzahl der frei beweglichen Ladungsträger innerhalb des Stoffes ab.
Leiter¶
Elektrische Leiter werden Stoffe genannt, in denen sich Ladungen leicht bewegen können. Die bekanntesten Leiter sind Metalle, Graphit, Säuren, Laugen und Salzlösungen.
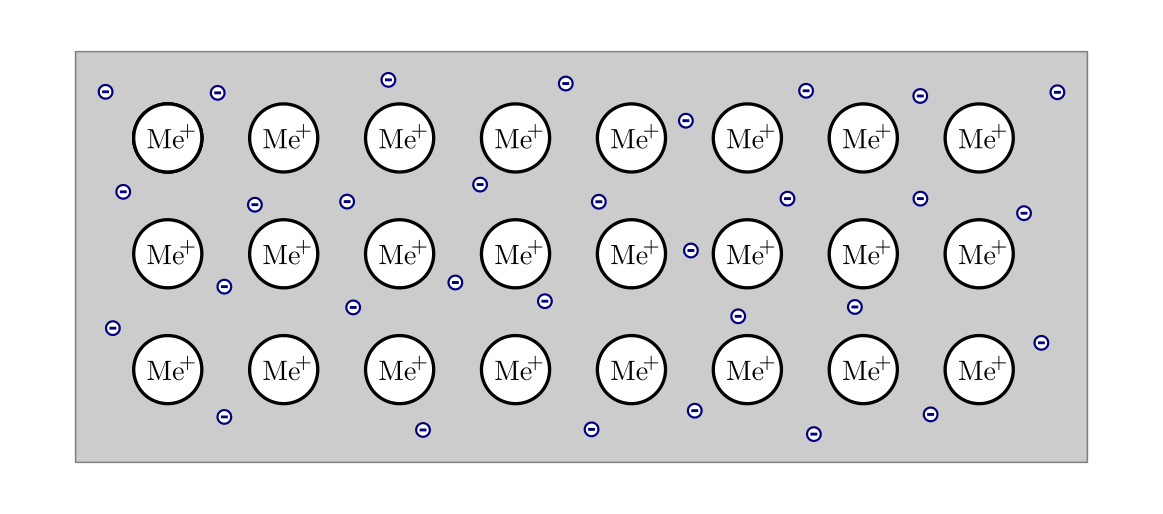
In Metallen sind die einzelnen Atome in einer Gitterstruktur angeordnet, wobei
sich die äußersten Elektronen („Valenzelektronen“) frei entlang des gesamten
Gitters bewegen können („Metallbindung“, „Elektronengas“). Bei nur einem
ungebundenem Elektron je Atom steht dabei eine enorme Zahl an Ladungsträgern –
etwa 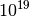 Elektronen je Kubik-Millimeter! – für den Ladungstransport
frei zur Verfügung.[1]
Elektronen je Kubik-Millimeter! – für den Ladungstransport
frei zur Verfügung.[1]
Bei höheren Temperaturen führen die Atomrümpfe eines Metallgitters immer stärkere Wärme-Schwingungen um ihre Ruhelagen aus. Die freien Elektronen werden dadurch in ihrer Beweglichkeit eingeschränkt, was zu einem höheren elektrischen Widerstand führt. Da die Zunahme des Widerstands in guter Näherung linear zur Erwärmung ist, kann der Widerstandswert eines Leiters mit folgender Formel berechnet werden:
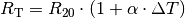
Hierbei gibt 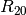 den Widerstandswert bei Raumtemperatur
den Widerstandswert bei Raumtemperatur
![(\unit[20]{\degree C})](../_images/math/0ed10376129ece5149dcb08388a38a0eaeedfb8c.png) an,
an,  entspricht der
Temperaturdifferenz zu diesem Referenzwert (ebenfalls in
entspricht der
Temperaturdifferenz zu diesem Referenzwert (ebenfalls in 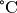 ). Der so genannte „Temperaturbeiwert“
). Der so genannte „Temperaturbeiwert“  ist materialabhängig
und wird in
ist materialabhängig
und wird in 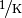 angegeben.
angegeben.
| Material | Temperaturbeiwert  in in 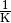 |
| Aluminium | 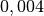 |
| Blei | 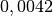 |
| Eisen | 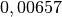 |
| Konstantan | 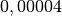 |
| Kupfer | 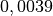 |
| Silber | 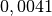 |
| Zink | 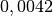 |
Bei niedrigen Temperaturen nehmen die Wärme-Schwingungen der Atomrümpfe und der elektrische Widerstand entsprechend ab; in vielen Metallen verschwindet der elektrische Widerstand ab einer materialspezifischen Temperatur sogar vollständig („Supraleitung“).
In Flüssigkeiten können durch Lösungsvorgänge elektrisch geladene Atome und Moleküle („Ionen“) auftreten. Diese sind zwar bedeutend schwerer als Elektronen, können aber dennoch als freie Ladungsträger den elektrischen Strom leiten.
Halbleiter¶
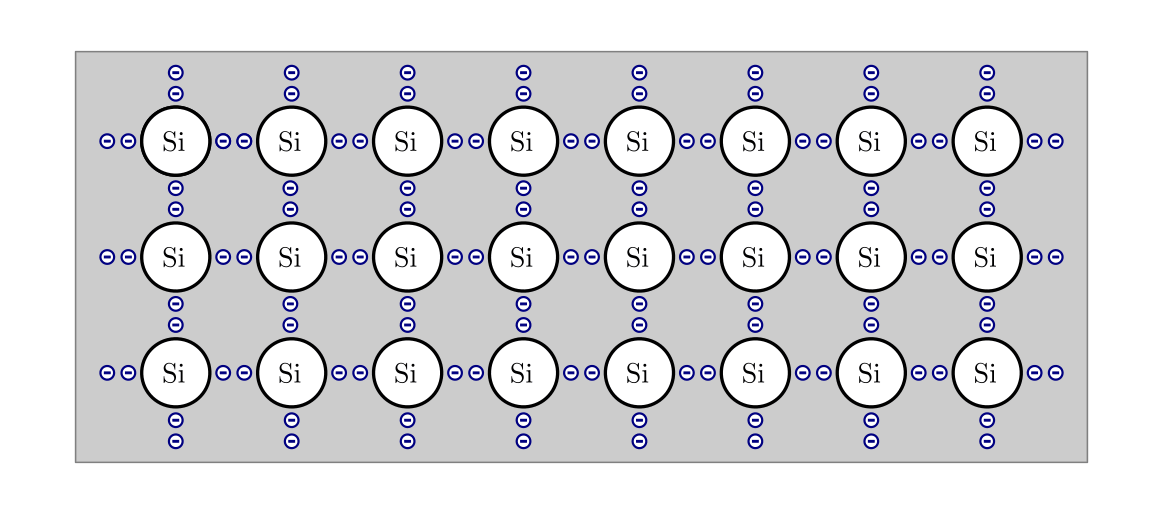
In reinen Halbleiter-Materialien sind – im Gegensatz zu elektrischen Leitern – im Grundzustand (fast) keine freien Ladungsträger verfügbar. Beispielsweise bilden im wohl typischsten Halbleiter-Element Silizium (und auch in Germanium) alle vier Valenzelektronen kovalente Bindungen mit den vier benachbarten Atomen aus. Nur durch ein zeitweises Herauslösen der Valenzelektronen mittels Licht, Wärme oder ausreichender elektrischer Spannung lässt sich ein Ladungstransport in einem reinen Halbleiter erreichen.
Elementare Halbleiter befinden sich im Periodensystem der Elemente in der vierten Hauptgruppe und besitzen eine chemische Wertigkeit von vier. Nach dem gleichen Bindungsprinzip sind ebenso sogenannte Verbindungshalbleiter möglich, bei denen die durchschnittliche chemische Wertigkeit vier beträgt:
- Bei Gallium-Arsenid
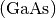 , einem III-V-Halbleiter, trägt jedes
Galliumatom drei und jedes Arsenatom fünf Valenzelektronen zu den kovalenten
Bindungen bei.
, einem III-V-Halbleiter, trägt jedes
Galliumatom drei und jedes Arsenatom fünf Valenzelektronen zu den kovalenten
Bindungen bei. - Bei Cadmium-Sulfid
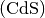 , einem II-VI-Halbleiter, trägt jedes
Cadmium-Atom zwei und jedes Schwefelatom sechs Valenzelektronen zu den
kovalenten Bindungen bei.[2]
, einem II-VI-Halbleiter, trägt jedes
Cadmium-Atom zwei und jedes Schwefelatom sechs Valenzelektronen zu den
kovalenten Bindungen bei.[2]
Bei höheren Temperaturen lösen sich Elektronen häufiger aus den kovalenten Bindungen heraus; der elektrische Widerstand eines Halbleiters wird daher – anders als bei Metallen – durch eine Erwärmung zunächst geringer. Bei noch stärkerer Erwärmung überwiegt jedoch wieder der stromhemmende Effekt der Atomschwingungen, wodurch der elektrische Widerstand wiederum stark ansteigt.
Durch ein gezieltes Einbringen von Fremdatomen kann die Leitfähigkeit eines Halbleiters beeinflusst werden.
Die  -Dotierung¶
-Dotierung¶
Bei einer  -Dotierung werden gezielt zusätzliche negativ geladene
Ladungsträger in einen Halbleiter eingefügt.
-Dotierung werden gezielt zusätzliche negativ geladene
Ladungsträger in einen Halbleiter eingefügt.
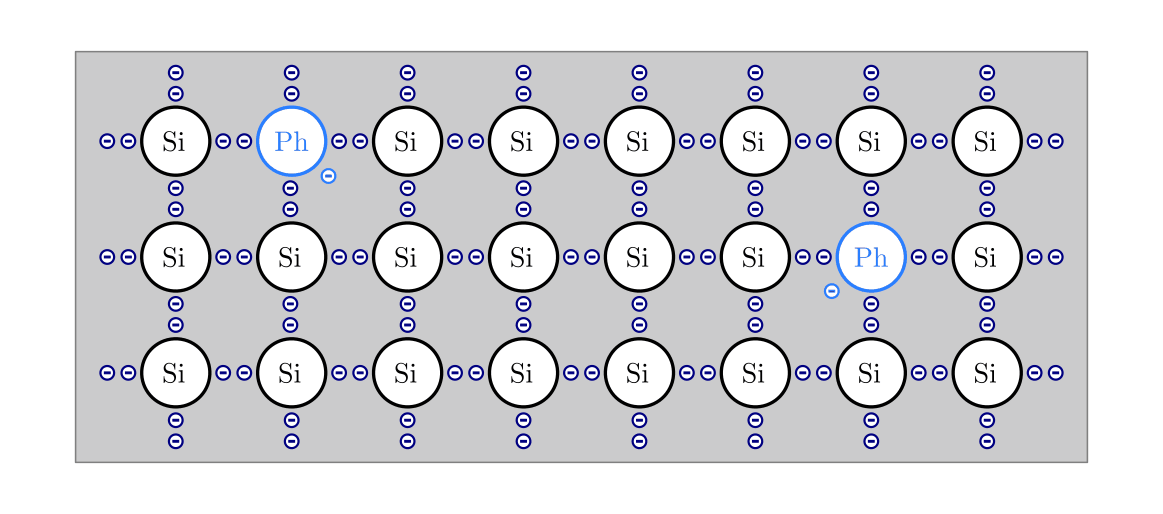
Bringt man ein chemisch fünfwertiges Atom (beispielsweise Phosphor) in einen Halbleiter-Kristall (beispielsweise Silicium) ein, so können nur vier der fünf Valenzelektronen des Phosphors kovalente Bindungen mit den benachbarten Atomen aufbauen. Das fünfte Valenzelektron bleibt ungebunden am Phosphoratom zurück und lässt sich verhältnismäßig leicht ablösen. Somit steht es im weiteren Sinn als ein „freier“ Ladungsträger für den elektrischen Strom zur Verfügung.
Typische chemisch fünfwertige Fremdatome („Donatoren“) sind beispielsweise
Phosphor 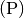 , Arsen
, Arsen 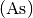 und Antimon
und Antimon
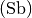 . In üblichen
. In üblichen  -Dotierungen wird ein Fremdatom auf
etwa
-Dotierungen wird ein Fremdatom auf
etwa 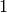 bis
bis 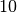 Millionen Halbleiter-Atome eingebracht. Der
Halbleiter bleibt durch die
Millionen Halbleiter-Atome eingebracht. Der
Halbleiter bleibt durch die  -Dotierung weiterhin elektrisch neutral.
-Dotierung weiterhin elektrisch neutral.
Die  -Dotierung¶
-Dotierung¶
Bei einer  -Dotierung werden gezielt zusätzliche positiv geladene
Ladungsträger in einen Halbleiter eingefügt.
-Dotierung werden gezielt zusätzliche positiv geladene
Ladungsträger in einen Halbleiter eingefügt.
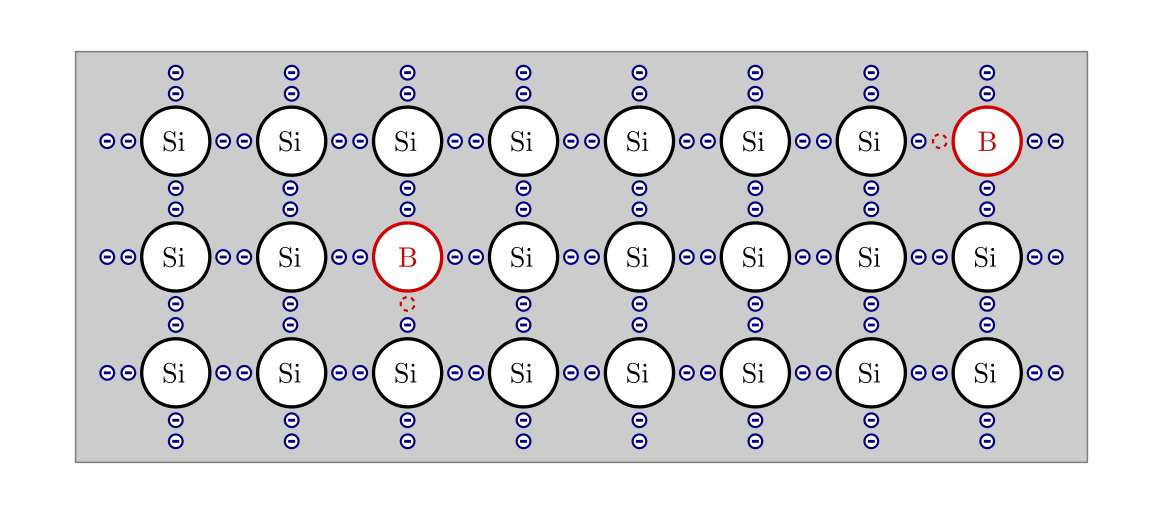
Bringt man ein chemisch dreiwertiges Atom (beispielsweise Bor) in einen Halbleiter-Kristall (beispielsweise Silicium) ein, so bleiben an den Bor-Atomen „Löcher“ oder „Defektstellen“ in den kovalenten Bindungen zurück. Jedes Bor-Atom ist zwar fest im Halbleiterkristall eingebunden, doch stellt jedes Loch einen freien Platz für benachbarte Valenzelektronen dar, der verhältnismäßig leicht besetzt werden kann. Springt ein Valenzelektron aus einer anderen kovalenten Bindung in die Defektstelle, so ist das Loch an eine neue Stelle weiter gewandert. Somit können die eingebrachten Löcher im weiteren Sinn als freie, einfach positiv geladene Ladungsträger angesehen werden.
Typische chemisch dreiwertige Fremdatome („Akzeptoren“) sind beispielsweise Bor
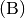 , Aluminium
, Aluminium 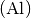 , Gallium
, Gallium 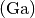 sowie
Indium
sowie
Indium 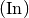 . In üblichen
. In üblichen  -Dotierungen wird ebenfalls ein
Fremdatom auf etwa
-Dotierungen wird ebenfalls ein
Fremdatom auf etwa 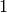 bis
bis 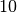 Millionen Halbleiter-Atome
eingebracht. Auch durch die
Millionen Halbleiter-Atome
eingebracht. Auch durch die  -Dotierung bleibt der Halbleiter
elektrisch neutral.
-Dotierung bleibt der Halbleiter
elektrisch neutral.
Der  -
- -Übergang¶
-Übergang¶
Verbindet man einen  - mit einem
- mit einem  -dotierten Halbleiterkristall,
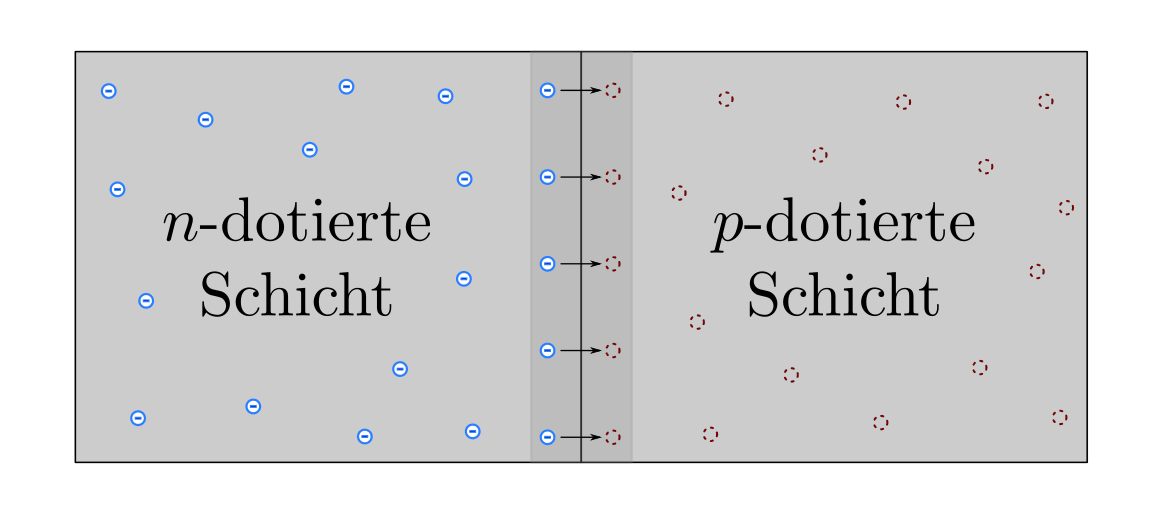
so bildet sich entlang der Verbindungslinie ein neutraler Übergangsbereich aus,
in der die zusätzlichen Elektronen der
-dotierten Halbleiterkristall,
so bildet sich entlang der Verbindungslinie ein neutraler Übergangsbereich aus,
in der die zusätzlichen Elektronen der  -dotierten Schicht die Löcher
der
-dotierten Schicht die Löcher
der  -dotierten Schicht auffüllen. Die paarweise Aufhebung von
Elektronen und Löchern wird als „Rekombination“, der entstehende Raumbereich als
„Raumladungszone“ oder „Grenzschicht“ bezeichnet.
-dotierten Schicht auffüllen. Die paarweise Aufhebung von
Elektronen und Löchern wird als „Rekombination“, der entstehende Raumbereich als
„Raumladungszone“ oder „Grenzschicht“ bezeichnet.
Innerhalb der Raumladungszone gleicht ein Halbleiter-Kristall mit
 -
- -Übergang einem Halbleiter ohne Dotierung, d.h. der
elektrische Widerstand der neutralen Grenzschicht ist gegenüber den restlichen
dotierten Bereichen deutlich erhöht.
-Übergang einem Halbleiter ohne Dotierung, d.h. der
elektrische Widerstand der neutralen Grenzschicht ist gegenüber den restlichen
dotierten Bereichen deutlich erhöht.
Die Dicke der neutralen Grenzschicht wird dadurch begrenzt, dass durch das
Abdriften der Elektronen in der (ursprünglich neutralen)  -dotierten
Schicht eine positive elektrische Ladungs-Anhäufung entsteht; in der
(ursprünglich ebenfalls neutralen)
-dotierten
Schicht eine positive elektrische Ladungs-Anhäufung entsteht; in der
(ursprünglich ebenfalls neutralen)  -dotierten Schicht baut sich
entsprechend durch die zusätzlichen Elektronen entlang der Grenzschicht eine
negative Ladungs-Anhäufung auf.[3] Da sich durch die Ladungstrennung eine
elektrische Spannung zwischen beiden Schichten aufbaut, kommt es schließlich zu
einem Gleichgewicht zwischen dem (thermisch bedingten) Driften der Elektronen
und der entgegengesetzt wirkenden „Drift-Spannung“.
-dotierten Schicht baut sich
entsprechend durch die zusätzlichen Elektronen entlang der Grenzschicht eine
negative Ladungs-Anhäufung auf.[3] Da sich durch die Ladungstrennung eine
elektrische Spannung zwischen beiden Schichten aufbaut, kommt es schließlich zu
einem Gleichgewicht zwischen dem (thermisch bedingten) Driften der Elektronen
und der entgegengesetzt wirkenden „Drift-Spannung“.
In Silizium-Kristallen beträgt die Drift-Spannung rund ![U_{\mathrm{D, Si}}
\approx \unit[0,7]{V}](../_images/math/38dffe338dd0c2f215405c5908c6814a12cc096a.png) , in Germanium-Kristallen rund
, in Germanium-Kristallen rund ![U_{\mathrm{D, Ge}}
\approx \unit[0,3]{V}](../_images/math/2d838e786384f6145f6eaceadc69fca4a6075a63.png) . Die Dicke der Raumladungszone hat bei typischen
Dotierungen eine Größenordnung von
. Die Dicke der Raumladungszone hat bei typischen
Dotierungen eine Größenordnung von ![\unit[0,001]{mm}](../_images/math/a6949fea97b386d3bde899ac1349e5a754066d72.png) .
.
Durchlass-Richtung und Sperr-Richtung
Legt man an einen Halbleiter-Kristall mit  -
- -Übergang von außen
eine elektrische Spannung an, so lässt sich die Dicke seiner Grenzschicht und
damit auch seine elektrische Leitfähigkeit gezielt beeinflussen.
-Übergang von außen
eine elektrische Spannung an, so lässt sich die Dicke seiner Grenzschicht und
damit auch seine elektrische Leitfähigkeit gezielt beeinflussen.
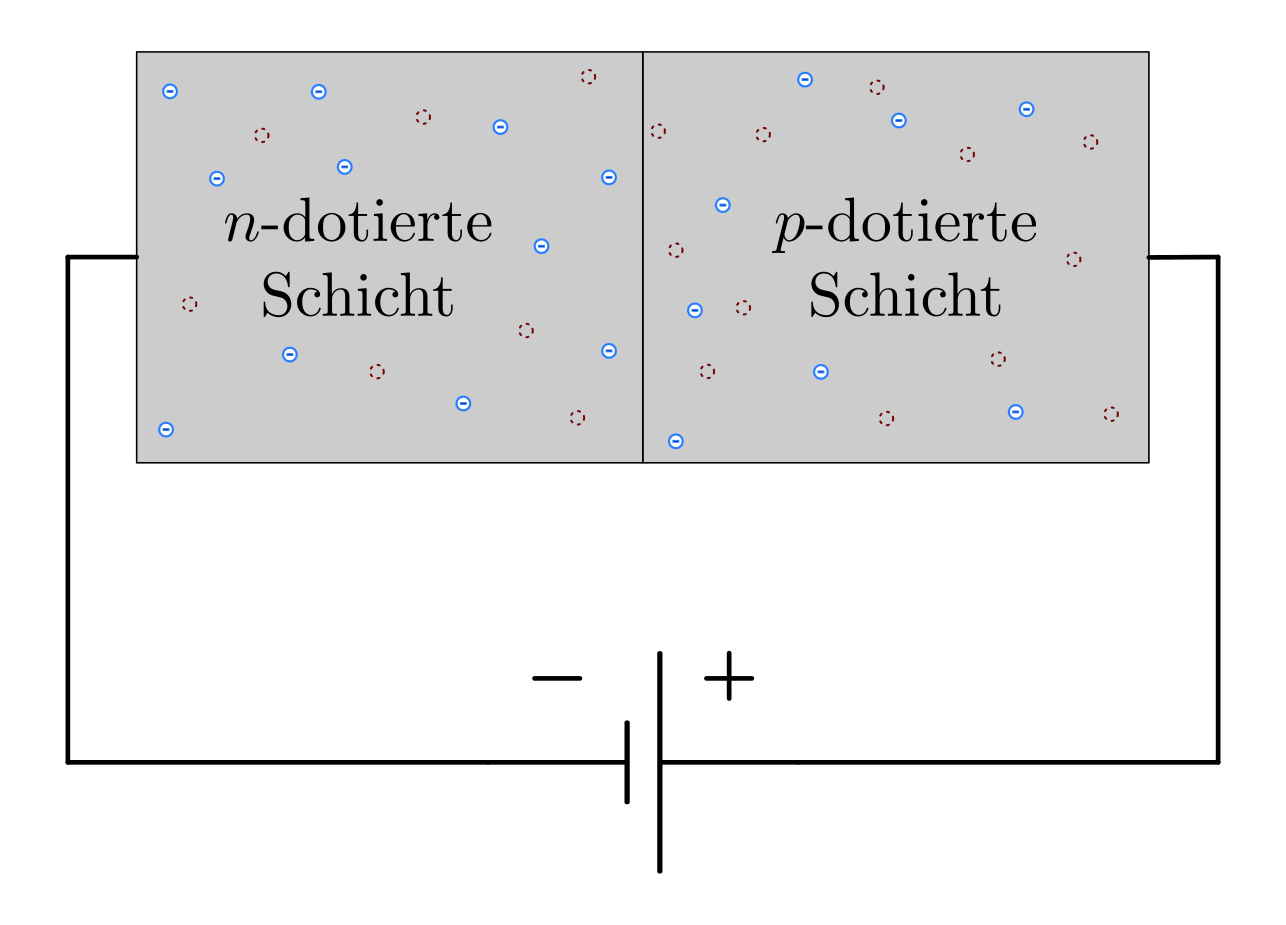
- Verbindet man die
 -dotierte Schicht mit dem Plus- und die
-dotierte Schicht mit dem Plus- und die
 -dotierte Schicht mit dem Minus-Pol einer Stromquelle
(„Sperr-Richtung“), so werden die Elektronen und Löcher von der Grenzschicht
weg beziehungsweise an den Rand des Halbleiter-Kristalls hingezogen. Die
neutrale Raumladungszone wird dadurch vergrößert, der elektrische Widerstand
steigt stark an.
-dotierte Schicht mit dem Minus-Pol einer Stromquelle
(„Sperr-Richtung“), so werden die Elektronen und Löcher von der Grenzschicht
weg beziehungsweise an den Rand des Halbleiter-Kristalls hingezogen. Die
neutrale Raumladungszone wird dadurch vergrößert, der elektrische Widerstand
steigt stark an.
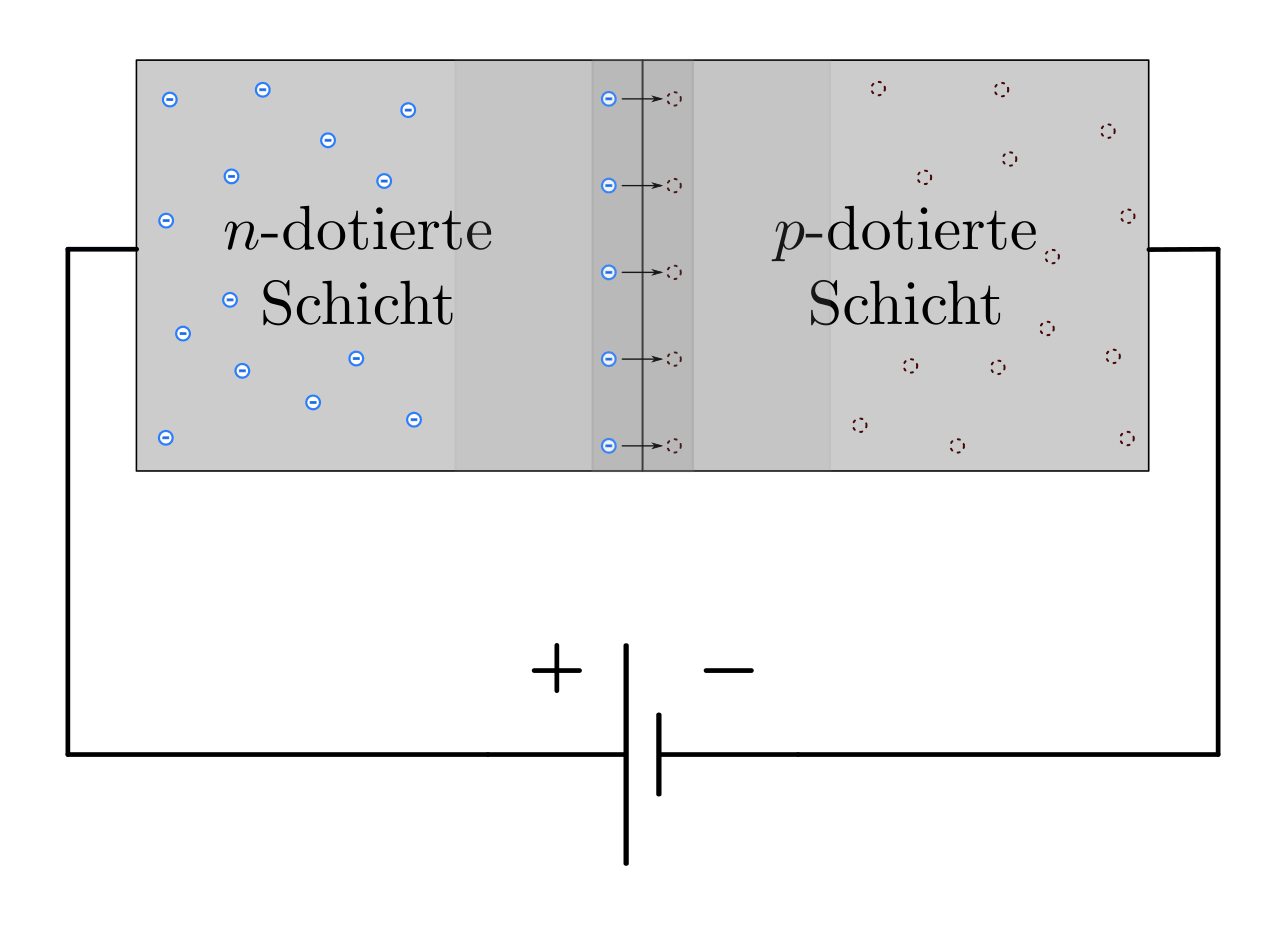
- Verbindet man die
 -dotierte Schicht mit dem Minus- und die
-dotierte Schicht mit dem Minus- und die
 -dotierte Schicht mit dem Plus-Pol einer Stromquelle
(„Durchlass-Richtung“), so werden an der
-dotierte Schicht mit dem Plus-Pol einer Stromquelle
(„Durchlass-Richtung“), so werden an der  -Schicht kontinuierlich
Elektronen nachgeliefert. Ist die angelegte Spannung größer als die
Drift-Spannung im Kristall, so können sich die zusätzlichen Elektronen im
Kristall ausbreiten. Die Elektronen und Löcher verteilen sich, ähnlich wie
gelöste Ionen im Wasser, über den gesamten Kristall und tragen gleichermaßen
zum Ladungstransport bei.
-Schicht kontinuierlich
Elektronen nachgeliefert. Ist die angelegte Spannung größer als die
Drift-Spannung im Kristall, so können sich die zusätzlichen Elektronen im
Kristall ausbreiten. Die Elektronen und Löcher verteilen sich, ähnlich wie
gelöste Ionen im Wasser, über den gesamten Kristall und tragen gleichermaßen
zum Ladungstransport bei.
In der Elektronik werden  -
- -Übergänge in
Halbleiter-Bauelementen verwendet. Ein einzelner
-Übergänge in
Halbleiter-Bauelementen verwendet. Ein einzelner  -
- -Übergang
erfüllt die Funktion einer Diode. Doppelte beziehungsweise dreifache
-Übergang
erfüllt die Funktion einer Diode. Doppelte beziehungsweise dreifache
 -
- -Übergänge finden in Transistoren und
Triacs Anwendung.
-Übergänge finden in Transistoren und
Triacs Anwendung.
Isolatoren¶
Isolatoren sind Stoffe, in denen sich Ladungen (fast) überhaupt nicht bewegen können. Bekannte Beispiele hierfür sind Gummi, Porzellan, Glas, Diamant, destilliertes Wasser und Luft. Alle diese Stoffe haben gemeinsam, dass in ihnen weder Ionen noch schwach gebundene Elektronen für den Ladungstransport zur Verfügung stehen; alle Elektronen sind fest in chemischen Bindungen verankert.
Bei extrem hohen Spannungen (einigen Kilo- bis Megavolt) können dennoch kurzzeitig Elektronen aus den Stoffbindungen entrissen werden. Die Folge ist ein „Durchschlag“-Strom (beispielsweise ein Blitz), bei dem in sehr kurzer Zeit sehr viel Energie transportiert wird. Da die Schäden für Menschen, Tiere, Pflanzen und elektronische Geräte entsprechend groß ausfallen können, werden beispielsweise hochgelegene Leitungen und Gebäude mit Überspannungs- beziehungsweise Blitzableitern ausgestattet.
Vakuum
Normalerweise sind Elektronen in Molekülen oder metaillischen Festkörpern gebunden. Unter verschiedenen Bedingungen können Elektronen diese Bindungen allerdings verlassen:
- Trifft ausreichend energiereiches Licht auf einen Festkörper, so können durch die Lichteinwirkung Elektronen aus den Festkörper-Bindungen herausgelöst werden („Photo-Effekt“).
- Bei ausreichend hohen Temperaturen lösen sich Elektronen aus Metallen heraus („Glühemission“).
Die den Elektronen zugeführte Licht- beziehungsweise Wärme-Energie muss groß genug sein, um die Bindungsenergie der Elektronen zu überwinden; die restliche zugeführte Energie verbleibt als kinetische Energie bei den Elektronen.
Im Vakuum erfahren freie Elektronen keine Stöße mit anderen Objekten. Beschleunigt man sie durch Anlegen einer elektrischen Spannung, so können sie in eine bestimmte Richtung gelenkt und auf hohe Geschwindigkeitswerte beschleunigt werden. Auf diesem Prinzip beruhen beispielsweise Elektronenröhren.
Exkurs: Driftgeschwindigkeit von Elektronen¶
Drückt man auf einen Lichtschalter, so leuchtet quasi „sofort“ die Lampe auf. Die zunächst nur an den Leiter-Enden des noch offenen Schalters anliegende Spannung muss also unmittelbar nach dem Schließen des Schalters auch an der Lampe anliegen.
Tatsächlich breiten sich elektrische Felder mit Lichtgeschwindigkeit aus. Man kann sich das in einem einfachen Vergleich wie einen bereits komplett mit Wasser gefüllten Schlauch vorstellen: Füllt man an einem Ende zusätzlich Wasser hinein, so fließt es sofort am anderen Ende über. Dazu muss allerdings das neu hineinfließende Wasser nicht erst den ganzen Weg durch den Schlauch zurücklegen.
Wie schnell bewegen sich also Elektronen in einem Leiter? Man kann für eine
Abschätzung von der so genannten Elektronendichte  des jeweiligen
Leitermaterials ausgehen; diese gibt an, wie viele freie Elektronen sich in
einem Material je Raumeinheit befinden. Für Kupfer beträgt dieser Wert
beispielsweise
des jeweiligen
Leitermaterials ausgehen; diese gibt an, wie viele freie Elektronen sich in
einem Material je Raumeinheit befinden. Für Kupfer beträgt dieser Wert
beispielsweise ![n_{\mathrm{Cu}} = \unit[8,47 \cdot 10^{19}]{\frac{1}{mm^3}}](../_images/math/4b5adab5f752fc64b378c4fae5229d6a7042a3c9.png) .
.
Jedes Elektron trägt genau eine Elementarladung ![q_{\mathrm{e}} =
\unit[1,6022 \cdot 10^{-19}]{C}](../_images/math/ae600819c9005dc86e138a3083f451f0b3aea50b.png) . Für die bewegliche Ladungsmenge in einem
Leiterstück gilt also:
. Für die bewegliche Ladungsmenge in einem
Leiterstück gilt also:
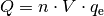
Das Volumen  des Leiterstücks kann wiederum als Produkt aus seiner
Querschnittsfläche
des Leiterstücks kann wiederum als Produkt aus seiner
Querschnittsfläche  und seiner Länge
und seiner Länge  geschrieben werden. Es
gilt somit:
geschrieben werden. Es
gilt somit:
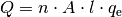
Ein elektrischer Strom  entspricht einer sich zeitlich bewegenden
Ladungsmenge, es ist also
entspricht einer sich zeitlich bewegenden
Ladungsmenge, es ist also 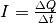 . Wenn das
Leiterstück an allen Stellen aus dem gleichen Material besteht und
eine konstante Querschnittsfläche hat, so ist die Länge
. Wenn das
Leiterstück an allen Stellen aus dem gleichen Material besteht und
eine konstante Querschnittsfläche hat, so ist die Länge  die einzige
zeitlich veränderliche Größe. Eine zeitliche Änderung einer Strecke
ist allerdings nichts anderes als eine Geschwindigkeit; man kann also schreiben:
die einzige
zeitlich veränderliche Größe. Eine zeitliche Änderung einer Strecke
ist allerdings nichts anderes als eine Geschwindigkeit; man kann also schreiben:
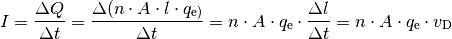
Die Drift-Geschwindigkeit 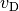 gibt an, wie schnell sich ein
bestimmtes Elektronen-Volumen, das man sich beispielsweise gefärbt vorstellen
könnte, durch den Leiter „hindurch schiebt“. Löst man die obige Gleichung nach
gibt an, wie schnell sich ein
bestimmtes Elektronen-Volumen, das man sich beispielsweise gefärbt vorstellen
könnte, durch den Leiter „hindurch schiebt“. Löst man die obige Gleichung nach
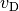 auf, so erhält man:
auf, so erhält man:
(1)¶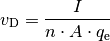
Diese Gleichung enthält neben der Naturkonstanten 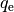 und der
Materialkonstanten
und der
Materialkonstanten  nur die Querschnittsfläche
nur die Querschnittsfläche  des Leiters
sowie die fließende Stromstärke
des Leiters
sowie die fließende Stromstärke  als leicht messbare Größen.
als leicht messbare Größen.
Beispiel:
Wie groß ist die Driftgeschwindigkeit der Elektronen in einer gewöhnlichen Kupfer-Leitung mit einer Querschnittsfläche von
![A=\unit[1,5]{mm^2}](../_images/math/7f2a1a2b47cb00a3b86232958e3c5ea98429f53d.png) ,
wenn eine Stromstärke von
,
wenn eine Stromstärke von ![I=\unit[5,0]{A}](../_images/math/6cde9fa254424939db25011ef89a4a4637431480.png) im Stromkreis auftritt?
im Stromkreis auftritt?Für Kupfer beträgt die Elektronendichte
![n_{\mathrm{Cu}} =
\unit[8,47 \cdot 10^{19}]{\frac{1}{mm^3}}](../_images/math/f30914b7bd934edd260f7ee72d55ec727757f0ac.png) ; somit erhält man nach der Formel
(1) für die Driftgeschwindigkeit:
; somit erhält man nach der Formel
(1) für die Driftgeschwindigkeit:![v_{\mathrm{D}} = \frac{I}{n \cdot A \cdot q_{\mathrm{e}}} =
\frac{\unit[5,0]{A}}{\unit[8,47 \cdot 10^{19}]{\frac{1}{mm^3}} \cdot
\unit[1,5]{mm^2} \cdot \unit[1,6022 \cdot 10^{-19}]{C}} \approx
\unit[0,246]{\frac{mm}{s}}](../_images/math/5ef3bf236a7999f8d9a8b1544135dd92f0f4551d.png)
Die Einheit ergibt sich wegen
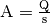 .
.
Die Driftgeschwindigkeit der Elektronen in einem metallischen Leiter ist somit im Vergleich zur Ausbreitungs-Geschwindigkeit des elektrischen Feldes (Lichtgeschwindigkeit) nur sehr gering.
Anmerkungen:
| [1] | Die Leitfähigkeit eines Metalls ist rund 10 Milliarden (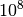 )
mal höher als die eines Halbleiters und rund 100 Billionen ( )
mal höher als die eines Halbleiters und rund 100 Billionen (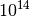 )
mal höher als die eines Isolators! )
mal höher als die eines Isolators! |
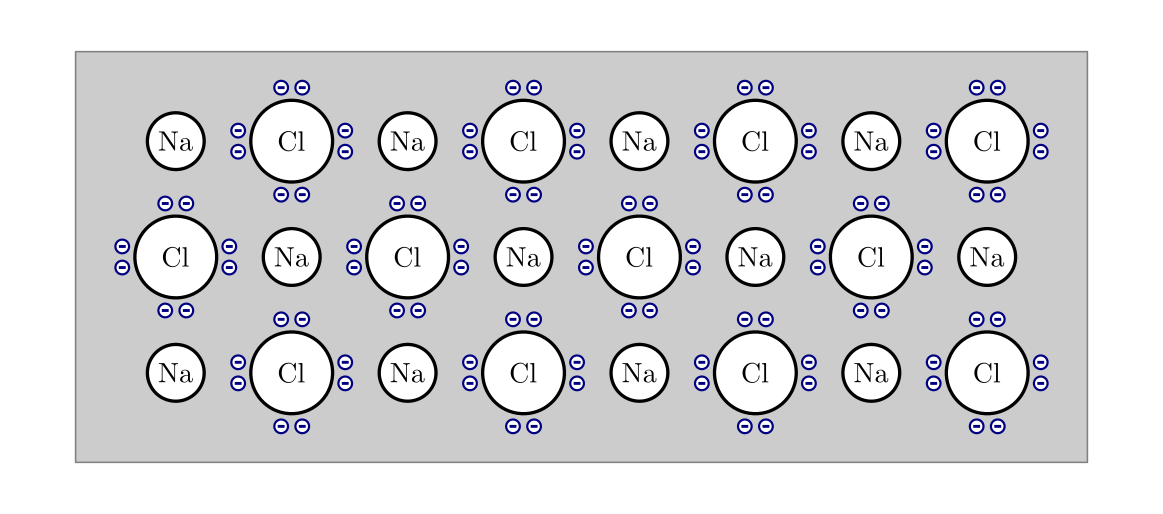
| [2] | Je deutlicher Halbleiter-Verbindungen von der elementaren IV-IV-Bindung abweichen, desto größer wird auch der ionische Anteil an den kovalenten Bindungen. I-VII-Verbindungen (Salze) haben rein ionischen Charakter und zählen aufgrund der Festigkeit der Bindungen zu den elektrischen Isolatoren. |
| [3] | Die fest verankerten Atomrümpfe und damit die Protonen der fünf- beziehungsweise dreiwertigen Donator- beziehungsweise Akzeptor-Atome bleiben in den jeweiligen Schichten zurück. |
Hinweis
Zu diesem Abschnitt gibt es Experimente.