Mechanische Leistung¶
Mechanische Arbeit kann unterschiedlich schnell verrichtet werden. Die mechanische Leistung (umgangssprachlich auch „Arbeitstempo“ genannt) gibt an, wie schnell mechanische Arbeit verrichtet wird.
Definition:
(1)¶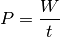
Einheit:
Die Leistung wird (zu Ehren des Ingenieurs James Watt) in Wattangegeben. Eine Leistung von einem Watt entspricht einer in einer Sekunde geleisteten Arbeit von einem Joule:
![\unit[1]{W} = \frac{\unit[1]{J}}{\unit[1]{s}}](../../_images/math/363cbc387c1f2b6c5e4a889e5ed20d50142ae97e.png)
Beispiel:
Zwei Kräne ziehen jeweils eine Palette mit Steinen, die einer Gewichtskraft
![F_{\mathrm{G}} = \unit[4\,000]{N}](../../_images/math/e3490fb3c8847eae0ca9f5f63f7cd086f6136657.png) entspricht, auf ein
entspricht, auf ein ![\unit[5]{m}](../../_images/math/7f0402ed54213fe37ab62a24b9bd6191d76b2a9e.png) hohes
Gerüst. Der eine Kran braucht für diese Arbeit eine Zeit von
hohes
Gerüst. Der eine Kran braucht für diese Arbeit eine Zeit von ![t
_1 = \unit[10]{s}](../../_images/math/4d0d9d97db40e7ff26cbe900b7a17b8b860ba71b.png) , der andere Kran benötigt hingegen
, der andere Kran benötigt hingegen ![t
_2 = \unit[20]{s}](../../_images/math/59e7f253c34ccca2fa10fcd97244463630de4129.png) . Damit können die Leistungen
. Damit können die Leistungen 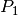 und
und
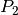 der beiden Kräne berechnet werden:
der beiden Kräne berechnet werden:![P_1 = \frac{W_{\mathrm{Hub} }}{t_1} = \frac{F_{\mathrm{G}} \cdot h}{t_1} =
\frac{\unit[4\,000]{N} \cdot \unit[5]{m}}{\unit[10]{s}} =
\frac{\unit[20\,000]{J}}{\unit[10]{s}} = \unit[2\,000]{W} \\[5pt]
P_2 = \frac{W_{\mathrm{Hub} }}{t_2} = \frac{F_{\mathrm{G}} \cdot h}{t_2} =
\frac{\unit[4\,000]{N} \cdot \unit[5]{m}}{\unit[20]{s}} =
\frac{\unit[20\,000]{J}}{\unit[20]{s}} = \unit[1\,000]{W}](../../_images/math/389156a2c7944f56101c41038857af1ce33545d2.png)
Da der erste Kran die Arbeit in der halben Zeit verrichtet, ist seine Leistung (sein „Arbeitstempo“) doppelt so hoch wie die des zweiten Kranes.
| Spielzeugmotor | ![\phantom{0}3 \text{ bis } \unit[12]{W}](../../_images/math/7c7628f7b1ce329069a0d39f600be50d6e7713ef.png) |
| Mensch (Dauerleistung) | ![75 \text{ bis } \unit[100]{W}](../../_images/math/a9038e21adff7a0202ec26161ffd9d2fb50cd89d.png) |
| Bohrmaschine | ![300 \text{ bis } \unit[1\,000]{W}](../../_images/math/8ba473cda39c4f0deea421dca45d6183f9fcd13a.png) |
| Motorrad | ![\text{Ca. } \unit[15\,000]{W}](../../_images/math/7b3b75041d0a3acbdd03c711c959bfc626328c49.png) |
| PKW | ![\text{Ca. } \unit[55\,000]{W}](../../_images/math/65a1b24b96e5bdb3672d7b00bb66b77fbedb6667.png) |
| LKW | ![\text{Ca. } \unit[250\,000]{W}](../../_images/math/d1b82aaaea1c35eae96983840767684172a8a033.png) |
| Elektro-Lokomotive | ![\text{Ca. } \unit[5\,000\,000]{W}](../../_images/math/1d31b2d9b4cbc66cf57ea3026699334cdd209eef.png) |
| Verkehrsflugzeug | ![\text{Ca. } \unit[35\,000\,000]{W}](../../_images/math/5c196ad0e7165e7725bd2bc9576b8129770cb871.png) |
| Passagierschiff | ![\text{Ca. } \unit[40\,000\,000]{W}](../../_images/math/7c8d08b58dc3fa1fe4e724b3fd9c36a54ba4e0ad.png) |
| Weltraum-Rakete | ![\text{Ca. } \unit[75\,000\,000\,000]{W}](../../_images/math/6a5318e618e8ef72bc946c584af480965bd30831.png) |
| Blitz | ![\text{Ca. } \unit[500\,000\,000\,000]{W}](../../_images/math/b779c2de0215311070b6f582cdda6e35acf0781b.png) |
Die mechanische Leistung, die ein Mensch über einen langen Zeitraum aufrecht
erhalten kann, liegt bei etwa ![\unit[100]{W}](../../_images/math/7d1c0c605c226d5b4e302a0cdbe6f6494713f18a.png) . Kurzzeitig kann ein gut
trainierter Mensch auch eine Leistung in der Größenordnung von
. Kurzzeitig kann ein gut
trainierter Mensch auch eine Leistung in der Größenordnung von
![\unit[1\,000]{W}](../../_images/math/70aeb040844d99cfae947ac27bb846322dfdde70.png) erreichen. Große Leistungsmengen werden nach wie vor
häufig in Pferdestärken
erreichen. Große Leistungsmengen werden nach wie vor
häufig in Pferdestärken 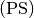 anstelle in Kilowatt
anstelle in Kilowatt
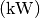 angegeben.
angegeben.
![\unit[1]{kW} = \unit[1\,000]{W} \\
\unit[1]{PS} \approx \unit[735,5]{W}](../../_images/math/dfe3c4a7ffdf06ac00e1f8cb9b8a8fdf4f29ad97.png)
Eine weitere nützliche Formel erhält man, wenn man in der Definition
(1) für die Arbeit 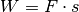 schreibt. Für die
Leistung
schreibt. Für die
Leistung 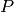 gilt damit:
gilt damit:
(2)¶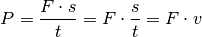
Gemäß dieser Gleichung ist zum Beispiel eine höhere Leistung nötig, um einen Gegenstand bei einer konstant wirkenden Reibung mit höherer Geschwindigkeit zu ziehen.
Leistung von rotierenden Objekten
Vorgänge, bei denen Verschiebungen (Translationen) oder Drehungen (Rotationen)
von Objekten stattfinden, lassen sich durch mathematisch ähnliche Gleichungen
beschreiben. Das Äquivalent zur Kraft  ist bei Rotationen das
Drehmoment
ist bei Rotationen das
Drehmoment 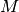 , das Äquivalent zur Geschwindigkeit
, das Äquivalent zur Geschwindigkeit
 ist die Winkelgeschwindigkeit
ist die Winkelgeschwindigkeit
 . Ersetzt man in der obigen Formel (2) die
jeweiligen Größen, so erhält man folgende Formel:
. Ersetzt man in der obigen Formel (2) die
jeweiligen Größen, so erhält man folgende Formel:
(3)¶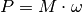
Ein Motor kann somit eine bestimmte Leistung entweder durch eine große Drehzahl
oder ein großes Drehmoment erreichen; ist die Winkelgeschwindigkeit
 gleich Null, so ist auch die mechanische Leistung des Motors
gleich Null, egal wie hoch sein Drehmoment ist.
gleich Null, so ist auch die mechanische Leistung des Motors
gleich Null, egal wie hoch sein Drehmoment ist.
Anmerkungen:
| [1] | Das Symbol 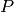 für die Leistung leitet sich vom englischen Wort
„Power“ ab. für die Leistung leitet sich vom englischen Wort
„Power“ ab. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

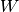 und der Zeit
und der Zeit  , in der sie verrichtet wird.
, in der sie verrichtet wird.