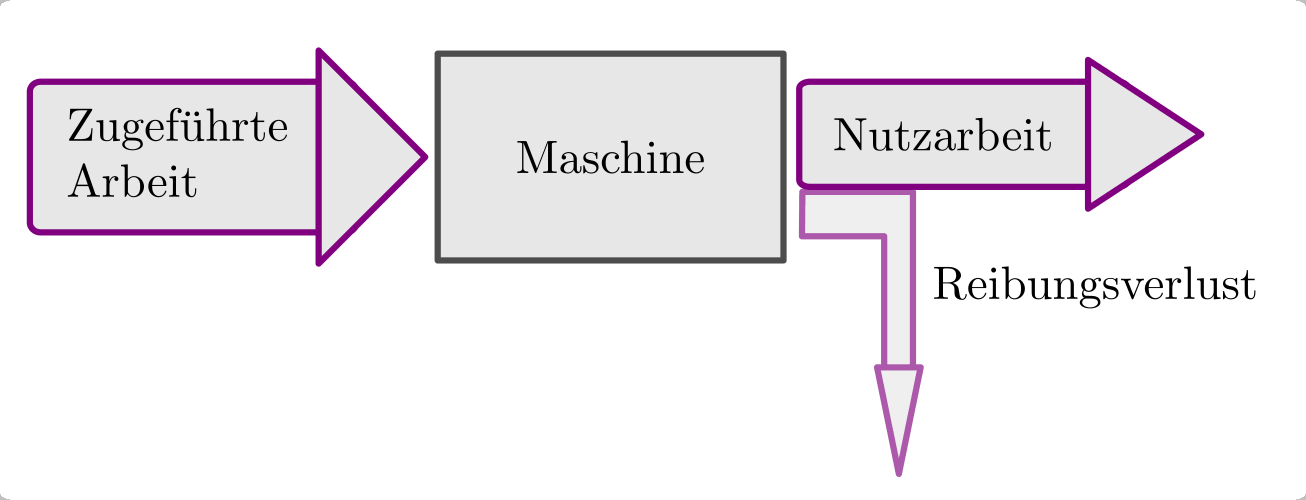
Wirkungsgrad¶
Sofern bei einem mechanischen Prozess die stets auftretende Reibung sehr klein gehalten werden kann, so ist es möglich, sie bei der Formulierung von physikalischen Gesetzen unberücksichtigt zu lassen. Bei genauer Betrachtung zeigt sich allerdings, dass die von einer mechanischen Einrichtung aufgenommene Arbeit stets größer ist als die von ihr abgegebene Arbeit. Es scheint also Arbeit verloren gegangen zu sein, der Satz von der Erhaltung der mechanischen Arbeit scheint somit seine Geltung zu verlieren.
Tatsächlich verschwindet die verrichtete Arbeit allerdings nicht, sondern es wird stets eine entsprechend große Menge an Reibungsarbeit verrichtet. Das Gesetz von der Erhaltung der mechanischen Arbeit kann – unter Berücksichtigung der Reibung – somit folgendermaßen formuliert werden:[1]
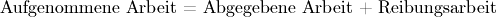
Definition:
Das Verhältnis aus der abgegebenen Arbeitund der aufgenommenen Arbeit
wird Wirkungsgrad
einer mechanischen Einrichtung genannt:
(1)¶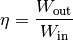
Einheit:
Als Verhältniszahl hat der Wirkungsgrad keine Einheit. Er ist umso größer, je geringer die Reibungsarbeit ist. Ist überhaupt keine Reibung vorhanden, so ergibt sich der Wert, da in diesem Fall der Zähler und der Nenner auf der rechten Seite der Gleichung übereinstimmen.
Da sich – abgesehen von in Vakuum stattfindenden Prozessen – Reibung niemals
komplett beseitigen lässt, gibt es keine mechanische Einrichtung mit einem
Wirkungsgrad 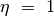 . Durch gutes Ölen und Schmieren ist es allerdings
möglich, diesen Wert zumindest annähernd zu erreichen. Ein hoher Wirkungsgrad,
der nur geringfügig kleiner als
. Durch gutes Ölen und Schmieren ist es allerdings
möglich, diesen Wert zumindest annähernd zu erreichen. Ein hoher Wirkungsgrad,
der nur geringfügig kleiner als 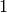 ist, bedeutet, dass der größte Teil
der aufgenommenen Arbeit als abgegebene mechanische Arbeit wirksam ist.
ist, bedeutet, dass der größte Teil
der aufgenommenen Arbeit als abgegebene mechanische Arbeit wirksam ist.
Besteht eine mechanische Einrichtung aus mehreren Komponenten, die jeweils die
Wirkungsgrade 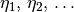 haben, so ergibt sich für den
Gesamt-Wirkungsgrad
haben, so ergibt sich für den
Gesamt-Wirkungsgrad 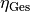 der Anlage:
der Anlage:
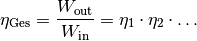
Der Gesamt-Wirkungsgrad einer mechanischen Einrichtung ist wegen 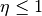 somit kleiner als der Wirkungsgrad der am wenigsten effizienten Komponente.
somit kleiner als der Wirkungsgrad der am wenigsten effizienten Komponente.
Anmerkungen:
| [1] | Eine noch allgemeinere Formulierung dieser Aussage stellen die so genannten Hauptsätze der Wärmelehre dar. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.