Dynamik¶

Mechanische Kräfte¶

Die folgenden Aufgaben beziehen sich auf den Abschnitt Mechanische Kräfte.

(*) Wieso ist es gefährlich, beim Fahrradfahren mit höherer Geschwindigkeit die Hinter- mit der Vorderbremse zu verwechseln? Welche Rolle spielt dabei die Masse des Radfahrers beziehungsweise seine (Massen-)Trägheit?

Lösung

(*) Wenn eine Straßenbahn vor dem Anhalten allmählich abbremst, erfahren die Fahrgäste beim Anhalten einen Ruck nach hinten. Wie ist das zu erklären?

Lösung

(*) Um einen Körper in Bewegung zu versetzen, ist stets eine Kraft notwendig. Ist der Körper nicht verformbar („starr“), so haben gleich gerichtete Zug- und Druckkräfte eine gleiche Wirkung. Erkläre dies am Beispiel eines Einkaufswagens, der gezogen oder geschoben wird. Wo befindet sich jeweils der Angriffspunkt, wo die Wirkungslinie der Kraft?

Lösung

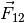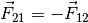(*) Zu jeder Kraft $\vec{F}_{12}$ gibt es stets eine gleich große, in die umgekehrte Richtung wirkende Gegenkraft $\vec{F}_{21} = - \vec{F}_{12}$ . Finde in der folgenden Abbildung zueinander gehörende Kraft-Gegenkraft-Paare und zeichne Kraftpfeile mit passenden Richtungen ein.

SVG: Kraft und Gegenkraft 1
Lösung

Zusammenwirken mehrerer Kräfte¶

Die folgenden Aufgaben beziehen sich auf den Abschnitt Zusammenwirken mehrerer Kräfte.

(*) Ein Kind mit einer Masse von $m = \unit[30]{kg}$ sitzt auf einer Schaukel. Welche Kraft wirkt auf die beiden Seile der Schaukel?

Lösung

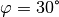(**) Zwei Kinder ziehen einen Schlitten mit den beiden Kräften $F_1 = F_2 = \unit[40]{N}$ . Die Kräfte wirken in unterschiedlicher Richtung, der Winkel gegenüber der zum Schlitten senkrecht verlaufenden Linie beträgt jeweils $\varphi = 30\degree$ . Welche resultierende Gesamtkraft ergibt sich?

SVG: Kraftaddition Schlitten
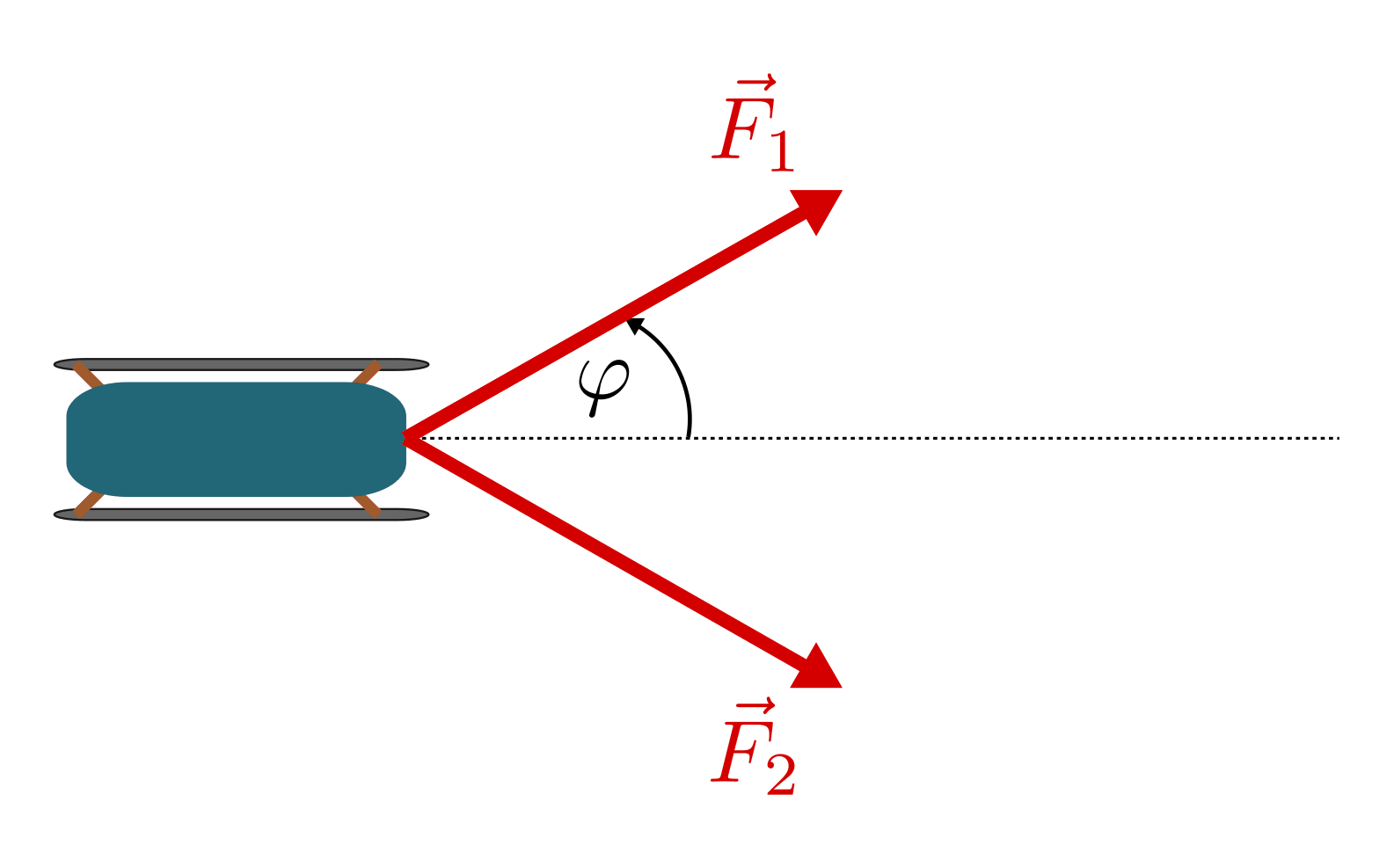
Hinweis: Die Aufgabe lässt sich graphisch (mit Hilfe eines Kräfte-Parallelogramms) oder rechnerisch lösen.

Lösung

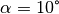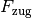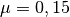(*) Ein Schlitten mit Kind (Gesamt-Gewichtskraft: $\unit[500]{N}$ ) wird von einem Erwachsenen gezogen. Das Zugseil schließt dabei mit der Horizontalen einen Winkel von $\alpha = 10\degree$ ein. Wie groß ist die nötige Zugkraft $F_{\mathrm{zug}}$ , wenn die Reibungszahl zwischen Schlitten und Schnee $\mu = 0,15$ beträgt?

SVG: Kraftzerlegung am Beispiel eines Schlittens
Lösung

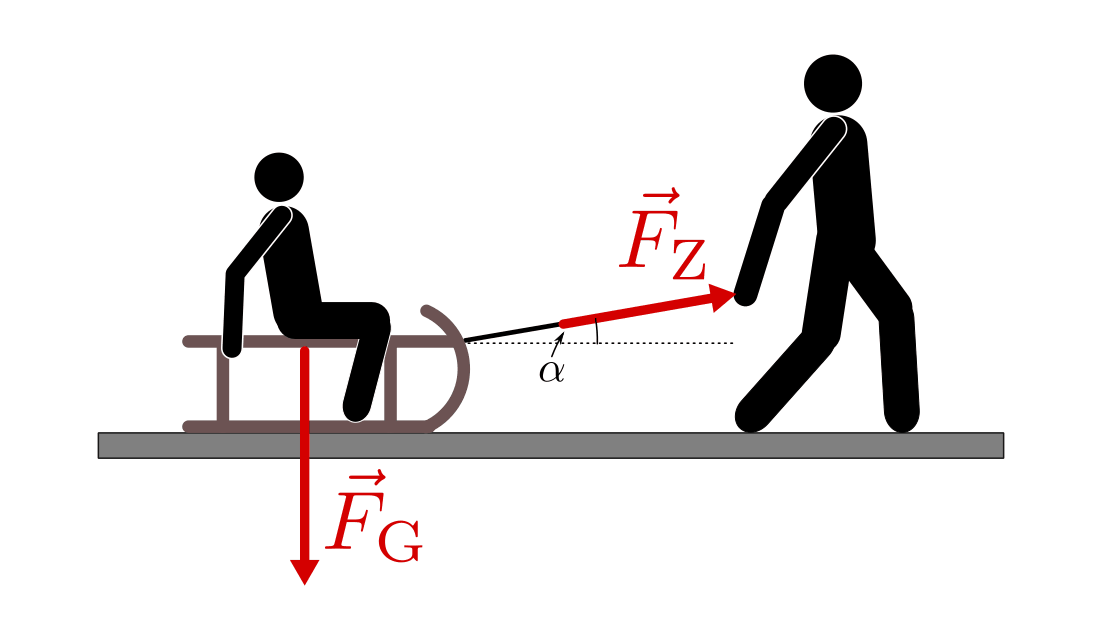
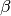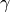(**) Welche Winkel $\alpha$ , $\beta$ und $\gamma$ müssen drei an einem gemeinsamen Punkt angreifende Kräfte $F_1 = \unit[50]{N}$ , $F_2 = \unit[70]{N}$ und $F_3 = \unit[90]{N}$ einschließen, damit zwischen ihnen ein Kräftegleichgewicht herrscht?

Lösung

(*) Eine Straßenlaterne mit einer Gewichtskraft von $F_{\mathrm{G}} = \unit[50]{N}$ wird von zwei Stahlseilen in einem Winkel von 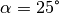$\alpha = 25 \degree$ gehalten. Wie groß ist die Kraft im linken bzw. im rechten Seilstück?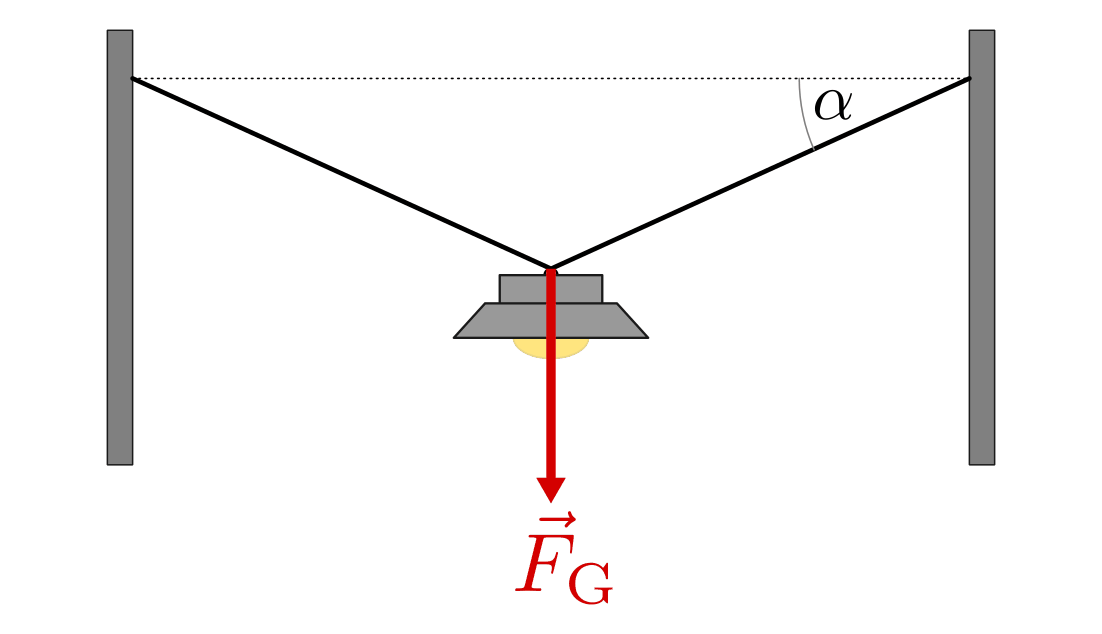

SVG: Kraftzerlegung am Beispiel einer Straßenlaterne
Lösung

(**) Eine Straßenlaterne mit einer Gewichtskraft von $F_{\mathrm{G}} = \unit[50]{N}$ wird asymmetrisch von zwei Stahlseilen. Der Aufhängepunkt der Lampe befindet sich jeweils $h=\unit[1,0]{m}$ unterhalb der Befestigungsstellen der Seile an den tragenden Wänden; der Abstand der Lampe zur linken Wand beträgt $l_1 = \unit[5,0]{m}$ , der Abstand zur rechten Wand $l_2 = \unit[10]{m}$ . 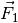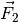Welche Beträge haben die Kräfte $\vec{F}_1$ und $\vec{F}_2$ , die entlang der Seilstücke auf diese einwirken?

SVG: Asymmetrische Kraftzerlegung am Beispiel einer Straßenlaterne
Lösung

Arten mechanischer Kräfte¶

Die folgenden Aufgaben beziehen sich auf den Abschnitt Arten mechanischer Kräfte.

(*) Welche Gewichtskraft entspricht einer Masse von $\unit[1]{kg}$ auf der Erde? Wie groß ist die Gewichtskraft der gleichen Masse auf dem Mond?

Lösung

(*) Die Gewichtskraft eines Astronauten beträgt auf dem Mond $\unit[130]{N}$ . Wie groß ist seine Gewichtskraft auf der Erde? Wie groß ist seine Masse?

Lösung

(*) Könnte man sich ohne Vorhandensein einer Reibungskraft überhaupt zu Fuß fortbewegen?

Lösung

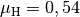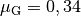(*) Eine $\unit[50]{kg}$ schwere Holzkiste aus Eichenholz soll auf einem Holzboden verschoben werden. Die Haftreibungszahl beträgt $\mu_{\mathrm{H}} = 0,54$ , die Gleitreibungszahl $\mu_{\mathrm{G}} = 0,34$ . Welche Kraft ist nötig, um die Kiste aus der Ruhelage in Bewegung zu versetzen, und welche Kraft ist nötig, um die Kiste weiter gleiten zu lassen?

Lösung

(*) Eine zu untersuchende Schraubenfeder dehnt sich durch das Einwirken einer Zugkraft $F = \unit[1,0]{N}$ um $\Delta s = \unit[33]{cm}$ . Wie groß ist die Federkonstante 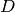$D$ der Schraubenfeder?

Lösung

(*) Welche Kraft ist nötig, um eine Schraubenfeder mit einer Federkonstante von $D=\unitfrac[40]{N}{m}$ um $\unit[12]{cm}$ auszudehnen?

Lösung

(*) Wie weit dehnt sich eine Schraubenfeder mit einer Federkonstante von $\unitfrac[650]{N}{m}$ , wenn man mit einer Kraft von $\unit[20]{N}$ an ihr zieht?

Lösung

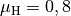(**) Welchen Radius $r$ muss ein Kreisverkehr mindestens haben, wenn ein Fahrzeug der Masse $m=\unit[1500]{kg}$ ihn mit einer Geschwindigkeit von $v = \unitfrac[36]{km}{h}$ ohne Wegrutschen durchfahren können soll? Als Haftreibungszahl kann dabei $\mu_{\mathrm{H}}= 0,8$ angenommen werden.

Lösung

Zurück zum Skript