Drehmoment und Gleichgewicht¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Drehmoment und Gleichgewicht.
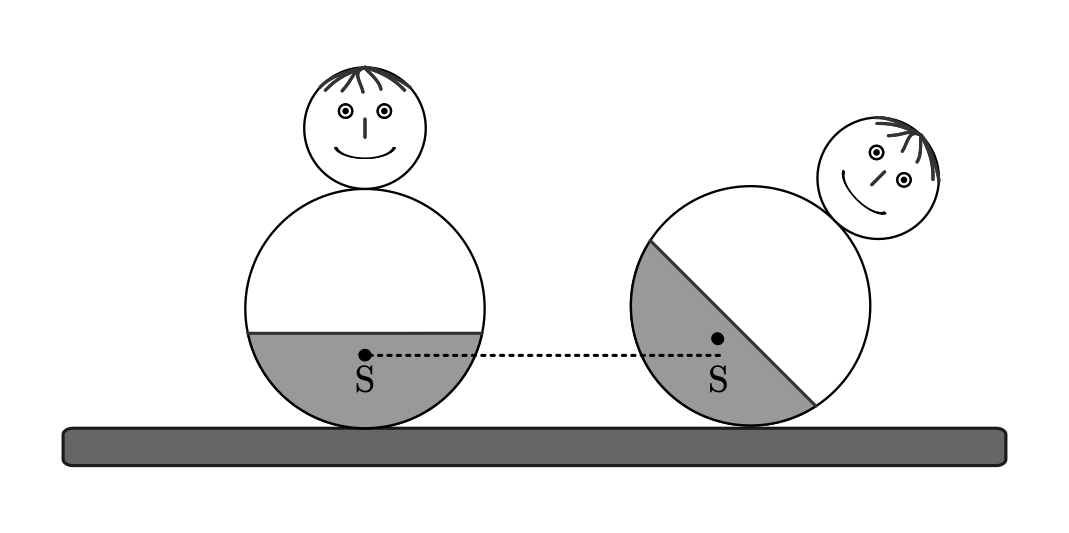
Die Standfestigkeit eines Körpers ist umso größer, je größer seine Masse und Standfläche und je tiefer sein Schwerpunkt ist.
Bei Stehaufmännchen muss der Schwerpunkt in der unteren Hälfte des Grundkörpers liegen; diese Verlagerung des Schwerpunkts wird durch einen Einbau von Zusatz-Gewichten im unteren Teil des Stehaufmännchens erreicht.
Wird ein Stehaufmännchen aus seiner aufrechten Position ausgelenkt, so wird dadurch der Schwerpunkt angehoben. Ein stabiles Gleichgewicht ist allerdings durch die niedrigst mögliche Lage des Schwerpunkts charakterisiert. Das Stehaufmännchen wird sich daher, wenn man es loslässt, von selbst wieder aufrichten, da hierdurch der Schwerpunkt zum niedrigsten Punkt zurückkehrt.
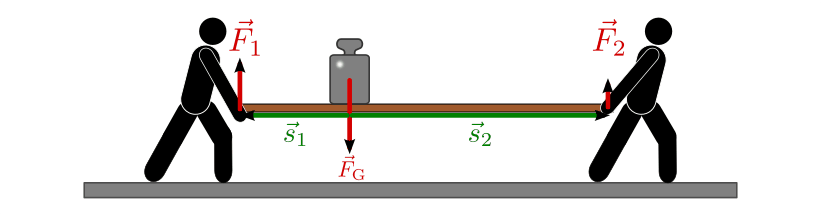
Während die Last getragen wird, ist sie im statischen Gleichgewicht; das heißt, die an ihr angreifenden Kräfte und Drehmomente ergeben in Summe jeweils Null. Betrachtet man zunächst nur den Einfluss
![F_{\mathrm{G}}=\unit[120]{N}](../_images/math/c65528a396a3d0199fa69dd634d4464731808663.png) der Last, so gilt:
der Last, so gilt: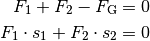
Die erste Gleichung ergibt sich daraus, dass die beiden von den Trägern ausgeübten Kräfte das Gewicht der Last ausgleichen, die Last also nicht nach unten sinkt. Die zweite Gleichung erhält man, wenn man sich jeweils einen der beiden Träger „weggeschnitten“ denkt; das Brett mitsamt Last würde dann kippen, wobei die Drehachse mit der Hand des verbliebenen Trägers identisch wäre. An der Stelle des jeweils „weggeschnittenen“ Trägers muss also eine Kraft wirken, die das von der Last bewirkte Drehmoment ausgleicht.
SVG: Gewichtsverteilung (Lösung)Aus der zweiten der obigen Gleichungen folgt:
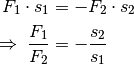
Die von den beiden Trägern aufzubringenden Kräfte stehen also im umgekehrten Verhältnis zu den jeweiligen Entfernungen der Last von den beiden Trägern. Das Vorzeichen ergibt sich daraus, dass die Wegstrecke
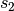 in die
umgekehrte Richtung zeigt wie
in die
umgekehrte Richtung zeigt wie 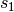 ; da linksdrehende Drehmomente
definitionsgemäß als positiv und rechtsdrehende Drehmomente definitionsgemäß
als positiv gezählt werden, erhält in diesem Fall
; da linksdrehende Drehmomente
definitionsgemäß als positiv und rechtsdrehende Drehmomente definitionsgemäß
als positiv gezählt werden, erhält in diesem Fall 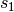 ein negatives
Vorzeichen. Mit
ein negatives
Vorzeichen. Mit ![s_1 = \unit[1]{m}](../_images/math/3b4d83206c74bb7d5d961e5b5d8ad2e7f7d34938.png) und
und ![s_2 = \unit[-2]{m}](../_images/math/a53c3fc68c202dd87601669aca8baf04c6b45113.png) folgt
also
folgt
also 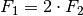 .
.Setzt man dieses Zwischenergebnis in die erste der obigen Gleichungen ein, so erhält man:
![F_1 + F_2 &= F_{\mathrm{G}} \\
(2 \cdot F_2) + F_2 &= F_{\mathrm{G}} \\
F_2 &= \frac{F_{\mathrm{G}}}{3} = \frac{\unit[120]{N}}{3} = \unit[40]{N}\\](../_images/math/7bb0f8c55e98601a31c6f0524b29ba62a3246113.png)
Der hintere Träger muss zum Heben der Last somit die Kraft
![F_1 =
\unit[80]{N}](../_images/math/d68750499bec78e48d19eb2d06f5fdf8e44c3dce.png) , der vordere Träger die Kraft
, der vordere Träger die Kraft ![F_2 = \unit[40]{N}](../_images/math/9f179a467e11ed47c16a538b63e28ffe96ae9029.png) aufbringen. Zusätzlich müssen beide Träger weitere
aufbringen. Zusätzlich müssen beide Träger weitere ![\unit[10]{N}](../_images/math/427f119ae47b073818745b78efd9146babe643e9.png) zum
Heben des Brettes aufbringen; dessen Gewicht verteilt sich nämlich (nach dem
gleichen Prinzip) gleichmäßig auf beide Träger, da sich sein Schwerpunkt in
der Mitte zwischen den beiden Personen befindet.
zum
Heben des Brettes aufbringen; dessen Gewicht verteilt sich nämlich (nach dem
gleichen Prinzip) gleichmäßig auf beide Träger, da sich sein Schwerpunkt in
der Mitte zwischen den beiden Personen befindet.