Arbeit, Leistung und Energie¶
Mechanische Arbeit¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanische Arbeit.
Beim Anheben einer Getränkekiste der Masse
![m = \unit[10]{kg}](../../_images/math/459ca4e8290a02336e78ce09a546ec08df11bb5a.png) um
um
![h = \unit[1]{m}](../../_images/math/21e9e7f07f46a475c2300dcf94c2c033ebbb1564.png) wird Hubarbeit verrichtet. Die Richtungen der
hebenden Kraft
wird Hubarbeit verrichtet. Die Richtungen der
hebenden Kraft 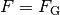 und Wegstrecke
und Wegstrecke 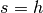 stimmen
überein, für den Betrag der verrichteten Arbeit
stimmen
überein, für den Betrag der verrichteten Arbeit 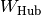 gilt somit:
gilt somit:![W_{\mathrm{Hub}} &= F \cdot s = F_{\mathrm{G}} \cdot h = m \cdot g \cdot h
\\[4pt]
&= \unit[10]{kg} \cdot \unit[9,81]{\frac{N}{kg} } \cdot \unit[1]{m} =
\unit[98,1]{N \cdot m} = \unit[98,1]{J}](../../_images/math/442264f4a912853bba296e693bc57e713c0cfd35.png)
Wird die Kiste
![\unit[1]{m}](../../_images/math/51a34f0de982f7a3c2dd6c9b85685eb17b0f71f0.png) über dem Boden gehalten, so muss zwar
die Gewichtskraft
über dem Boden gehalten, so muss zwar
die Gewichtskraft 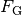 der Kiste ausgeglichen werden, doch
keine Arbeit verrichtet werden; die nötige Kraft wirkt dann nicht entlang
einer Wegstrecke – die Gewichtskraft der Kiste könnte beispielsweise auch
von einem Tisch „gehalten“ werden, ohne dass dieser Arbeit verrichtet bzw.
ihm Energie zugeführt werden muss.
der Kiste ausgeglichen werden, doch
keine Arbeit verrichtet werden; die nötige Kraft wirkt dann nicht entlang
einer Wegstrecke – die Gewichtskraft der Kiste könnte beispielsweise auch
von einem Tisch „gehalten“ werden, ohne dass dieser Arbeit verrichtet bzw.
ihm Energie zugeführt werden muss.Wird die Kiste in gleicher Höhe entlang einer beliebig langen Strecke getragen, so stehen die Richtungen der aufgewandten Kraft
 und der
zurück gelegten Wegstrecke
und der
zurück gelegten Wegstrecke  senkrecht aufeinander. Da somit keine
Kraft entlang des Weges
senkrecht aufeinander. Da somit keine
Kraft entlang des Weges  wirkt, wird beim Tragen der Kiste auf
gleicher Höhe auch keine Arbeit verrichtet.[1]
wirkt, wird beim Tragen der Kiste auf
gleicher Höhe auch keine Arbeit verrichtet.[1]
Beim Verschieben des Körpers wirkt die Zugkraft
![(F_{\mathrm{Zug}} =
\unit[25]{N})](../../_images/math/d8812ac963722c9db9c60ef169889972e3238723.png) entlang der zurückgelegten Wegstrecke
entlang der zurückgelegten Wegstrecke ![(s =
\unit[5]{m})](../../_images/math/5ae01a44619e8addeb1e3e393df5b018de500be0.png) . Für die verrichtete Arbeit
. Für die verrichtete Arbeit 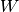 gilt damit:
gilt damit:![W = F_{\mathrm{Zug}} \cdot s = \unit[25]{N} \cdot \unit[5]{m} =
\unit[125]{J}](../../_images/math/e03a69877241d41f5f47734c647f4836d8b1e259.png)
Die Zugkraft verrichtet somit eine Arbeit von
![\unit[125]{J}](../../_images/math/b86389e842eb7ab03ede80369c8a942383571598.png) . Die
Schwerkraft
. Die
Schwerkraft ![F_{\mathrm{G}} = \unit[100]{N}](../../_images/math/630a32e5e9465727d485385de960ec39090eba1c.png) hingegen verrichtet keine
Arbeit, da sie senkrecht zur Wegstrecke
hingegen verrichtet keine
Arbeit, da sie senkrecht zur Wegstrecke  wirkt.[2]
wirkt.[2]
Um eine
![m = \unit[100]{kg}](../../_images/math/fa67b94803c61b73abdaaa02e944e916bb6dbde8.png) schwere Masse anzuheben, muss eine Kraft von
schwere Masse anzuheben, muss eine Kraft von
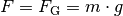 aufgebracht werden, wobei
aufgebracht werden, wobei ![g=
\unit[9,81 ]{N/kg}](../../_images/math/3734d30351809d9fe40a9e7023d966750428b559.png) den Ortsfaktor bezeichnet. Wird die Masse um
den Ortsfaktor bezeichnet. Wird die Masse um
![h=\unit[1]{m}](../../_images/math/d511ffcc4d07203d5258d904d801b85429c5deaa.png) angehoben, so ergibt sich mit der Formel der
Hubarbeit:
angehoben, so ergibt sich mit der Formel der
Hubarbeit:![W_{\mathrm{Hub}} &= F_{\mathrm{G}} \cdot h = m \cdot g \cdot h \\[4pt]
&= \unit[100]{kg} \cdot \unit[9,81]{\frac{N}{kg} } \cdot \unit[1]{m} =
\unit[981]{N \cdot m} = \unit[981]{J}](../../_images/math/4630501248b6cbdb0815158a0eca4549effdb8be.png)
Es ist somit eine Arbeit von
![\unit[981]{J}](../../_images/math/e2716d1ef1cfb7ee971af4434303eeb98db74ec6.png) (also knapp
(also knapp
![\unit[1]{kJ}](../../_images/math/91ddae21b26d08623d89ddac07cc02fa426104f7.png) ) nötig, um eine Masse von
) nötig, um eine Masse von ![\unit[100]{kg}](../../_images/math/be9452821f262a5e7d038160a6345abf15ebb36c.png) einen
Meter weit anzuheben.
einen
Meter weit anzuheben.
Um die Hubarbeit zu berechnen, die der Wanderer für seine eigene Masse
![(m_1 = \unit[70]{kg})](../../_images/math/5852e8e9e0d8487bd668ff3f42c58f959fcc95ca.png) und die Masse seines Rucksacks
und die Masse seines Rucksacks
![(m_2 = \unit[7]{kg})](../../_images/math/1ce8db80325985d1f92884129a0065837e50a4e6.png) beim Anstieg zum
beim Anstieg zum
![h=\unit[200]{m}](../../_images/math/ecc5209661fbe430ba1fb7537f027dfac4b20acf.png) höheren Gipfel aufzubringen hat, müssen die
gegebenen Werte nur in die Formel der Hubarbeit eingesetzt werden:
höheren Gipfel aufzubringen hat, müssen die
gegebenen Werte nur in die Formel der Hubarbeit eingesetzt werden:![W_1 &= m_1 \cdot g \cdot h = \unit[70]{kg} \cdot \unit[9,81]{\frac{N}{kg} }
\cdot \unit[200]{m} = \unit[137340]{N \cdot m} = \unit[137,34]{kJ} \\[4pt]
W_2 &= m_2 \cdot g \cdot h = \unit[7]{kg} \cdot \unit[9,81]{\frac{N}{kg} }
\cdot \unit[200]{m} = \unit[13734]{N \cdot m} = \unit[13,734]{kJ}](../../_images/math/1cea67255adaa1c910d359965c01f8c4e66610d2.png)
Insgesamt muss der Wanderer auf seinem Weg zum Gipfel somit eine Hubarbeit von
![W_{\mathrm{Hub}} = W_1 + W_2 \approx \unit[151]{kJ}](../../_images/math/f4af93c5e87dd72ee786dec48075f2955ac9f153.png) verrichten.[3]
verrichten.[3]
Ein Ziegelstein bildet das Fundament, die restlichen neun müssen je um ein entsprechendes Vielfaches der Ziegelsteinhöhe angehoben werden – der erste um
![h_1= \unit[7]{cm} = \unit[0,07]{m}](../../_images/math/52366292918f344cb99a8df9c59ae805faa483f9.png) , der zweite um
, der zweite um
![h_2 = \unit[14]{cm} = \unit[0,14]{m}](../../_images/math/6ec003047572a2f0b04dcd8adf8f0cc96ff65442.png) usw. Die Gesamtarbeit
entspricht der Summe aller einzelnen Hubarbeiten:
usw. Die Gesamtarbeit
entspricht der Summe aller einzelnen Hubarbeiten:![W_{\mathrm{Hub, gesamt}} &= F_{\mathrm{G}} \cdot h_1 + F_{\mathrm{G}}
\cdot h_2 + \ldots + F_{\mathrm{G}} \cdot h_{\mathrm{9}} \\
& = F_{\mathrm{G}} \cdot (h_1 + h_2 + \ldots + h_{\mathrm{9}})
\\
& = \unit[35]{N} \cdot (\unit[0,07]{m} + \unit[0,14]{m} + \ldots +
\unit[0,63]{m}) \\
& = \unit[35]{N} \cdot \unit[3,15]{m} \approx \unit[110,25]{J}](../../_images/math/3f3b66fa407b56467c27933aa5fa18ca7cb28570.png)
Die insgesamt zu verrichtende Arbeit beträgt somit
![\unit[110,25]{J}](../../_images/math/43034eb83d3ddcb8ed4d647ae173a7bda4c9fb48.png) .
.
Die verrichtete (Reibungs-)Arbeit lässt sich durch Einsetzen der gegebenen Werte
![F = \unit[15]{N}](../../_images/math/10de555af8270f2a0a79f0ab15d8215207c337d6.png) und
und ![s = \unit[5]{m}](../../_images/math/809fd08e0de324e4cdc4cee2a6570ed8c298220e.png) in die allgemeine
Definition der Arbeit berechnen:
in die allgemeine
Definition der Arbeit berechnen:![W = F \cdot s = \unit[15]{N} \cdot \unit[5]{m} = \unit[75]{N \cdot m} =
\unit[75]{J}](../../_images/math/13f02074cbb8dceec161e78f9b451ba9a629acde.png)
Es wird somit eine Arbeit von
![\unit[75]{J}](../../_images/math/c73a6a8072e3ffa874e6ea945cf7eb7bf50bd9a6.png) verrichtet.
verrichtet.
Die Gesamtmasse der Jugendlichen
![(m_1 = \unit[55]{kg} ,\, m2
= \unit[40]{kg})](../../_images/math/708ebaf145764aaabe7a87358b00f37bf44a7d55.png) und des Schlittens
und des Schlittens ![(m_{\mathrm{S}} = \unit[5]{kg})](../../_images/math/0b8f40d4c558cfa7374e2dff0b439eb367056655.png) ist gleich der Summe der einzelnen Massen:
ist gleich der Summe der einzelnen Massen:![m = m_1 + m_2 + m_{\mathrm{S}} = \unit[55]{kg} +
\unit[40]{kg} + \unit[5]{kg} = \unit[100]{kg}](../../_images/math/e73c9c8fa41cd7162bae3aa2f2457fed61bd238c.png)
Mit der (Gleit-)Reibungszahl
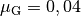 von Eisen auf Schnee
ergibt sich damit für die Reibungskraft
von Eisen auf Schnee
ergibt sich damit für die Reibungskraft 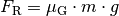 :
:![F_{\mathrm{R}} = \mu_{\mathrm{G}} \cdot m \cdot g = 0,04 \cdot \unit[100]{kg}
\cdot \unit[9,81]{\frac{N}{kg} } = \unit[39,24]{N}](../../_images/math/c02a5a958a47c53fe9f7ae0bcd3b6994efb2234a.png)
Diese Reibungskraft wird durch die Zugkraft
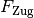 des
Pferdes ausgeglichen. Da die Kraft entlang der Strecke von
des
Pferdes ausgeglichen. Da die Kraft entlang der Strecke von ![s =
\unit[200]{m}](../../_images/math/46ac03e83f269bc877eae78706f2cee6667b3446.png) konstant ist, kann die Zugarbeit
konstant ist, kann die Zugarbeit 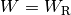 des
Pferdes ausgerechnet werden:
des
Pferdes ausgerechnet werden:![W = W_{\mathrm{R}} = F_{\mathrm{R}} \cdot s = \unit[39,24]{N} \cdot
\unit[250]{m} = \unit[7848]{N \cdot m} = \unit[7848]{J} \approx
\unit[7,5]{kJ}](../../_images/math/dc278a85239757c2215987afeb791badb925a057.png)
Das Pferd verrichtet beim Ziehen des Schlittens über das Feld somit eine Arbeit von rund
![\unit[7,5]{kJ}](../../_images/math/b9fdb6cbb0f795a9b429f092dee65a5e67ac7dc6.png) .
.
Für die zur Beschleunigung eines Körpers aus der Ruhelage
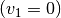 verrichtete Arbeit gilt:
verrichtete Arbeit gilt: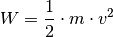
Setzt man die gegebenen Werte
![m = \unit[1000]{kg}](../../_images/math/dc7396c849afeb22ed84240bd5a9589f625ecaa1.png) und
und ![v = v
_2 = \unit[30]{m/s}](../../_images/math/8b69aad78fcb72d7f95b17474f4b07f6bfae5d0e.png) in die obige Gleichung ein, so ergibt sich:[4]
in die obige Gleichung ein, so ergibt sich:[4]![W &= \frac{1}{2} \cdot m \cdot v^2 = \frac{1}{2} \cdot \unit[1000]{kg}
\cdot (\unit[30]{\frac{m}{s} })^2 = \frac{1}{2} \cdot \unit[1000]{kg}
\cdot \unit[900]{\frac{m^2}{s^2} } \\ &= \unit[445\,000]{kg \cdot
\frac{m^2}{s^2} } = \unit[445\,000]{J}](../../_images/math/9932af4b8c3b32fa05f7f62a0348027e38f27e80.png)
Zur Beschleunigung des Fahrzeugs sind somit
![\unit[445\,000]{J}=
\unit[445]{kJ}](../../_images/math/86a7ee020c33ca8d0647cc45d001aba599ac1135.png) nötig.
nötig.
Um die Beschleunigungsarbeit zu berechnen, muss die Differenz zwischen Anfangs- und Endgeschwindigkeit
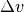 bekannt sein. Diese lässt
sich mittels der Werte der gegebenen Beschleunigung
bekannt sein. Diese lässt
sich mittels der Werte der gegebenen Beschleunigung ![a =
\unit[2,5]{m/s^2}](../../_images/math/dd1ad3120a6bd771b37972c405ef2da73a9d87ba.png) und ihrer Dauer
und ihrer Dauer ![\Delta t = \unit[10]{s}](../../_images/math/88bb26704c5cc588c9b6786c06969fbf156d4428.png) berechnen:
berechnen:![\Delta v = a \cdot \Delta t = \unit[2,5]{\frac{m}{s^2} } \cdot
\unit[10]{s} = \unit[25]{\frac{m}{s} }](../../_images/math/d7b7bad81463119c0ee396323a40f16d52ae3d84.png)
Daraus lässt sich mit
![m = \unit[750]{kg}](../../_images/math/7b826fb0171f17a79d5bb116224095fb6177c609.png) durch Einsetzen der Werte
in die Definition der Beschleunigungsarbeit die verrichtete Arbeit
durch Einsetzen der Werte
in die Definition der Beschleunigungsarbeit die verrichtete Arbeit
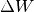 berechnen:
berechnen:![\Delta W &= \frac{1}{2} \cdot m \cdot (\Delta v)^2 = \frac{1}{2} \cdot
\unit[750]{kg} \cdot \left( \unit[25]{\frac{m}{s} }\right) ^2 =
\frac{1}{2} \cdot \unit[750]{kg} \cdot \unit[625]{\frac{m^2}{s^2} } \\ &=
\unit[234\,375]{kg \cdot \frac{m^2}{s^2} } = \unit[234\,375]{J}](../../_images/math/001d3623c218d9980c1dd1cb90f748f237ef61b7.png)
Die verrichtete Arbeit beträgt somit rund
![\unit[234]{kJ}](../../_images/math/dd3ecb2bf0bf24c515ea52fa163a94f3e09f0e18.png) .
.
Die zum Beschleunigen des Fahrzeugs auf
![v_1=\unit[50]{\frac{km}{h}}
\approx \unit[13,9]{\frac{m}{s}}](../../_images/math/f245e8bb2a1ccd9832c8c0ebd51c0c3ed8f2f1d1.png) nötige Arbeit beträgt mit
nötige Arbeit beträgt mit ![m =
\unit[1000]{kg}](../../_images/math/b35f221057221faa116bc835ac2615505b8b8cc4.png) :
:![W_{\mathrm{B,1}} = \frac{1}{2} \cdot m \cdot v_1^2 = \frac{1}{2} \cdot
\unit[1000]{kg} \cdot (\unit[13,9]{\frac{m}{s}})^2 \approx \unit[96\,451]{J}](../../_images/math/1c75aa320d11361239a5147056892bcb1ed61074.png)
Zum Beschleunigen des Fahrzeugs auf
![v_2=\unit[100]{\frac{km}{h}}
\approx \unit[27,8]{\frac{m}{s}}](../../_images/math/d2890e6b3a8c59efc49560d59c840679a83cf69b.png) muss folgende Arbeit verrichtet werden:
muss folgende Arbeit verrichtet werden:![W_{\mathrm{B,2}} = \frac{1}{2} \cdot m \cdot v_2^2 = \frac{1}{2} \cdot
\unit[1000]{kg} \cdot (\unit[27,8]{\frac{m}{s}})^2 \approx \unit[385\,802]{J}](../../_images/math/beaf4b09ca3a074cfc2eda57afa855566879165b.png)
Die zum Beschleunigen des Fahrzeugs von
![v_1=\unit[50]{\frac{km}{h}}](../../_images/math/f7de1eadda0203b15b9fad271a3ff8aa2e672dc1.png) auf
auf ![v_2 = \unit[100]{\frac{km}{h}}](../../_images/math/c7042d5fde62029d45b23011ad2cb51d41860b49.png) nötige Arbeitsmenge
nötige Arbeitsmenge
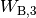 muss der Differenz
muss der Differenz  der
Arbeitsmengen entsprechen, die zum Beschleunigen aus der Ruhelage auf
der
Arbeitsmengen entsprechen, die zum Beschleunigen aus der Ruhelage auf
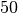 beziehungsweise
beziehungsweise ![\unit[100]{\frac{km}{h}}](../../_images/math/99ac0bd66194f23634d5b29aec3619b2733e99fc.png) nötig sind:
nötig sind:![W_{\mathrm{B,3}} = W_{\mathrm{B,2}} - W_{\mathrm{B,1}} =
\unit[385,802]{J} - \unit[96\,451]{J} \approx \unit[289\,351]{J}](../../_images/math/ebd1890d8d872ae65253a854131fd1b0a244b9f7.png)
Es sind somit rund
![\unit[289]{kJ}](../../_images/math/d91b8a11b1f5dca001fefa60e872bc14cc8c41f6.png) zum Beschleunigen von
zum Beschleunigen von 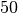 auf
auf
![\unit[100]{\frac{km}{h}}](../../_images/math/99ac0bd66194f23634d5b29aec3619b2733e99fc.png) an Beschleunigungsarbeit nötig.
an Beschleunigungsarbeit nötig.Hinweis: Die Arbeitsmenge
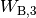 könnte ebenfalls mittels
könnte ebenfalls mittels
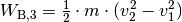 berechnet
werden; falsch wäre es hingegen,
berechnet
werden; falsch wäre es hingegen, 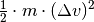 zu rechnen, da
zu rechnen, da 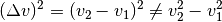 ist!
ist!
Wirkungsgrad¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Wirkungsgrad.
Nach der Goldenen Regel der Mechanik bleibt auch bei der Benutzung eines Flaschenzugs die zu verrichtende Arbeit
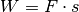 unverändert – zwar ist bei Benutzung eines
Flaschenzugs weniger Kraft nötig, dafür muss diese entlang einer
entsprechend längeren Wegstrecke aufgebracht werden. Die zugeführte Arbeit
unverändert – zwar ist bei Benutzung eines
Flaschenzugs weniger Kraft nötig, dafür muss diese entlang einer
entsprechend längeren Wegstrecke aufgebracht werden. Die zugeführte Arbeit
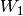 und die abgegebene Arbeit
und die abgegebene Arbeit 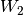 sind somit
gleich groß:
sind somit
gleich groß: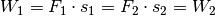
Damit gilt für den Wirkungsgrad
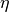 :
: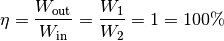
Der Wirkungsgrad eines idealen Flaschenzugs beträgt somit
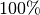 .
.
Die Menge an Hubarbeit
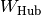 , die im Idealfall zum Heben der
Last (Gewichtskraft:
, die im Idealfall zum Heben der
Last (Gewichtskraft: ![F_{\mathrm{G}} = \unit[250]{N}](../../_images/math/5c623ded81f25c7250aa55fa029dfbecbab5841e.png) , Zughöhe:
, Zughöhe: ![h
= \unit[2]{m}](../../_images/math/9bb48245d6fb6ea7db11aa023f69c36744b3b380.png) ) nötig ist, lässt sich nach folgender Formel berechnen:
) nötig ist, lässt sich nach folgender Formel berechnen:![W_{\mathrm{Hub}} = F_{\mathrm{G}} \cdot h = \unit[250]{N} \cdot \unit[2]{m} =
\unit[500]{N \cdot m} = \unit[500]{J}](../../_images/math/e4d4186cea73ea4df3dfad6e9345361d21157ba0.png)
Diese Menge an Arbeit muss mit der Menge an Arbeit
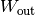 übereinstimmen, die vom Flaschenzug abgegeben wird. Es gilt somit
übereinstimmen, die vom Flaschenzug abgegeben wird. Es gilt somit
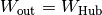 .
.Nach der Angabe reduziert sich durch die Verwendung des Flaschenzugs die aufzubringende Kraft auf
![\unit[80]{N}](../../_images/math/e418c017d84084f382b6295168edb89b5bbb383f.png) , die Zugstrecke beträgt dabei
, die Zugstrecke beträgt dabei
![s = \unit[7]{m}](../../_images/math/e88058a700de223e6e597c0f52be4549e23df0bc.png) . Somit wird folgende Arbeit am Flaschenzug
verrichtet:
. Somit wird folgende Arbeit am Flaschenzug
verrichtet:![W_{\mathrm{in}} = F \cdot s = \unit[80]{N} \cdot \unit[7]{m} = \unit[560]{N}](../../_images/math/9ccd1a6b73489128bce3e58afeb5a101c3939412.png)
Die vom Flaschenzug abgegebene Arbeit
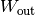 ist somit kleiner
als die investierte Arbeit
ist somit kleiner
als die investierte Arbeit 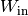 . Der Wirkungsgrad des
Flaschenzugs, der dem Verhältnis beider Größen entspricht, ist somit kleiner
als eins:
. Der Wirkungsgrad des
Flaschenzugs, der dem Verhältnis beider Größen entspricht, ist somit kleiner
als eins:![\eta = \frac{W_{\mathrm{out}}}{W_{\mathrm{in}}} =
\frac{\unit[500]{N}}{\unit[560]{N}} \approx 0,893](../../_images/math/4fd31d00b3bedd33b9bf79c116146435c2baf58d.png)
Der Wirkungsgrad
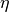 des Flaschenzugs beträgt also rund
des Flaschenzugs beträgt also rund
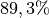 .
.
Um die Menge an abgegebener Arbeit
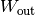 aus den
gegebenen Größen
aus den
gegebenen Größen ![W_{\mathrm{in}} = \unit[7200]{J}](../../_images/math/1b1bdd158ed2eeda3b7b602158603677c2462e7d.png) und
und 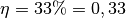 zu berechnen, muss man die Formel für den Wirkungsgrad
entsprechend umstellen:
zu berechnen, muss man die Formel für den Wirkungsgrad
entsprechend umstellen: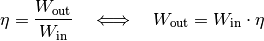
![W_{\mathrm{out}} = W_{\mathrm{in}} \cdot \eta = \unit[7200]{J} \cdot 0,33 =
\unit[2376]{J}](../../_images/math/2aec9936e82eb5102603049653fcbf988725d9cd.png)
Der Kraftwandler gibt somit
![\unit[2376]{W}](../../_images/math/92fcc8468b05ba3110675121f154075f18ba2395.png) an Arbeit ab.
an Arbeit ab.
Um die Menge an aufzuwendender Arbeit
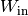 aus den
gegebenen Größen
aus den
gegebenen Größen ![W_{\mathrm{out}} = \unit[5000]{J}](../../_images/math/b02b0ac2988b0fd2ec76d74c5234906f82fe7aa6.png) und
und 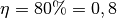 zu berechnen, muss die Formel für den Wirkungsgrad
umgestellt werden:
zu berechnen, muss die Formel für den Wirkungsgrad
umgestellt werden: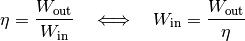
![W_{\mathrm{in}} = \frac{W_{\mathrm{out}}}{\eta } =
\frac{\unit[5000]{J}}{0,8} = \unit[6250]{J }](../../_images/math/55a3ae674b61ed1f06a71666aab2f3b8d4207274.png)
Es müssen somit
![\unit[6250]{J}](../../_images/math/a15e304ba7c82b47964f49d367d93d40e52f25cc.png) an Arbeit an der Vorrichtung
verrichtet werden.
an Arbeit an der Vorrichtung
verrichtet werden.
Mechanische Leistung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanische Leistung.
Die gesamte Arbeit
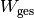 , die der Sportler verrichtet, lässt
sich als das Zehnfache der Hubarbeit
, die der Sportler verrichtet, lässt
sich als das Zehnfache der Hubarbeit 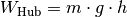 während eines Klimmzugs berechnen:[5]
während eines Klimmzugs berechnen:[5]![W_{\mathrm{ges}} &= 10 \cdot m \cdot g \cdot h \\
&= 10 \cdot \unit[70]{kg} \cdot \unit[9,81]{\frac{m}{s^2} } \cdot \unit[0,5]{m} \\
&= \unit[3433,5]{N \cdot m} = \unit[3433,5]{J}](../../_images/math/d0941d4179b6a52289cc4c8fdb42e241e2b65189.png)
Die Zeit, die der Sportler dafür benötigt, beträgt
![t = \unit[8]{s}](../../_images/math/11d18444407c611d8901f94d6a0b4c733b664b56.png) .
Damit beträgt seine Leistung
.
Damit beträgt seine Leistung 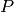 (Arbeit je Zeit):
(Arbeit je Zeit):![P = \frac{W_{\mathrm{ges}}}{t}
= \frac{\unit[3433,5]{J}}{\unit[8]{s}}
\approx \unit[429,2]{W}](../../_images/math/38ee5738feb64299e23ef4addc57ccf521aa6ce1.png)
Die Leistung des Sportlers beträgt somit rund
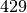 Watt.
Watt.
Die Leistung des Motors kann berechnet werden, indem man die bekannten Größen
![(m_{\mathrm{Last}} = \unit[200]{kg} ,\, h = \unit[4]{m} ,\, t =
\unit[6]{s})](../../_images/math/ccd7bf68fbdf5d6105e91524f479a65e69d09c13.png) in die Definition der Leistung einsetzt:
in die Definition der Leistung einsetzt:![P = \frac{W}{t} = \frac{m \cdot g \cdot h}{t} = \frac{\unit[200]{kg}
\cdot \unit[9,81]{\frac{N}{kg} } \cdot \unit[4]{m}}{\unit[6]{s}} =
\unit[1\,308]{\frac{N \cdot m}{s} } = \unit[1\,308]{W}](../../_images/math/92144e511b18b2ef9bec92cf79c8e440bf5bd3f2.png)
Die Leistung des Motors beträgt somit rund
![\unit[1,3]{kW}](../../_images/math/d2961de725a0d3f24b1169df9bb681423781ecad.png) .
.
Um die Masse
 zu bestimmen, die durch die Leistung
zu bestimmen, die durch die Leistung ![P =
\unit[1]{PS} = \unit[735]{W}](../../_images/math/3bb4fa37d8014cbba34b951c550c78c5302c0fd1.png) in
in ![t = \unit[1]{s}](../../_images/math/d486970377b90ea007f70b1a1706cac48396389f.png) um
um ![h =
\unit[1]{m}](../../_images/math/80ca9a6e3bfffd647f311e30550408b5d6dd52e2.png) angehoben werden kann, setzt man die Hubarbeit
angehoben werden kann, setzt man die Hubarbeit 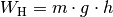 in die Definition der Leistung ein und löst
die Gleichung nach
in die Definition der Leistung ein und löst
die Gleichung nach  auf:
auf: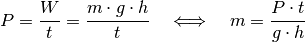
Mit
![\unit[1]{W} = \unit[1]{\frac{N \cdot m}{s} }](../../_images/math/b401f2b8c63381d102045a6d6a85a0915f1752ea.png) gilt:
gilt:![m = \frac{P \cdot t }{g \cdot h} = \frac{\unit[735]{\frac{N \cdot m}{s}
} \cdot \unit[1]{s}}{\unit[9,81]{\frac{N}{kg} } \cdot \unit[1]{m}}
\approx \unit[74,9]{kg}](../../_images/math/48336bcbc28b6f07cf2273abf3f431a6e1f3233c.png)
Mit einer Leistung von
![\unit[1]{PS} = \unit[735]{}](../../_images/math/2853e48219ebf4f8651317689527895791aebf46.png) kann somit eine
Masse von knapp
kann somit eine
Masse von knapp ![\unit[75]{kg}](../../_images/math/cdf23a38e3c9febdd3876471ec434911c76fb970.png) in einer Sekunde um einen Meter
angehoben werden.
in einer Sekunde um einen Meter
angehoben werden.
Ein Liter Wasser hat eine Masse von einem Kilogramm. Somit kann man die Wassermenge – wie bei der vorherigen Aufgabe – bestimmen, indem man die Hubarbeit
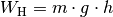 in die Definition der
Leistung einsetzt und die Gleichung nach
in die Definition der
Leistung einsetzt und die Gleichung nach  auflöst:
auflöst: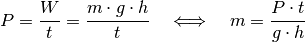
Mit
![\unit[1]{W} = \unit[1]{\frac{N \cdot m}{s} }](../../_images/math/b401f2b8c63381d102045a6d6a85a0915f1752ea.png) gilt mit
gilt mit ![P =
\unit[5]{kW} = \unit[5000]{W}](../../_images/math/62843b44cdb5c4af6c42f4fb355495007e19a65a.png) ,
, ![h = \unit[15]{m}](../../_images/math/6bd9a512015a5e936941122be10c36052f0feebe.png) und
und ![t =
\unit[1]{s}](../../_images/math/4b9983c7bc0d83f4653e0044d7a1d0012977296a.png) :
:![m = \frac{P \cdot t }{g \cdot h} = \frac{\unit[5000]{\frac{N \cdot m}{s}
} \cdot \unit[1]{s}}{\unit[9,81]{\frac{N}{kg} } \cdot \unit[15]{m}}
\approx \unit[34,0]{kg}](../../_images/math/96bf9e0ec14fbb911c1d0e915186af27a0b12dd2.png)
In einer Sekunde werden somit rund
![\unit[34]{kg} \equiv \unit[34]{l}](../../_images/math/c2eeecd5b1b8c2e94b17ba96cf9b2a966c1800de.png) Wasser nach oben gepumpt; bei gleicher Leistung beträgt die nach oben
gepumpte Wassermenge entsprend
Wasser nach oben gepumpt; bei gleicher Leistung beträgt die nach oben
gepumpte Wassermenge entsprend ![60 \cdot \unit[34]{l} \approx
\unit[2039]{l}](../../_images/math/96a56176c049e6a5960a46afad01de6c8d45c333.png) .
.
Für die mechanische Leistung
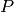 gilt allgemein:
gilt allgemein: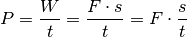
Mit
![v = \frac{s}{t} = \unit[0,75]{\frac{m}{s}}](../../_images/math/f84e34f6579776f24c213fe8e1686cd6433d1738.png) und
und ![F =
\unit[300]{N}](../../_images/math/dbecd3ed0997ab657f7a0794d0c65c8afca0d3a2.png) folgt somit für die mechanische Leistung beim Ziehen des
Schlittens:
folgt somit für die mechanische Leistung beim Ziehen des
Schlittens:![P = F \cdot \frac{s}{t} = \unit[300]{N} \cdot \unit[0,75]{\frac{m}{s}} =
\unit[225]{\frac{J}{s}} = \unit[225]{W}](../../_images/math/6def29955a4cfe09cd22388aca29f159d59c76d6.png)
Die mechanische Leistung beträgt somit
![\unit[225]{W}](../../_images/math/38f6475b0ff07211f313eeb79ab9d5354aeea73b.png) .
.
Die verrichtete Beschleunigungsarbeit beträgt mit
![m = \unit[1200]{kg}](../../_images/math/225b748d9f83fbb13a0d937db8a07d0946059e29.png) und
und ![v_2 = \unit[25]{m/s}](../../_images/math/33025b3923ac0212b43ab3bf05dde235ffa97582.png) und
und ![v_1 = \unit[15]{\frac{m}{s}}](../../_images/math/580443e681e32aa1e3b3bdbf9e4b80239eaa44f0.png) :
:![\Delta W &= \frac{1}{2} \cdot m \cdot (v_2^2 - v_1^2) = \frac{1}{2} \cdot
\unit[1200]{kg} \cdot \left( \left( \unit[25]{\frac{m}{s}} \right)^2 -
\left( \unit[15]{\frac{m}{s}} \right)^2 \right) \\ &= \frac{1}{2} \cdot
\unit[1200]{kg} \cdot \left( \unit[625]{\frac{m^2}{s^2} } -
\unit[225]{\frac{m^2}{s^2}} \right) = \unit[240\,000]{kg \cdot
\frac{m^2}{s^2} } = \unit[240\,000]{J}](../../_images/math/afb3b84d29f9d567d67dc40ab61d3189cf17907a.png)
Diese Arbeit wird in
![\Delta t = \unit[8]{s}](../../_images/math/75da2fea5fee14371bc801fe2b8b864bcee274b0.png) verrichtet. Damit lässt
sich auch die Beschleunigungs-Leistung
verrichtet. Damit lässt
sich auch die Beschleunigungs-Leistung 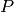 berechnen:
berechnen:![P = \frac{\Delta W}{\Delta t} = \frac{\unit[240\,000]{J}}{\unit[8]{s}}
\approx \unit[30\,000]{W}](../../_images/math/1b45f33d1c2f9020de8100d9a52018228f498c36.png)
Der Motor muss somit (abgesehen vom Luftwiderstand und von Reibungsverlusten im Getriebe) zur Beschleunigung mindestens
![\unit[30\,000]{W} =
\unit[30]{kW}](../../_images/math/0e0ae0709fce4beb4dba3ce72d0d405c4e0964c1.png) aufbringen.
aufbringen.
Mechanische Energie¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanische Energie.
Kann die Reibung vernachlässigt werden, so wird beim Herabfließen des Wassers dessen gesamte Höhenenergie
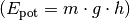 wieder
abgegeben. Bezogen auf
wieder
abgegeben. Bezogen auf ![\unit[1]{m^3} \equiv \unit[1000]{kg}](../../_images/math/e31c7a7a6718ce6f8fe8e5a5321511af533c35af.png) Wasser und
eine Fallhöhe von
Wasser und
eine Fallhöhe von ![h = \unit[110]{m}](../../_images/math/daf243a38581c8842c82ff9a0c1aa624c0e9fdde.png) ergibt sich:
ergibt sich:![E_{\mathrm{pot}} &= m \cdot g \cdot h
= \unit[1000]{kg} \cdot \unit[9,81]{\frac{m}{s^2} } \cdot
\unit[110]{m}
= \unit[1\,079\,100]{N \cdot m } = \unit[1\,079\,100]{J} =
\unit[1\,079,1]{kJ}](../../_images/math/7ace7fa76a1ee129bffdb51cf6ddefb922dd281b.png)
Diese Energiemenge entspricht übrigens dem Energiegehalt von etwa
![\unit[100]{g}](../../_images/math/b25c7db38f69092eb13d4bb9ac59285044dfbd1c.png) Brot (
Brot (![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) Brot enthält rund
Brot enthält rund
![\unit[10\,500]{kJ}](../../_images/math/56b66c982866077ad126784879c90978b704938b.png) an chemischer Energie).
an chemischer Energie).
Die Formel für die Bewegungsenergie lautet
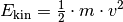 . Setzt man in diese Gleichung die Massen
. Setzt man in diese Gleichung die Massen ![m
_{\mathrm{PKW}} = \unit[1\,000]{kg}](../../_images/math/f3022f8fb680e783107481b69ed744575c67a592.png) und
und ![m_{\mathrm{LKW}} = \unit[8\,000]{kg}](../../_images/math/51b96ec88ac893a79d9d453c94249ef7c93e4bdf.png) der beiden Fahrzeuge sowie ihre Geschwindigkeit
der beiden Fahrzeuge sowie ihre Geschwindigkeit ![v_1 =
\unit[50]{\frac{km}{h} } \approx \unit[13,89]{\frac{m}{s} }](../../_images/math/cd7a5acc87a0c31ba7f6d59fd94427d99d311583.png) ein, so erhält
man:
ein, so erhält
man:![E_{\mathrm{kin, PKW,1}} = \frac{1}{2} \cdot m_{\mathrm{PKW}} \cdot v_1^2 &=
\frac{1}{2} \cdot \unit[1\,000]{kg} \cdot \left(
\unit[13,89]{\frac{m}{s} } \right) ^2 \\ &= \unit[96\,466]{kg \cdot
\frac{m^2}{s^2} } = \unit[96\,466]{J} \approx \unit[96,5]{kJ} \\
E_{\mathrm{kin, LKW}} = \frac{1}{2} \cdot m_{\mathrm{LKW}} \cdot v_1^2 &=
\frac{1}{2} \cdot \unit[8\,000]{kg} \cdot \left(
\unit[13,89]{\frac{m}{s} } \right) ^2 \\ &= \unit[771\,728,4]{kg \cdot
\frac{m^2}{s^2} } = \unit[771\,728,4]{J} \approx \unit[771,7]{kJ} \\](../../_images/math/ffbbd61ec1e4877a25dbc14f797dab2e71975cc1.png)
Durch seine achtfache Masse besitzt der LKW bei gleicher Geschwindigkeit gegenüber dem PKW auch eine achtfache Energie. Wird der PKW auf
![v
_2 = \unit[100]{\frac{km}{h} } \approx \unit[27,78]{\frac{m}{s} }](../../_images/math/0445307e25612996bda38e5bf5cee74dcb38dcd4.png) beschleunigt, so beträgt seine Energie:
beschleunigt, so beträgt seine Energie:![E_{\mathrm{kin, PKW,2}} = \frac{1}{2} \cdot m_{\mathrm{PKW}} \cdot v_2^2 &=
\frac{1}{2} \cdot \unit[1\,000]{kg} \cdot \left(
\unit[27,78]{\frac{m}{s} } \right)^2 \\ &= \unit[385\,864,2]{kg \cdot
\frac{m^2}{s^2} } = \unit[385\,864,2]{J} \approx \unit[385,9]{kJ}](../../_images/math/fa7a685818a809964c0b62f245c7110fef66aebd.png)
Durch den quadratischen Zusammenhang zwischen Geschwindigkeit und Bewegungsenergie hat der PKW bei einer doppelten Geschwindigkeit eine vierfache Bewegungsenergie. Bei einer dreifachen Geschwindigkeit
![v=
\unit[150]{\frac{km}{h} } = \unit[41,67]{\frac{m}{s} }](../../_images/math/287549764dc0197caa9623ef9683b16d0121429e.png) nimmt die
Bewegungsenergie des PKWs entsprechend auf das neun-fache zu:
nimmt die
Bewegungsenergie des PKWs entsprechend auf das neun-fache zu:![E_{\mathrm{kin, PKW,3}} = \frac{1}{2} \cdot m_{\mathrm{PKW}} \cdot v_2^2 &=
\frac{1}{2} \cdot \unit[1\,000]{kg} \cdot \left(
\unit[41,67]{\frac{m}{s} } \right) ^2 \\ &= \unit[868\,194,5]{kg \cdot
\frac{m^2}{s^2} } = \unit[868\,194,5]{J} \approx \unit[868,2]{kJ}](../../_images/math/f481f5b0bd111be78d171e37552570bab137203b.png)
Somit besitzt der PKW bei einer dreifachen Geschwindigkeit eine höhere Bewegungsenergie als der achtmal schwerere LKW.
Um die Höhe zu bestimmen, deren Energie einer Bewegung mit
![\unit[72]{\frac{km}{h} } = \unit[20]{\frac{m}{s} }](../../_images/math/d2032855e73bdc84f8ab8781b817f712b2cbed6a.png) entspricht, setzt
man die Formeln für die Höhenenergie
entspricht, setzt
man die Formeln für die Höhenenergie 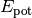 und die
Bewegungsenergie
und die
Bewegungsenergie 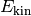 gleich:
gleich: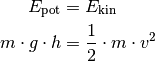
Beide Größen sind direkt proportional zur Geschwindigkeit. In der obigen Gleichung kann die Masse
 somit auf beiden Seiten „gekürzt“
werden. Anschließend kann die Gleichung nach der gesuchten Höhe
somit auf beiden Seiten „gekürzt“
werden. Anschließend kann die Gleichung nach der gesuchten Höhe 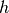 aufgelöst und der Wert
aufgelöst und der Wert ![v = \unit[20]{\frac{m}{s} }](../../_images/math/5831f0e56d7c240b79c9f5802738b84af925859e.png) für die
Geschwindigkeit eingesetzt werden:
für die
Geschwindigkeit eingesetzt werden:![h &= \frac{\frac{1}{2} \cdot v^2}{g} = \frac{v^2}{2 \cdot g} \\
&= \frac{\left( \unit[20]{\frac{m}{s}} \right)^2 }{2 \cdot
\unit[9,81]{\frac{m}{s^2} }} = \frac{\unit[400]{\frac{m^2}{s^2} }}{2
\cdot \unit[9,81]{\frac{m}{s^2} }} \approx \unit[20,39]{m}](../../_images/math/879bd6a4dcd9d3c8c4c2d712517a615ed73734ae.png)
Ein Aufprall eines Fahrzeugs mit
![\unit[70]{\frac{km}{h}}](../../_images/math/73d8dcb0338820c854a84ccd6a8ad04d489d9269.png) entspricht
somit einem ungebremsten Sturz aus etwa
entspricht
somit einem ungebremsten Sturz aus etwa ![\unit[20]{m}](../../_images/math/5141fe92c0d3e4ee12ff8532650e0738b81dd443.png) Höhe.
Höhe.
Um die Geschwindigkeit des Badegasts beim Eintauchen zu ermitteln, kann die Höhenenergie
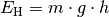 auf dem Sprungbrett
auf dem Sprungbrett
![(h=\unit[5]{m})](../../_images/math/57ca033dd41b345bae26c991a2cd15bb0bd9f21a.png) mit der kinetischen Energie
mit der kinetischen Energie 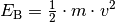 unmittelbar vor dem Eintauchen gleichgesetzt
werden:
unmittelbar vor dem Eintauchen gleichgesetzt
werden: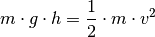
Auf beiden Seiten der Gleichung kann die Masse
 gekuerzt werden.
Nach dem Aufloesen der Gleichung ergibt sich fuer die Geschwindigkeit
gekuerzt werden.
Nach dem Aufloesen der Gleichung ergibt sich fuer die Geschwindigkeit
 :
:![g \cdot h &= \frac{1}{2} \cdot v^2 \\
\Rightarrow v &= \sqrt{2 \cdot g \cdot h} \\ &= \sqrt{ 2 \cdot
\unit[9,81]{\frac{m}{s^2}} \cdot \unit[5]{m}} =
\sqrt{\unit[98,1]{\frac{m^2}{s^2}}} \approx \unit[9,9]{\frac{m}{s}}](../../_images/math/0870f1b9871e982c3b62b937598983be9f715ff5.png)
Die Geschwindigkeit des Badegasts beim Eintauchen betraegt somit rund
![\unit[9,9]{\frac{m}{s}}](../../_images/math/923e9dbba0e563d770988ea17e366fea155798fd.png) , also etwa
, also etwa ![\unit[35,6]{\frac{km}{h}}](../../_images/math/64710e1d3ce0686387d4538d1ab89e58f3390b49.png) .
.
Ja, alle Nahrungsmittel enthalten indirekt Sonnenlicht. Pflanzen wandeln diese mittels der Photosynthese zunächst in Zucker, anschließend (auch) in längerkettige Kohlenhydrate (Stärke, Zellulose) um. Über ein ganzes Jahr gesehen, haben Nahrungsmittel-Pflanzen dabei einen Wirkungsgrad von etwa
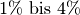 . Gründe hierfür sind Nacht-Zeiten, in denen der
Stoffwechsel der Pflanzen umgekehrt abläuft, wechselnde Beleuchtung,
Abschattungsverluste durch Überlagerung von Blättern, keine maximale
Kohlenstoffdioxid-Konzentration usw.
. Gründe hierfür sind Nacht-Zeiten, in denen der
Stoffwechsel der Pflanzen umgekehrt abläuft, wechselnde Beleuchtung,
Abschattungsverluste durch Überlagerung von Blättern, keine maximale
Kohlenstoffdioxid-Konzentration usw.Tiere leben ihrerseits – direkt oder indirekt – von Pflanzen. Da der „Wirkungsgrad“ der Nahrungsaufnahme stets kleiner als Eins ist und die Tiere selbst Energie zum Aufrechthalten der Körpertemperatur sowie für Bewegung, Stoffwechsel usw. brauchen, ist es nicht verwunderlich, dass bei Verwendung tierischer Produkte stets die rund
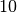 -fache Menge an pflanzlichen
Futtermitteln benötigt wird. Entsprechend geringer ist der „Wirkungsgrad“
tierischer Produkte, er liegt stets in der Größenordnung von nur
-fache Menge an pflanzlichen
Futtermitteln benötigt wird. Entsprechend geringer ist der „Wirkungsgrad“
tierischer Produkte, er liegt stets in der Größenordnung von nur
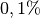 .
.
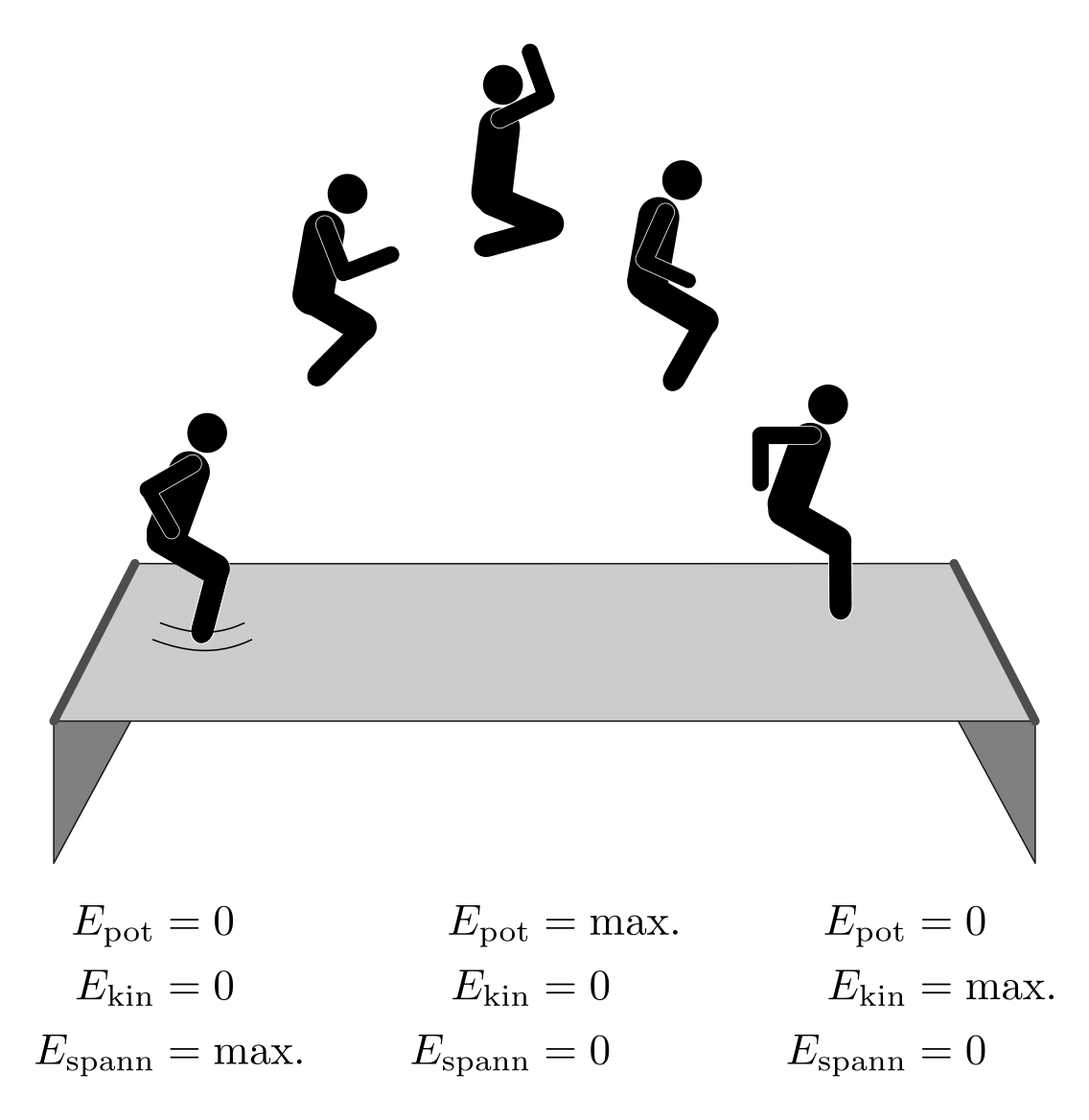
In der Ausgangsposition besitzt der Körper des Trampolinspringers weder Bewegungsenergie
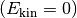 noch Höhenenergie
noch Höhenenergie 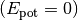 ; dafür ist das elastische Trampolintuch maximal gespannt.
Diese Spannenergie
; dafür ist das elastische Trampolintuch maximal gespannt.
Diese Spannenergie 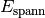 bewirkt dann eine Beschleunigung
bzw. ein Anheben des Körpers.
bewirkt dann eine Beschleunigung
bzw. ein Anheben des Körpers.SVG: Energieerhaltung beim Trampolinspringen (Lösung)Am höchsten Punkt wurde die gesamte Bewegungsenergie in Höhenenergie umgewandelt. Anschließend findet in umgekehrter Weise eine Umwandlung von Höhenenergie in Bewegungsenergie statt; unmittelbar vor dem erneuten Kontakt mit dem Trampolintuch ist die Geschwindigkeit des Springers und damit seine kinetische Energie maximal.
Anmerkungen:
| [1] | Man könnte die Kiste ebenso auf einem Rollenwagen entlang der ebenen
Strecke  transportieren und dabei lediglich die anfallende Reibung
(Rollreibung und Luftwiderstand) überwinden – diese versucht man bei
Transportprozessen durch geschickte Bauformen, reibungsarme Kugellager usw.
zu minimieren. transportieren und dabei lediglich die anfallende Reibung
(Rollreibung und Luftwiderstand) überwinden – diese versucht man bei
Transportprozessen durch geschickte Bauformen, reibungsarme Kugellager usw.
zu minimieren. |
| [2] | Die Gewichtskraft kann lediglich als Ursache der Reibungskraft angesehen
werden, gegen die beim Verschieben der Kiste Arbeit verrichtet wird. Aus der
Formel für die Reibungskraft 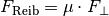 folgt dabei für den Reibungskoeffizienten folgt dabei für den Reibungskoeffizienten ![\mu =
\frac{F_{\mathrm{Reib}}}{F_{\mathrm{\perp}}} =
\frac{F_{\mathrm{Zug}}}{F_{\mathrm{G}}} = \frac{\unit[25]{N}}{\unit[100]{N}}
= 0,25](../../_images/math/59b7b5eb045d3194ed033b65c6a2bfa0a9e3bb33.png) . . |
| [3] | Alternativ kann man zur Lösung der Aufgabe auch zuerst die Massen
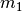 und und 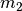 zu einer Gesamtmasse zu einer Gesamtmasse 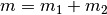 addieren und diese in die Formel der Hubarbeit einsetzen.
addieren und diese in die Formel der Hubarbeit einsetzen. |
| [4] | Nach der Definition
Für die Einheit der Arbeit gilt somit:
|
| [5] | Bei der Bestimmung der Einheit wurde einerseits berücksichtigt, dass
![\unit[1]{N} = \unit[1]{kg \cdot \frac{m}{s^2} }](../../_images/math/51c17f1910bb038d4cd9b177928bee952f74a6c7.png) gilt (dies folgt aus
dem Newtonschen Kraftgesetz); andererseits gilt
nach der Definition der Energie-Einheit gilt (dies folgt aus
dem Newtonschen Kraftgesetz); andererseits gilt
nach der Definition der Energie-Einheit ![\unit[1]{J} = \unit[1]{N
\cdot m}](../../_images/math/75b7a165aad64315362f687545e53311cc0f6b53.png) . . |

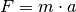 gilt für die Einheit
der Kraft:
gilt für die Einheit
der Kraft:![\unit[1]{N} = \unit[1]{kg \cdot \frac{m}{s^2}}{\color{white} \qquad
\quad \;\; \ldots}](../../_images/math/856aa33c772112549d9615d7fe72ee7014c60320.png)
![\unit[1]{J} = \unit[1]{N \cdot m} = \unit[1]{kg \cdot \frac{m^2}{s^2} }](../../_images/math/37a7d16e3864e5a46170d8fb5464e2db047c1924.png)