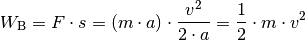Mechanische Arbeit¶
Wirkt eine Kraft auf einen Körper ein und bewirkt dabei eine Verformung, eine Beschleunigung oder ein Anheben des Körpers, so wird physikalische Arbeit verrichtet. Um die Größe der verrichteten Arbeit zu bestimmen, müssen der Betrag der Kraft und die Länge des Weges, entlang dessen die Kraft wirkt, bekannt sein.
Definition:
Die Arbeitist das Produkt aus der in Richtung des Weges wirkenden Kraft
und der zurückgelegten Wegstrecke
:[1]
(1)¶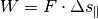
Einheit:
Die Einheit der Arbeit ist nach Gleichung (1) das Produkt der Einheiten von Kraft und Weg. Sie wird nach James Prescott Joule kurzerhand Joulegenannt.
![\unit[1]{J} = \unit[1]{N } \cdot \unit[1]{m}](../../_images/math/74d8da3d8b663a42d694dfcde2c465d26c70c5e9.png)
Beispiele:
- Die Gewichtskraft
 einer Tafel Schokolade
einer Tafel Schokolade ![( m =
\unit[100]{g})](../../_images/math/6d118c00bbd07a790965b0cdcbf12352d429020d.png) entspricht in guter Näherung
entspricht in guter Näherung ![\unit[1]{N}](../../_images/math/d4bc2af6cd73b1a3c5f1086f5f01daf958c78dac.png) . Hebt man
eine Tafel Schokolade einen Meter weit an (egal von welcher Position aus), so
verrichtet man dabei eine Arbeit von
. Hebt man
eine Tafel Schokolade einen Meter weit an (egal von welcher Position aus), so
verrichtet man dabei eine Arbeit von ![W = F_{\mathrm{G}} \cdot s =
\unit[1]{N} \cdot \unit[1]{m} = \unit[1]{J}](../../_images/math/5ace07fe69c4230cf1cb4d258af32d6eddf7f513.png) .
. - Hebt man
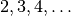 Tafeln Schokolade einen Meter weit an, so
verrichtet man entsprechend eine Arbeit von
Tafeln Schokolade einen Meter weit an, so
verrichtet man entsprechend eine Arbeit von ![\unit[2, 3, 4, \ldots]{J}](../../_images/math/9ba238129d4899d217c0d7916634b4eb3f9b5bc9.png) .
Mit der gleichen Arbeit könnte man jeweils auch eine Tafel Schokolade um
.
Mit der gleichen Arbeit könnte man jeweils auch eine Tafel Schokolade um
![\unit[2, 3, 4, \ldots]{m}](../../_images/math/be7a1f39a0df3dde23d1b65b13335ef08caab982.png) anheben.
anheben. - Um zwei Tafeln Schokolade zwei Meter weit anzuheben, muss man eine Arbeit von
![\unit[2]{N} \cdot \unit[2]{m} = \unit[4]{N \cdot m} = \unit[4]{J}](../../_images/math/96a93b8bf76db86456b9f46f9d902fa4e3b858ce.png) verrichten.
verrichten.
Unter der Bedingung, dass die Kraft konstant ist und in beliebiger, aber fester Richtung wirkt, gilt:
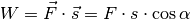
Hierbei bezeichnet  den Winkel zwischen der wirkenden Kraft und
der zurückgelegten Wegstrecke.
den Winkel zwischen der wirkenden Kraft und
der zurückgelegten Wegstrecke.
Arten mechanischer Arbeit¶
Bei mechanischen Prozessen sind die folgenden Arten mechanischer Arbeit von entscheidender Bedeutung:
Hubarbeit
Erfahrungsgemäß ist es einfacher, einen leichten Körper hoch zu heben als einen schweren. Doch auch beim Heben zweier gleich schwerer Körper gibt es Unterschiede: Je weiter man einen Körper hoch heben muss, desto mehr Arbeit ist dafür nötig.
Definition:
(2)¶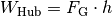
Die Hubarbeit kann mit Hilfe der Formel für die Gewichtskraft
(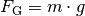 ) auch als
) auch als 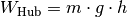 geschrieben werden.
geschrieben werden.
Reibungsarbeit
Um einen Körper auf einer waagrechten Ebene gleichförmig zu bewegen, muss der Reibungskraft eine gleich große Gegenkraft entgegenwirken.
Definition:
(3)¶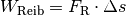
Beim gleichzeitigen Auftreten mehrerer Reibungskräfte (beispielsweise
Rollreibung und Luftwiderstand) entspricht 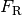 der Summe
aller auftretenden Reibungskräfte.
der Summe
aller auftretenden Reibungskräfte.
Spannarbeit
Die Spannkraft, die ein elastischer Körper (beispielsweise eine Schraubenfeder) einer Stauchung oder Streckung entgegensetzt, ist nicht konstant, sondern nimmt gleichmäßig mit der Auslenkung zu:
- Die anfängliche Spannkraft der Feder in der Ruhelage ist Null.
- Wird die Feder um eine Wegstrecke
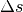 ausgelenkt, so beträgt die
Spannkraft der Feder
ausgelenkt, so beträgt die
Spannkraft der Feder 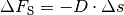 .
.
Entlang der Strecke 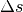 muss im Durchschnitt nur die Hälfte der
(maximalen) Spannkraft
muss im Durchschnitt nur die Hälfte der
(maximalen) Spannkraft 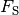 am Auslenkungspunkt aufgewendet
werden. Für die durchschnittlich nötige Kraft
am Auslenkungspunkt aufgewendet
werden. Für die durchschnittlich nötige Kraft 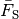 gilt
also:
gilt
also:
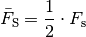
Dies gilt allgemein für elastische Verformungen.
Definition:
Die zur Verformung eines elastischen Körpers (beispielsweise einer Schraubenfeder) nötige Spannarbeitist proportional zur durchschnittlichen Spannkraft
und der dazugehörigen Auslenkung
:
(4)¶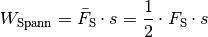
Die Spannarbeit kann mit Hilfe der Formel für die Spannkraft
(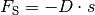 ) auch als
) auch als 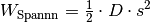 geschrieben werden, wobei
geschrieben werden, wobei 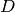 die (oftmals
experimentell zu bestimmende) Federkonstante des Körpers angibt.
die (oftmals
experimentell zu bestimmende) Federkonstante des Körpers angibt.
Beschleunigungsarbeit
Zur Überwindung der Trägheit ist eine Kraft notwendig. Die zugehörige Arbeit,
die bei einer Beschleunigung entlang einer Strecke  auftritt, heißt
Beschleunigungsarbeit.
auftritt, heißt
Beschleunigungsarbeit.
Definition:
Die Beschleunigungsarbeiteines zunächst ruhenden Körpers der Masse
ist proportional zum Quadrat der Endgeschwindigkeit
, die dieser erreicht:[2]
(5)¶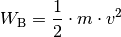
Besitzt der Körper bereits eine Anfangsgeschwindigkeit 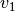 und wird auf
eine Endgeschwindigkeit
und wird auf
eine Endgeschwindigkeit 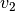 beschleunigt, so beträgt die
Beschleunigungsarbeit
beschleunigt, so beträgt die
Beschleunigungsarbeit 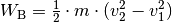 .
.
Rotationsarbeit
Zur Überwindung der Trägheit ist für eine Rotation ein Drehmoment notwendig. Die zugehörige Arbeit heißt Rotationsarbeit.
Definition:
Die Rotationsarbeiteines zunächst ruhenden Körpers mit Trägheitsmoment
ist proportional zum Quadrat der Winkelgeschwindigkeit
, die dieser erreicht:
(6)¶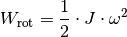
Besitzt der Körper bereits eine Anfangsgeschwindigkeit 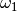 und wird auf eine Endgeschwindigkeit
und wird auf eine Endgeschwindigkeit 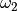 beschleunigt, so
muss in Gleichung (6) anstelle
beschleunigt, so
muss in Gleichung (6) anstelle  die
Differenz
die
Differenz 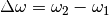 beider
Winkelgeschwindigkeiten eingesetzt werden.
beider
Winkelgeschwindigkeiten eingesetzt werden.
Goldene Regel der Mechanik¶
Während Kräfte durch entsprechende Hilfsmittel in ihrer Richtung oder ihrem Betrag geändert werden können, kann die für einen mechanischen Prozess nötige Arbeit nicht verringert werden; die Menge an Arbeit bleibt erhalten.
Bei Verwendung eines Kraftwandlers ist die aufgenommene Arbeit stets gleich der abgegebenen Arbeit (Reibung wird vernachlässigt):
![F_1 \cdot \Delta s_1 &= F_2 \cdot \Delta s_2 \\[6pt]
W_1 &= W_2](../../_images/math/6e1e800f2f924088b5a97837f00e504949f92a4a.png)
Abgesehen von Reibungsverlusten bleibt das Produkt aus Weg und Kraft (entlang des Weges) stets konstant. Eine umgangssprachliche Formulierung für das Prinzip der Kraftwandlung („die goldene Regel der Mechanik“) lautet daher:
„Was an Kraft eingespart wird, muss an Weg zugesetzt werden.“
Beispiele:
Bei einer festen Rolle ist die zum Heben aufgewendete Kraft
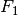 gleich der wirksamen Kraft
gleich der wirksamen Kraft 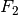 . Der Weg der Kraft
. Der Weg der Kraft
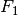 ist gleich dem Weg der Kraft
ist gleich dem Weg der Kraft 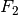 . Somit gilt:
. Somit gilt: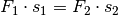
Bei einer losen Rolle ist die zum Heben aufgewendete Kraft
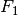 gleich der Hälfte der wirksamen Kraft
gleich der Hälfte der wirksamen Kraft 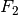 . Der Weg der
Kraft
. Der Weg der
Kraft 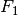 ist allerdings doppelt so groß wie der Weg der Kraft
ist allerdings doppelt so groß wie der Weg der Kraft
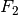 . Insgesamt gilt:
. Insgesamt gilt: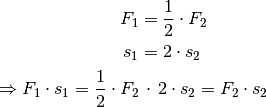
Um einen Körper mit einer Gewichtskraft
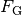 auf eine Höhe
auf eine Höhe
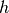 zu heben, ist die Hubarbeit
zu heben, ist die Hubarbeit 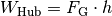 nötig. Verschiebt man ihn hingegen entlang des längeren Weges
nötig. Verschiebt man ihn hingegen entlang des längeren Weges  einer schiefen Ebene nach oben, so ist die nötige
Kraft
einer schiefen Ebene nach oben, so ist die nötige
Kraft  um das Verhältnis
um das Verhältnis 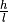 geringer. Es gilt:
geringer. Es gilt: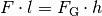
Anmerkungen:
| [1] | Die Arbeits-Formel
Im Fall einer sich kontinuierlich ändernden Kraft wird aus der Summe
|
| [2] | Um die Formel für die Beschleunigungsarbeit
|
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

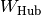 ist proportional zur
ist proportional zur
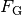 eines
angehobenen Körpers und zur Hubhöhe
eines
angehobenen Körpers und zur Hubhöhe 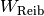 ist proportional zur
ist proportional zur
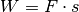 gilt streng genommen nur, wenn
die wirkende Kraft F konstant ist. Ist die Kraft nur innerhalb einzelner
Zeitabschnitte konstant, so muss man die Formel für jeden dieser
Zeitabschnitte einzeln anwenden und die jeweiligen Teilbeträge summieren.
gilt streng genommen nur, wenn
die wirkende Kraft F konstant ist. Ist die Kraft nur innerhalb einzelner
Zeitabschnitte konstant, so muss man die Formel für jeden dieser
Zeitabschnitte einzeln anwenden und die jeweiligen Teilbeträge summieren.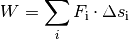
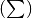 ein Integral
ein Integral 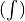 .
.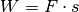 aus. Für die Kraft
aus. Für die Kraft 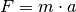 einsetzen. Für die Wegstrecke kann man die
einsetzen. Für die Wegstrecke kann man die
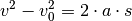 nach
nach
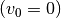 , so ist
, so ist 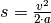 . Setzt man
auch diesen Ausdruck in die allgemeine Definition der Arbeit ein, so erhält
man:
. Setzt man
auch diesen Ausdruck in die allgemeine Definition der Arbeit ein, so erhält
man: