Arbeit, Leistung und Energie¶
Mechanische Arbeit¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Mechanische Arbeit.
(*) Warum handelt es sich um Arbeit, wenn man eine
![\unit[10]{kg}](../../_images/math/2b92a4a959a6eb04e87a3543c0908035fb15ad48.png) schwere Getränke-Kiste um
schwere Getränke-Kiste um ![\unit[1]{m}](../../_images/math/51a34f0de982f7a3c2dd6c9b85685eb17b0f71f0.png) anhebt? Verrichtet man auch
Arbeit, wenn man die Kiste längere Zeit in dieser Höhe hält? Handelt es sich
um Arbeit, wenn die Kiste auf gleicher Höhe entlang einer
anhebt? Verrichtet man auch
Arbeit, wenn man die Kiste längere Zeit in dieser Höhe hält? Handelt es sich
um Arbeit, wenn die Kiste auf gleicher Höhe entlang einer ![\unit[10]{m}](../../_images/math/5ab37424ac0a69b1ed26cd3ffad9b805b5bba0f2.png) langen, ebenen Strecke getragen wird?
langen, ebenen Strecke getragen wird?
(*) Durch eine Kraft
![F_{\mathrm{Zug}} = \unit[25]{N}](../../_images/math/4fe74f3c02da9463bf48d5f3077462b6ec71768d.png) wird ein Körper
über eine
wird ein Körper
über eine ![s = \unit[5]{m}](../../_images/math/809fd08e0de324e4cdc4cee2a6570ed8c298220e.png) lange Strecke gezogen. Welche Menge an
Arbeit wird dabei verrichtet? Wie groß ist die Arbeit der Schwerkraft auf
diesem Weg, wenn der Körper eine Gewichtskraft von
lange Strecke gezogen. Welche Menge an
Arbeit wird dabei verrichtet? Wie groß ist die Arbeit der Schwerkraft auf
diesem Weg, wenn der Körper eine Gewichtskraft von ![F_{\mathrm{G}} =
\unit[100]{N}](../../_images/math/37a492f1ecd5718c57fa39f186af5cb6c37d81c9.png) hat?
hat?
(*) Ein Gewicht mit einer Masse von
![\unit[100]{kg}](../../_images/math/be9452821f262a5e7d038160a6345abf15ebb36c.png) soll um
soll um
![\unit[1]{m}](../../_images/math/51a34f0de982f7a3c2dd6c9b85685eb17b0f71f0.png) angehoben werden. Wie viel Arbeit muss dafür aufgebracht
werden?
angehoben werden. Wie viel Arbeit muss dafür aufgebracht
werden?
(*) Ein Wanderer der Masse
![\unit[70]{kg}](../../_images/math/5d596cf8dae2c0b37653bbe7109d86666a4c4b2c.png) trägt einen
trägt einen
![\unit[7]{kg}](../../_images/math/f995215da283a0eac45b3c9039ff5d8f7db67c8e.png) schweren Rucksack auf einen um
schweren Rucksack auf einen um ![\unit[200]{m}](../../_images/math/141bb650bf1ac381009700cd2f142f1574c184ec.png) höher gelegenen Gipfel eines Berges hinauf. Wie viel Hubarbeit verrichtet er
am Rucksack, wie viel insgesamt?
höher gelegenen Gipfel eines Berges hinauf. Wie viel Hubarbeit verrichtet er
am Rucksack, wie viel insgesamt?
(**) Welche Arbeit ist nötig, um zehn auf der Erde liegende,
![h =
\unit[7]{cm}](../../_images/math/e60cfc3a1342ee991304dc62b7d4f890ca48add0.png) hohe und
hohe und ![F_{\mathrm{g}} = \unit[35]{N}](../../_images/math/0ba825d014a71621dc96ea9244a1aa9bd4479a02.png) schwere
Ziegelsteine aufeinander zu stapeln?
schwere
Ziegelsteine aufeinander zu stapeln?
(*) Durch eine Kraft
![F = \unit[15]{N}](../../_images/math/10de555af8270f2a0a79f0ab15d8215207c337d6.png) wird ein Körper über eine
wird ein Körper über eine
![s = \unit[5]{m}](../../_images/math/809fd08e0de324e4cdc4cee2a6570ed8c298220e.png) lange Strecke gezogen. Welche Menge an Arbeit wird
dabei verrichtet?
lange Strecke gezogen. Welche Menge an Arbeit wird
dabei verrichtet?
(**) Zwei Jugendliche mit den Massen
![m_1 = \unit[55]{kg}](../../_images/math/dfaceaee2ceeccd8bd41392e2fb71d213af28d70.png) und
und
![m_2 = \unit[40]{kg}](../../_images/math/507fc766ce67260d81c811e5f47475e5c78c0272.png) sitzen auf einem Schlitten und werden von einem
Pferd über ein ebenes,
sitzen auf einem Schlitten und werden von einem
Pferd über ein ebenes, ![l = \unit[200]{m}](../../_images/math/a87c4dd0b2f9cb6c7a902ce54d1aa06167406b55.png) langes Schneefeld gezogen.
Der Schlitten wiegt
langes Schneefeld gezogen.
Der Schlitten wiegt ![m_{\mathrm{S}} = \unit[5]{kg}](../../_images/math/16d4f2f3ed8e1d3eea158b5d6e5bf4d73c4ef085.png) , die Reibungszahl
von Metall auf Schnee beträgt
, die Reibungszahl
von Metall auf Schnee beträgt 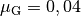 . Welche Arbeit
verrichtet das Pferd?
. Welche Arbeit
verrichtet das Pferd?
(*) Ein Fahrzeug mit einer Masse von
![m = \unit[1000]{kg}](../../_images/math/dc7396c849afeb22ed84240bd5a9589f625ecaa1.png) wird von
wird von
![v_1 = \unit[0]{m/s}](../../_images/math/46d1e48b043f2c7c398bc1a9e1a83ba2fca517b7.png) konstant auf
konstant auf ![v_2 = \unit[30]{m/s}](../../_images/math/d31bbc6cefcb4fd782359ca7af0c47a1099c43f1.png) (entspricht
(entspricht ![\unit[108]{km/h}](../../_images/math/de0714e9f5789ce1f2a08c4a2097f4b656e1bab6.png) ) beschleunigt. Wie groß ist die dabei
verrichtete Beschleunigungsarbeit?
) beschleunigt. Wie groß ist die dabei
verrichtete Beschleunigungsarbeit?
(**) Ein Fahrzeug mit einer Masse von
![m = \unit[750]{kg}](../../_images/math/7b826fb0171f17a79d5bb116224095fb6177c609.png) wird aus dem
Stand
wird aus dem
Stand ![t = \unit[10]{s}](../../_images/math/d5c779a585b5913f6b4e9672fb92c006ca4d7711.png) lang mit einer konstanten Beschleunigung
lang mit einer konstanten Beschleunigung
![a = \unitfrac[2,5]{m}{s^2}](../../_images/math/699eaa0e7046cebdb3104b7b73e07a1f11f427dd.png) beschleunigt. Wie groß ist die dabei verrichtete
Arbeit?
beschleunigt. Wie groß ist die dabei verrichtete
Arbeit?
(*) Welche Menge an Arbeit ist nötig, um ein Fahrzeug mit einer Masse von
![m=\unit[1000]{kg}](../../_images/math/4a617cfc905efdeac7e7b9ff7464c3c965d0d00f.png) von
von 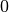 auf
auf ![\unit[50]{\frac{km}{h}}](../../_images/math/48414adf3a029eec32818d28c358f8e41ca42bd7.png) beziehungsweise von
beziehungsweise von 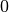 auf
auf ![\unit[100]{\frac{km}{h}}](../../_images/math/99ac0bd66194f23634d5b29aec3619b2733e99fc.png) zu
beschleunigen? Welche Menge an Arbeit ist nötig, um das Fahrzeug von
zu
beschleunigen? Welche Menge an Arbeit ist nötig, um das Fahrzeug von
![\unit[50]{\frac{km}{h}}](../../_images/math/48414adf3a029eec32818d28c358f8e41ca42bd7.png) auf
auf ![\unit[100]{\frac{km}{h}}](../../_images/math/99ac0bd66194f23634d5b29aec3619b2733e99fc.png) zu
beschleunigen?
zu
beschleunigen?
Wirkungsgrad¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Wirkungsgrad.
(*) Wie groß ist der Wirkungsgrad eines „idealen“ (also reibungsfreien und gewichtslosen) Flaschenzugs? Inwiefern gilt in diesem Fall die „Goldene Regel der Mechanik“?
(*) Das Zugseil eines Flaschenzugs wird einer Kraft von
![F =
\unit[80]{N}](../../_images/math/ad6e07aa694dbf772d7b1a9d6ea4da27ffa767bc.png) um eine Strecke
um eine Strecke ![s = \unit[7]{m}](../../_images/math/e88058a700de223e6e597c0f52be4549e23df0bc.png) angezogen. Dadurch wird
eine Last mit einer Gewichtskraft von
angezogen. Dadurch wird
eine Last mit einer Gewichtskraft von ![F_{\mathrm{G}} = \unit[250]{N}](../../_images/math/5c623ded81f25c7250aa55fa029dfbecbab5841e.png) um die Höhe
um die Höhe ![h = \unit[2]{m}](../../_images/math/016fd30615cab3f6d5327657ede07a30b4cd9da6.png) angehoben. Wie groß ist der Wirkungsgrad
angehoben. Wie groß ist der Wirkungsgrad
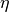 des Flaschenzugs?
des Flaschenzugs?
(*) Einem Kraftwandler mit einem Wirkungsgrad von
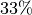 wird eine
Arbeit von
wird eine
Arbeit von ![W_{\mathrm{in}} = \unit[7200]{J}](../../_images/math/1b1bdd158ed2eeda3b7b602158603677c2462e7d.png) zugeführt. Welche Menge
an Arbeit wird dabei von dem Kraftwandler abgegeben?
zugeführt. Welche Menge
an Arbeit wird dabei von dem Kraftwandler abgegeben?
(*) Welche Menge an Arbeit muss in eine mechanische Vorrichtung mit einem Wirkungsgrad von
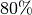 aufgewandt werden, wenn sie
aufgewandt werden, wenn sie
![W_{\mathrm{ab}} = \unit[5000]{J}](../../_images/math/edbdf088fe44e640ab4b7b6c19c471deb5c7c114.png) an Arbeit abgeben soll?
an Arbeit abgeben soll?
Mechanische Leistung¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Mechanische Leistung.
(*) Wie groß ist die Leistung eines Sportlers mit einer Masse von
![m =
\unit[70]{kg}](../../_images/math/caf0c48d22eeb90829bf94732d322bed80779c88.png) , wenn er zehn Klimmzüge mit einem Höhenunterschied von je
, wenn er zehn Klimmzüge mit einem Höhenunterschied von je
![h = \unit[0,5]{m}](../../_images/math/a2868fbd16e14f9e8cc83415ba2e12d48bb871f7.png) in einer Zeit von insgesamt
in einer Zeit von insgesamt ![t = \unit[8]{s}](../../_images/math/11d18444407c611d8901f94d6a0b4c733b664b56.png) schafft?
schafft?
(*) Welche Leistung liefert ein Motor, der eine Kiste mit einer Masse von
![\unit[200]{kg}](../../_images/math/3f5499e35faad33a8f52ae9756efd7338ebd875b.png) in
in ![t=\unit[6]{s}](../../_images/math/7723bcbfae4ac9ff3bc18c3606b633bb535a80d3.png) auf eine Höhe von
auf eine Höhe von
![h=\unit[4]{m}](../../_images/math/20a111bdc3922be5b6a22e1480992392444dd813.png) anheben kann?
anheben kann?
(*) Welche Masse kann durch eine Leistung von
![P = \unit[1]{PS} =
\unit[735]{W}](../../_images/math/b53edd5f4f79b486781bdd400812e55c396d685b.png) in einer Sekunde um einen Meter angehoben werden?
in einer Sekunde um einen Meter angehoben werden?
(**) Ein Löschfahrzeug der Feuerwehr pumpt mit einer Leistung von
![\unit[5]{kW}](../../_images/math/b83f258e39d49235a7c98f5e6d68a2edd81b4909.png) Wasser in
Wasser in ![h = \unit[15]{m}](../../_images/math/6bd9a512015a5e936941122be10c36052f0feebe.png) Höhe. Wie viel Liter
Wasser stehen den Feuerwehrleuten in einer Sekunde, wie viel in einer Minute
zur Verfügung?
Höhe. Wie viel Liter
Wasser stehen den Feuerwehrleuten in einer Sekunde, wie viel in einer Minute
zur Verfügung?
(**) Zum Ziehen eines Schlittens sei eine horizontale Kraft von
![F =
\unit[300]{N}](../../_images/math/dbecd3ed0997ab657f7a0794d0c65c8afca0d3a2.png) nötig. Wie groß ist die mechanische Leistung, wenn der
Schlitten mit
nötig. Wie groß ist die mechanische Leistung, wenn der
Schlitten mit ![v = \unit[0,75]{m/s}](../../_images/math/bca6d69fd5a904dcb399ad12359f82fc7242128c.png) gezogen wird?
gezogen wird?
(**) Ein Fahrzeug der Masse
![m = \unit[1200]{kg}](../../_images/math/225b748d9f83fbb13a0d937db8a07d0946059e29.png) wird beim Einfahren
auf eine Autobahn in
wird beim Einfahren
auf eine Autobahn in ![\unit[t=8]{s}](../../_images/math/188045205e5ad03a82dbb10f08cc66245d5060fd.png) konstant von
konstant von
![\unit[15]{\frac{m}{s}}](../../_images/math/b590746bbc440f24e49c03c4e4f1bf6fcb8b2c79.png) auf
auf ![\unit[25]{\frac{m}{s}}](../../_images/math/46e6c695747a07a330e8a3716aa8cb1e68db7fcf.png) beschleunigt. Wie groß muss die Beschleunigungs-Leistung des Motors dabei
mindestens sein?
beschleunigt. Wie groß muss die Beschleunigungs-Leistung des Motors dabei
mindestens sein?
Mechanische Energie¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Mechanische Energie.
(*) Wie viel Energie besitzt
![\unit[1]{m^3}](../../_images/math/5c3e8b7983236a2f9d05a7885cc7f11b95715d89.png) Wasser
Wasser ![(m =
\unit[1000]{kg})](../../_images/math/e6ae065fbe6f3dbfa9227bc26918e53a9da0bce2.png) , das aus einem Stausee
, das aus einem Stausee ![h = \unit[120]{m}](../../_images/math/af3b33bbf82c4f20a518a46979633ab904fe9470.png) tief hinab fließt?
tief hinab fließt?
(*) Ein PKW mit einer Masse von
![m_{\mathrm{PKW}} = \unit[1\,000]{kg}](../../_images/math/54928f114b1fcad92f6700504cbf348c849075d6.png) und ein LKW mit einer Masse von
und ein LKW mit einer Masse von ![m_{\mathrm{LKW}} = \unit[8\,000]{kg}](../../_images/math/51b96ec88ac893a79d9d453c94249ef7c93e4bdf.png) fahren jeweils
fahren jeweils ![v_1 = \unit[50]{km/h}](../../_images/math/d51a970a44477d2fcb401072c67ae7e4a2ee9cc7.png) . Wie groß sind die
Bewegungsenergien der beiden Fahrzeuge? Wie groß ist die Bewegungsenergie des
PWKs, wenn seine Geschwindigkeit verdoppelt bzw. verdreifacht wird?
. Wie groß sind die
Bewegungsenergien der beiden Fahrzeuge? Wie groß ist die Bewegungsenergie des
PWKs, wenn seine Geschwindigkeit verdoppelt bzw. verdreifacht wird?
(**) Angenommen, ein Fahrzeug würde mit
![v = \unitfrac[72]{km}{h}](../../_images/math/3b98d34a1e32861a2167f7fb35d7451eaf5c5378.png) gegen ein
festes Hindernis prallen. Aus welcher Höhe müsste das Fahrzeug stürzen, um
– bei Vernachlässigung des Luftwiderstands – eine vergleichbare Wirkung
zu erfahren?
gegen ein
festes Hindernis prallen. Aus welcher Höhe müsste das Fahrzeug stürzen, um
– bei Vernachlässigung des Luftwiderstands – eine vergleichbare Wirkung
zu erfahren?
(**) Ein Badegast springt von einem 5-m-Turm ins Wasser. Wie groß ist seine Geschwindigkeit
 beim Eintauchen, wenn der Luftwiderstand
vernachlässigt werden kann?
beim Eintauchen, wenn der Luftwiderstand
vernachlässigt werden kann?
(*) Stimmt es, dass alle Lebensmittel gespeicherte Sonnen-Energie beinhalten?
(*) Welche Energieumwandlungen finden beim Trampolinspringen statt?

