Kraftwandler und Getriebe¶
Hebel¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Hebel.
(*) Funktioniert eine Balkenwaage auch auf dem Mond? Gilt das gleiche auch für eine Federkraftwaage?
(*) Weshalb ist weniger Kraft nötig, um Deckel einer Farbdose mit Hilfe eines Schraubenziehers zu öffnen, wenn dieser unter dem Deckelrand angesetzt wird?
Beispiel: Wie groß ist die Kraft
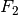 auf den Deckel, wenn der Abstand vom
Dosenrand zum Griff des Schraubenziehers
auf den Deckel, wenn der Abstand vom
Dosenrand zum Griff des Schraubenziehers ![s_2=\unit[0,16]{m}](../../_images/math/1a931b88ba8fd7e9db792276dc2cc4da76d48b79.png) , der Abstand
vom Dosenrand zum Deckel
, der Abstand
vom Dosenrand zum Deckel ![s_2=\unit[0,01]{m}](../../_images/math/8e8b59db892677c7af06ef7de6d07ebbfc7c936a.png) und die am Griff
angreifende Kraft
und die am Griff
angreifende Kraft ![F_1 = \unit[5]{N}](../../_images/math/3e31df6fc57870c26a3d1246e8104a4e37da468c.png) beträgt?
beträgt?
(*) An einer Balkenwaage hängt im Abstand
![s_1 = \unit[10]{cm}](../../_images/math/ab933cf7c7039f44327fc85b26cb867a05ea2fc0.png) eine Last
eine Last ![m_1 = \unit[2]{kg}](../../_images/math/fd0d7bb06de48bd9634563147e1033de89f1bd86.png) . In welchem Abstand zur Drehachse
muss man ein Gegengewicht mit einer Masse von
. In welchem Abstand zur Drehachse
muss man ein Gegengewicht mit einer Masse von ![m_2 =
\unit[500]{g}](../../_images/math/f1c83301b6863f6405045ea07006374b5d869a71.png) anbringen, damit die Waage im Gleichgewicht ist?
anbringen, damit die Waage im Gleichgewicht ist?
(*) Eine Person hält ein
![m = \unit[2]{kg}](../../_images/math/2f34a208a0187678cc2c75ae7810051e53686fc3.png) schweres Gewicht mit horizontal
gehaltenem Unterarm in der Hand (der Oberarm hängt dabei lose nach unten). Der
Anriffspunkt des Muskels am Unterarm ist
schweres Gewicht mit horizontal
gehaltenem Unterarm in der Hand (der Oberarm hängt dabei lose nach unten). Der
Anriffspunkt des Muskels am Unterarm ist ![s_1 = \unit[5]{cm}](../../_images/math/1bc67cd0f9dc3ab5e4c3780429ce1e783b773273.png) vom
Drehpunkt im Ellenbogen entfernt, der Abstand der Hand zum Drehpunkt beträgt
vom
Drehpunkt im Ellenbogen entfernt, der Abstand der Hand zum Drehpunkt beträgt
![s_2 = \unit[35]{cm}](../../_images/math/3f7632599f6f4979143b37a3100558cba02377df.png) . Welche Kraft
. Welche Kraft 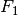 muss der Muskel
aufbringen, um den Unterarm in horizontaler Position zu halten?
muss der Muskel
aufbringen, um den Unterarm in horizontaler Position zu halten?
(**) An der linken Seite eines zweiseitigen Hebels sind zwei Gewichte
![F
_{\mathrm{1}} = \unit[3,5]{N}](../../_images/math/152adc8ffe071cc901e0e1dbd9b479cd99a6aab1.png) und
und ![m_2 = \unit[5]{N}](../../_images/math/c0c2bf19c7d30cb0aed7a4280729e05befd336ee.png) im Abstand
im Abstand
![s_1 = \unit[0,2]{m}](../../_images/math/1bb5a164bb381597541984d0c8ad6287f83c70c7.png) bzw.
bzw. ![s_2 = \unit[0,1]{m}](../../_images/math/0aaf084cbbaf1050e6731c4c88956dddc468ad6c.png) von der Drehachse befestigt. Am rechten Arm sind zwei Gewichte
von der Drehachse befestigt. Am rechten Arm sind zwei Gewichte ![F
_{\mathrm{3}} = \unit[1,5]{N}](../../_images/math/273201f07d20621a36b2b2d072470883cdcda322.png) und
und ![m_4 = \unit[4]{N}](../../_images/math/f874ad98503e6e808f21946226ea2edf1a53c340.png) im Abstand
im Abstand
![s_3 = \unit[0,6]{m}](../../_images/math/9b3ae6fcfa9944e5f4e37d99ced7970ef7d83df8.png) bzw.
bzw. ![s_4 = \unit[0,075]{m}](../../_images/math/d73b3babe1953feb67af7f072e6c42c24ade2138.png) angebracht. Befindet sich der Hebel im Gleichgewicht?
angebracht. Befindet sich der Hebel im Gleichgewicht?
Schiefe Ebene¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Schiefe Ebene.
(*) Eine Schubkarre mit einer Gewichtskraft von
![\unit[600]{N}](../../_images/math/231042863ef4440bf0c4874362f6092d9dd34bae.png) wird
entlang einer schiefen Ebene verschoben. Die schiefe Ebene ist
wird
entlang einer schiefen Ebene verschoben. Die schiefe Ebene ist
![\unit[2,4]{m}](../../_images/math/beb8b922ca3c1a6e068f7b5aeb6b2e2cecaca45b.png) lang, ihre Höhe beträgt
lang, ihre Höhe beträgt ![\unit[0,6]{m}](../../_images/math/897a2f5d074a33ddec192298ff5fae0aa3910bca.png) . Wie groß
ist die zum (reibungsfreien) Schieben der Schubkarre notwendige Kraft
. Wie groß
ist die zum (reibungsfreien) Schieben der Schubkarre notwendige Kraft
 ?
?
Flaschenzüge und Rollen¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Flaschenzügen und Rollen.
(*) Mit einem Flaschenzug aus vier losen und und vier festen Rollen wird eine Last der Masse
![m=\unit[200]{kg}](../../_images/math/9c3ec3d7ff8b13230fd1c451cff4020578311282.png) um eine Höhe von
um eine Höhe von ![h =
\unit[3]{m}](../../_images/math/b02f0d3d4665bd3226bb6110f0e79dd2b8a998f0.png) angehoben. Die Masse einer einzelnen Rolle beträgt
angehoben. Die Masse einer einzelnen Rolle beträgt
![\unit[5]{kg}](../../_images/math/463601bf8407446b44b766c72285226ddc8215e3.png) . Wie groß ist die Zugkraft
. Wie groß ist die Zugkraft  , wie lang die
Zugstrecke
, wie lang die
Zugstrecke  ?
?
(*) Welche Masse kann eine Person, die selbst
![\unit[50]{kg}](../../_images/math/ace271226a971d2a199f66cd92cc0e82f4d9675c.png) wiegt, durch
ihre Gewichtskraft mit Hilfe eines Flaschenzugs aus zwei festen und zwei losen
Rollen anheben, wenn das Gewicht des Flaschenzugs und die in den Rollen
auftretende Reibung vernachlässigt werden können?
wiegt, durch
ihre Gewichtskraft mit Hilfe eines Flaschenzugs aus zwei festen und zwei losen
Rollen anheben, wenn das Gewicht des Flaschenzugs und die in den Rollen
auftretende Reibung vernachlässigt werden können?
(**) Eine Anordnung, wie sie in der folgenden Abbildung dargestellt ist, heißt „Potenzflaschenzug“. Mit welcher Kraft
 muss am losen Seilende
mindestens gezogen werden, um eine Last mit einem Gewicht von
muss am losen Seilende
mindestens gezogen werden, um eine Last mit einem Gewicht von
![F_{\mathrm{G}} = \unit[800]{N}](../../_images/math/6fdd9c4b86920a7abc9a48be4da9235935077645.png) anzuheben? Mit welcher Kraft muss man am
losen Seilende ziehen, wenn man die Gewichtskraft
anzuheben? Mit welcher Kraft muss man am
losen Seilende ziehen, wenn man die Gewichtskraft ![F_{\mathrm{G,R}} =
\unit[20]{N}](../../_images/math/71677a59f26399460630b9d49ac6c99284ba68b3.png) jeder einzelnen Rolle berücksichtigt? (Der Einfluss von
Reibungskräften wird bei dieser Aufgabe nicht berücksichtigt.)
jeder einzelnen Rolle berücksichtigt? (Der Einfluss von
Reibungskräften wird bei dieser Aufgabe nicht berücksichtigt.)
Zahnräder und Getriebe¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Zahnräder und Getriebe.
(**) An einem Fahrrad wird die Kraft von den Pedalen mittels dem Pedal und der Kurbel, dem vorderen Zahnrad, der Kette und schließlich dem hinteren Zahnrad auf das Hinterrad übertragen. Wie groß ist die auf ein Hinterrad mit einem Radius von
![r_4 = \unit[0,35]{m}](../../_images/math/a3c432544067165a80a7f9e3ba01ba875ca78f45.png) wirkende Kraft
wirkende Kraft 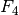 , wenn der
Radfahrers auf eine
, wenn der
Radfahrers auf eine ![r_1 = \unit[0,2]{m}](../../_images/math/97efe320eb0d3c97726ebb33380503b4031818eb.png) lange Kurbel eine senkrechte
Kraft von
lange Kurbel eine senkrechte
Kraft von ![F_1 = \unit[50]{N}](../../_images/math/75ad86317c69d17efe00e86df6d643945dc9f54b.png) ausübt, der Umfang des vorderen
Zahnkranz einen Radius von
ausübt, der Umfang des vorderen
Zahnkranz einen Radius von ![r_2 = \unit[0,1]{m}](../../_images/math/d22dc5a27371b8cb14b0fce49dff453f83c6d3b5.png) und der hintere
Zahnkranz einen Radius von
und der hintere
Zahnkranz einen Radius von ![r_3 = \unit[0,05]{m}](../../_images/math/8013e2a1878c3c9e1138a7ea0b48f787680e541e.png) hat?
hat?
Wie groß ist im Vergleich die auf das Hinterrad wirkende Kraft
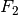 ,
wenn der Fahrer vorne auf einen kleineren Zahnkranz mit Radius
,
wenn der Fahrer vorne auf einen kleineren Zahnkranz mit Radius ![r_2 =
\unit[0,05]{m}](../../_images/math/e6b5bcddfe48265f13caca91069778553fb55405.png) herunter schaltet und die gleiche Kraft auf das Pedal ausübt?
herunter schaltet und die gleiche Kraft auf das Pedal ausübt?
