Hebel¶
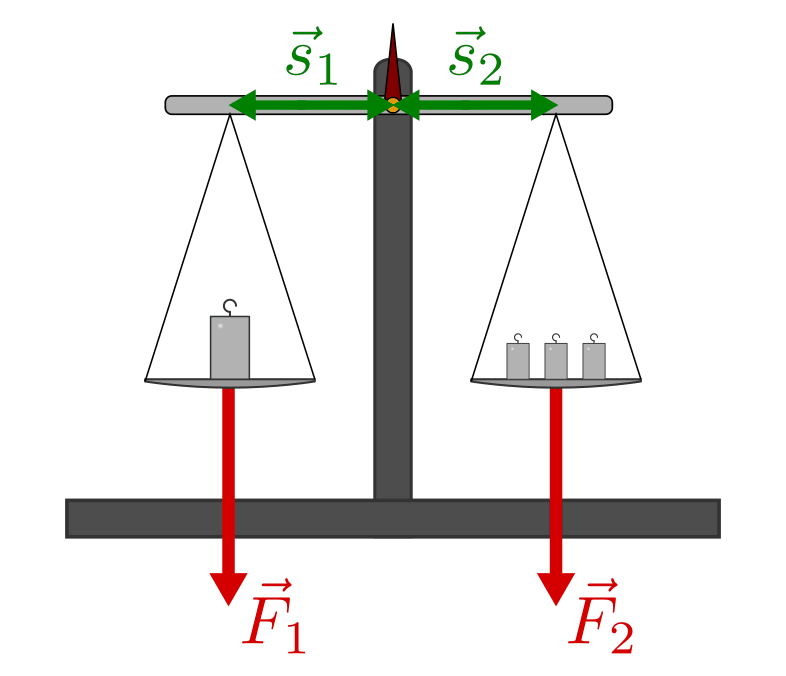
Ein Hebel ist ein starrer, meist stabförmiger Körper, der sich und um eine feste Achse drehen lässt (z.B. eine Wippe). Hebel werden beispielsweise dazu genutzt, um mit einer kleinen Kraft einen Körper mit großem Gewicht zu heben.

Die Wippe als (zweiseitiger) Hebel: Nicht nur die wirkende Kraft, auch der Abstand zur Drehachse ist von Bedeutung.
Die Stelle, an der eine Kraft 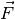 am Hebel wirkt, heißt Angriffspunkt der
Kraft, der Abstand ihrer Wirkungslinie zur Drehachse wird Kraftarm
am Hebel wirkt, heißt Angriffspunkt der
Kraft, der Abstand ihrer Wirkungslinie zur Drehachse wird Kraftarm  genannt.
genannt.
Wirken auf einen Hebel zwei Kräfte 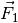 und
und 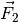 , so
ist der Hebel dann im Gleichgewicht, wenn das Produkt ersten Kraft
, so
ist der Hebel dann im Gleichgewicht, wenn das Produkt ersten Kraft
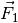 mit ihrem Kraftarm
mit ihrem Kraftarm 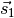 gleich dem Produkt der
zweiten Kraft
gleich dem Produkt der
zweiten Kraft 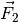 mit ihrem Kraftarm
mit ihrem Kraftarm 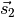 ist:
ist:
(1)¶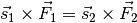
Die obige Formel, die formal eine Gleichheit zweier Drehmomente beschreibt, wird auch als Hebelgesetz bezeichnet. Es gilt für alle Hebelformen gleichermaßen.
Zweiseitige Hebel¶
An einem zweiseitigen Hebel liegen die Angriffspunkte der Kräfte, von der Drehachse aus betrachtet, auf verschiedenen Seiten des Hebels.
Der Hebel ist im Gleichgewicht, wenn das Drehmoment 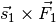 auf der linken Seite des Hebels dem Drehmoment
auf der linken Seite des Hebels dem Drehmoment 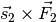 auf der rechten Seite des Hebels entspricht.[1] Ist das
wirkende Drehmoment auf der einen Seite größer als auf der anderen, so führt die
Hebelstange eine entsprechende Rotation um die Drehachse aus.
auf der rechten Seite des Hebels entspricht.[1] Ist das
wirkende Drehmoment auf der einen Seite größer als auf der anderen, so führt die
Hebelstange eine entsprechende Rotation um die Drehachse aus.
Einseitige Hebel¶
An einem einseitigen Hebel liegt die Drehachse am Rand der Hebelstange, so dass die Angriffspunkte aller wirkenden Kräfte, von der Drehachse aus betrachtet, auf der gleichen Seite des Hebels liegen.
Damit an einem einseitigen Hebel ein Gleichgewicht herrschen kann, muss wiederum die Summe der linksdrehenden Drehmomente gleich der Summe der rechtsdrehenden Drehmomente entsprechen. Dazu müssen die auf einen einseitigen Hebel einwirkenden Kräfte in entgegengesetzte Richtungen zeigen.[2]
Ein markantes Beispiel für einen einseitigen Hebel ist der menschliche Unterarm. Der Ellenbogen wirkt als Drehachse, die Gewichtskraft des zu tragenden Gegenstands wirkt nach unten, die Muskelkraft des Biceps nach oben. Da der Biceps-Muskel um ein Vielfaches näher an der Drehachse am Unterarm angreift als das zu tragende Gewicht, muss die dort wirkende Kraft um ein entsprechendes Vielfaches größer sein.
Winkelhebel¶
Ein Hebel mit einer gewinkelten Stange wird Winkelhebel genannt. Je nachdem, an welcher Stelle sich die Drehachse befindet, gleicht ein Winkelhebel einem einseitigen oder zweiseitigen Hebel.
Das Hebelgesetz 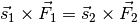 gilt auch bei einem Winkelhebel unverändert. Ist das linksdrehende Drehmoment
gleich dem rechtsdrehenden, so herrscht ein Hebel-Gleichgewicht; andernfalls
tritt eine entsprechende Rotation um die Drehachse auf.
gilt auch bei einem Winkelhebel unverändert. Ist das linksdrehende Drehmoment
gleich dem rechtsdrehenden, so herrscht ein Hebel-Gleichgewicht; andernfalls
tritt eine entsprechende Rotation um die Drehachse auf.
Wellrad und Kurbel¶
Ein Wellrad besteht aus (mindestens) zwei verschieden großen und miteinander verbundenen Rädern, die fest auf einer Achse („Welle“) sitzen. Die Felgen der Räder können dabei aus einem massiven Material bestehen, oder über Speichen mit der Achse verbunden sein.
Prinzipiell handelt es sich auch bei einem Wellrad um einen Hebel[3], so dass im Gleichgewichtsfall wiederum das allgemeine Hebelgesetz gilt:
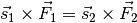
Dabei entsprechen die Wegstrecken 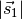 und
und 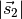 den Radien der beiden Räder. Betraglich ist die Kraftverstärkung, die bei einer
Drehung des äußeren Rades gegenüber dem inneren Rad auftritt, gleich dem
Verhältnis der Radien beider Räder:
den Radien der beiden Räder. Betraglich ist die Kraftverstärkung, die bei einer
Drehung des äußeren Rades gegenüber dem inneren Rad auftritt, gleich dem
Verhältnis der Radien beider Räder:
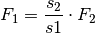
Eine kleine Kraft am großen Rad hat somit eine große Kraft am kleinen Rad zur Folge. Nach dem gleichen Prinzip funktioniert auch eine Kurbel. Diese kann man sich als einzelne, massive Speiche eines Wellrades vorstellen.
Beispiel:
- Eine Kurbel mit einem Radius von
![r_2 = \unit[25]{cm}](../../_images/math/bc5edd66ee661eaf62ddd9785eded705d61c73f1.png) wird mit
einer Kraft von
wird mit
einer Kraft von ![F_2 = \unit[100]{N}](../../_images/math/d039267f63f362e70d319945b5a848044eceba94.png) angetrieben. Die Kraft,
die dadurch auf ein Antriebsrad mit Radius
angetrieben. Die Kraft,
die dadurch auf ein Antriebsrad mit Radius ![r_1 = \unit[5]{cm}](../../_images/math/148a067b85bb7f0d6e354df8d3be6cfc327a698c.png) wirkt, beträgt somit:
wirkt, beträgt somit:
![F_1 \cdot r_1 = F_2 \cdot r_2 \quad
\Leftrightarrow \quad F_1 = \frac{F_2 \cdot r_2}{r_1} \\[5pt]
F_1 = \frac{\unit[100]{N} \cdot \unit[0,25]{m}}{\unit[0,05]{m}} =
\unit[500]{N}](../../_images/math/8c2b9dff7333c4236e67ed6beca81c87e97c6fb0.png)
Auch in diesem Fall bewirkt eine kleine Kraft an der langen Pedalstange eine große Kraft am kleinen Antriebsrad.
Anmerkungen:
| [1] | Wirken auf eine Seite der Hebelstange mehrere Kräfte ein, so entspricht das Drehmoment auf dieser Seite der Summe der einzelnen Drehmomente. |
| [2] | Wirkt eine Kraft nicht senkrecht auf einen Hebel ein, so muss sie, wie in Abschnitt Kraftzerlegung in Teilkräfte beschrieben, in eine Teilkraft senkrecht und eine zweite Teilkraft parallel zur Hebelstange aufgeteilt werden. Für das wirkende Drehmoment ist nur der senkrechte Anteil der Kraft von Bedeutung. |
| [3] | Je nachdem, an welchen Stellen das Seil an den beiden Rädern verknotet ist, kann es sich beim Wellrad um einen einseitigen bzw. zweiseitigen Winkel oder auch um einen Winkelhebel handeln. Die Funktionsweise des Wellrads bleibt dabei unverändert. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.