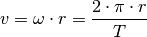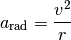Kreisförmige Bewegungen¶
Eine kreisförmige Bewegung ist die Bewegung eines Körpers auf einer Kreisbahn. Da einzelne Teile des Körpers dabei unterschiedlich lange Strecken zurücklegen, wird im Allgemeinen nur die Bewegung seines Schwerpunkts betrachtet.
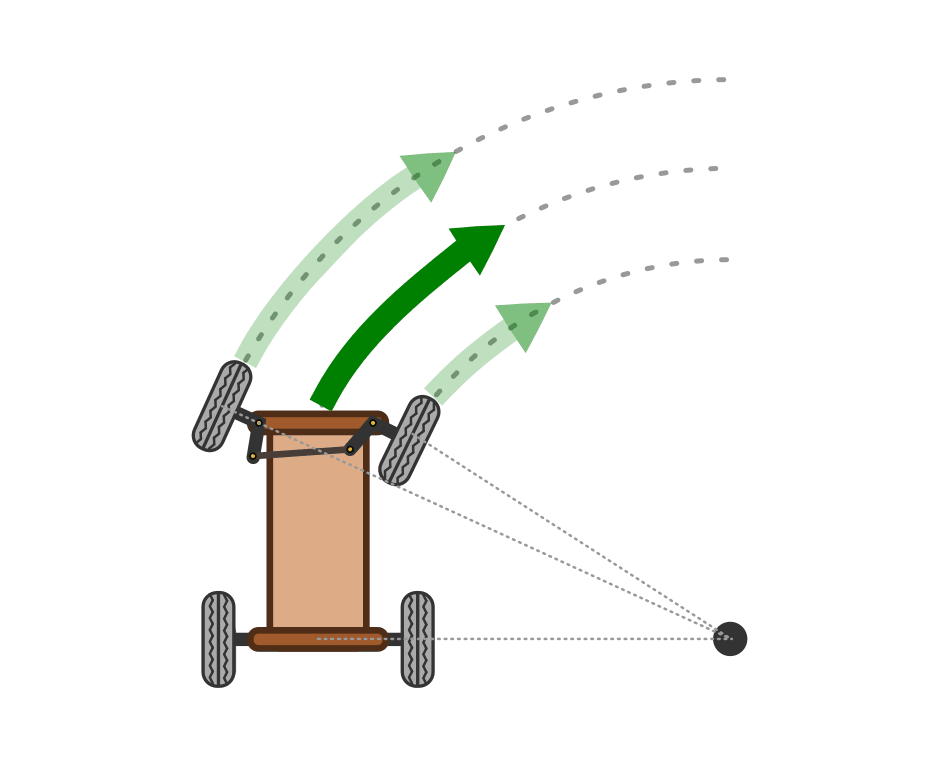
Entlang einer Kreisbahn legen die Räder auf der Innen- und Außenspur unterschiedlich weite Strecken zurück.
Rotationen
Prinzipiell gibt es keinen Unterschied zwischen einer kreisförmigen Bewegung und einer Rotation. Im Sprachgebrauch bezeichnet man allerdings eine Bewegung als kreisförmig, wenn der Radius der Kreisbahn groß ist im Vergleich zu den Abmessungen des sich bewegenden Körpers; ist der Radius der kreisförmigen Bewegung hingegen in der gleichen Größenordnung wie die Länge des Körpers, so spricht man von einer Rotation.
Kreisförmige Bewegungen mit konstanter Geschwindigkeit¶
Bei einer gleichförmigen Kreisbewegung ändert sich ständig die Richtung, in die
sich der Körper bewegt, jedoch nicht der Betrag seiner Geschwindigkeit.
Eine volle Umdrehung entspricht dabei einem Winkel von 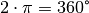 , bei einer Umlaufbahn mit dem Radius
, bei einer Umlaufbahn mit dem Radius  beträgt die dabei vom Körper
zurückgelegte Strecke
beträgt die dabei vom Körper
zurückgelegte Strecke 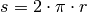 .
.
Winkelgeschwindigkeit und Drehzahl
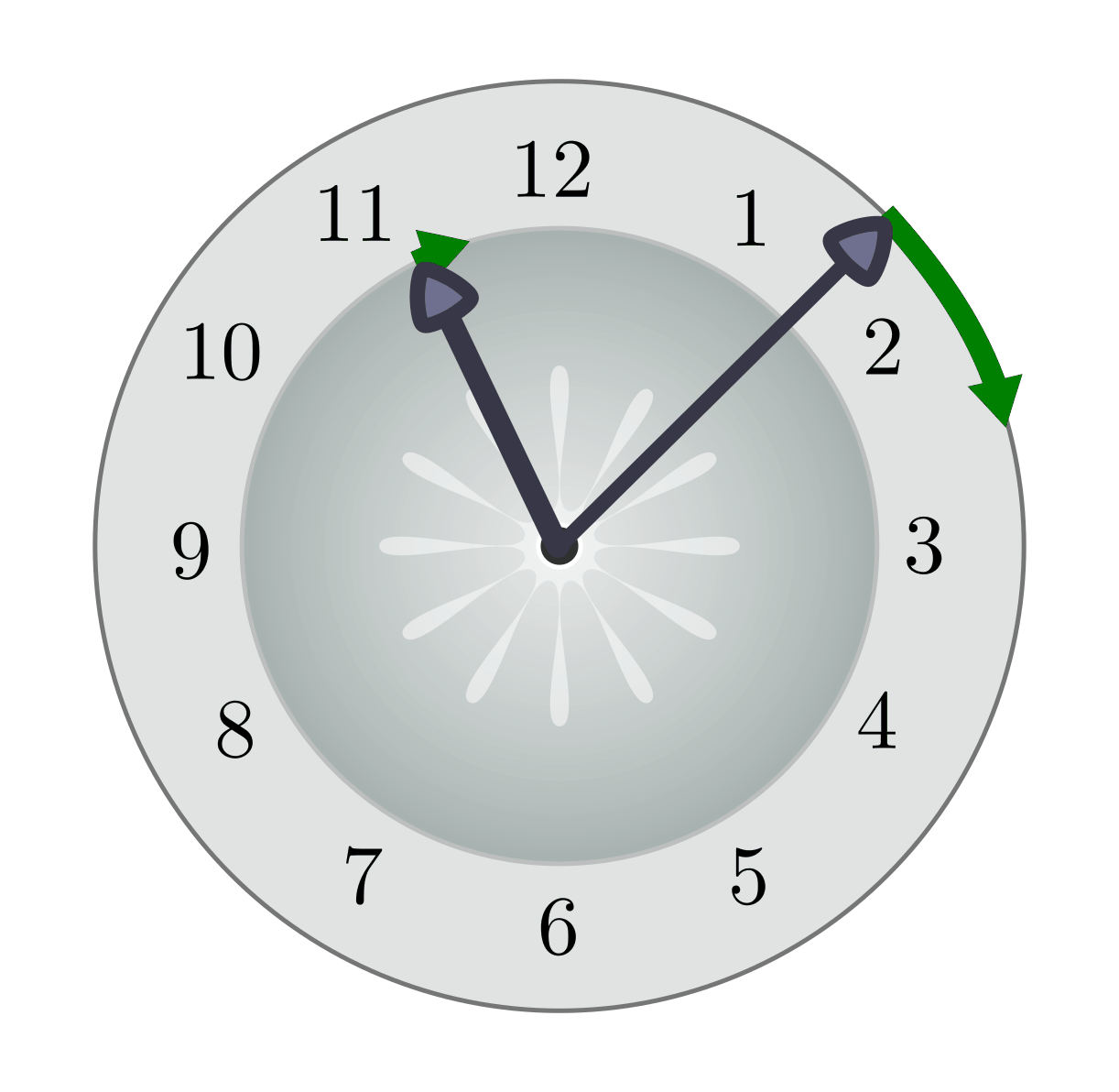
Bei einer kreisförmigen Bewegung mit konstanter Geschwindigkeit überstreicht der Ortsvektor des Körpers – ausgehend vom Mittelpunkt der Kreisbewegung – in gleichen Zeitabschnitten einen jeweils gleichen Winkel.
Definition:
Die Winkelgeschwindigkeit (auch „Drehgeschwindigkeit“ oder „Kreisfrequenz“ genannt)
eines Körpers ist gleich dem Verhältnis aus dem durchlaufenen Winkel
und der dazu benötigten Zeit
:
Zur Bestimmung der Winkelgeschwindigkeit wird häufig eine komplette Umdrehung
in Relation zu der dafür benötigten Umlaufzeit
gesetzt:
(1)¶
Die Winkelgeschwindigkeit ist umso schneller, desto kleiner der Wert der Umlaufzeit
ist.
Einheit:
Die Winkelgeschwindigkeit ist, wie auch die Bahngeschwindigkeit, eine vektorielle Größe. Da bei einer gleichmäßigen Kreisbewegung die Winkelgeschwindigkeit konstant bleibt, existiert für diese nur eine mögliche Richtung, die ebenfalls unverändert bleibt, und zwar senkrecht zur Drehebene.
Als Merkregel für die Orientierung von 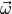 kann die
„Rechte-Hand-Regel“ genutzt werden: Zeigen die Finger der rechten Hand in
Richtung der Drehbewegung, so zeigt der Daumen die Richtung der
Winkelgeschwindigkeit an.
kann die
„Rechte-Hand-Regel“ genutzt werden: Zeigen die Finger der rechten Hand in
Richtung der Drehbewegung, so zeigt der Daumen die Richtung der
Winkelgeschwindigkeit an.
Neben der Winkelgeschwindigkeit wird bei Dreh- und Rotationsbewegungen häufig
auch eine sogenannte „Drehzahl“  angegeben, welche die Anzahl an
vollständigen Umdrehungen je Zeiteinheit angibt. Zwischen der Drehzahl
angegeben, welche die Anzahl an
vollständigen Umdrehungen je Zeiteinheit angibt. Zwischen der Drehzahl
 und der Winkelgeschwindigkeit
und der Winkelgeschwindigkeit  gilt folgender
Zusammenhang:
gilt folgender
Zusammenhang:
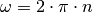
Der Faktor 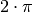 ergibt sich daraus, dass eine vollständige
Umdrehung einem Winkel von
ergibt sich daraus, dass eine vollständige
Umdrehung einem Winkel von 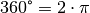 entspricht.
Da Winkelangaben reine Zahlenwerte sind, wird eine Drehzahl von beispielsweise
zehn Umdrehungen je Minute als
entspricht.
Da Winkelangaben reine Zahlenwerte sind, wird eine Drehzahl von beispielsweise
zehn Umdrehungen je Minute als ![n = \unit[10]{\frac{1}{min}}](../../_images/math/46b9964a0b05e9afb1f31132089ad722798d604e.png) geschrieben.
Wenn allerdings nur
geschrieben.
Wenn allerdings nur ![\unit[10]{\frac{1}{min}}](../../_images/math/aca8297455864eb82c048087868904081ad8529a.png) als Bezeichnung angegeben
wird, so kann anhand der Einheit nicht zweifelsfrei abgelesen werden, ob damit
eine Winkelgeschwindigkeit oder eine Drehzahl gemeint ist. In der Praxis wird
die Drehzahl daher häufig in der Form
als Bezeichnung angegeben
wird, so kann anhand der Einheit nicht zweifelsfrei abgelesen werden, ob damit
eine Winkelgeschwindigkeit oder eine Drehzahl gemeint ist. In der Praxis wird
die Drehzahl daher häufig in der Form ![n = \unit[10]{\frac{U}{min}}](../../_images/math/578d91bdc5324e9d48d3b54c8de9eaeb90a56a06.png) angegeben, wobei
angegeben, wobei 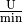 für „Umdrehungen je Minute“
steht.
für „Umdrehungen je Minute“
steht.
Bahngeschwindigkeit
Je weiter ein rotierender Punkt oder ein sich auf einer Kreisbahn bewegender Körper von der Rotationsachse entfernt ist, desto weitere Strecken legt er bei gleicher Winkelgeschwindigkeit zurück.
Definition:
Die Bahngeschwindigkeit
eines Körpers auf einer Kreisbahn ist gleich dem Produkt aus seiner Winkelgeschwindigkeit
und dem Radius
der Kreisbahn:
(2)¶
Einheit:
Die Bahngeschwindigkeitin Meter je Sekunde
oder in Kilometer je Stunde
angegeben.
Radialbeschleunigung
Da sich die Richtung der Bahngeschwindigkeit eines mit konstanter
Winkelgeschwindigkeit  beziehungsweise konstanter
Bahngeschwindigkeit
beziehungsweise konstanter
Bahngeschwindigkeit  umlaufenden Punktes ständig ändert, erfährt jeder
Körper auf einer Kreisbahn eine zeitlich konstante Radialbeschleunigung
umlaufenden Punktes ständig ändert, erfährt jeder
Körper auf einer Kreisbahn eine zeitlich konstante Radialbeschleunigung
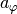 in Richtung des Kreismittelpunktes.
in Richtung des Kreismittelpunktes.
Definition:
Die Radialbeschleunigung
ist direkt proportional zum Quadrat der Bahngeschwindigkeit
und umgekehrt proportional zum Kreisradius
:
(3)¶
Einheit:
Die Zentripetalbeschleunigungwird in Meter je Quadratsekunde
angegeben.
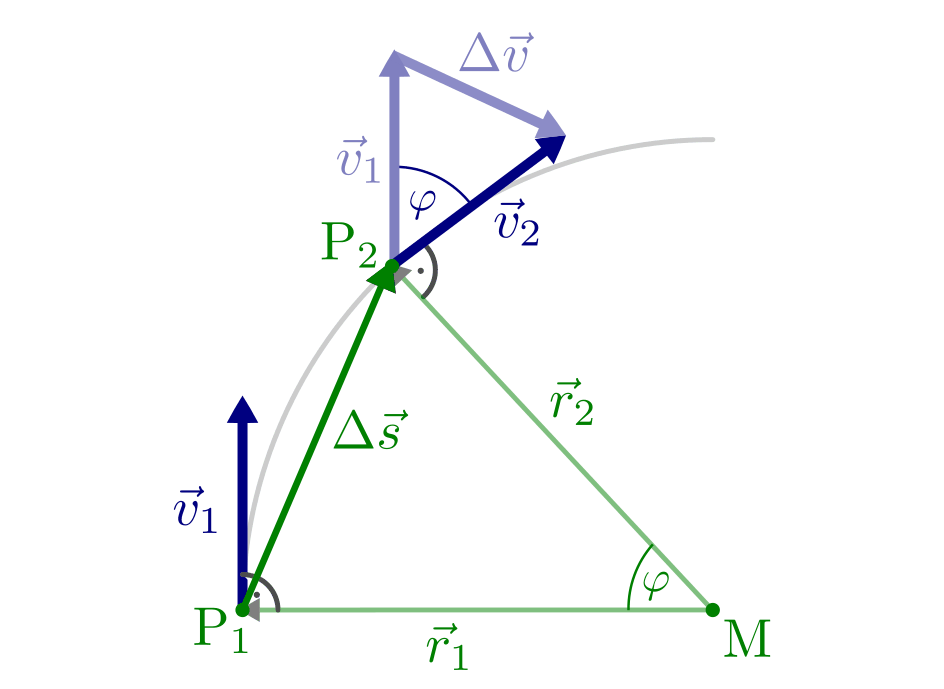
Die obige Formel für die Radialbeschleunigung lässt sich herleiten, wenn man in
einer schematischen Abbildung zu den zwei Ortspunkten 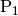 und
und
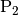 eines sich auf einer Kreisbahn bewegenden Körpers die
zugehörigen Bahngeschwindigkeiten
eines sich auf einer Kreisbahn bewegenden Körpers die
zugehörigen Bahngeschwindigkeiten 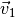 und
und 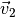 einzeichnet. Diese ändern aufgrund der Radialbeschleunigung zwar ihre Richtung,
jedoch nicht ihren Betrag, so dass
einzeichnet. Diese ändern aufgrund der Radialbeschleunigung zwar ihre Richtung,
jedoch nicht ihren Betrag, so dass 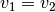 gilt. Beide
Bahngeschwindigkeiten stehen zudem stets senkrecht zur jeweiligen Radiuslinie;
bewegt sich also der Körper entlang der Kreisbahn um den Winkel
gilt. Beide
Bahngeschwindigkeiten stehen zudem stets senkrecht zur jeweiligen Radiuslinie;
bewegt sich also der Körper entlang der Kreisbahn um den Winkel 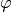 weiter, so dreht sich auch sein Geschwindigkeitsvektor um den gleichen Winkel.
weiter, so dreht sich auch sein Geschwindigkeitsvektor um den gleichen Winkel.
Da der Abstand 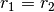 der Punkte
der Punkte 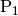 und
und 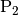 vom Kreismittelpunkt gleich ist, haben das grün dargestellte Orts-Dreieck und
das blau dargestellte Geschwindigkeits-Dreieck neben dem gleichen Winkel
vom Kreismittelpunkt gleich ist, haben das grün dargestellte Orts-Dreieck und
das blau dargestellte Geschwindigkeits-Dreieck neben dem gleichen Winkel
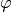 zudem ein gleiches Längenverhältnis zweier Seiten, denn es gilt
zudem ein gleiches Längenverhältnis zweier Seiten, denn es gilt
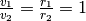 .[1] Beide Dreiecke sind also
einander ähnlich und stimmen somit in den
Längenverhältnissen aller Seiten überein. Folglich gilt:
.[1] Beide Dreiecke sind also
einander ähnlich und stimmen somit in den
Längenverhältnissen aller Seiten überein. Folglich gilt:

Setzt man diesen Ausdruck für die Geschwindigkeitsänderung 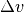 in Relation zur dafür benötigten Zeit
in Relation zur dafür benötigten Zeit 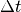 , so erhält man die
Gleichung (3) für die Radialbeschleunigung:
, so erhält man die
Gleichung (3) für die Radialbeschleunigung:
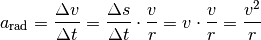
Auch bei einer konstanten Bahngeschwindigkeit ist eine Kreisbewegung stets eine
beschleunigte Bewegung: Es ändert sich zwar nicht der Betrag 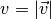 der Geschwindigkeit, dafür aber kontinuierlich ihre Richtung.
der Geschwindigkeit, dafür aber kontinuierlich ihre Richtung.
Kreisförmige Bewegungen mit konstanter Beschleunigung¶
In gleicher Weise, wie eine Beschleunigung  eine Änderung der
Geschwindigkeit
eine Änderung der
Geschwindigkeit  eines Körpers hervorruft, bewirkt eine
Winkelbeschleunigung
eines Körpers hervorruft, bewirkt eine
Winkelbeschleunigung  eine Änderung der Winkelgeschwindigkeit
eine Änderung der Winkelgeschwindigkeit
 eines Körpers.
eines Körpers.
Zwischen der Winkelbeschleunigung  und der in der Zeit
und der in der Zeit
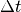 bewirkten Änderung der Winkelgeschwindigkeit
bewirkten Änderung der Winkelgeschwindigkeit 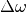 gilt folgender Zusammenhang:
gilt folgender Zusammenhang:
(4)¶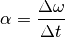
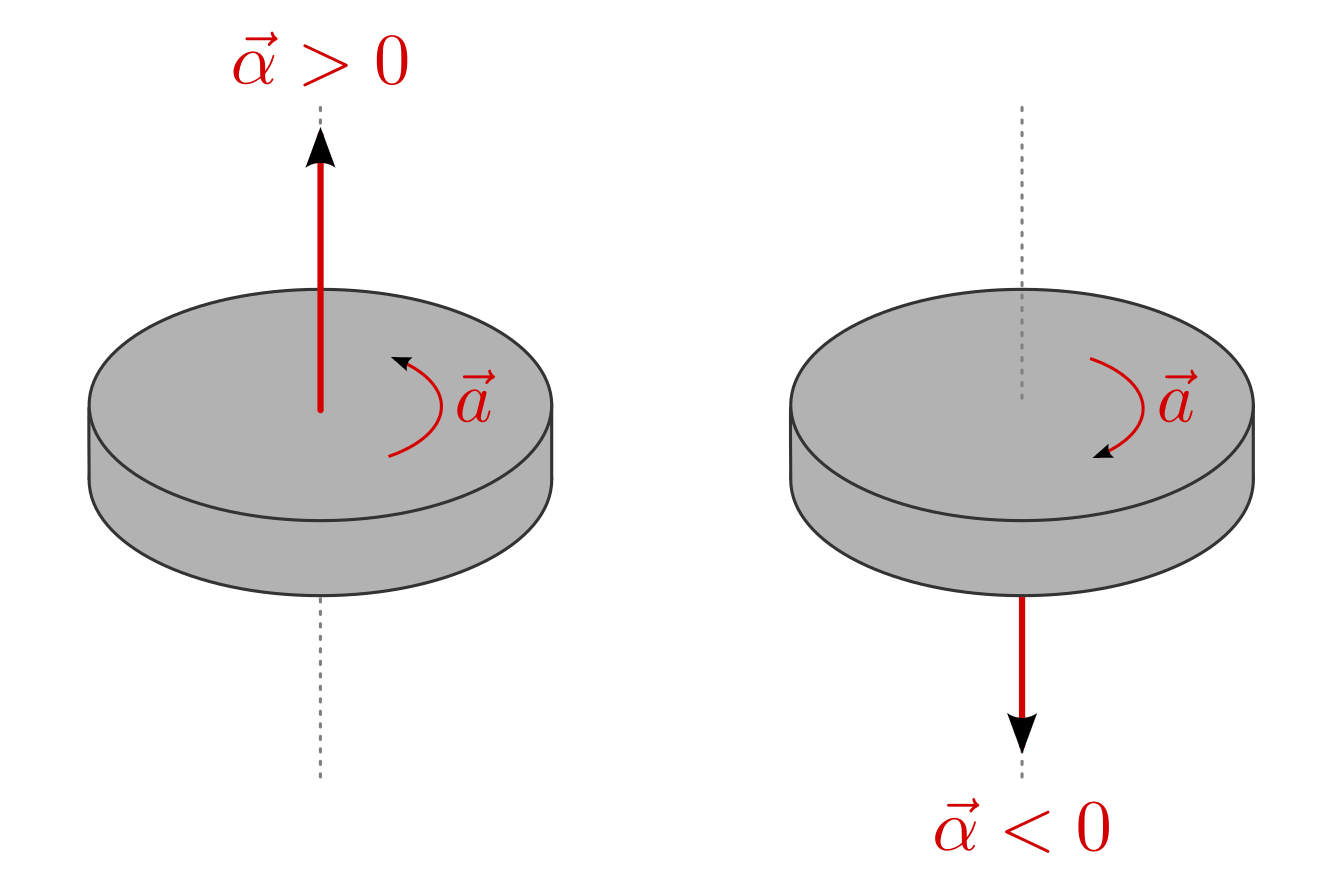
Die Winkelbeschleunigung ist, wie auch die Winkelgeschwindigkeit, eine vektorielle Größe. Wird beispielsweise eine liegende Scheibe gegen den Uhrzeigersinn beschleunigt, so zeigt die Winkelbeschleunigung nach oben, andernfalls nach unten.[2] Allgemein kann wiederum die „Rechten-Hand-Regel“ genutzt werden: Zeigen die Finger der rechten Hand in die Beschleunigungsrichtung, so zeigt der Daumen die Richtung der Winkelbeschleunigung an.
Da sich bei einer Bewegung auf einer Kreisbahn der Radius  nicht
ändert, gibt es einen weiteren Zusammenhang zwischen der Winkelbeschleunigung
und der gewöhnlichen tangentialen Beschleunigung
nicht
ändert, gibt es einen weiteren Zusammenhang zwischen der Winkelbeschleunigung
und der gewöhnlichen tangentialen Beschleunigung  :
:
(5)¶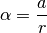
Für den während der beschleunigten Kreisbewegung durchlaufenen Drehwinkel
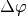 gilt ebenfalls in Analogie zur beschleunigten
geradlinigen Bewegung:
gilt ebenfalls in Analogie zur beschleunigten
geradlinigen Bewegung:
(6)¶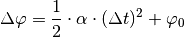
Hierbei gibt 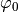 den anfänglichen Winkel der kreisförmigen
Bewegung an.
den anfänglichen Winkel der kreisförmigen
Bewegung an.
An einem rotierfähigen Gegenstand treten Winkelbeschleunigungen immer dann auf,
wenn ein resultierendes Drehmoment 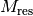 auf den Gegenstand einwirkt; für die Winkelbeschleunigung gilt dabei
auf den Gegenstand einwirkt; für die Winkelbeschleunigung gilt dabei
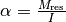 , wobei
, wobei  für das
Trägheitsmoment des Gegenstands steht.
für das
Trägheitsmoment des Gegenstands steht.
Anmerkungen:
| [1] | Die Indizes der Bahngeschwindigkeiten können somit weggelassen werden,
man kann also einfacher  für für 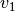 und und 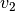 sowie sowie
 für für 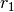 und und 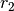 schreiben. schreiben. |
| [2] | Ebenso ist die Winkelbeschleunigung negativ, wenn ein sich mit positiver Winkelgeschwindigkeit (gegen den Uhrzeigersinn) bewegender Gegenstand auf der Kreisbahn abgebremst wird – er wird gleichermaßen in Gegenrichtung beschleunigt. |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

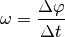
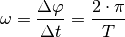
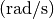 angegeben (
angegeben (![\unit[1]{rad} \approx
57,3 \degree](../../_images/math/40bf269e7274a0475c015a98e5204c3577847781.png) ).
).