Kinematik¶
Bewegungen mit konstanter Geschwindigkeit¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Bewegungen mit konstanter Geschwindigkeit.
Eindimensionale Bewegungen mit konstanter Geschwindigkeit
(*) Bei den folgenden Aufgaben geht es jeweils um durchschnittliche Geschwindigkeiten oder Bewegungsvorgänge mit konstanter Geschwindigkeit:
- Ein Läufer legt eine Strecke
![s = \unit[8,0]{km}](../../_images/math/548efce1bacf2da5abd8121732efbdad2f914b67.png) in einer Zeit von
in einer Zeit von
![t = \unit[30]{min}](../../_images/math/70611aebf660bfef505eae6e9369fca58e6cb5b7.png) zurück. Wie groß ist seine
Durchschnittsgeschwindigkeit
zurück. Wie groß ist seine
Durchschnittsgeschwindigkeit 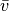 ?
? - Ein Radfahrer legt alle
![\Delta t=\unit[6,0]{s}](../../_images/math/fb336e4f716fa32023dee05bd71c2c0fce970ba2.png) eine Wegstrecke von
eine Wegstrecke von
![\Delta s=\unit[36]{m}](../../_images/math/9c6ec2a6ba7e6b94f5353173383e4c1154b0be24.png) zurück. Wie groß ist seine Geschwindigkeit?
zurück. Wie groß ist seine Geschwindigkeit? - Der Weltrekord im
![\unit[100]{m}](../../_images/math/7b66d4a05cc49b5789c12562bc7ebf8c77605e27.png) -Lauf aus dem Jahr 2009 liegt bei
-Lauf aus dem Jahr 2009 liegt bei
![t=\unit[9,58]{s}](../../_images/math/64bd7475b9fb27e43d67b06e68a62ab265d805fb.png) . Welche mittlere Geschwindigkeit
. Welche mittlere Geschwindigkeit 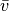 in
in
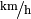 hatte der Läufer?
hatte der Läufer? - Welche Durchschnittsgeschwindigkeit erreicht ein Zug, der um 9:05 Uhr in
Augsburg abfährt und um 12:35 Uhr im
![\Delta s = \unit[245]{km}](../../_images/math/395621b12d8116bd2249da93c39cb9afc803f110.png) weit
entfernten Würzburg ankommt?
weit
entfernten Würzburg ankommt? - Ein Auto fährt mit
![v= \unitfrac[108]{km}{h}](../../_images/math/6feff4ca7f7c530d6d800fde313c6edab24dca06.png) auf einer Autobahn. Welche
Wegstrecke legt es in einer Sekunde, welche in einer Minute zurück?
auf einer Autobahn. Welche
Wegstrecke legt es in einer Sekunde, welche in einer Minute zurück? - Wie viel Sekunden braucht man, um mit einer Geschwindigkeit von
![v =
\unitfrac[5,0]{km}{h}](../../_images/math/ae09f5983bf8a3adc81e8758cb7a2dc8335efeea.png) eine Strecke von
eine Strecke von ![\unit[800]{m}](../../_images/math/1f8b208e0d741f40bdb059bc0576da46eb73fabb.png) zurückzulegen?
zurückzulegen? - Das Licht legt in einer Sekunde rund
![\unit[300\,000]{km}](../../_images/math/1f8e8af7ebfb7ac671aa251732b61da1373fb816.png) zurück. Die
Entfernung Erde-Sonne beträgt ungefähr
zurück. Die
Entfernung Erde-Sonne beträgt ungefähr ![s = \unit[150\,000\,000]{km}](../../_images/math/dd9c0f97ea3c1078cae58c84ff7318403a59855f.png) .
Welche Zeit benötigt das Licht von der Sonne zur Erde?
.
Welche Zeit benötigt das Licht von der Sonne zur Erde?
- Ein Läufer legt eine Strecke
(*) Die Schallgeschwindigkeit in Luft beträgt ca.
![v =
\unitfrac[330]{m}{s}](../../_images/math/4cd296d6243c21acabd496617f38668160ee7825.png) . Ein Wanderer steht gegenüber einer großen Felswand und
ruft laut „Haallooo!!“. Erst nach einer Zeit von
. Ein Wanderer steht gegenüber einer großen Felswand und
ruft laut „Haallooo!!“. Erst nach einer Zeit von ![t = \unit[5,0]{s}](../../_images/math/e85d955cfce9138668cd9f3dec384c3f16fe9df5.png) hört
er ein Echo. Wie weit ist die Felswand vom Wanderer entfernt?
hört
er ein Echo. Wie weit ist die Felswand vom Wanderer entfernt?
(*) Bewegung ist relativ. Konkret bedeutet das:
„Eine Bewegung ist die Änderung der Lage eines Körpers gegenüber einem anderen Körper. Wenn ein Körper seine Lage gegenüber einem anderen Körper nicht ändert, dann ist er in Ruhe gegenüber diesem Körper.“
Wie verhält sich dies bezüglich der Lage eines sitzenden Fahrgasts in einem sich bewegenden Schnellzug? Ist der Fahrgast in Ruhe, oder bewegt er sich?
(**) Bei einem „Verfolgungsrennen“ startet zunächst eine Gruppe an Läufern; nach einer Zeit von
![\Delta t = \unit[30]{min}](../../_images/math/8accc73d3fa97410227ccf35278277888b77870b.png) startet ein Fahrzeug am
Ausgangspunkt und fährt den Läufern mit einer konstanten Geschwindigkeit von
startet ein Fahrzeug am
Ausgangspunkt und fährt den Läufern mit einer konstanten Geschwindigkeit von
![v_{\mathrm{F}}=\unitfrac[35]{km}{h}](../../_images/math/07c8f79946863e68d67d33254f7475a0aef4920f.png) hinterher. Das Rennen ist für
jeden einzelnen Läufer beendet, sobald das Fahrzeug ihn eingeholt hat.
hinterher. Das Rennen ist für
jeden einzelnen Läufer beendet, sobald das Fahrzeug ihn eingeholt hat.Nach welcher Wegstrecke
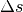 beziehungsweise welcher Zeit
beziehungsweise welcher Zeit
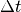 holt das Fahrzeug einen Läufer ein, dessen durchschnittliche
Geschwindigkeit
holt das Fahrzeug einen Läufer ein, dessen durchschnittliche
Geschwindigkeit ![v_{\mathrm{L}} = \unitfrac[15]{km}{h}](../../_images/math/0ed187de8ef5093a44ce16329b099b41da61717d.png) beträgt?
beträgt?
(**) Ein Fahrzeug startet mit einer Geschwindigkeit
![v_1 =
\unitfrac[30,0]{km}{h}](../../_images/math/58b024bb16ab38b4cbfee3629a0dd001670c6edd.png) von Ort
von Ort 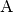 nach Ort
nach Ort
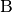 . Gleichzeitig startet von Ort
. Gleichzeitig startet von Ort 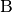 ein
Fahrzeug mit
ein
Fahrzeug mit ![v_2 = \unitfrac[50,0]{km}{h}](../../_images/math/e422357eea11b6339b494f92ea2d200e74dacab6.png) nach Ort
nach Ort 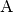 .
Die Strecke zwischen beiden Orten kann als geradlinig angenommen werden, ihre
Länge beträgt
.
Die Strecke zwischen beiden Orten kann als geradlinig angenommen werden, ihre
Länge beträgt ![s = \unit[100]{km}](../../_images/math/f0f47a4fc73a472bd089a6eb9b1947314c361e9f.png) . An welcher Stelle treffen sich die
beiden Fahrzeuge?
. An welcher Stelle treffen sich die
beiden Fahrzeuge?
Mehrdimensionale Bewegungen mit konstanter Geschwindigkeit
Die folgenden Aufgaben beziehen sich auf den Abschnitt Mehrdimensionale Bewegungen mit konstanter Geschwindigkeit.
(*) Ein Schwimmer bewegt sich mit
![v_y=\unitfrac[0,5]{m}{s}](../../_images/math/54cad9d122da2a638520d23c88ff823271109cd1.png) quer zur
Strömung eines Flusses. Er wird um
quer zur
Strömung eines Flusses. Er wird um ![s_x=\unit[35]{m}](../../_images/math/ff5c2f7cff433c40528feb130e6c4e45ceb1bd17.png) abgetrieben, bis
er das
abgetrieben, bis
er das ![s_y = \unit[100]{m}](../../_images/math/e3a64dbc9f8dc193f29859397d8cbb2e5ba097b8.png) entfernte Ufer erreicht. Wie groß ist die
(durchschnittliche) Strömungsgeschwindigkeit
entfernte Ufer erreicht. Wie groß ist die
(durchschnittliche) Strömungsgeschwindigkeit 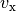 des Flusses?
des Flusses?
- (**) Zwei als punktförmig anzusehende Objekte, die sich zunächst am gleichen
Ort befinden, bewegen sich in einem Winkel von
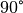 mit
mit
![v_1=\unit[5]{\frac{m}{s}}](../../_images/math/a9355566f735dd606d4d72566d458e74f7f54f22.png) und
und ![v_2=\unit[3]{\frac{m}{s}}](../../_images/math/0c2ca69cacc924b5ef6af3b052347dcfc9294552.png) auseinander. Mit welcher Relativgeschwindigkeit
auseinander. Mit welcher Relativgeschwindigkeit 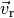 entfernen sich die beiden Objekte voneinander? Welche relative Ortsveränderung
ergibt sich nach
entfernen sich die beiden Objekte voneinander? Welche relative Ortsveränderung
ergibt sich nach ![t=\unit[15]{s}](../../_images/math/ac9ce3cc1e8358d3aa3d11594e485ca7174efa3d.png) , von einem der Punkte aus betrachtet?
, von einem der Punkte aus betrachtet?
Bewegungen mit konstanter Beschleunigung¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Bewegungen mit konstanter Beschleunigung.
Eindimensionale Bewegungen mit konstanter Beschleunigung
(*) Welche durchschnittliche Beschleunigung erreicht ein Radfahrer, der aus dem Stand (
![v_0 = \unitfrac[0]{m}{s}](../../_images/math/615ab627e0fd9c9cfcecd4e6d27ad948f7cad7da.png) ) in einer Zeit von
) in einer Zeit von ![t =
\unit[8,0]{s}](../../_images/math/98743ef13e580e7dd40b30bebf827f57e72a671d.png) eine Geschwindigkeit von
eine Geschwindigkeit von ![v = \unitfrac[30]{km}{h}](../../_images/math/b8119075a2fdf23a661b4769226b24ae843c4312.png) erreicht?
erreicht?
(*) Wie groß ist die Beschleunigung eines Fahrzeugs, das in
![\unit[10]{s}](../../_images/math/5ed0ad0ea613205263b3055e878ac643cfef28f3.png) von
von ![\unitfrac[0]{km}{h}](../../_images/math/8f097ca03046a58df8eb5738626867b9b87ffa5f.png) auf
auf ![\unitfrac[100]{km}{h}](../../_images/math/0bf686e35ff7c75c7fa800dacf3839195b0a66f7.png) beschleunigt? Welche Beschleunigung ergibt sich im umgekehrten Fall, wenn das
Fahrzeug in
beschleunigt? Welche Beschleunigung ergibt sich im umgekehrten Fall, wenn das
Fahrzeug in ![\unit[10]{s}](../../_images/math/5ed0ad0ea613205263b3055e878ac643cfef28f3.png) von
von ![\unitfrac[100]{km}{h}](../../_images/math/0bf686e35ff7c75c7fa800dacf3839195b0a66f7.png) auf
auf
![\unitfrac[0]{km}{h}](../../_images/math/8f097ca03046a58df8eb5738626867b9b87ffa5f.png) abbremst?
abbremst?
(*) Wie groß ist die Beschleunigung
 eines Fahrzeugs, das in
eines Fahrzeugs, das in
![\Delta t = \unit[5,0]{s}](../../_images/math/ad20d472c014c4fc50e8449ac8809424b4d416a9.png) von
von ![v_1 = \unitfrac[20,0]{m}{s}](../../_images/math/de9b5757448ffad7dbfdcb64bbe5c42e373d1867.png) auf
auf
![v_2 = \unitfrac[36,5]{m}{s}](../../_images/math/694080501cd1f0e080a8d7938e2efa446ecd6290.png) beschleunigt? Wie groß ist der
Beschleunigungswert im Vergleich zum Wert der Erdbeschleunigung
beschleunigt? Wie groß ist der
Beschleunigungswert im Vergleich zum Wert der Erdbeschleunigung ![(g =
\unitfrac[9,81]{m}{s^2})](../../_images/math/62792919ce1643a235de300d27d4d980c3f571a3.png) , und welche Wegstrecke legt das Fahrzeug während des
Beschleunigungsvorgangs zurück?
, und welche Wegstrecke legt das Fahrzeug während des
Beschleunigungsvorgangs zurück?
(**) Ein PKW fährt innerorts mit
![v_0 = \unitfrac[40]{km}{h}](../../_images/math/ccb823738dfdb2d9587d628cb991cc26312d9cda.png) .
Plötzlich bemerkt der Fahrer in
.
Plötzlich bemerkt der Fahrer in ![\Delta s = \unit[25]{m}](../../_images/math/64d3c0a281b6aef2c092714239867ab8dde23605.png) Entfernung ein
Hindernis. Nach einer Reaktionszeit von
Entfernung ein
Hindernis. Nach einer Reaktionszeit von ![\Delta t = \unit[1,0]{s}](../../_images/math/ae650455879aa09051dff820946763ffd1d0ac22.png) bremst er den Wagen mit einer Beschleunigung von
bremst er den Wagen mit einer Beschleunigung von
![a=\unitfrac[-4,5]{m}{s^2}](../../_images/math/1597aebf13cf1827ccc1a919fa7ab053c2914e9b.png) ab. Kommt der Wagen noch rechtzeitig vor dem
Hindernis zum Stillstand?
ab. Kommt der Wagen noch rechtzeitig vor dem
Hindernis zum Stillstand?
(**) Ein Badegast eines Schwimmbades springt aus einer Höhe von
![h=\unit[5,0]{m}](../../_images/math/28355a908b35b9d8860c9b9b0a8ad502260eed90.png) ins Wasser. Der Luftwiderstand kann hierbei
vernachlässigt werden, die Erdbeschleunigung beträgt
ins Wasser. Der Luftwiderstand kann hierbei
vernachlässigt werden, die Erdbeschleunigung beträgt ![g =
\unitfrac[9,81]{m}{s^2}](../../_images/math/03805fc8ebe3cf4d9756368930b8d3e2249f9c96.png) . Wie lange dauert seine Flugzeit, und welche
Geschwindigkeit hat er in dem Moment, in dem er ins Wasser eintaucht?
. Wie lange dauert seine Flugzeit, und welche
Geschwindigkeit hat er in dem Moment, in dem er ins Wasser eintaucht?
(**) Ein Stein, der in einen Brunnen fallen gelassen wird, erfährt durch die Erdanziehung eine Beschleunigung von
![(g = \unitfrac[9,81]{m}{s^2})](../../_images/math/ad520bfc5d0c91a85b623ad4d9ed5c6aece67412.png) .
Anfangs hat der Stein eine Geschwindigkeit von
.
Anfangs hat der Stein eine Geschwindigkeit von ![v_0 =
\unitfrac[0]{m}{s}](../../_images/math/5082fedae54b9e840e292071a1bff555561e74a1.png) ; nach einer Zeit von
; nach einer Zeit von ![t = \unit[1,7]{s}](../../_images/math/de5bc293a00736c020ed3d483d481d76f20ebb5a.png) kommt er
auf dem Grund des Brunnens auf. Welche Geschwindigkeit erreicht der Stein
dabei, wenn der Luftwiderstand vernachlässigt werden kann? Welche Strecke legt
er bis zum Aufprall zurück?
kommt er
auf dem Grund des Brunnens auf. Welche Geschwindigkeit erreicht der Stein
dabei, wenn der Luftwiderstand vernachlässigt werden kann? Welche Strecke legt
er bis zum Aufprall zurück?
(**) Wie groß ist die Beschleunigung, die ein Fahrer bei frontalem Aufprall eines Fahrzeugs gegen eine Mauer erfährt, wenn die Knautschzone
![\Delta
s = \unit[0,5]{m}](../../_images/math/1666cbb2565ad9d21389a8b1bfbabf423c7b9621.png) und die Aufprallgeschwindigkeit
und die Aufprallgeschwindigkeit ![v = \unitfrac[30]{km}{h}](../../_images/math/b8119075a2fdf23a661b4769226b24ae843c4312.png) beträgt?
Wie groß ist die Beschleunigung, wenn das Fahrzeug nicht gegen eine Wand
fährt, sondern frontal auf ein baugleiches und gleich schnell in die
Gegenrichtung fahrendes Fahrzeug trifft?
beträgt?
Wie groß ist die Beschleunigung, wenn das Fahrzeug nicht gegen eine Wand
fährt, sondern frontal auf ein baugleiches und gleich schnell in die
Gegenrichtung fahrendes Fahrzeug trifft?Wie groß ist die Beschleunigung, wenn die Aufprallgeschwindigkeit bei
![\unitfrac[50]{km}{h}](../../_images/math/0a3011f2f4f4e704bfdd66399afaf97d0336699c.png) oder
oder ![\unitfrac[100]{km}{h}](../../_images/math/0bf686e35ff7c75c7fa800dacf3839195b0a66f7.png) liegt?
liegt?
Kreisförmige Bewegungen¶
Die folgenden Aufgaben beziehen sich auf den Abschnitt Kreisförmige Bewegungen.
(*) Ein Stein wird an eine Schnur gebunden und im Kreis geschleudert; plötzlich reißt die Schnur. In welcher Richtung fliegt der Stein weiter? Um was für einen Bewegungstyp handelt es sich folglich bei einer kreisförmigen Bewegung?
(*) Ein Fahrradreifen mit einem Durchmesser von
![d=\unit[72]{cm}](../../_images/math/a303183a35519f3d80fd783604b70478893c3622.png) dreht
sich in einer Sekunde
dreht
sich in einer Sekunde 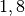 mal. Wie groß ist dabei die Umlaufzeit
mal. Wie groß ist dabei die Umlaufzeit
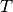 ? Welche Winkelgeschwindigkeit und welche Bahngeschwindigkeit hat ein
Kieselstein, der sich im Profil des Mantels festgesetzt hat?
? Welche Winkelgeschwindigkeit und welche Bahngeschwindigkeit hat ein
Kieselstein, der sich im Profil des Mantels festgesetzt hat?
(*) Ein PKW fährt mit einer Geschwindigkeit von
![\unitfrac[90]{km}{h}](../../_images/math/12289af701d172a51e0611788cdb59dbb81fd642.png) .
Wie groß sind die Winkelgeschwindigkeit
.
Wie groß sind die Winkelgeschwindigkeit  und die Drehzahl
und die Drehzahl
 der Räder, wenn deren Durchmesser
der Räder, wenn deren Durchmesser ![d=\unit[45]{cm}](../../_images/math/f3bcfbcbb7bdf9f70895c192a406f178730d3dab.png) beträgt?
beträgt?
(*) Wie groß ist die Radialbeschleunigung
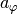 einer
Zentrifuge mit Radius
einer
Zentrifuge mit Radius ![r = \unit[1,00]{cm}](../../_images/math/66d73839d5ca5b380f92c539c3b5c0b1196e7e89.png) , wenn sie eine Drehzahl von
, wenn sie eine Drehzahl von
![n = \unitfrac[3\,000]{U}{min}](../../_images/math/34c6becd90e1d6cdcb4e6c0ac9c3288034aebfc4.png) aufweist?
aufweist?
(**) Welche Radialbeschleunigung
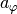 erfährt ein
Körper, der auf Höhe des Äquators mit der Erde (Radius
erfährt ein
Körper, der auf Höhe des Äquators mit der Erde (Radius ![r_{\mathrm{E}} =
\unit[6378]{km}](../../_images/math/de1f6794c28c60ec824046d3e34f4d4a6d8cb43c.png) ) mitrotiert? Wie groß ist
) mitrotiert? Wie groß ist 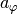 bei
einem Körper, der sich auf Höhe des 45. nördlichen Breitengrades bzw. am
Nordpol befindet?
bei
einem Körper, der sich auf Höhe des 45. nördlichen Breitengrades bzw. am
Nordpol befindet?
