Bewegungen mit konstanter Geschwindigkeit¶
Im folgenden Abschnitt werden zunächst anhand von eindimensionalen Bewegungen einige grundlegende Konzepte zur mathematischen Beschreibung von Bewegungsvorgängen vorgestellt; diese werden dann auf zwei- beziehungsweise dreidimensionale Vorgänge übertragen.
Eindimensionale Bewegungen mit konstanter Geschwindigkeit¶
Eine geradlinige Bewegung stellt die einfachste Variante eines Bewegungsvorgangs
dar: Es genügt bereits eine einzelne Raumachse als Koordinatensystem. Hat man
(willkürlich, aber verbindlich) den Nullpunkt sowie die Richtung der
Koordinatenachse einmalig festgelegt, so genügt folglich eine einzige
Längenangabe  , um den Ort des Objekts bezüglich des
Koordinatenursprungs exakt angeben zu können:
, um den Ort des Objekts bezüglich des
Koordinatenursprungs exakt angeben zu können:
- Hat der Ort
 einen positiven Wert, so befindet sich das Objekt um den
entsprechenden Wert entlang der als positiv gewählten Raumrichtung vom
Koordinatenursprung entfernt.
einen positiven Wert, so befindet sich das Objekt um den
entsprechenden Wert entlang der als positiv gewählten Raumrichtung vom
Koordinatenursprung entfernt. - Hat der Ort
 einen negativen Wert, so befindet sich das Objekt um den
entsprechenden Wert entgegen der als positiv gewählten Raumrichtung vom
Koordinatenursprung entfernt.
einen negativen Wert, so befindet sich das Objekt um den
entsprechenden Wert entgegen der als positiv gewählten Raumrichtung vom
Koordinatenursprung entfernt.
Bei Bewegungsvorgängen ändert sich der Ort  des Objekts im zeitlichen
Verlauf; man schreibt daher häufig auch explizit
des Objekts im zeitlichen
Verlauf; man schreibt daher häufig auch explizit 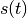 , um die
Abhängigkeit des Orts
, um die
Abhängigkeit des Orts  von der Zeit
von der Zeit  auszudrücken.
auszudrücken.
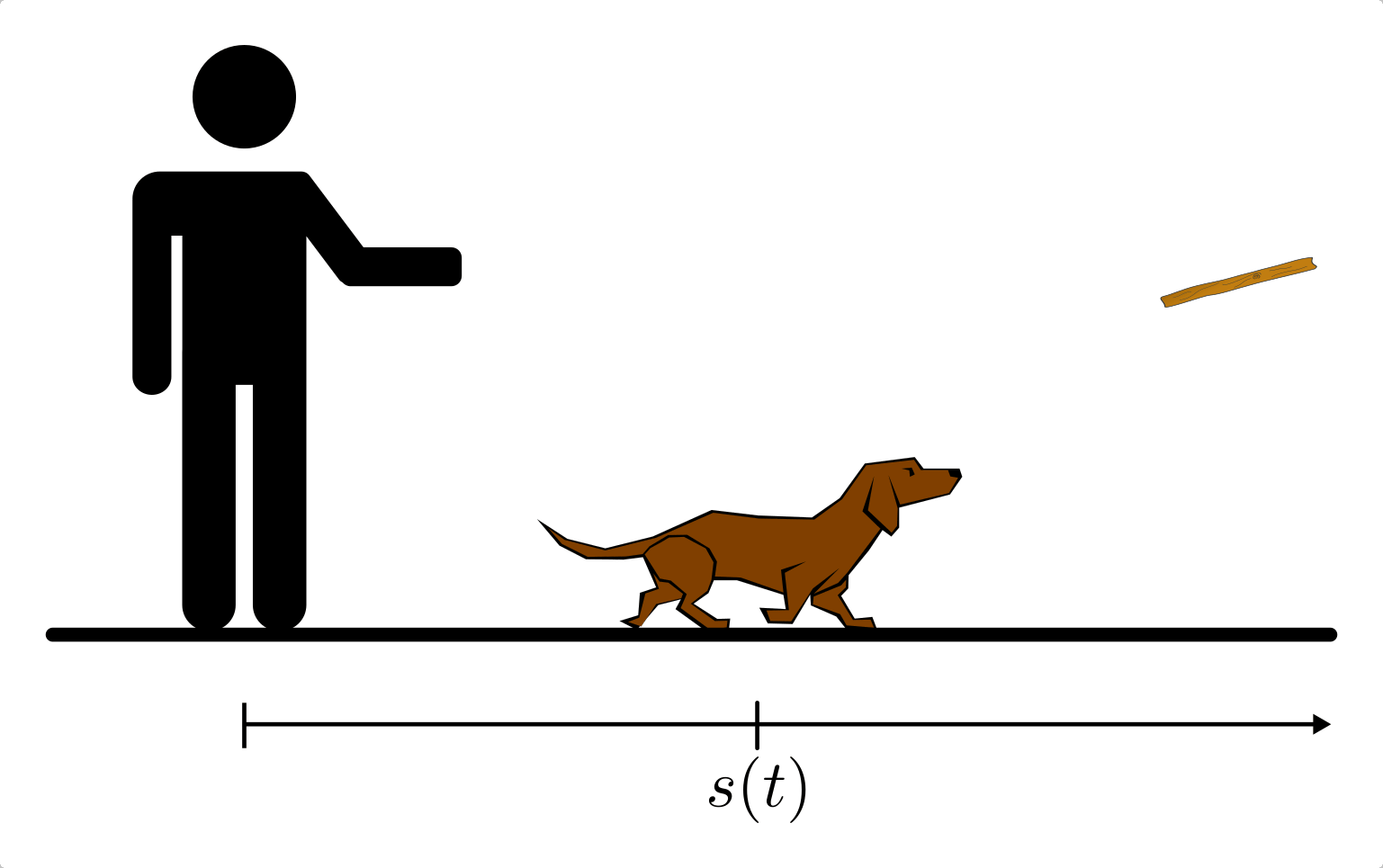
Die Bewegung eines Hundes, der einem Stöckchen nacheilt oder es zurückbringt, kann in guter Näherung als geradlinige Bewegung aufgefasst werden.
Die  -Schreibweise
-Schreibweise
Das Symbol  wird nicht nur für Ortsangaben verwendet, sondern ebenfalls
um zurückgelegte Wegstrecken anzugeben. In diesem Fall wählt man allerdings
bevorzugt die Schreibweise
wird nicht nur für Ortsangaben verwendet, sondern ebenfalls
um zurückgelegte Wegstrecken anzugeben. In diesem Fall wählt man allerdings
bevorzugt die Schreibweise 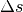 , um Verwechslungen zu vermeiden. Das
, um Verwechslungen zu vermeiden. Das
 -Symbol (ein griechisches „Delta“) steht dabei für „Differenz“ –
gemeint ist damit, inwiefern sich der Wert von
-Symbol (ein griechisches „Delta“) steht dabei für „Differenz“ –
gemeint ist damit, inwiefern sich der Wert von  am Ende
des Bewegungsvorgangs von dem Wert
am Ende
des Bewegungsvorgangs von dem Wert  zu Beginn des
Bewegungsvorgangs unterscheidet:
zu Beginn des
Bewegungsvorgangs unterscheidet:
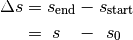
Dass bei dieser Konvention der Startwert (meist mit 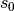 bezeichnet) vom
Endwert (meist mit
bezeichnet) vom
Endwert (meist mit  bezeichnet) abgezogen wird, hat folgenden Grund:
bezeichnet) abgezogen wird, hat folgenden Grund:
- Ist der Anfangswert
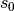 kleiner als der Endwert
kleiner als der Endwert  , so verläuft
die Bewegung entlang der als positiv definierten Bewegungsrichtung.
, so verläuft
die Bewegung entlang der als positiv definierten Bewegungsrichtung. - Ist umgekehrt der Endwert
 kleiner als der Anfangswert
kleiner als der Anfangswert 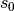 ,
so verläuft die Bewegung in Richtung der negativen Koordinatenachse.
,
so verläuft die Bewegung in Richtung der negativen Koordinatenachse.
Gilt für den Startwert 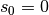 , so beginnt die Bewegung am Nullpunkt des
Koordinatensystems, und für den Zeitpunkt
, so beginnt die Bewegung am Nullpunkt des
Koordinatensystems, und für den Zeitpunkt  gilt
gilt 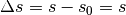 . In diesem Fall stimmt somit zu einem Zeitpunkt
. In diesem Fall stimmt somit zu einem Zeitpunkt  der Ort
der Ort
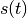 mit der zurückgelegten Wegstrecke
mit der zurückgelegten Wegstrecke 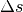 überein, und das
überein, und das
 kann weggelassen werden; im Allgemeinen ist dies jedoch nicht der
Fall.
kann weggelassen werden; im Allgemeinen ist dies jedoch nicht der
Fall.
Die gleiche  -Schreibweise wird auch für einzelne Zeitabschnitte
verwendet; auch hier gilt beispielsweise
-Schreibweise wird auch für einzelne Zeitabschnitte
verwendet; auch hier gilt beispielsweise 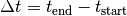 . Diese Schreibweise hat den Vorteil, dass man einen Vorgang
in verschiedenen Zeitabschnitten
. Diese Schreibweise hat den Vorteil, dass man einen Vorgang
in verschiedenen Zeitabschnitten 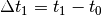 ,
, 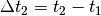 , usw. unterteilen kann, sofern in diesen beispielsweise
unterschiedliche Geschwindigkeiten oder Bewegungsrichtungen vorliegen; eine
komplexe Aufgabenstellung kann so in mehrere einfacher zu lösende Teile zerlegt
werden.
, usw. unterteilen kann, sofern in diesen beispielsweise
unterschiedliche Geschwindigkeiten oder Bewegungsrichtungen vorliegen; eine
komplexe Aufgabenstellung kann so in mehrere einfacher zu lösende Teile zerlegt
werden.
Definition von Geschwindigkeit
Bewegt sich ein Objekt mit konstanter Geschwindigkeit, so legt es in gleichen Zeitabschnitten die jeweils gleiche Wegstrecke zurück.
Definition:
Die Geschwindigkeit
eines sich mit konstanter Geschwindigkeit bewegenden Objekts ist gleich dem Verhältnis aus der zurückgelegten Wegstrecke
und der dazu benötigten Zeit
:
(1)¶
Einheit:
Die Geschwindigkeit wird meist in Kilometer je Stunde () oder in Meter je Sekunde (
) angegeben.
Beispiele:
- Licht legt in einer Sekunde
![\unit[300\,000]{km}](../../_images/math/1f8e8af7ebfb7ac671aa251732b61da1373fb816.png) zurück. Die
Lichtgeschwindigkeit beträgt somit
zurück. Die
Lichtgeschwindigkeit beträgt somit ![\unitfrac[300\,000\,000]{m}{s}](../../_images/math/2afe979e6fe26b83a80b20e44030276b04c96ed6.png) .
. - Eine Schnecke legt in einer Sekunde etwa
![\unit[0,8]{mm}](../../_images/math/c680179612a388109e7584458d8857b855e752c3.png) zurück.
„Schneckentempo“ entspricht somit ungefähr
zurück.
„Schneckentempo“ entspricht somit ungefähr ![\unitfrac[0,0008]{m}{s}](../../_images/math/9e355ea82f2bf4c35b2a3d952f431646efb750c9.png) .
.
Umrechnung von km/h in m/s
Sowohl 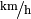 als auch
als auch 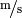 sind als
Geschwindigkeits-Einheiten üblich. Um sie ineinander umzurechnen, kann man
folgende Zusammenhänge nutzen:
sind als
Geschwindigkeits-Einheiten üblich. Um sie ineinander umzurechnen, kann man
folgende Zusammenhänge nutzen:
![\unit[1]{km} &= \unit[1000]{m} \\
\unit[1]{h} = \unit[60]{min} &= \unit[60 \cdot 60]{s} = \unit[3600]{s}](../../_images/math/35253dcfcf4c81b9417a08adb7e35b23eb1cea35.png)
Daraus folgt:
![\unit[1]{\frac{km}{h}} = \frac{\unit[1]{km}}{\unit[1]{h}} =
\frac{\unit[1000]{m}}{\unit[3600]{s}} = \unit[\frac{1000}{3600}
]{\frac{m}{s} } = \unit[\frac{1}{3,6} ]{\frac{m}{s} }](../../_images/math/b699841f271ecb83dccb17af9a7b9d817eb4e3c8.png)
und umgekehrt:
(2)¶![\unit[1]{\frac{m}{s} } = \unit[3,6]{\frac{km}{h} }](../../_images/math/38697c18b56d7eb8690da93b10b1d101ce347085.png)
Ein Spaziergänger beispielsweise, der sich mit knapp ![\unitfrac[5]{km}{h}](../../_images/math/dc3004f290f4e2894ba86168d130b49545230416.png) bewegt, legt also in einer Sekunde etwas mehr als einen Meter zurück.
bewegt, legt also in einer Sekunde etwas mehr als einen Meter zurück.
Ort und zurückgelegte Wegstrecke
Der zeitliche Verlauf der Geschwindigkeit kann allgemein in Form eines
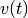 -Diagramms darstellt werden. Hierbei wird der Betrag der
Geschwindigkeit in Abhängigkeit von der Zeit wie der Graph einer mathematischen
Funktion in ein zweidimensionales
Koordinatensystem eingezeichnet.
-Diagramms darstellt werden. Hierbei wird der Betrag der
Geschwindigkeit in Abhängigkeit von der Zeit wie der Graph einer mathematischen
Funktion in ein zweidimensionales
Koordinatensystem eingezeichnet.
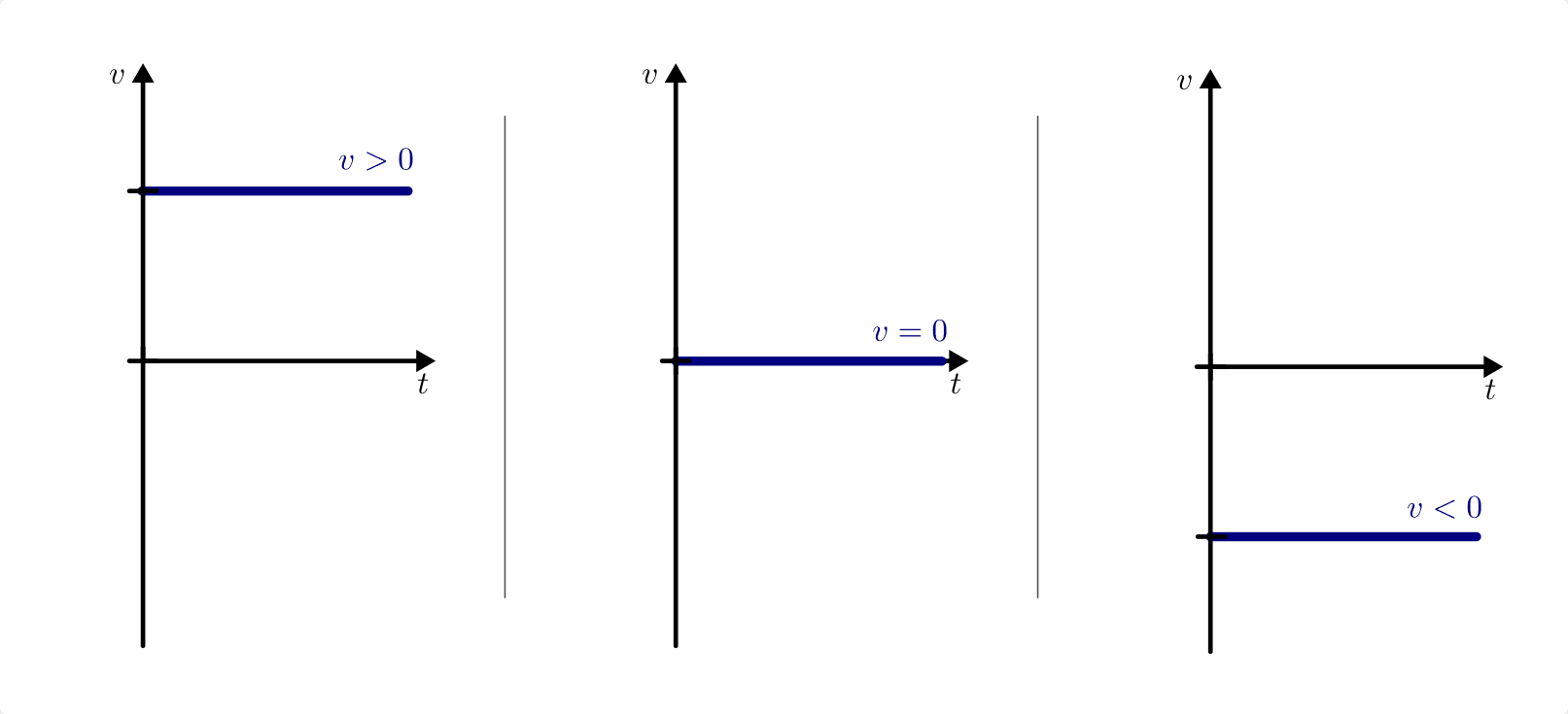
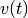 -Diagramme einer konstanten Geschwindigkeit. Der Wert der
Geschwindigkeit kann größer, gleich oder kleiner Null sein.
-Diagramme einer konstanten Geschwindigkeit. Der Wert der
Geschwindigkeit kann größer, gleich oder kleiner Null sein.
Im Fall einer zeitlich konstanten Geschwindigkeit entspricht der Graph der
Geschwindigkeit einer waagrechten Geraden. Der Wert der
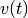 -Geraden hat folgende Bedeutung:
-Geraden hat folgende Bedeutung:
- Umso größer der Wert der Geschwindigkeit ist, desto weiter ist die
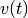 -Gerade von der horizontalen
-Gerade von der horizontalen  -Achse (entspricht dem Wert
-Achse (entspricht dem Wert
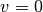 ) entfernt.
) entfernt. - „Ruhe“ ist der Spezialfall einer Bewegung mit konstanter Geschwindigkeit, für
den gerade
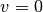 gilt.
gilt. - Bewegt sich ein Objekt in die entgegengesetzt zur ursprünglich als „positiv“ festgelegten Richtung, so erhält seine Geschwindigkeit ein negatives Vorzeichen.
Kennt man die (konstante) Geschwindigkeit  eines Objekts und weiß, wie
lange es mit dieser Geschwindigkeit unterwegs ist, so kennt man allerdings noch
nicht den genauen Ort, an dem sich das Objekt zur Zeit
eines Objekts und weiß, wie
lange es mit dieser Geschwindigkeit unterwegs ist, so kennt man allerdings noch
nicht den genauen Ort, an dem sich das Objekt zur Zeit  befindet. Man
weiß nämlich nicht, von welchem Startpunkt aus die Bewegung begonnen hat. Um den
Ort
befindet. Man
weiß nämlich nicht, von welchem Startpunkt aus die Bewegung begonnen hat. Um den
Ort 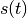 des Objekts in Abhängigkeit von der Zeit angeben zu können,
muss also die Startposition
des Objekts in Abhängigkeit von der Zeit angeben zu können,
muss also die Startposition 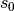 mit berücksichtigt werden:
mit berücksichtigt werden:
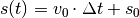
Der zeitliche Verlauf der zurückgelegten Wegstrecke kann ebenfalls graphisch in
Form eines so genannten Weg-Zeit-Diagramms („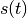 -Diagramm“) dargestellt
werden. Aus Gleichung (1) folgt, dass sich die Wegstrecke
-Diagramm“) dargestellt
werden. Aus Gleichung (1) folgt, dass sich die Wegstrecke
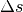 bei konstanter Geschwindigkeit
bei konstanter Geschwindigkeit  in gleichen
Zeitabschnitten
in gleichen
Zeitabschnitten 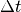 kontinuierlich um
kontinuierlich um 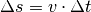 ändert – die entsprechende Weg-Zeit-Linie entspricht also einer
Geraden.
ändert – die entsprechende Weg-Zeit-Linie entspricht also einer
Geraden.
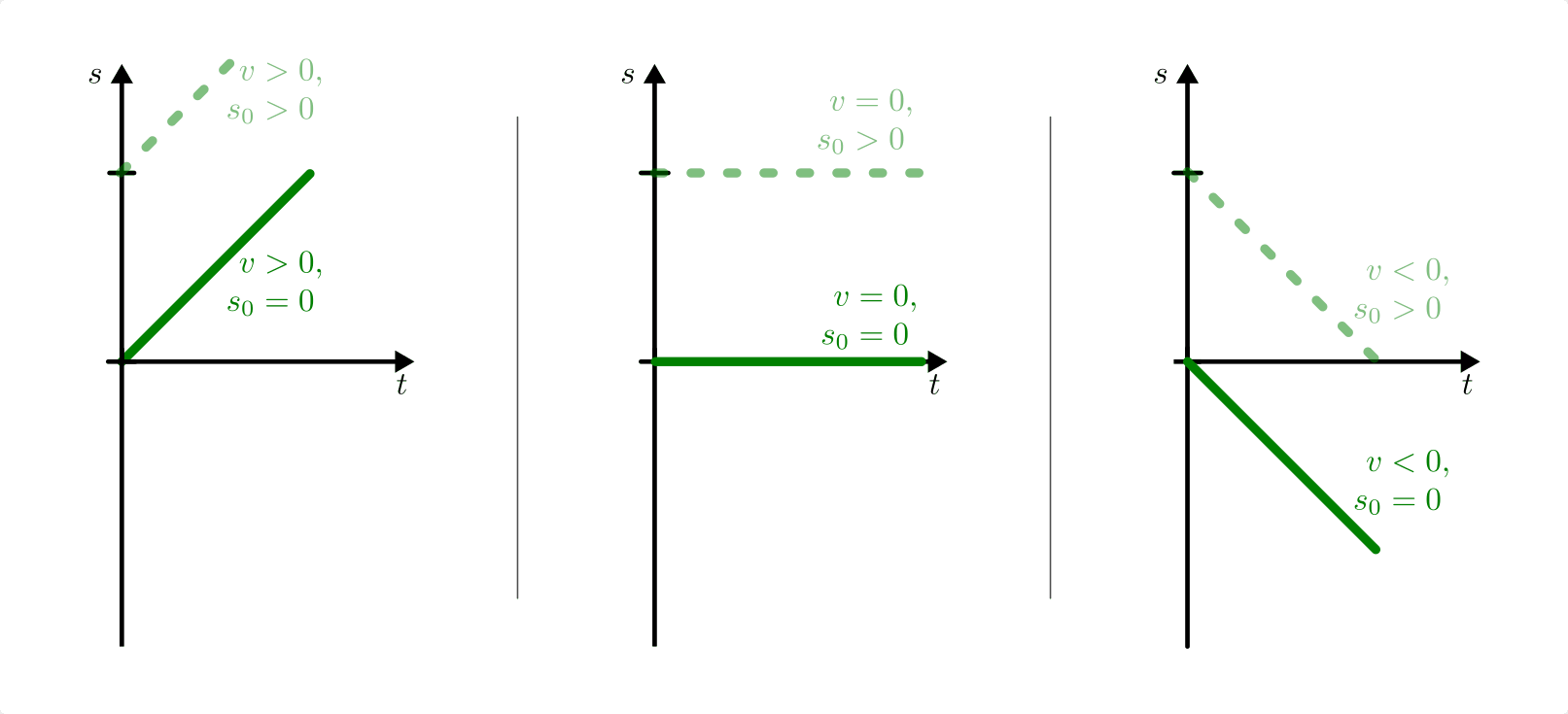
 -Diagramme einer konstanten Geschwindigkeit. Die Steigung der
Weg-Zeit-Geraden kann größer, gleich oder kleiner Null sein.
-Diagramme einer konstanten Geschwindigkeit. Die Steigung der
Weg-Zeit-Geraden kann größer, gleich oder kleiner Null sein.
Die Steigung der Geraden in
einem 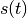 -Diagramm hat folgende Bedeutung:
-Diagramm hat folgende Bedeutung:
- Umso größer die (konstante) Geschwindigkeit ist, desto steiler ist der Verlauf
der Geraden im
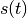 -Diagramm.
-Diagramm. - Ist die Geschwindigkeit eines Objekts konstant gleich Null, so bleibt seine
Entfernung vom Beobachter unverändert – egal, ob sich das beobachtete Objekt
an der Position des Beobachters oder in einer Entfernung
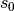 vom Beobachter entfernt liegt. In beiden Fällen entspricht zeitliche Verlauf
des zurückgelegten Weges einer waagrechten Geraden.
vom Beobachter entfernt liegt. In beiden Fällen entspricht zeitliche Verlauf
des zurückgelegten Weges einer waagrechten Geraden. - Das Vorzeichen der Geschwindigkeit gibt an, ob die Gerade im
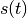 -Diagramm steigt oder fällt. Eine negative Steigung bedeutet
hierbei, dass sich das beobachtete Objekt entgegen der ursprünglich als
„positiv“ festgelegten Raumrichtung bewegt – egal, ob die Bewegung vom
Beobachter oder von einer um die Strecke
-Diagramm steigt oder fällt. Eine negative Steigung bedeutet
hierbei, dass sich das beobachtete Objekt entgegen der ursprünglich als
„positiv“ festgelegten Raumrichtung bewegt – egal, ob die Bewegung vom
Beobachter oder von einer um die Strecke 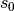 entfernten
Stelle aus beginnt.
entfernten
Stelle aus beginnt.
Der Wert, den die Ortsfunktion 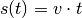 zu einer bestimmten Zeit
zu einer bestimmten Zeit
 annimmt, entspricht jeweils der Fläche zwischen der entsprechen
Geschwindigkeits-Zeit-Linie und der
annimmt, entspricht jeweils der Fläche zwischen der entsprechen
Geschwindigkeits-Zeit-Linie und der  -Achse im
-Achse im 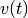 -Diagramm;
gegebenenfalls muss das Vorzeichen berücksichtigt werden und die anfängliche
Entfernung
-Diagramm;
gegebenenfalls muss das Vorzeichen berücksichtigt werden und die anfängliche
Entfernung 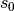 zum Ergebnis hinzu addiert werden.
zum Ergebnis hinzu addiert werden.
Die Durchschnittsgeschwindigkeit
Auch wenn sich die Geschwindigkeit mit der Zeit beziehungsweise entlang einer Wegstrecke mehrfach ändert, so kann man trotzdem für den gesamten Bewegungsvorgang eine durchschnittliche Geschwindigkeit angeben.
Definition:
Die Durchschnittsgeschwindigkeiteines Objekts ist gleich dem Verhältnis aus der Wegstrecke
, die er insgesamt zurücklegt, und der dazu benötigten Zeit
:
(3)¶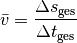
Beispiel:
- Ein Radrennfahrer legt eine Etappe von
![\unit[130]{km}](../../_images/math/4ab686b37443e5f7f4367403b8c462782672163c.png) in einer Zeit
von
in einer Zeit
von ![\unit[4,0]{h}](../../_images/math/22cc9c9f51262c49c634b1cc8dc680e4eee3dc36.png) zurück. Seine Durchschnittsgeschwindigkeit beträgt
somit:
zurück. Seine Durchschnittsgeschwindigkeit beträgt
somit:
![\bar{v} = \frac{\Delta s_{\mathrm{ges}}}{\Delta t_{\mathrm{ges}}} =
\frac{\unit[130]{km}}{\unit[4]{h}} = \unit[32,5]{\frac{km}{h}}](../../_images/math/2d46f34f1c77a8739b44568ff38927db030d2516.png)
Man sieht, dass auch bei diesem Vorgang das Modell der geradlinigen Bewegung verwendet werden kann, auch wenn sich der Radfahrer sehr wahrscheinlich nicht geradlinig fortbewegt. Bei vielerlei Fragestellungen ist allerdings nicht der konkrete Streckenverlauf von Bedeutung, sondern nur die Länge der Strecke. Kennt man zusätzlich die durchschnittliche Geschwindigkeit, so weiß man, wie lange der Bewegungsvorgang dauern wird; derartige Abschätzungen sind beispielsweise bei Wanderungen oder Fahrrad-Touren durchaus hilfreich.
Die Relativgeschwindigkeit
Bewegen sich zwei Objekte von einem gleichen Ausgangspunkt aus mit verschiedenen
Geschwindigkeiten 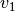 und
und 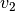 in die gleiche Richtung, so
entspricht ihre gegenseitige Entfernung der Differenz der zurückgelegten
Wegstrecken; die Objekte entfernen sich also mit zunehmender Zeit voneinander.
Die wachsende Entfernung kann durch die so genannte Relativgeschwindigkeit
in die gleiche Richtung, so
entspricht ihre gegenseitige Entfernung der Differenz der zurückgelegten
Wegstrecken; die Objekte entfernen sich also mit zunehmender Zeit voneinander.
Die wachsende Entfernung kann durch die so genannte Relativgeschwindigkeit
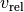 ausgedrückt werden:
ausgedrückt werden:
(4)¶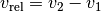
Diese Gleichung gibt die Relativgeschwindigkeit des zweiten Objekts relativ zum
ersten Objekt an; umgekehrt gibt 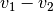 die Geschwindigkeit des
ersten Objekts relativ zum zweiten an. Beide Relativgeschwindigkeiten haben den
gleichen Betrag, ein unterschiedliches Vorzeichen, da sie in ihren Richtungen
entgegengesetzt sind.
die Geschwindigkeit des
ersten Objekts relativ zum zweiten an. Beide Relativgeschwindigkeiten haben den
gleichen Betrag, ein unterschiedliches Vorzeichen, da sie in ihren Richtungen
entgegengesetzt sind.
Das Rechnen mit Relativgeschwindigkeiten ist beispielsweise hilfreich, um die für Überholvorgänge mit konstanten Geschwindigkeiten notwendigen Zeiten beziehungsweise Wegstrecken zu berechnen. Zudem können, wie im folgenden Abschnitt gezeigt wird, mittels Relativgeschwindigkeiten auch Entfernungen zwischen Objekten berechnet werden, die sich mit konstanten Geschwindkeiten in unterschiedlichen Raumrichtungen bewegen.
Mehrdimensionale Bewegungen mit konstanter Geschwindigkeit¶
Die im letzten Abschnitt vorgestellten Gesetzmäßigkeiten für eindimensionale
Bewegungen lassen sich auch ohne großen Aufwand auf zweidimensionale Bewegungen
übertragen. Ein Grundprinzip hierbei ist, dass jeder zweidimensionale
Bewegungsvorgang in eine 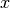 - und eine
- und eine 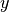 -Komponente aufgeteilt
werden kann. Die Ausrichtung des Koordinatensystems kann wiederum einmalig frei
gewählt werden kann, ist für den Rest der Rechnung dann allerdings verbindlich.
-Komponente aufgeteilt
werden kann. Die Ausrichtung des Koordinatensystems kann wiederum einmalig frei
gewählt werden kann, ist für den Rest der Rechnung dann allerdings verbindlich.
Ein zweites Grundprinzip ist, dass einzelne Bewegungsvorgänge, auch wenn sie entlang unterschiedlicher Raumrichtungen stattfinden, jeweils getrennt voneinander betrachtet werden können.
Addition von Teilgeschwindigkeiten
Verlaufen zwei Bewegungen geradlinig entlang einer gemeinsamen Linie, so genügt
eine einfache Addition der beiden Geschwindigkeitsbeträge 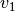 und
und
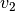 , um die resultierende Geschwindigkeit zu erhalten.
, um die resultierende Geschwindigkeit zu erhalten.
Beispiele:
Eine Person bewegt sich mit einer Geschwindigkeit
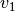 auf einem
Laufband entgegen der Laufbandgeschwindigkeit
auf einem
Laufband entgegen der Laufbandgeschwindigkeit 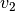 . Sind beide
Geschwindigkeiten gleich groß, so bleibt die Person an der gleichen Stelle –
die resultierende Geschwindigkeit
. Sind beide
Geschwindigkeiten gleich groß, so bleibt die Person an der gleichen Stelle –
die resultierende Geschwindigkeit  ist gleich Null.
ist gleich Null.Sind beide Geschwindigkeiten unterschiedlich groß, so bewegt sich die Person in Richtung der größeren Geschwindigkeit.[1]
Stimmt die Bewegungsrichtung der Person mit der Richtung der Laufbandgeschwindigkeit überein, so addieren sich die Beträge beider Geschwindigkeiten. Die Geschwindigkeit
 der Person (relativ zum
Erdboden) ist somit gleich
der Person (relativ zum
Erdboden) ist somit gleich 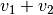 .
.
Die Addition der auftretenden Geschwindigkeiten ist auch möglich, wenn diese in
einem beliebigen Winkel zueinander stehen. Zeichnerisch stellt man dazu die
beiden Geschwindigkeiten 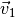 und
und 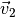 als Pfeile dar, deren Richtungen mit denen der beiden Geschwindigkeiten
übereinstimmen und deren Längen die Beträge beider Geschwindigkeiten abbilden.
Nach den Regeln der Vektor-Addition lässt sich damit aus beiden Geschwindigkeits-Pfeilen die Richtung und
der Betrag der resultierenden Geschwindigkeit
als Pfeile dar, deren Richtungen mit denen der beiden Geschwindigkeiten
übereinstimmen und deren Längen die Beträge beider Geschwindigkeiten abbilden.
Nach den Regeln der Vektor-Addition lässt sich damit aus beiden Geschwindigkeits-Pfeilen die Richtung und
der Betrag der resultierenden Geschwindigkeit 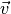 graphisch
ermitteln.
graphisch
ermitteln.
Betrag und Richtung der resultierenden Geschwindigkeit 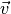 können
auch rechnerisch bestimmt werden. Für eine zweidimensionale Bewegung (in einer
Ebene) gilt:
können
auch rechnerisch bestimmt werden. Für eine zweidimensionale Bewegung (in einer
Ebene) gilt:
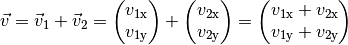
Die resultierende Geschwindigkeit 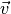 entspricht somit einer
komponentenweisen Addition der beiden Geschwindigkeits-Vektoren
entspricht somit einer
komponentenweisen Addition der beiden Geschwindigkeits-Vektoren
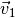 und
und 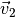 . Für den Betrag der
resultierenden Geschwindigkeit
. Für den Betrag der
resultierenden Geschwindigkeit 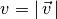 gilt:
gilt:
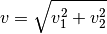
Aus dem Verhältnis der 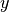 - zur
- zur 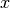 -Komponente lässt sich der
Winkel der resultierenden Geschwindigkeit bestimmen:
-Komponente lässt sich der
Winkel der resultierenden Geschwindigkeit bestimmen:
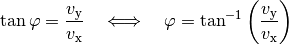
Beispiel:
Ein Boot überquert mit einer Geschwindigkeit
![v_1 =
\unit[3]{\frac{m}{s}}](../../_images/math/e32b823ff7167833fd1e54ed8b50af53e5101003.png) senkrecht einen Fluss, der mit einer Geschwindigkeit
senkrecht einen Fluss, der mit einer Geschwindigkeit
![v_2 = \unit[1]{\frac{m}{s}}](../../_images/math/4939dbbf13b6b1cf3e4d1db5424f5665e5492c55.png) strömt. Legt man ein Koordinatensystem so
an, dass die
strömt. Legt man ein Koordinatensystem so
an, dass die 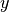 -Achse in Richtung der Geschwindigkeit des Bootes und
die
-Achse in Richtung der Geschwindigkeit des Bootes und
die 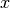 -Achse in Richtung der Flussströmung zeigt, so folgt für die
resultierende Geschwindigkeit
-Achse in Richtung der Flussströmung zeigt, so folgt für die
resultierende Geschwindigkeit 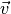 :
: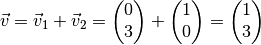
Der Betrag der resultierenden Geschwindigkeit ist hierbei:
![v = \sqrt{v_1^2 + v_2^2} = \sqrt{\left(\unit[1]{\frac{m}{s}}\right)^2 +
\left( \unit[3]{\frac{m}{s}}\right)^2} = \sqrt{\unit[10]{\frac{m^2}{s^2}}}
\approx \unit[3,16]{\frac{m}{s}}](../../_images/math/436b35c8c04611e9b560f5214e7bf38c97374654.png)
Der Winkel gegenüber der
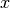 -Achse (Richtung des Flusses) beträgt:
-Achse (Richtung des Flusses) beträgt: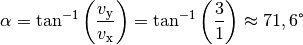
Das Boot driftet somit um einem Winkel von rund
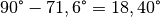 ab.
ab.
Die in die jeweiligen Richtungen zurückgelegten Wegstrecken 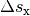 und
und 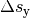 lassen sich wiederum
komponentenweise über die Formel
lassen sich wiederum
komponentenweise über die Formel 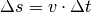 berechnen.
berechnen.
Eine weitere Verallgemeinerung auf dreidimensionale Bewegungsvorgänge erfolgt
nach den gleichen Prinzipien, indem man zusätzlich eine  -Komponente
betrachtet und folglich mit drei- anstelle mit zweidimensionalen Vektoren
rechnet.
-Komponente
betrachtet und folglich mit drei- anstelle mit zweidimensionalen Vektoren
rechnet.
Anmerkungen:
| [1] | Definiert man die Bewegungsrichtung der Person (nach rechts) als positiv,
so kann der Betrag der resultierenden Geschwindigkeit als Differenz beider
Geschwindigkeiten Schreibt man die Differenz |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

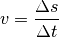
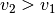 , so ist die resultierende Geschwindigkeit „negativ“, sie verläuft
somit von rechts nach links.
, so ist die resultierende Geschwindigkeit „negativ“, sie verläuft
somit von rechts nach links.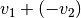 , so zeigt sich, dass auch in diesem Fall – unter Berücksichtigung
der Bewegungsrichtungen – die resultierende Geschwindigkeit gleich der
Summe der Einzelgeschwindigkeiten ist.
, so zeigt sich, dass auch in diesem Fall – unter Berücksichtigung
der Bewegungsrichtungen – die resultierende Geschwindigkeit gleich der
Summe der Einzelgeschwindigkeiten ist.