Raumkurve und Massenpunkt¶
Eine Bewegung entspricht einer Ortsveränderung eines Objekts relativ zu einem anderen, als ruhend angenommenen Objekt beziehungsweise Standpunkt – dieser entspricht normalerweise dem Ort des Beobachters.
Die Raumkurve
Je nach der Form der Bewegung (beispielsweise geradlinig, kreisförmig, innerhalb einer Ebene oder räumlich) wird zur physikalischen Beschreibung der Bewegung ein geeignetes Koordinatensystem („Bezugsystem“) gewählt. Im Ursprung des Koordinatensystems steht meistens der als ruhend angenommene Beobachter. Das beobachtete Objekt durchläuft bezüglich dieses Zentrums eine ein-, zwei- oder dreidimensionale Raumkurve („Trajektorie“).

Mögliche Raumkurven einer zweidimensionalen Bewegung von  nach
nach
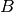 aus der Vogelperspektive: Geradlinig (1), kreisförmig (2) und
krummlinig (3).
aus der Vogelperspektive: Geradlinig (1), kreisförmig (2) und
krummlinig (3).
Der Massenpunkt
In vielen Fällen ist die physikalische Beschreibung einer Bewegung einfacher, wenn man sich das beobachtete Objekt als einen einzelnen Punkt im Koordinatensystem vorstellt. Dieser „Massenpunkt“ wird dabei so behandelt, als ob er die gesamte Masse des Objekts besäße – meist wird daher der Schwerpunkt des Objekts als Massenpunkt ausgewählt.[1]

Bei GPS-Geräten gilt der Beobachter als der „ruhende“ Bezugspunkt – aus dieser Perspektive bewegt sich die Welt an ihm vorbei.
Neben der Verschiebung des Schwerpunkts („Translation“) kann auch eine Drehung („Rotation“) des Objekts um dieses Zentrum stattfinden. Tritt eine Kombination beider Bewegungsformen auf, so können diese unabhängig voneinander betrachtet und die jeweiligen Effekte addiert werden; man spricht in diesem Fall von einer „Überlagerung“ von Bewegungsvorgängen. In den folgenden Abschnitten werden die zur Beschreibung von allgemeinen Bewegungsvorgängen nötigen Formeln und Überlegungen vorgestellt, wobei zunächst von einfachen Modellen ausgegangen wird und diese dann schrittweise erweitert werden.
Anmerkungen:
| [1] | In der Kinematik werden die zur Bewegung beziehungsweise Beschleunigung eines Objekts nötigen Kräfte nicht weiter betrachtet, sondern nur die Bewegung des Objekts selbst. Die Berücksichtigung der wirkenden Kräfte ist Aufgabe der so genannten Dynamik, welche auf der Kinematik aufbaut. |
